Hierarchisches Clustering: Konzeptübersicht mit Beispielen

Du wurdest gerade mit der Analyse eines großen Datensatzes beauftragt und sollst eine tiefgreifende Clusteranalyse erstellen. Du kennst den Begriff "hierarchisches Clustering", aber was ist das genau und wie funktioniert es? 

In diesem Artikel erläutern wir das Konzept des hierarchischen Clusterns und geben Beispiele aus der Praxis, damit du seine Anwendungen besser verstehst.

Was ist Hierarchisches Clustering?

Hierarchisches Clustering ist ein unüberwachtes Lernen Algorithmus, der verwendet wird, um ähnliche Datenpunkte in Clustern zu gruppieren. Es baut eine mehrstufige Hierarchie von Clustern auf, indem es entweder kleinere Cluster zu größeren zusammenfasst (agglomerativ) oder einen großen Cluster in kleinere aufteilt (divisiv). So entsteht eine baumartige Struktur, die als Dendrogramm bezeichnet wird.

Ein Dendrogramm ist eine visuelle Darstellung, die die Anordnung von Clustern und ihre Beziehungen zueinander veranschaulicht. Die Höhe der Äste in einem Dendrogramm stellt den Abstand oder die Unähnlichkeit dar, bei dem die Cluster zusammenkommen. Geringere Höhen weisen auf Cluster hin, die in geringerem Abstand zueinander stehen und somit eine größere Ähnlichkeit aufweisen.

Warum hierarchisches Clustering beim maschinellen Lernen wichtig ist

Hierarchisches Clustering ist besonders nützlich, wenn die Anzahl der Cluster nicht im Voraus bekannt ist. Es ermöglicht Datenanalysten und Datenwissenschaftlern die Struktur der Daten durch Dendrogramme visuell zu erkunden.

Diese Technik ist auch in der Lage, verschachtelte Cluster aufzudecken und wird häufig in Bereichen wie Genomik, Kundensegmentierung und Dokumentenorganisation eingesetzt.

Nehmen wir zum Beispiel an, wir haben einen Datensatz mit Kaufdatensätzen von Kunden. Mit hierarchischem Clustering können wir Kunden mit ähnlichem Kaufverhalten in Clustern zusammenfassen und potenzielle Marktsegmente für gezielte Marketingstrategien identifizieren.

Hierarchisches vs. K-Means Clustering

Wenn es darum geht, Aufgaben zu clustern, sind die meisten unentschlossen, was zwei Hauptmethoden angeht: Hierarchisches Clustering oder K-means Clustering.

Aber was macht sie anders? Schauen wir uns die Unterschiede an, um ein besseres Bild zu bekommen.

• K-Means:
• Vor der Ausführung muss die Anzahl der Cluster festgelegt werden.
• Effizient und skalierbar für große Datenmengen.
• Es wird angenommen, dass die Cluster kugelförmig und gleich groß sind.
• Hierarchisches Clustering:
• Erfordert keine vordefinierte Anzahl von Clustern.
• Durch die Dendrogramme ist die Interpretation einfacher.
• Langsamer bei großen Datensätzen, aber besser für die Erforschung von Strukturen.

Beim Vergleich der beiden Verfahren gibt es einige Bereiche, in denen das hierarchische Clustering eine herausragende Option ist.

Hier sind einige Bereiche, in denen hierarchisches Clustering gut ist:

• Flexibilität bei der Auswahl von Clustern mithilfe von Dendrogrammen.
• Gut für kleine Datensätze oder wenn eine visuelle Hierarchie benötigt wird.
• Bearbeitet komplexe Clusterformen.

Allerdings kann es auch einige Nachteile haben, wie zum Beispiel:

• Rechenaufwendig
• Empfindlich gegenüber verrauschten Daten und Ausreißern.

Du könntest fragen: Wann sollte ich hierarchisches Clustering verwenden?

Hierarchisches Clustering eignet sich hervorragend für die folgenden Anwendungen:

• Explorative Datenanalyse
• Analyse der Genexpressionsmuster
• Marktsegmentierung mit mittelgroßen Datensätzen

Arten des hierarchischen Clusterns

Bei der Technik des hierarchischen Clusterns erwarten dich verschiedene Arten, die jeweils unterschiedliche Erkenntnisse und Ergebnisse liefern. Die beiden Haupttypen der hierarchischen Clusterung sind die agglomerative (bottom-up) und die divisive (top-down) Clusterung.

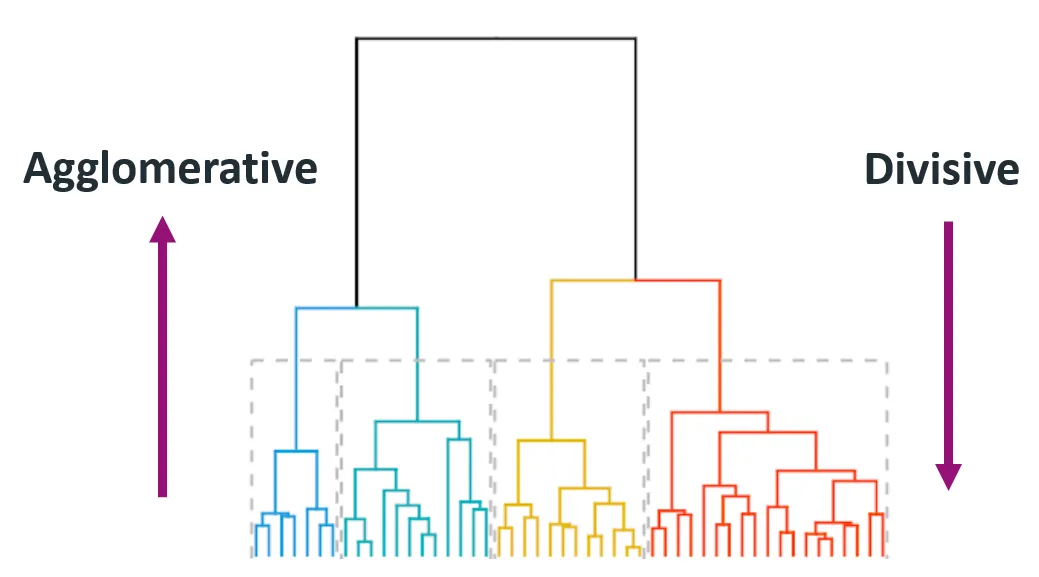
Quelle: Himanshu Sharma auf Medium

1. Agglomerativ (Bottom-Up)

Das agglomerative Clustering beginnt mit jedem Datenpunkt als einzelnem Cluster und fügt iterativ das nächstgelegene Paar von Clustern zusammen, bis nur noch ein Cluster übrig bleibt oder bis eine Haltebedingung erfüllt ist (z. B. eine gewünschte Anzahl von Clustern).

Diese Methode wird auch Bottom-up genannt, weil sie von unten (einzelne Datenpunkte) ausgeht und sich bis zur Spitze (endgültiger Cluster) aufbaut.

Schritt-für-Schritt-Anleitung:

1. Behandle jeden Datenpunkt als ein einzelnes Cluster.
2. Berechne die paarweisen Abstände zwischen allen Clustern.
3. Verschmelze die beiden Cluster mit dem geringsten Abstand.
4. Aktualisiere die Distanzmatrix, um die neue Gruppe von Clustern zu berücksichtigen.
5. Wiederhole die Schritte 2-4, bis alle Punkte zu einem einzigen Cluster gehören.

Diese Methode ist aufgrund ihrer Einfachheit und leichten Umsetzbarkeit weit verbreitet.

Hier ist ein Beispiel dafür, wie das in Python umgesetzt werden kann:

import numpy as np
from scipy.cluster.hierarchy import linkage, dendrogram, fcluster
import matplotlib.pyplot as plt

# Samples data
data = np.array([[1, 2], [2, 3], [5, 8], [8, 8], [1, 0], [0, 1]])

# Applies agglomerative clustering using Ward's method
Z = linkage(data, method='ward')

# Plots dendrogram
plt.figure(figsize=(8, 4))
dendrogram(Z)
plt.title('Agglomerative Clustering Dendrogram')
plt.xlabel('Data Points')
plt.ylabel('Distance')
plt.show()

# Extracts clusters (e.g., form 2 clusters)
clusters = fcluster(Z, t=2, criterion='maxclust')
print("Cluster assignments:", clusters)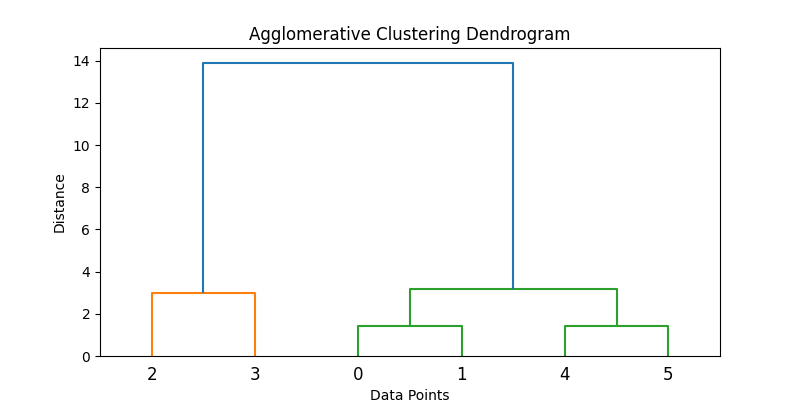

2. Divisiv (Top-Down)

Das Divisive Clustering beginnt mit allen Datenpunkten in einem einzigen Cluster und teilt sie rekursiv in kleinere Cluster auf. Der Prozess wird so lange fortgesetzt, bis sich jeder Datenpunkt in seinem eigenen Cluster befindet.

Er wird auch als Top-Down-Ansatz bezeichnet, da er an der Spitze beginnt (einzelner Cluster) und diesen in kleinere Cluster aufteilt.

Schritt-für-Schritt-Anleitung:

1. Beginne mit einem großen Cluster, der alle Datenpunkte enthält.
2. Teile die Gruppe in zwei möglichst unterschiedliche Gruppen auf.
3. Wende das Splitting-Verfahren rekursiv auf jeden entstandenen Cluster an.

Divisive Methoden sind aufgrund ihrer rekursiven Natur in der Regel rechenintensiver, und die Genauigkeit hängt stark von der Aufteilungsstrategie ab. Agglomerative Methoden sind aufgrund der einfachen Implementierung und der weit verbreiteten Softwareunterstützung weiter verbreitet.

Hinweis: Divisives hierarchisches Clustering wird in den Standard-Python-Bibliotheken nicht so leicht unterstützt wie agglomeratives Clustering. Ein Ansatz besteht darin, Clustering-Algorithmen wie k-means rekursiv anzuwenden.

Hier ist ein Codekonzept für ein simuliertes rekursives k-means-Splitting:

from sklearn.cluster import KMeans

def divisive_clustering(data, depth=2):
    if depth == 0 or len(data) <= 1:
        return [data]

    kmeans = KMeans(n_clusters=2, random_state=42).fit(data)
    labels = kmeans.labels_
    cluster1 = data[labels == 0]
    cluster2 = data[labels == 1]

    return divisive_clustering(cluster1, depth - 1) + divisive_clustering(cluster2, depth - 1)

# Run recursive splitting to simulate divisive clustering
split_clusters = divisive_clustering(data, depth=2)
for i, cluster in enumerate(split_clusters):
    print(f"Cluster {i+1} size: {len(cluster)}")

Dieser vereinfachte Code veranschaulicht einen konzeptionellen Ansatz für das divisive Clustering mit rekursivem K-means. Beachte jedoch, dass Standardaufteilungsmethoden wie DIANA andere Aufteilungskriterien verwenden.

Wichtige Konzepte und Terminologien

Hierarchisches Clustering beinhaltet einige Schlüsselkonzepte und Terminologien, die wichtig zu verstehen sind. Um den Prozess vollständig zu verstehen, gehen wir im Folgenden näher auf diese Konzepte ein.

1. Dendrogramme

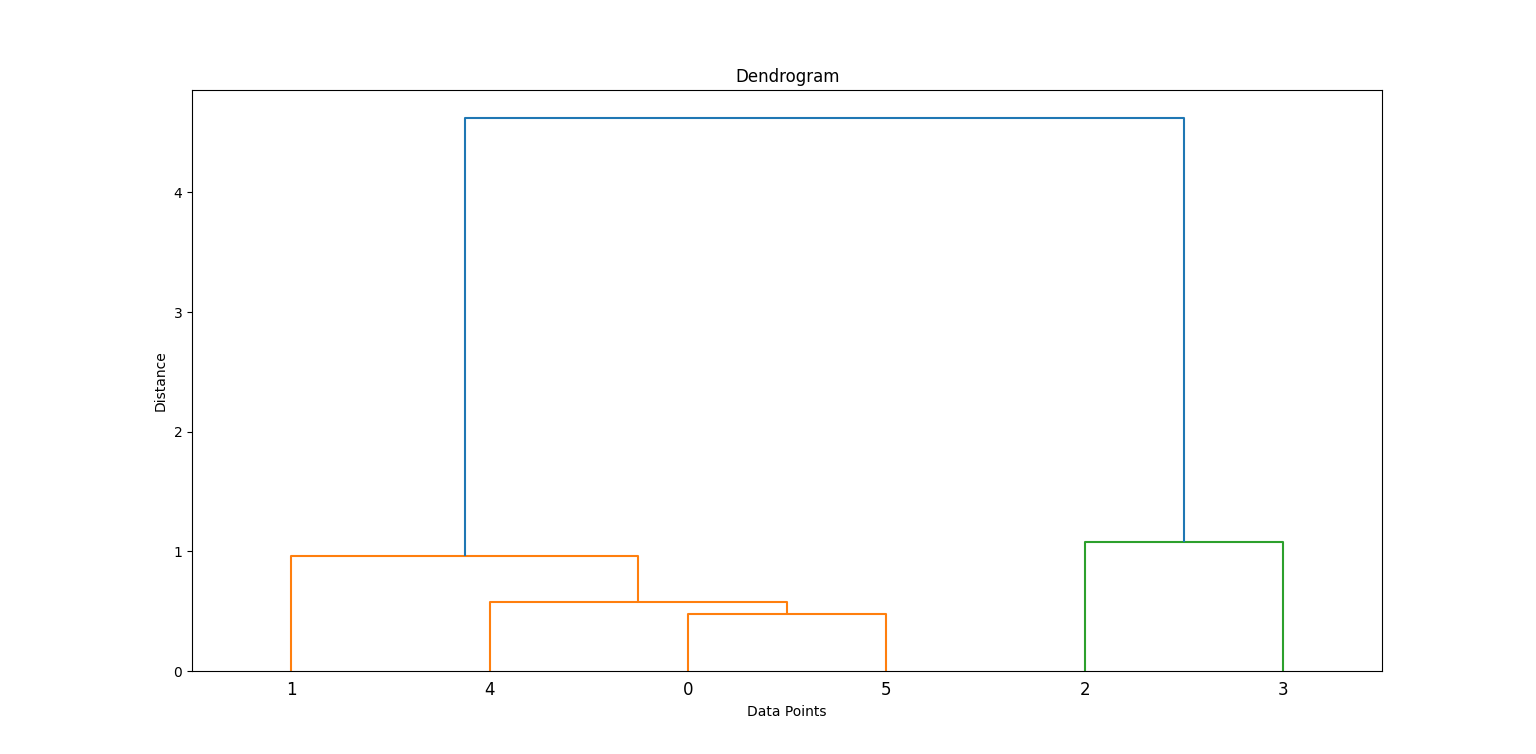
Ein Dendrogramm ist eine baumartige Struktur, die den Prozess des hierarchischen Clusterns visualisiert. Jede Ebene des Baums steht für eine Merge- oder Split-Operation, und die Höhe der Äste gibt den Abstand (oder die Unähnlichkeit) an, bei dem die Cluster zusammengeführt wurden.

Hier ist, warum das wichtig ist:

• Ermöglicht die visuelle Inspektion von Clustern auf verschiedenen Ebenen.
• Indem du das Dendrogramm auf einer bestimmten Höhe "schneidest", kannst du die Anzahl der Cluster wählen, die am besten zu den Daten passt.

2. Verknüpfungskriterien

Die Verknüpfungskriterien bestimmen, wie die Abstände zwischen den Clustern während des Zusammenführungsprozesses berechnet werden.

Hier sind einige Arten von Verknüpfungskriterien:

Einfaches Gestänge (Minimum)

Dieses Kriterium betrachtet den Abstand zwischen den nächstgelegenen Punkten von zwei Clustern. Das kann zu länglichen, kettenartigen Clustern führen.

from scipy.spatial.distance import pdist, squareform
data = np.array([[1, 2], [2, 3], [5, 8]])
distance_matrix = squareform(pdist(data, metric='euclidean')) 
single_linkage_min = np.min(distance_matrix[0, 1:])
print("Single Linkage Distance between Cluster A (point 1) and Cluster B (point 2, 3):", single_linkage_min)

Vollständige Verknüpfung (Maximum)

Bei diesem Kriterium geht es um den Abstand zwischen den am weitesten entfernten Punkten zweier Cluster. Dies führt zu kompakten, gleichmäßig großen Trauben.

single_linkage_max = np.max(distance_matrix[0, 1:])
print("Complete Linkage Distance between Cluster A and B:", single_linkage_max)

Durchschnittliche Verknüpfung (Mittelwert)

Bei diesem Kriterium geht es um den durchschnittlichen Abstand zwischen allen Punkten in einem Cluster und allen Punkten in einem anderen Cluster. So entsteht ein Gleichgewicht zwischen einfacher und vollständiger Verknüpfung.

average_linkage = np.mean(distance_matrix[0, 1:])
print("Average Linkage Distance between Cluster A and B:", average_linkage)

Diese vereinfachten Beispiele veranschaulichen, wie Entfernungen zunächst berechnet werden. Beim Clustering wenden diese Kriterien (einfache, vollständige, durchschnittliche Verknüpfung) jedoch iterativ Abstände zwischen ganzen Clustern an, nicht nur zwischen einzelnen Punkten.

Ward's Methode

Die Ward-Methode ist eine Abwandlung des Average Linkage-Ansatzes, der die Summe der quadratischen Differenzen innerhalb aller Cluster minimiert. Im Vergleich zu anderen Methoden führt sie tendenziell zu gleichmäßigeren Clustern. Außerdem entstehen dabei oft gut getrennte, kugelförmige Cluster.

from scipy.cluster.hierarchy import linkage
linkage_ward = linkage(data, method='ward')
print("Ward's Linkage Matrix:\n", linkage_ward)

Jede Methode hat ihre eigenen Stärken und sollte auf der Grundlage der Daten und des Anwendungsfalls ausgewählt werden.

3. Entfernungsmetriken

Die verwendete Distanzmetrik beeinflusst das Clustering-Ergebnis erheblich.

Euklidischer Abstand

Die Euklidische Entfernung ist der geradlinige Abstand zwischen zwei Punkten im mehrdimensionalen Raum. Sie ist die am häufigsten verwendete Distanzmetrik, insbesondere für geometrisch verteilte Daten.

Manhattan Entfernung

Die Manhattan-Distanz( ), auch bekannt als Taxidistanz oder L1-Distanz, ist die Summe der absoluten Unterschiede zwischen den Dimensionen. Es ist nützlich für gitterartige Daten wie Stadtteile oder Finanztransaktionen.

Kosinus-Ähnlichkeit

Kosinus-Ähnlichkeit misst den Kosinus des Winkels zwischen zwei Vektoren, die nicht Null sind. Diese Metrik ist ideal für Textdaten oder wenn die Größe keine Rolle spielt (z. B. bei Worthäufigkeitsvektoren).

Hierarchisches Clustering in Python implementieren

In diesem Abschnitt gehen wir durch eine praktische Implementierung des agglomerativen hierarchischen Clusterns mit Python. Wir behandeln alles von der Datenvorverarbeitung bis zur Visualisierung der Ergebnisse mithilfe eines Dendrogramms.

Bibliotheken

Wir beginnen damit, die notwendigen Bibliotheken zu importieren:

import numpy as np
import pandas as pd
from scipy.cluster.hierarchy import dendrogram, linkage, fcluster
from sklearn.preprocessing import StandardScaler
import matplotlib.pyplot as plt

Hier ist, was wir im obigen Code importiert haben:

• numpy und pandas für Datenmanipulationen
• scipy.cluster.hierarchy für Clustering und Dendrogrammerstellung
• sklearn.preprocessing.StandardScaler für die Merkmalsskalierung
• matplotlib für die Visualisierung

Beispielhafte Daten

Bevor wir mit unserer Analyse beginnen, erstellen wir einen Spielzeugdatensatz mit 2D-Punkten und skalieren ihn. Die Skalierung ist entscheidend für distanzbasierte Algorithmen.

So würde unser Beispieldatensatz aussehen.

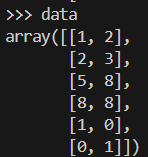
data = np.array([[1, 2], [2, 3], [5, 8], [8, 8], [1, 0], [0, 1]])
scaler = StandardScaler()
data_scaled = scaler.fit_transform(data)

Hier siehst du, wie das Datenfeld aussieht, nachdem es skaliert worden ist.

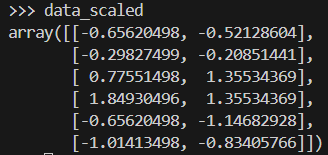
Erzeugen einer Verknüpfungsmatrix und eines Dendrogramms

Wir wenden die Ward-Methode an, um eine Verknüpfungsmatrix zu erstellen, die hierarchische Clustering-Informationen enthält. Dann zeichnen wir ein Dendrogramm.

linkage_matrix = linkage(data_scaled, method='ward')
plt.figure(figsize=(8, 4))
dendrogram(linkage_matrix)
plt.title('Dendrogram')
plt.xlabel('Data Points')
plt.ylabel('Distance')
plt.show()

Im obigen Code erstellt linkage die Cluster-Hierarchie und dendrogram hilft bei der Visualisierung, wie die Cluster gebildet wurden.

Indem wir untersuchen, wo die vertikalen Linien vor einer Zusammenführung am längsten sind, können wir entscheiden, wo wir "schneiden", um Cluster zu bilden. Suche nach der höchsten vertikalen Linie, die sich nicht mit anderen Clustern überschneidet. An dieser Stelle musst du den Schnitt machen.

In diesem Fall musst du bei 2 Clustern schneiden.

Erstellen von Clustern

Als Nächstes schneiden wir das Dendrogramm, um eine bestimmte Anzahl von Clustern mit fcluster zu erhalten:

clusters = fcluster(linkage_matrix, t=2, criterion='maxclust')
print(clusters)

plt.scatter(data_scaled[:, 0], data_scaled[:, 1], c=clusters, cmap='rainbow')
plt.title('Clusters')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.show()

Dadurch wird jeder Datenpunkt einem von zwei Clustern zugewiesen.

Einige zusätzliche Informationen über den Code:

• t=2: Gibt die gewünschte Anzahl von Clustern an.
• criterion='maxclust': Stellt sicher, dass wir genau t clusters erhalten.

Du kannst t ändern, um mit einer anderen Anzahl von Clustern zu experimentieren.

Praktisches Beispiel: Kundensegmentierung

Hierarchisches Clustering wird typischerweise bei der Kundensegmentierung eingesetzt. Mal sehen, wie das in der praktischen Umsetzung aussieht.

1. Datensatz-Übersicht

Lass uns einen Datensatz simulieren, der Kunden mit zwei Merkmalen darstellt: Alter und Einkommen. Wir werden make_blobs verwenden, um diese synthetischen Daten zu erzeugen.

from sklearn.datasets import make_blobs
X, _ = make_blobs(n_samples=100, centers=3, n_features=2, random_state=42)

2. Vorverarbeitung

Als Nächstes müssen wir die Merkmale standardisieren, um die Skalen zu normalisieren und die Genauigkeit des Clusterns zu verbessern.

scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)

Hier siehst du, wie die skalierten Daten aussehen:

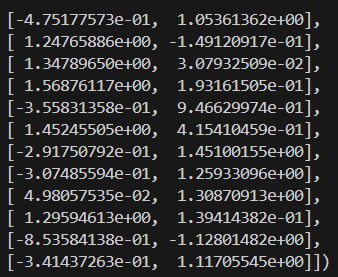
3. Anwendung des hierarchischen Clustering

Nachdem wir unsere Daten verarbeitet haben, stellen wir das Dendrogramm dar, um die Bildung von Clustern zu visualisieren.

linkage_matrix = linkage(X_scaled, method='ward')
plt.figure(figsize=(10, 5))
dendrogram(linkage_matrix)
plt.title('Customer Dendrogram')
plt.xlabel('Sample Index')
plt.ylabel('Distance')
plt.show()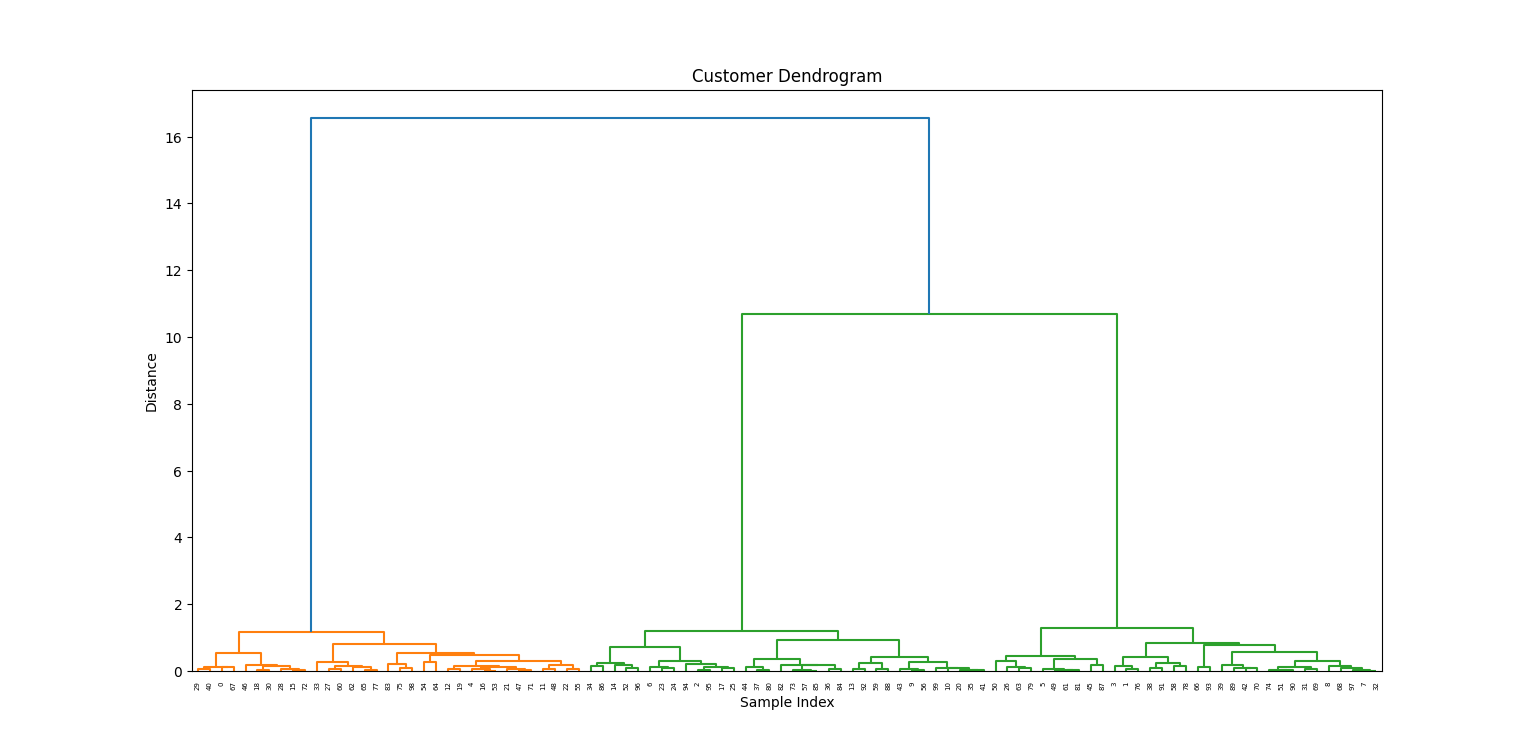

4. Ergebnisse interpretieren

Aus dem Dendrogramm wählen wir eine Höhe zum "Schneiden" und erstellen drei Cluster:

labels = fcluster(linkage_matrix, t=3, criterion='maxclust')
plt.scatter(X_scaled[:, 0], X_scaled[:, 1], c=labels, cmap='rainbow')
plt.title('Customer Segments')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.show()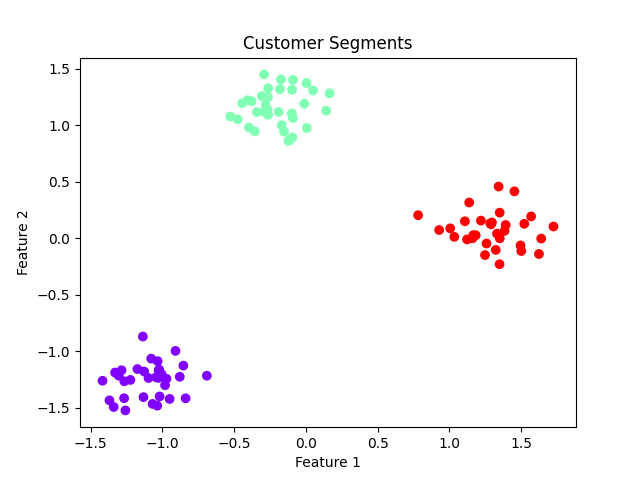

Auswirkungen auf das Geschäft:

• Die Cluster könnten Kundengruppen wie preisbewusste, mittlere und Premium-Kunden repräsentieren.
• Ermöglicht personalisiertes Marketing und verbesserte Kundenbeziehungsstrategien.

Hierarchisches Clustering Vorteile und Grenzen

Die Wahl des hierarchischen Clustering für deine Analyse hat mehrere Vorteile und Einschränkungen. 

Im Folgenden findest du ein paar gängige Beispiele:

Pros

• Die Anzahl der Cluster muss nicht angegeben werden: Du kannst nach visueller Prüfung des Dendrogramms wählen.
• Intuitive Visualisierung: Dendrogramme helfen zu verstehen, wie sich Cluster bilden.
• Flexibel: Kann mit verschiedenen Clusterformen umgehen, je nach Verknüpfung und Distanzmetriken.

Nachteile

• Berechnungsintensiv: Nicht ideal für große Datenmengen.
• Empfindlich gegenüber Rauschen und Ausreißern: Ein paar Ausreißer können das Dendrogramm erheblich verzerren.
• Keine Neuzuweisung: Sobald eine Zusammenführung erfolgt ist, kann sie nicht mehr rückgängig gemacht werden, was zu einer suboptimalen Clusterbildung führen kann.

Fazit

Hierarchisches Clustering ist eine vielseitige und interpretierbare Clustering-Technik, die vor allem bei der explorativen Datenanalyse und in Bereichen wie der Genomik und der Kundensegmentierung nützlich ist. Trotz des hohen Rechenaufwands liegt seine Stärke in der Fähigkeit, verschachtelte Gruppierungen aufzudecken, und in der Flexibilität, die Anzahl der Cluster durch die Dendrogramm-Visualisierung post-hoc zu wählen.

Für kleine bis mittelgroße Datensätze, bei denen die Interpretierbarkeit entscheidend ist, ist das hierarchische Clustering nach wie vor eine beliebte Methode für Datenwissenschaftler und Analysten.

Möchtest du mehr über die Details des maschinellen Lernens erfahren? Unser Grundlagen des maschinellen Lernens in Python Lernpfad und Einführung in Hierarchisches Clustering in Python Tutorium sind ein guter Anfang.