Comprendre la distribution de Pareto : Un guide complet

Avez-vous déjà organisé une soirée pizza et remarqué quelque chose d'intéressant ? C'est en tout cas ce que j'ai fait. Lors de ma dernière réunion, j'ai constaté que si la plupart des gens prenaient une ou deux parts, une poignée d'invités dévoraient près de la moitié des pizzas. Alors que je regardais ce qui se passait, j'ai été frappé : J'étais témoin d'un exemple concret de l'un des modèles les plus fascinants de la science des données, la distribution de Pareto.

J'adore cet exemple parce qu'il illustre parfaitement ce qu'est la distribution de Pareto : l'observation que, dans de nombreuses situations, un petit groupe est à l'origine d'une grande partie des résultats.

En tant que scientifique des données, j'ai appris à apprécier la façon dont cette distribution nous aide à comprendre et à modéliser les situations où "les quelques éléments essentiels" dominent "les nombreux éléments insignifiants". Pensez-y : 20 % des clients d'une entreprise génèrent souvent 80 % de son chiffre d'affaires, ou 20 % du contenu d'un site web peut générer 80 % de son trafic. Ce schéma est si courant qu'il est connu sous le nom de principe de Pareto ou de "règle des 80/20", bien que les ratios exacts puissent varier.

Mais ce qui rend la distribution de Pareto vraiment spéciale, c'est qu'il ne s'agit pas d'une simple observation : c'est un outil mathématique puissant qui nous aide à modéliser et à prédire ces schémas déséquilibrés dans les données. Qu'il s'agisse d'analyser les inégalités économiques, d'optimiser les opérations commerciales ou d'étudier les phénomènes naturels, la compréhension de la distribution de Pareto peut fournir des indications précieuses sur les raisons pour lesquelles les choses ne sont pas toujours réparties de manière égale, et sur ce que cela signifie pour notre analyse.

La capacité unique de la distribution de Pareto à mettre en évidence les déséquilibres l'a rendue indispensable dans des domaines allant de l'économie aux sciences naturelles. Si vous êtes impatient d'explorer des modèles statistiques similaires, envisagez de vous plonger dans des ressources telles que Foundations of Probability in Python pour vous familiariser avec les concepts de probabilité, ou Multivariate Probability Distributions in R pour étoffer votre boîte à outils analytique. Pour les apprenants visuels, l'aide-mémoire de l'introduction aux règles de probabilité constitue une excellente référence rapide pour les principes clés.

Qu'est-ce que la distribution de Pareto ?

En 1896, l'économiste italien Vilfredo Pareto a remarqué quelque chose de particulier en regardant son jardin : 20 % de ses cosses de pois contenaient 80 % des pois. Cette observation l'a amené à explorer des modèles similaires de propriété foncière et à découvrir que 80 % des terres italiennes appartenaient à 20 % de la population. Ce qui n'était au départ qu'une simple observation dans un jardin est devenu l'un des outils statistiques les plus polyvalents pour comprendre les distributions inégales.

Historique

À la fin du XIXe siècle, les recherches de Vilfredo Pareto allaient bien au-delà des cosses de pois et de la propriété foncière. Il a analysé les schémas de répartition des richesses dans différents pays et à différentes époques, et a mis en évidence une relation mathématique cohérente. Il a constaté que la minorité riche possédait la majorité des actifs dans toutes les sociétés qu'il a étudiées. Ce modèle est apparu de manière si constante que d'autres chercheurs ont commencé à appliquer ses idées à différents domaines, de l'économie aux sciences naturelles.

La distribution a pris de l'importance lorsque Joseph Juran, consultant en gestion, a pris connaissance des travaux de Pareto en 1937. Juran a appelé ce modèle le "principe de Pareto" et l'a appliqué au contrôle de la qualité, en montrant que la plupart des défauts de fabrication étaient dus à un petit nombre de causes. Cette application a contribué à transformer la gestion de la qualité industrielle et a suscité un intérêt plus large pour les idées de Pareto.

Caractéristiques principales 

La distribution de Pareto se distingue des autres distributions statistiques par plusieurs caractéristiques uniques :

1. Comportement en loi de puissance: Contrairement à la courbe en cloche (distribution normale), où les valeurs extrêmes deviennent exponentiellement rares, la distribution de Pareto suit une loi de puissance. Cela signifie que les valeurs extrêmes sont plus fréquentes que vous ne le pensez.
2. Invariance d'échelle: Si vous zoomez sur une partie d'une distribution de Pareto, le modèle ressemble à l'ensemble. Cette propriété, connue sous le nom d'invariance d'échelle, permet d'expliquer pourquoi la distribution apparaît dans des contextes aussi divers.
3. Le principe 80/20: Si les chiffres exacts peuvent varier (90/10 ou 70/30), l'idée de base demeure : un petit pourcentage de causes crée un grand pourcentage d'effets.
4. Queue lourde: La "queue" de la distribution (la partie représentant les valeurs les plus élevées) diminue plus lentement que les distributions exponentielles. Cette propriété mathématique explique pourquoi les valeurs extrêmes - comme les milliardaires dans la distribution des richesses - se produisent plus souvent qu'une distribution normale ne le prévoirait.

Ces caractéristiques rendent la distribution de Pareto particulièrement adaptée à la modélisation de situations dans lesquelles les ressources, les effets ou les résultats se concentrent dans un petit sous-ensemble de la population.

Formulation mathématique de la distribution de Pareto

Décomposons les mathématiques de la distribution de Pareto en éléments digestes. Les formules peuvent sembler intimidantes au premier abord, mais je vais vous guider pas à pas dans l'étude de chaque élément.

Formule de distribution de Pareto

La fonction de densité de probabilité (PDF) de la distribution de Pareto se présente sous la forme suivante :

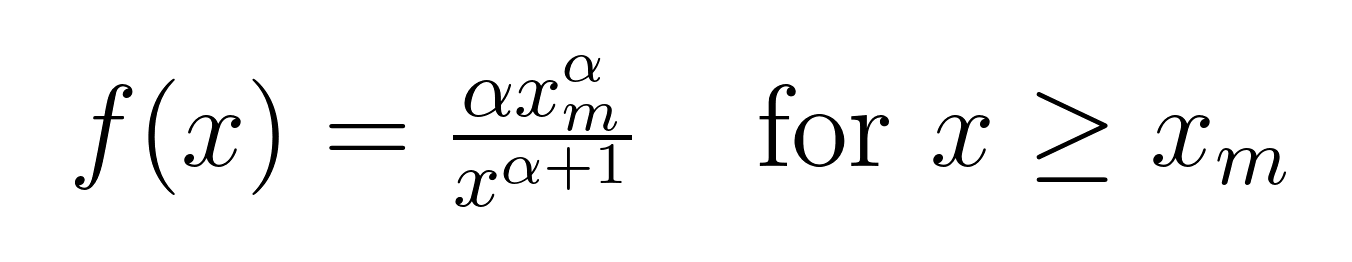
Décodons la signification de chaque symbole :

• x est notre variable aléatoire (comme la richesse, la taille de la ville ou le trafic sur le site web)
• xₘ est la valeur minimale possible de x (également appelée paramètre d'échelle)
• α (alpha) est le paramètre de forme qui détermine la vitesse de chute de la queue

La fonction de distribution cumulative (FDC) nous donne la probabilité qu'une valeur soit inférieure ou égale à x :

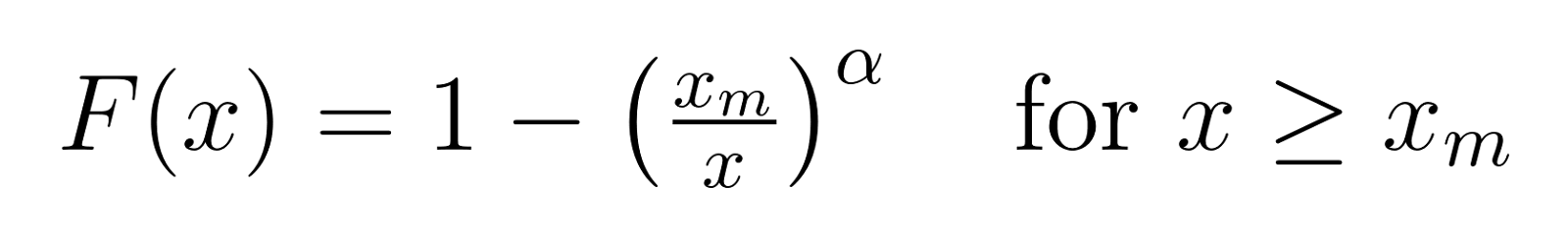
Pour rendre ces formules plus concrètes, examinons ce que signifient différentes valeurs de α :

Comprendre le principe de Pareto

La fameuse règle des 80/20 émerge naturellement de la distribution de Pareto lorsque α ≈ 1,16.

Dans l'analyse des données, ce principe nous aide :

1. Identifier les facteurs à fort impact dans notre ensemble de données
2. Concentrer les ressources sur les variables les plus influentes
3. Prévoir où les valeurs extrêmes peuvent se produire
4. Fixez des attentes réalistes en ce qui concerne la distribution des données

Par exemple, lors de l'analyse des données relatives aux clients, nous pouvons découvrir que :

• 20 % des produits génèrent 80 % des ventes
• 20 % des corrections de bogues résolvent 80 % des plaintes des clients
• 20 % des campagnes de marketing génèrent 80 % des nouvelles inscriptions

Ces informations aident les entreprises à prendre des décisions éclairées sur les domaines dans lesquels elles doivent concentrer leurs efforts pour obtenir un impact maximal.

Applications de la distribution de Pareto

Des politiques économiques aux catastrophes naturelles, la distribution de Pareto apparaît dans des endroits surprenants.

Économie et répartition des richesses

Promenez-vous dans les quartiers financiers de n'importe quel pays et vous verrez la distribution de Pareto à l'œuvre. Les banques et les économistes l'utilisent pour suivre la concentration des richesses, modéliser les disparités de revenus et analyser les politiques fiscales. Par exemple, lorsque des économistes ont étudié la richesse mondiale en 2023, ils ont constaté que les 1 % d'adultes les plus riches possédaient 44 % de la richesse mondiale. Cette répartition aide les décideurs politiques à comprendre les écarts de richesse et à concevoir des interventions économiques. Si vous êtes intéressé par les notions de répartition des richesses, nous avons des tutoriels sur le coefficient de Gini et la courbe de Lorenz.

Entreprises et marketing

Dans le monde des affaires, le principe de Pareto aide les entreprises à travailler plus intelligemment, et non plus durement. Prenons l'exemple d'un site de commerce électronique qui analyse les données de ses clients :

• Segmentation de la clientèle: Identifier et fidéliser les clients VIP qui génèrent le plus de revenus
• Gestion des stocks: Concentrez-vous sur les produits les plus vendus et optimisez le stockage
• Allocation des ressources: Orienter les équipes de vente vers les prospects prometteurs et donner la priorité aux caractéristiques essentielles

Phénomènes naturels et recherche scientifique

La nature suit également les schémas de Pareto. Les scientifiques utilisent cette distribution pour étudier :

• Schémas géographiques: Populations urbaines, réseaux fluviaux, taille des incendies de forêt
• Événements géologiques: Magnitude des tremblements de terre et répliques
• Systèmes biologiques: Abondance des espèces dans les écosystèmes

Prenons l'exemple des tremblements de terre : la distribution de leur magnitude suit un modèle de Pareto, avec de nombreuses petites secousses et de rares tremblements dévastateurs. Cette compréhension aide les sismologues à développer de meilleurs modèles de prévision et d'évaluation des risques.

Visualisation de la distribution de Pareto

La visualisation des données donne vie aux propriétés uniques de la distribution de Pareto. Voyons comment cette distribution se présente graphiquement et ce que ses formes nous apprennent sur les données que nous analysons.

Représentation graphique

La manière la plus courante de visualiser la distribution de Pareto est sa fonction de densité de probabilité (PDF). Cela nous montre comment les valeurs sont réparties dans notre ensemble de données.

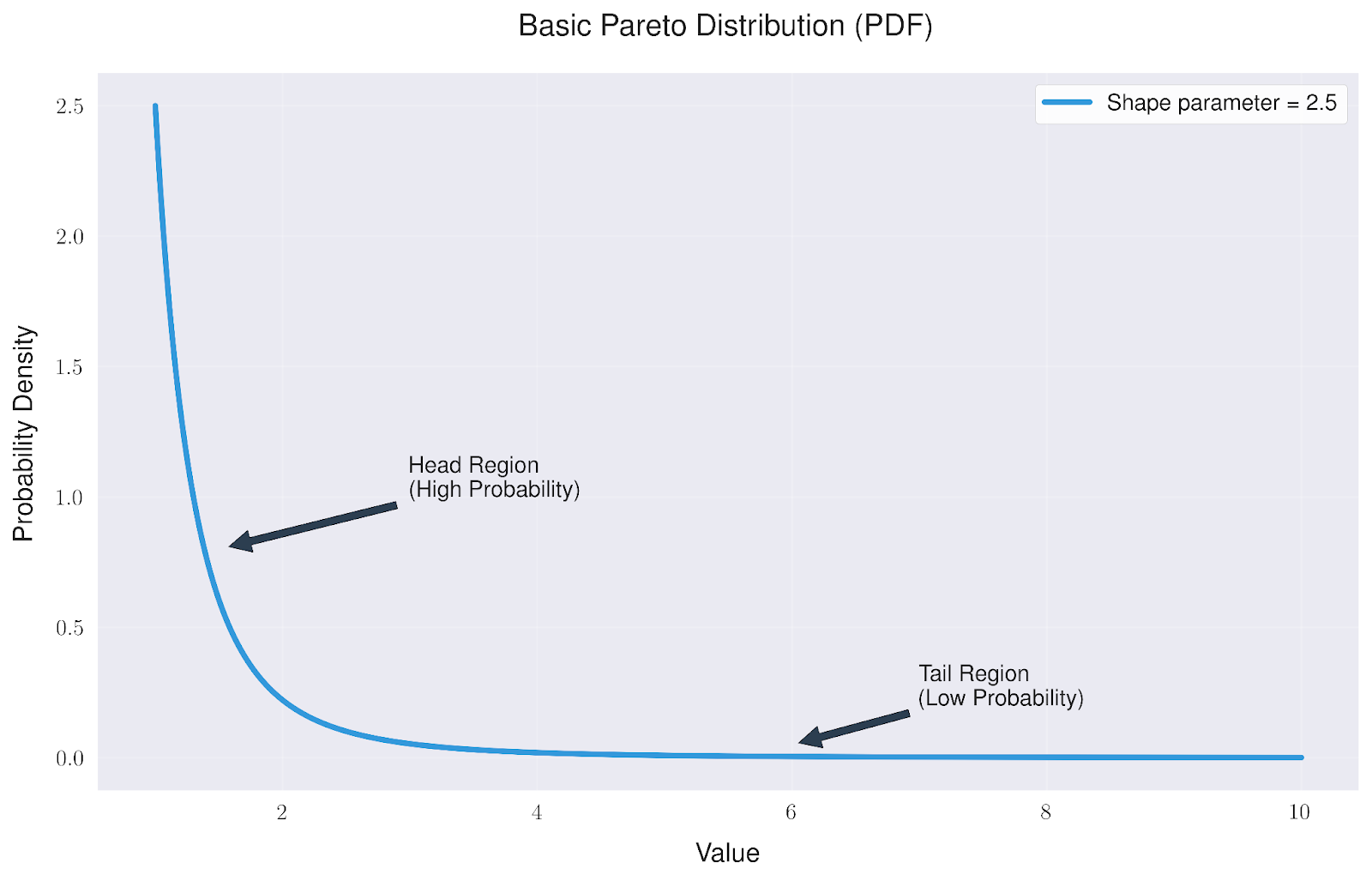
La distribution de base de Pareto a une forme particulière qui nous indique deux choses importantes :

1. La région de la "tête" présente une forte concentration de probabilité près de la valeur minimale
2. La région de la "queue" s'étend loin vers la droite, ce qui montre que si les valeurs extrêmes sont rares, elles sont plus fréquentes que dans beaucoup d'autres distributions

Ce qui rend la distribution de Pareto particulièrement intéressante, c'est la façon dont elle évolue en fonction de différents paramètres de forme. Ces paramètres influencent directement le degré d'extrémisme de nos valeurs.

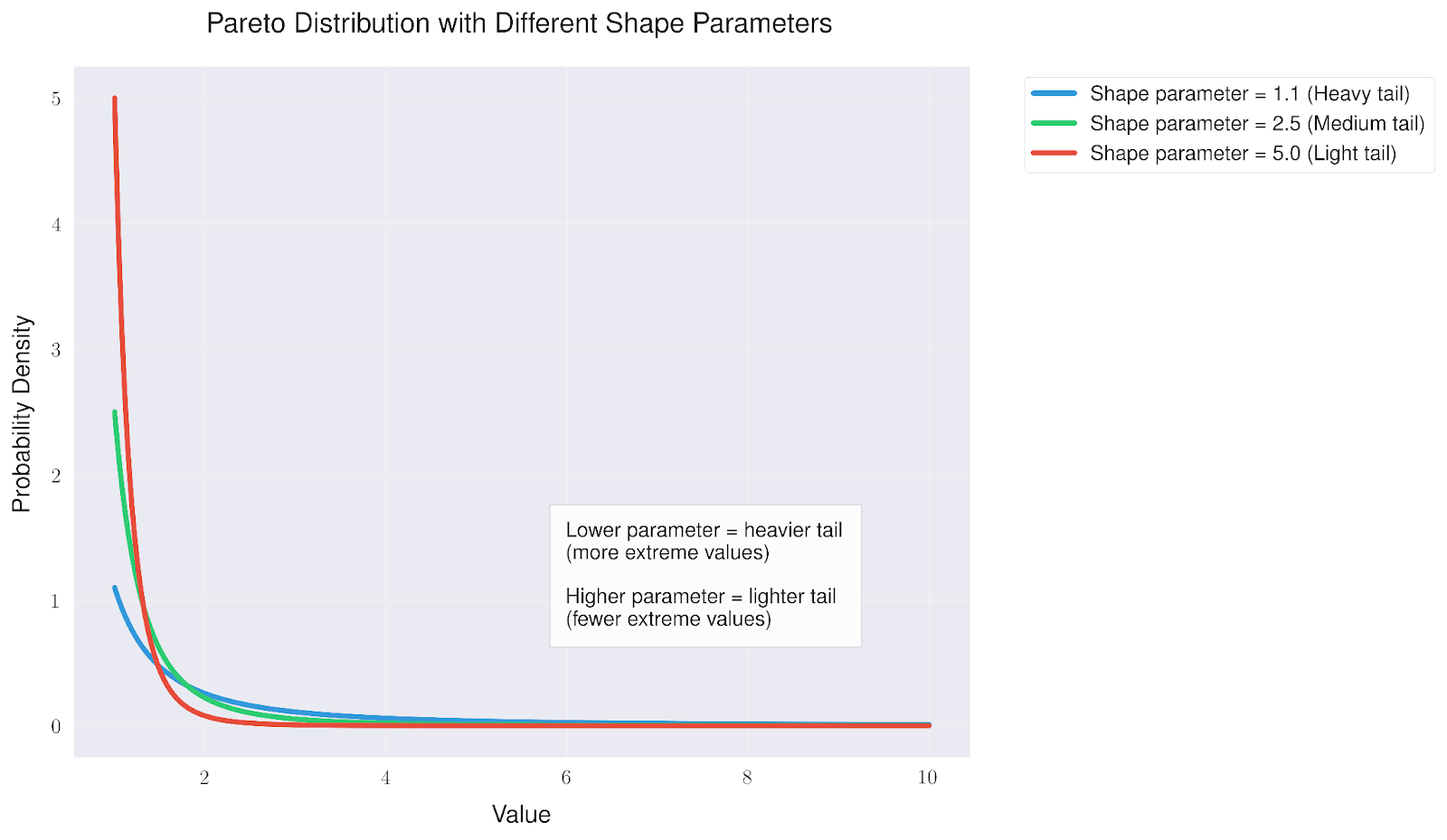
L'examen des différents paramètres de forme révèle que

• Des valeurs plus faibles (comme 1,1) créent une "queue lourde" où les valeurs extrêmes sont plus susceptibles de se produire.
• Les valeurs moyennes (environ 2,5) offrent un équilibre entre les événements courants et les événements extrêmes.
• Des valeurs plus élevées (comme 5,0) créent une "queue légère" où les valeurs extrêmes deviennent de plus en plus rares.

Cette flexibilité rend la distribution de Pareto utile pour modéliser divers phénomènes du monde réel, de la distribution des richesses (souvent à queue lourde) aux défauts de fabrication (généralement à queue plus légère).

La distribution de la richesse est souvent à queue lourde, ce qui implique une probabilité non négligeable de valeurs extrêmement élevées, de sorte que les événements rares mais massifs (comme les milliardaires) ont un impact important. C'est logique, car il y a un effet de composition, puisque les personnes qui ont de l'argent peuvent investir. Les distributions à queue légère (comme certains types de défauts de fabrication) se décomposent plus rapidement en raison de processus limités et stables, ce qui signifie que les valeurs extrêmes sont beaucoup moins probables puisque les grands écarts sont rares.

Outils de visualisation

Pour visualiser la distribution de Pareto, nous nous appuyons principalement sur des langages de programmation statistique et des logiciels spécialisés. Python s'impose comme un choix populaire, offrant des bibliothèques puissantes comme scipy.stats pour les calculs, ainsi que matplotlib et seaborn pour la création de visualisations claires et de qualité. R excelle également dans ce domaine, avec ses fonctions statistiques intégrées robustes et le paquetage polyvalent ggplot2 pour le traçage. 

Si Excel est excellent pour créer des diagrammes de Pareto (diagrammes à barres illustrant le principe 80/20), ce n'est pas le meilleur outil pour visualiser et travailler avec la distribution de probabilité de Pareto elle-même. Pour une analyse statistique et une visualisation correctes de la distribution de Pareto, nous vous recommandons d'utiliser les outils de programmation mentionnés ci-dessus.

Pour vous aider à mieux comprendre la visualisation des distributions de probabilités, plusieurs ressources peuvent vous servir de point de départ. Le didacticiel Distributions de probabilités en Python propose une expérience pratique de la mise en œuvre de diverses distributions, y compris des exemples détaillés utilisant les bibliothèques statistiques de Python. Pour ceux qui s'intéressent aux aspects visuels, l'article Visualisations de données qui capturent les distributions couvre des techniques spécifiquement conçues pour représenter efficacement les distributions statistiques. Enfin, l'aide-mémoire sur la visualisation des données sert de référence rapide pour choisir et créer des visualisations appropriées pour différents types de données distribuées. L'ensemble de ces ressources constitue une bonne base pour comprendre et visualiser la distribution de Pareto.

Limites et défis de la distribution de Pareto

Chaque outil statistique a ses limites, et la distribution de Pareto ne fait pas exception. Bien qu'il s'agisse d'une lentille puissante pour visualiser certains types de données, il est tout aussi important de savoir quand ne pas l'utiliser que de savoir quand elle est parfaitement adaptée. Permettez-moi de vous faire part de quelques considérations essentielles auxquelles j'ai appris à prêter attention lorsque je travaille avec cette distribution.

Hypothèses et contraintes

Considérez la distribution de Pareto comme un objectif d'appareil photo spécialisé : il fonctionne parfaitement pour certaines prises de vue, mais peut en déformer d'autres. Ses hypothèses de base constituent les spécifications techniques que nous devons respecter :

Tout d'abord, il y a l' exigence de valeur minimale. Contrairement à d'autres distributions qui peuvent traiter n'importe quel nombre, la distribution de Pareto a besoin d'un point de départ clair au-dessus de zéro. C'est comme une mise minimale au casino : vous ne pouvez pas jouer avec moins que ce montant. Cela devient particulièrement délicat lorsque vos données comprennent des zéros ou des valeurs négatives, par exemple lors du cursus des scénarios de pertes et profits.

La distribution suppose également que chaque événement est isolé, indépendant des autres. Mais la vie réelle fonctionne rarement de cette manière. Prenons l'exemple de l'accumulation de richesses : le fait d'avoir de l'argent permet souvent de gagner plus facilement de l'argent. Ces interconnexions peuvent rendre la distribution de Pareto moins précise que ce que l'on pourrait espérer.

Ce qui est peut-être le plus intrigant, c'est que la distribution suppose l'invariance d'échelle, c'est-à-dire l'idée que les différences relatives ont plus d'importance que les différences absolues. Bien que cela soit souvent vrai, les scénarios du monde réel dérogent parfois à cette règle. L'impact d'un doublement de la richesse d'une personne, par exemple, est très différent selon le niveau de richesse.

Interprétations erronées et pièges courants

D'après mon expérience, même les analystes expérimentés peuvent tomber dans plusieurs pièges lorsqu'ils travaillent avec la distribution de Pareto. 

La plus courante est la généralisation abusive. Ce n'est pas parce que vous observez un schéma de type 80/20 qu'il s'agit automatiquement d'une distribution de Pareto. C'est comme si vous supposiez que tous les oiseaux que vous voyez sont des aigles - la forme peut être similaire, mais les détails comptent. Testez toujours l'adéquation de votre distribution avant de tirer des conclusions.

L'estimation des paramètres représente un autre défi. Le paramètre de forme (α) peut être particulièrement sensible aux valeurs aberrantes, surtout pour les petits ensembles de données. C'est comme essayer de mesurer la taille moyenne d'une population - quelques individus très grands ou très petits peuvent fausser considérablement vos résultats si la taille de votre échantillon est trop petite.

Lorsqu'il s'agit de prévoir des événements extrêmes, la queue épaisse de la distribution de Pareto peut être à la fois une bénédiction et une malédiction. Bien qu'il soit excellent pour modéliser la possibilité de résultats extrêmes, il peut parfois suggérer qu'ils sont plus probables qu'ils ne le sont en réalité. Ceci est particulièrement important dans les scénarios d'évaluation des risques - vous ne voulez pas surestimer ou sous-estimer les événements rares.

Enfin, il y a ce que j'appelle la "cécité contextuelle", c'est-à-dire le fait d'être tellement pris par l'élégance mathématique de la distribution que l'on oublie de se demander si elle a un sens dans notre situation spécifique. N'oubliez pas que la carte n'est pas le territoire et que la distribution de Pareto n'est qu'une carte parmi d'autres.

En cas de doute, envisagez des distributions alternatives et validez toujours vos hypothèses par rapport à la connaissance réelle de votre domaine. Après tout, les statistiques doivent servir notre compréhension de la réalité, et non l'inverse.

Le principe de Pareto dans la vie réelle

Le schéma directeur de la nature dans la dynamique des écosystèmes

Dans les écosystèmes naturels, le principe de Pareto se manifeste à travers le concept fascinant des espèces clés de voûte, ces quelques organismes qui exercent une influence considérable sur leur environnement. Voyez comment les loups de Yellowstone influencent tout, des populations d'élans au tracé des rivières, ou comment les récifs coralliens, qui ne représentent qu'une infime partie de l'espace océanique, abritent près d'un quart de toutes les espèces marines. Cette répartition naturelle de 80/20 se retrouve dans tous les domaines, de la taille de la canopée des arbres à la répartition des précipitations entre les saisons.

La symphonie de la répartition des richesses

Pensez à la répartition des richesses comme à un concert d'orchestre, où quelques instruments clés portent la mélodie principale tandis que d'autres fournissent un soutien essentiel en arrière-plan. Tout comme le premier violon dirige souvent l'orchestre, un petit pourcentage d'individus détient la majorité de la richesse mondiale, ce qui crée une composition économique complexe. Ce schéma a de profondes implications pour la politique économique, car il soulève des questions sur la manière de maintenir à la fois le dynamisme que la concentration des richesses peut engendrer et l'harmonie sociale qui exige une participation plus large. La compréhension de ce parallèle musical nous permet d'apprécier à la fois l'efficacité et les défis de la concentration des richesses.

La règle de l'innovation : quand le moins crée le plus

Dans le domaine de l'innovation, le principe de Pareto se manifeste dans la façon dont les idées révolutionnaires émergent d'un sous-ensemble étonnamment petit de tentatives. Des entreprises comme Apple et Google ont constaté qu'environ 20 % de leurs produits généraient 80 % de leurs revenus, tandis que dans la recherche scientifique, une petite fraction d'articles recueille la majorité des citations. Cette tendance se retrouve dans toutes les industries créatives, qu'il s'agisse de chansons à succès dans les catalogues musicaux ou de films à succès dans les portefeuilles des studios.

Ondes sociales : l'effet de réseau

Le principe de Pareto s'applique à la manière dont l'information se propage dans les réseaux sociaux. Quelques influenceurs triés sur le volet, représentant peut-être 20 % des utilisateurs, sont souvent à l'origine de 80 % de l'engagement sur les plateformes sociales. Ce même schéma se retrouve dans la viralité du contenu, où un petit pourcentage de posts capte la majorité des partages et des interactions.

Conclusion

La distribution de Pareto montre comment les outils statistiques peuvent révéler des schémas de concentration significatifs dans les données. Pour vous permettre de mieux comprendre ces concepts, nous vous offrons de précieuses possibilités d'apprentissage. Notre cours Fondations des probabilités en R présente les principes de base, tandis que le cours Introduction à l'analyse de portefeuille en R montre comment ces idées s'appliquent aux contextes financiers. En outre, notre tutoriel Probabilités et statistiques du poker avec Python offre une façon unique d'explorer les concepts de probabilité en action, rendant l'apprentissage à la fois engageant et pratique. Ces ressources fournissent une base solide pour appliquer les connaissances statistiques à toute une série de scénarios pratiques.