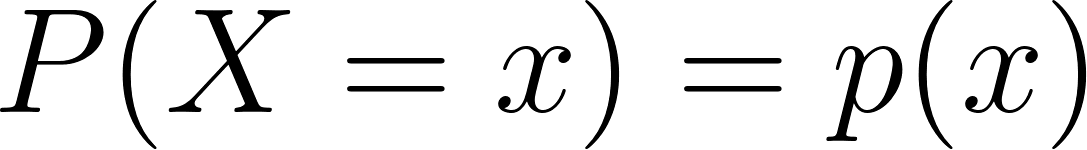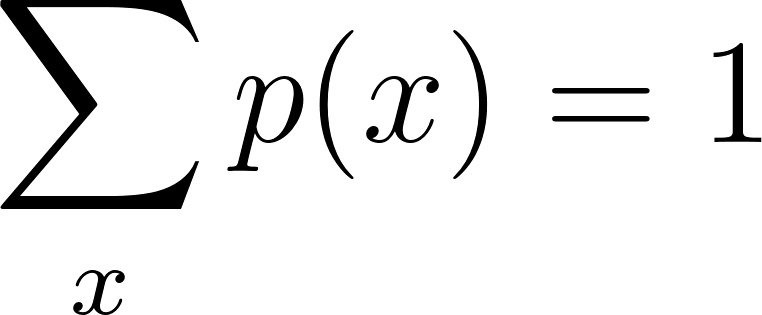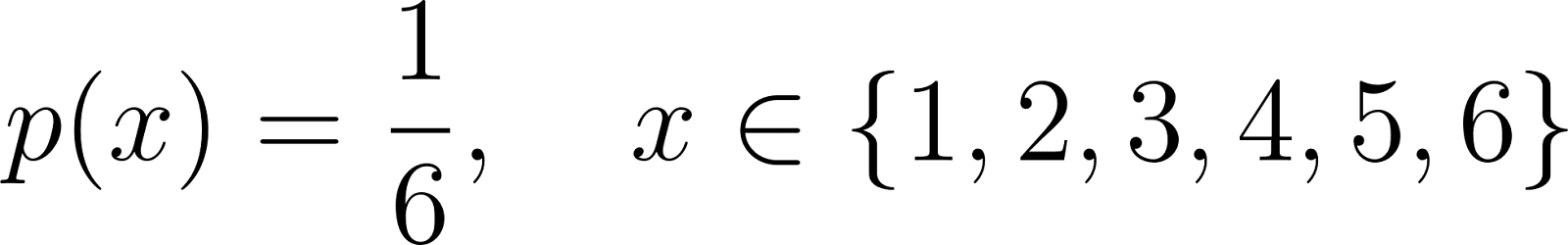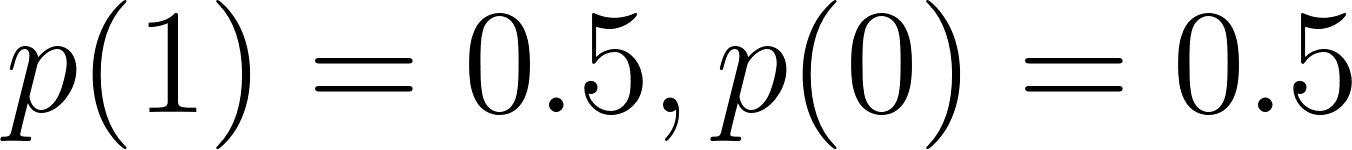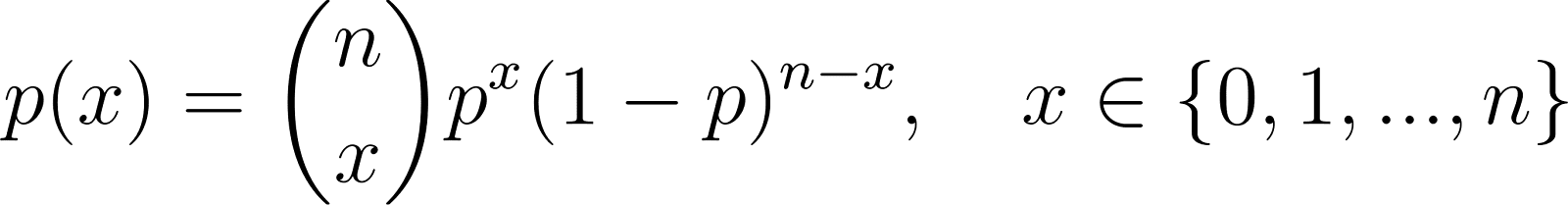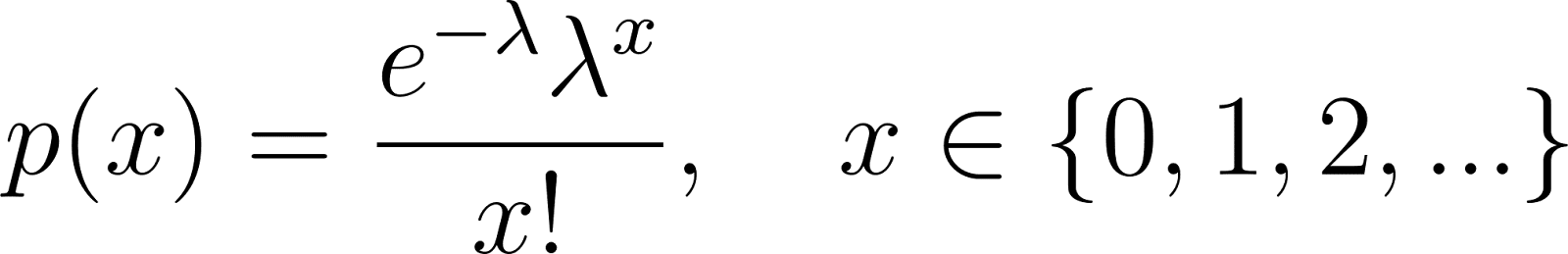Cours
En probabilité et en statistique, la probabilité d'un résultat pour les variables aléatoires discrètes est quantifiée par la fonction de masse de probabilité (PMF), tandis que pour les variables continues, nous utilisons la fonction de densité de probabilité (PDF).
Qu'il s'agisse de modéliser des tirages à pile ou face, des pannes d'équipement ou des clics d'utilisateurs sur une page web, le CMR nous aide à quantifier la probabilité de différents résultats.
Comprendre la fonction de masse de probabilité
La formule de la fonction de masse de probabilité
Mathématiquement, la fonction de masse de probabilité d'une variable aléatoire discrète est la suivante X est définie comme suit :
Où ?
- X est une variable aléatoire discrète,
- x est une valeur que X peut prendre,
- p(x) est la probabilité que X soit égal à x.
Deux conditions essentielles doivent être remplies pour que le CMR soit valable :
1. Non-négativité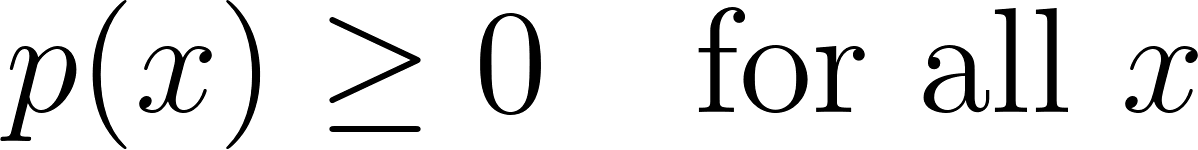
2. La probabilité totale doit être égale à un
Ces conditions garantissent que toutes les probabilités attribuées ont un sens logique et mathématique. Le CMR fournit une description complète de la distribution de X, ce qui permet de calculer les valeurs attendues, les variances et d'autres mesures statistiques.
Définition et propriétés principales
Le CMR présente plusieurs caractéristiques qui le distinguent :
- Discrétion: Le CMR ne s'applique qu'aux variables aléatoires discrètes, celles qui peuvent prendre des valeurs dénombrables (comme 0, 1, 2, ...).
- Normalisation: La somme du CMR sur toutes les valeurs possibles de X doit être exactement égale à 1.
- Attribution de probabilités individuelles: Chaque valeur possible x se voit attribuer une probabilité spécifique p(x), qui reflète la probabilité de ce résultat particulier.
Par exemple, le CMR d'un dé à six faces équitable est le suivant :
Ici, chaque valeur de 1 à 6 a une chance égale d'apparaître, et la somme de toutes les probabilités est de 1.
Fonction de masse de probabilité vs. Fonction de densité de probabilité
Comprenons en détail les différences entre les CMR et les PDF et la manière dont ils modélisent lesdistributions discrètes etcontinues, respectivement :
|
Caractéristique |
PMF |
|
|
Type de variable |
Discret |
En continu |
|
Valeur de sortie |
||
|
Règle de totalisation |
Exemple de CMR
Prenons un exemple classique de PMF : tirer à pile ou face une pièce de monnaie (essai de Bernoulli) :
Effectuons un essai de Bernoulli en Python pour mieux comprendre.
import matplotlib.pyplot as plt
from scipy.stats import bernoulli
# Parameters
p = 0.5 # Probability of Heads
# PMF for a fair coin
x = [0, 1] # 0 = Tails, 1 = Heads
pmf_values = bernoulli.pmf(x, p)
# Plotting
plt.bar(x, pmf_values, tick_label=['Tails (0)', 'Heads (1)'])
plt.title('PMF of a Fair Coin Toss (Bernoulli Trial)')
plt.ylabel('Probability')
plt.xlabel('Outcome')
plt.grid(axis='y', linestyle='--')
plt.show()
Exemple de PDF
Voici un exemple de PDF : mesure de la taille d'une personne (variable continue).
Le PDF pourrait montrer que la densité de probabilité est la plus élevée autour de 170 cm, mais la probabilité d'une taille exacte est techniquement égale à 0.
Une fois encore, nous allons comprendre cela à l'aide d'un exemple de code.
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
# Parameters
mu = 170 # mean height
sigma = 10 # standard deviation
# Continuous range of heights
x = np.linspace(130, 210, 500)
pdf_values = norm.pdf(x, mu, sigma)
# Plotting
plt.plot(x, pdf_values, label='PDF')
plt.title('PDF of Human Height (Normal Distribution)')
plt.xlabel('Height (cm)')
plt.ylabel('Probability Density')
plt.grid(True)
plt.axvline(mu, color='red', linestyle='--', label='Mean (170 cm)')
plt.legend()
plt.show()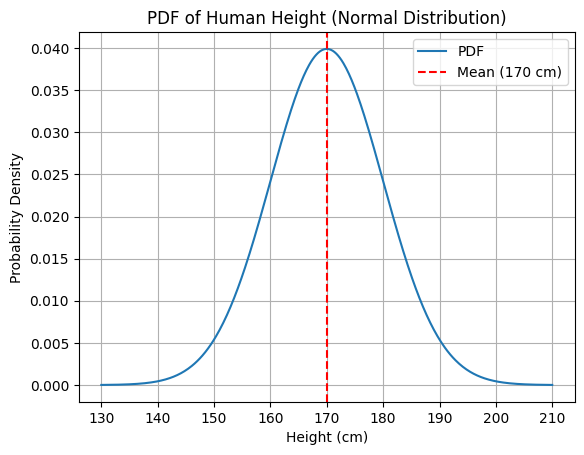
Alors que les CMR attribuent des probabilités réelles à des résultats spécifiques, les PDF décrivent la probabilité relative des résultats à l'intérieur d'un intervalle.
Distributions discrètes courantes à l'aide de PMF
Les distributions de Bernoulli, binomiale, géométrique et de Poisson sont des exemples courants de distributions de probabilités discrètes. Jetons un coup d'œil à chacun d'entre eux.
PMF de la distribution de Bernoulli
La distribution de Bernoulli modélise une expérience unique avec seulement deux résultats possibles : la réussite (1) et l'échec (0).
Où p est la probabilité de réussite.
En voici un exemple : Lancer une pièce de monnaie équitable où le succès est égal à la tête :
PMF de la distribution binomiale
La distribution binomiale généralise la distribution de Bernoulli aux essais multiples :
Où ?
- n est le nombre d'essais indépendants,
- p est la probabilité de réussite de chaque essai,
- x est le nombre de succès.
Un exemple serait de compter les articles défectueux dans un lot de produits.
PMF de la distribution géométrique
La distribution géométrique est utilisée pour modéliser le nombre d'échecs avant le premier succès dans des essais de Bernoulli répétés et indépendants :
Un exemple courant serait le nombre de lancers de pièces jusqu'à ce que la première tête apparaisse.
PMF de la distribution de Poisson
La distribution de Poisson modélise le nombre d'événements dans un intervalle de temps ou d'espace fixe :
Où λ est le nombre attendu d'événements par intervalle.
Le nombre d'arrivées de clients par heure dans un centre de services en est un exemple.
Visualisation des fonctions de masse de probabilité
Les CMR sont visualisés à l'aide de diagrammes à barres, où :
- L'axe des x représente les valeurs possibles de la variable aléatoire.
- L'axe des ordonnées représente la probabilité attribuée par le CMR.
Voici un tableau illustrant un exemple : lancer un dé juste
|
X |
1 |
2 |
3 |
4 |
5 |
6 |
|
P(X) |
1/6 |
1/6 |
1/6 |
1/6 |
1/6 |
1/6 |
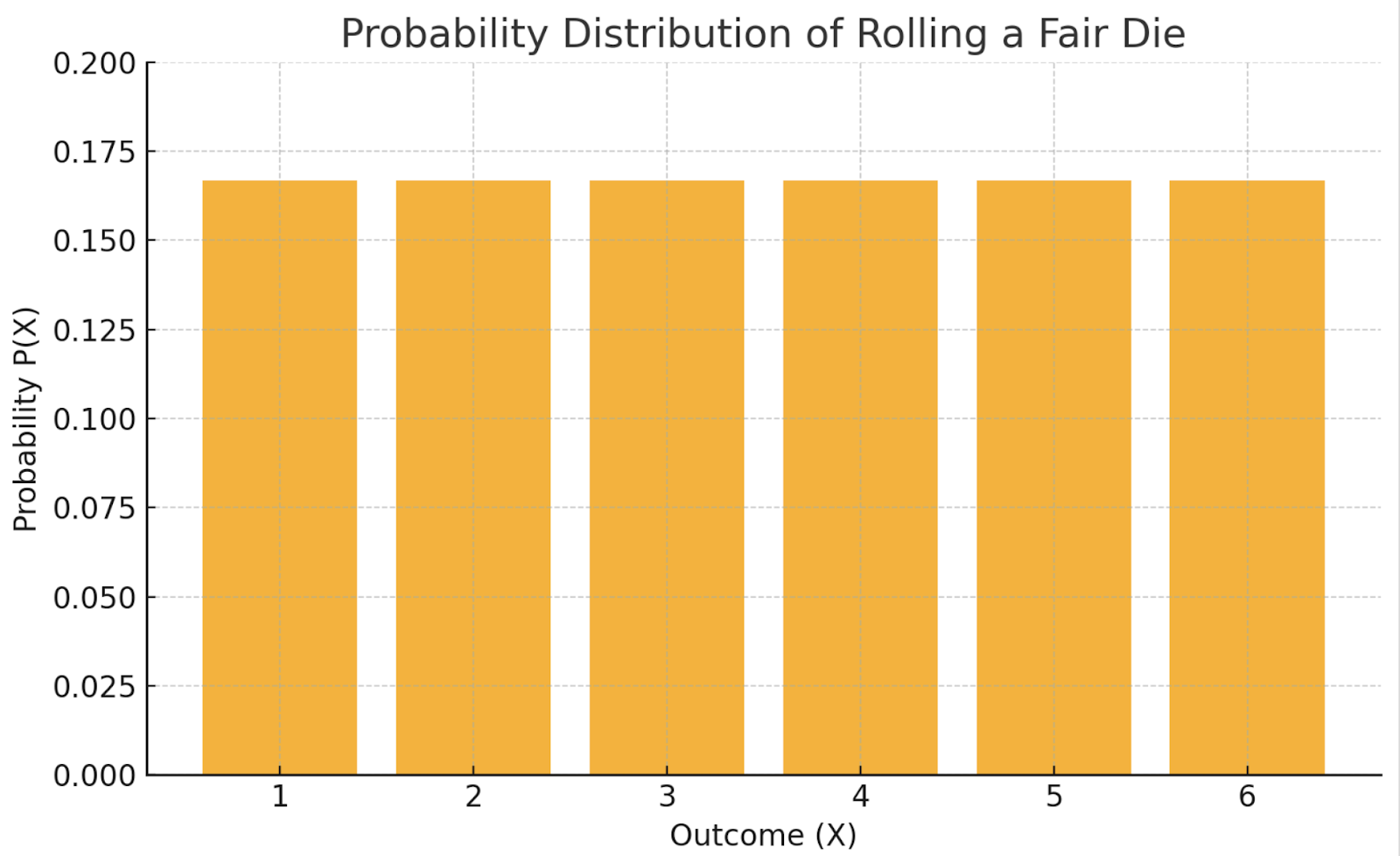
Ce CMR uniforme apparaîtrait sous la forme d'un diagramme à barres plat, où toutes les issues sont également probables.
De telles visualisations facilitent l'analyse :
- Interpréter les distributions de manière intuitive,
- Comparez les probabilités relatives,
- Repérer les distributions asymétriques ou symétriques.
Applications des fonctions de masse de probabilité
Les CMR sont utilisés dans différents domaines :
Statistiques
Pour le calcul des valeurs attendues :
et les écarts :
Apprentissage automatique
Dans les algorithmes de classification (par exemple, Naive Bayes), les CMR décrivent les vraisemblances des caractéristiques catégorielles. Les modèles probabilistes tels que les modèles de Markov cachés dépendent également des FMP pour les transitions d'état et les émissions.
Ingénierie de la fiabilité
Les CMR permettent de déterminer la probabilité de défaillance d'un système ou d'un composant à un moment donné.
Économie et finance
Modélisation de scénarios de marché ou de résultats d'investissement lorsque le nombre de résultats est fini et distinct.
Inférence bayésienne
Les CMR servent de distributions préalables dans les modèles bayésiens discrets. Lorsque de nouvelles données sont observées, le CMR antérieur est mis à jour en un CMR postérieur, ce qui rend la mise à jour bayésienne traçable pour les problèmes discrets.
Si vous souhaitez en savoir plus sur le fonctionnement des probabilités conditionnelles, consulteznotre site Probabilité conditionnelle : Un examen approfondi tutoriel.
Simulations de Monte Carlo
Les CMR sont également essentiels dans les simulations de Monte Carlo, en particulier pour les systèmes dont les résultats sont discrets et probabilistes. Ces simulations utilisent un échantillonnage aléatoire à partir d'un CMR pour estimer le comportement ou la performance d'un modèle sur de nombreuses itérations.
Conclusion
La fonction de masse de probabilité fournit la structure mathématique permettant de modéliser des variables aléatoires discrètes, contrairement aux PDF, qui traitent de variables continues. Ils permettent une modélisation puissante dans tous les domaines, des simples tirages à pile ou face aux systèmes complexes d'apprentissage automatique.
Principaux enseignements :
- Les CMR sont non négatifs et leur somme est égale à 1 pour toutes les valeurs possibles.
- Ils définissent la forme et les caractéristiques des distributions de probabilités discrètes.
- Les PMF sont essentiels dans de nombreuses applications, des statistiques classiques à l'IA moderne et à la finance.
- Dans l'inférence bayésienne et les méthodes de Monte Carlo, les CMR sont essentiels pour mettre à jour les croyances et simuler des systèmes incertains.
Pour ceux qui approfondissent la théorie des probabilités, l'exploration des fonctions de distribution cumulative (FDC) et le calcul de la valeur attendue enrichiront votre compréhension de la manière dont l'incertitude peut être quantifiée et exploitée dans la prise de décision. Découvrez nos cours :

Je suis un stratège de l'IA et un éthicien qui travaille à l'intersection de la science des données, du produit et de l'ingénierie pour construire des systèmes d'apprentissage automatique évolutifs. Considéré comme l'un des 200 plus grands innovateurs commerciaux et technologiques au monde, je me suis donné pour mission de démocratiser l'apprentissage automatique et de briser le jargon pour que tout le monde puisse participer à cette transformation.
FAQ sur le CMR
Qu'est-ce qu'une fonction de masse de probabilité ?
A Le CMR attribue des probabilités aux résultats discrets d'une variable aléatoire, en veillant à ce que la somme de toutes les valeurs soit égale à 1.
Quelle est la différence entre un CMR et un PDF ?
Un CMR s'applique à des variables discrètes, tandis qu'un PDF s'applique à des variables continues.
Un CMR peut-il être négatif ?
Non, un CMR doit toujours être non négatif.
Quelles sont les distributions courantes qui utilisent les CMR ?
Les distributions de Bernoulli, Binomiale, Géométrique et de Poisson en sont des exemples.
Comment le CMR est-il utilisé dans des applications réelles ?
Les CMR sont largement utilisés dans les domaines de l'apprentissage automatique, de la finance, de l'ingénierie de la fiabilité et de la modélisation statistique.