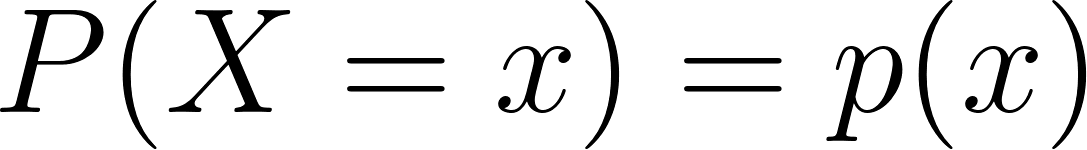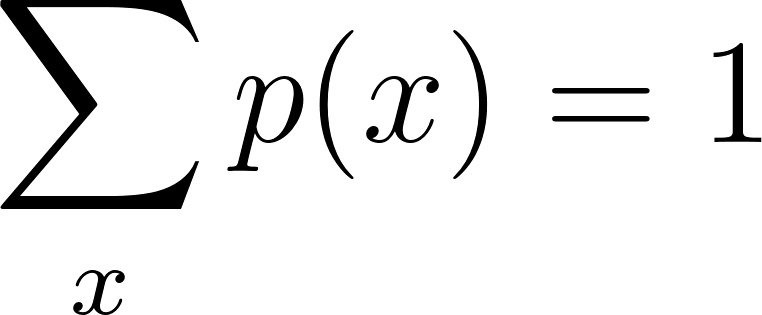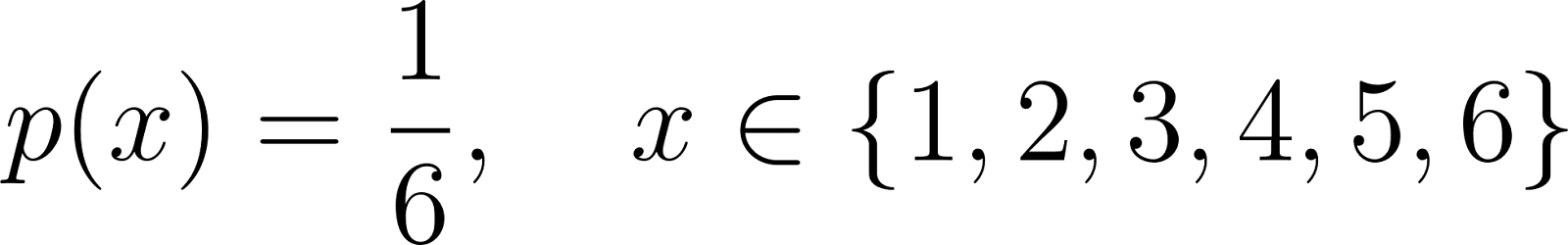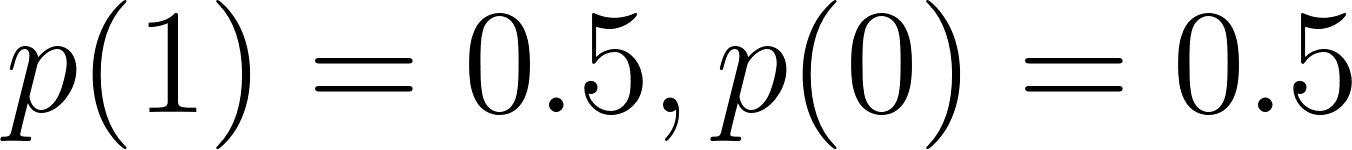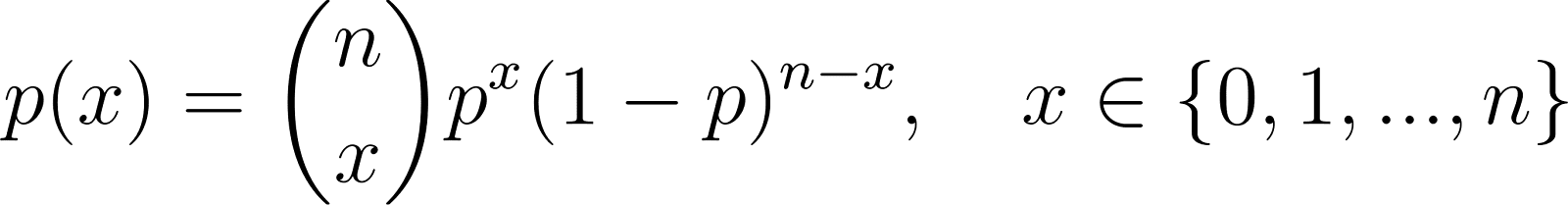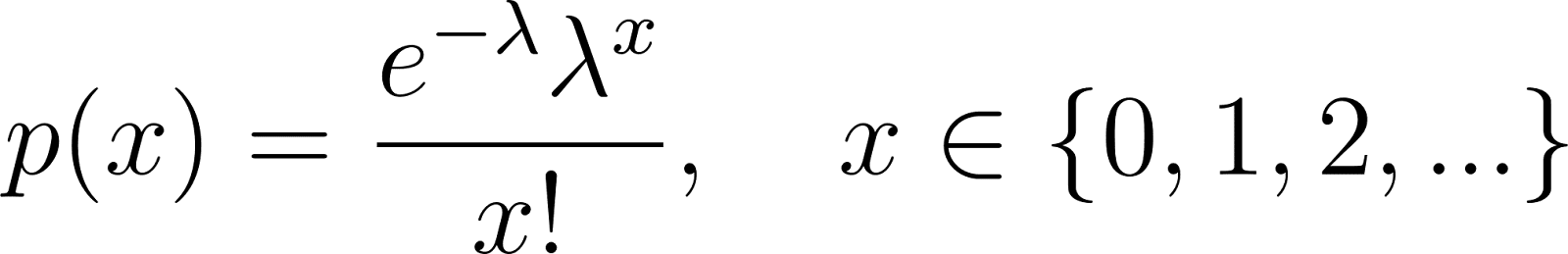Curso
En probabilidad y estadística, la probabilidad de un resultado para variables aleatorias discretas se cuantifica mediante la función de masa de probabilidad (FMP), mientras que para variables continuas, utilizamos la función de densidad de probabilidad (FDP).
Ya sea modelando lanzamientos de monedas, fallos de equipos o clics de los usuarios en una página web, el PMF nos ayuda a cuantificar la probabilidad de diferentes resultados.
Comprender la función de masa de probabilidad
La fórmula de la función de masa de probabilidad
Matemáticamente, la función de masa de probabilidad de una variable aleatoria discreta X se define como
Dónde:
- X es una variable aleatoria discreta,
- x es un valor que puede tomar X,
- p(x) es la probabilidad de que X sea igual a x.
Para que un PMF sea válido deben cumplirse dos condiciones críticas:
1. No negatividad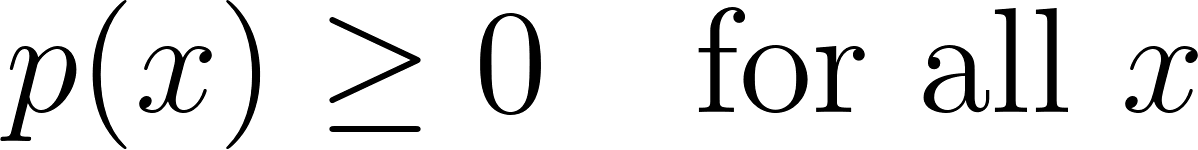
2. La probabilidad total debe ser igual a uno
Estas condiciones garantizan que todas las probabilidades asignadas tengan sentido lógico y matemático. El PMF proporciona una descripción completa de la distribución de X, lo que permite calcular valores esperados, varianzas y otras medidas estadísticas.
Definición y propiedades clave
La PMF tiene varias propiedades definitorias que la distinguen:
- Discreción: El PMF sólo se aplica a las variables aleatorias discretas, las que pueden tomar valores contables (como 0, 1, 2, ...).
- Normalización: La suma de la PMF sobre todos los valores posibles de X debe ser exactamente 1.
- Asignación de probabilidad individual: A cada posible valor x se le asigna una probabilidad específica p(x), que capta la probabilidad de ese resultado concreto.
Por ejemplo, el PMF para lanzar un dado justo de seis caras es:
Aquí, cada valor de 1 a 6 tiene la misma probabilidad de aparecer, y la suma de todas las probabilidades es 1.
Función de masa de probabilidad vs. Función de densidad de probabilidad
Comprendamos en detalle las diferencias entre las PMF y las PDF y cómo modelan lasdistribuciones discreta ycontinua, respectivamente:
|
Característica |
PMF |
|
|
Tipo de variable |
Discreto |
Continuo |
|
Valor de salida |
||
|
Regla de suma |
Ejemplo de PMF
Tomemos un ejemplo clásico de PMF: lanzar una moneda justa (ensayo de Bernoulli):
Vamos a realizar un ensayo de Bernoulli en Python para entenderlo mejor.
import matplotlib.pyplot as plt
from scipy.stats import bernoulli
# Parameters
p = 0.5 # Probability of Heads
# PMF for a fair coin
x = [0, 1] # 0 = Tails, 1 = Heads
pmf_values = bernoulli.pmf(x, p)
# Plotting
plt.bar(x, pmf_values, tick_label=['Tails (0)', 'Heads (1)'])
plt.title('PMF of a Fair Coin Toss (Bernoulli Trial)')
plt.ylabel('Probability')
plt.xlabel('Outcome')
plt.grid(axis='y', linestyle='--')
plt.show()
Ejemplo PDF
He aquí un ejemplo en PDF: medir la altura de una persona (variable continua).
La PDF puede mostrar que la densidad de probabilidad es mayor alrededor de 170 cm, pero la probabilidad de cualquier altura exacta es técnicamente 0.
De nuevo, vamos a entenderlo con un ejemplo de código.
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
# Parameters
mu = 170 # mean height
sigma = 10 # standard deviation
# Continuous range of heights
x = np.linspace(130, 210, 500)
pdf_values = norm.pdf(x, mu, sigma)
# Plotting
plt.plot(x, pdf_values, label='PDF')
plt.title('PDF of Human Height (Normal Distribution)')
plt.xlabel('Height (cm)')
plt.ylabel('Probability Density')
plt.grid(True)
plt.axvline(mu, color='red', linestyle='--', label='Mean (170 cm)')
plt.legend()
plt.show()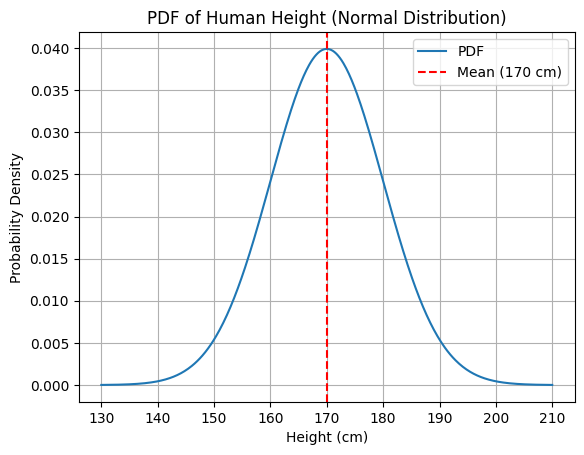
Mientras que las PMF asignan probabilidades reales a resultados concretos, las PDF describen la probabilidad relativa de los resultados dentro de un intervalo.
Distribuciones discretas comunes mediante PMF
Ejemplos comunes de distribuciones discretas de probabilidad son las distribuciones Bernoulli, binomial, geométrica y de Poisson. Echemos un vistazo a cada uno de ellos.
PMF de la distribución Bernoulli
La distribución Bernoulli modela un único experimento con sólo dos resultados posibles: éxito (1) y fracaso (0).
Donde p es la probabilidad de éxito.
He aquí un ejemplo: Lanzar una moneda justa en la que el éxito = cara:
PMF de la distribución binomial
La distribución Binomial generaliza la Bernoulli a múltiples ensayos:
Dónde:
- n es el número de ensayos independientes,
- p es la probabilidad de éxito en cada ensayo,
- x es el número de aciertos.
Un ejemplo sería contar los artículos defectuosos de un lote de productos.
PMF de la distribución Geométrica
La distribución Geométrica se utiliza para modelar el número de fallos antes del primer éxito en ensayos Bernoulli independientes repetidos:
Un ejemplo habitual sería el número de lanzamientos de una moneda hasta que aparezca la primera cara.
PMF de la distribución de Poisson
La distribución de Poisson modela el número de sucesos en un intervalo fijo de tiempo o espacio:
Donde λ es el número esperado de sucesos por intervalo.
Un ejemplo de ello es el número de llegadas de clientes a un centro de servicio por hora.
Visualización de las funciones de masa de probabilidad
Los PMF se visualizan mediante gráficos de barras, donde:
- El eje x representa los posibles valores de la variable aleatoria.
- El eje y representa la probabilidad asignada por el PMF.
He aquí una tabla que muestra un ejemplo: lanzar un dado justo
|
X |
1 |
2 |
3 |
4 |
5 |
6 |
|
P(X) |
1/6 |
1/6 |
1/6 |
1/6 |
1/6 |
1/6 |
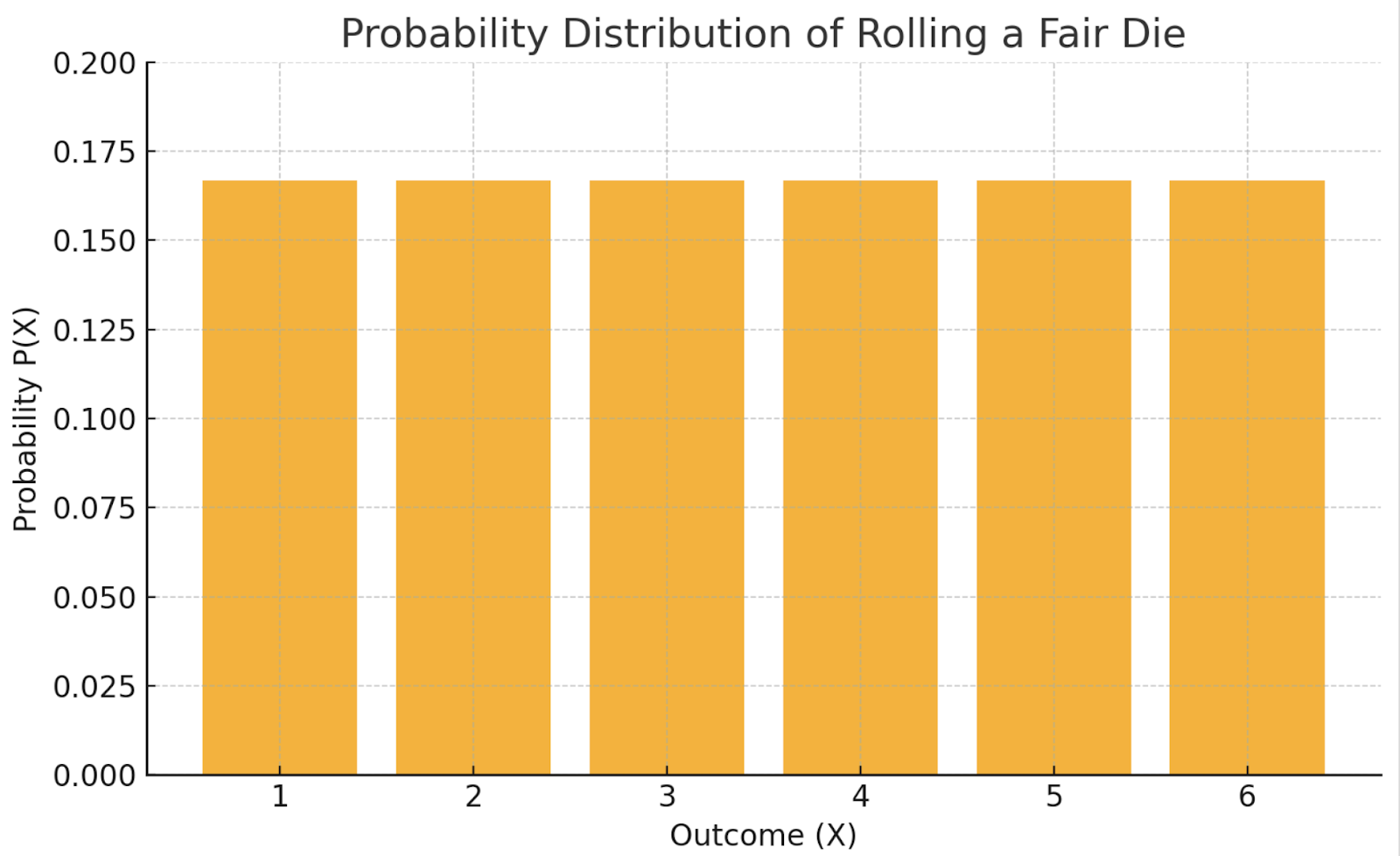
Esta PMF uniforme aparecería como un gráfico de barras planas, en el que todos los resultados son igual de probables.
Estas visualizaciones facilitan las cosas:
- Interpreta intuitivamente las distribuciones,
- Compara probabilidades relativas,
- Detecta distribuciones asimétricas o simétricas.
Aplicaciones de las funciones de masa de probabilidad
Los PMF se utilizan en varios ámbitos:
Estadísticas
Para calcular los valores esperados:
y desviaciones:
Aprendizaje automático
En los algoritmos de clasificación (por ejemplo, Naive Bayes), los PMF describen las probabilidades de las características categóricas. Los modelos probabilísticos, como los Modelos de Markov Ocultos, también dependen de los PMF para las transiciones de estado y las emisiones.
Ingeniería de fiabilidad
Los PMF ayudan a determinar la probabilidad de que un sistema o componente falle en un paso de tiempo concreto.
Economía y finanzas
Modelizar escenarios de mercado o resultados de inversión en los que el número de resultados es finito y distinto.
Inferencia bayesiana
Las PMF sirven como distribuciones a priori en los modelos bayesianos discretos. Cuando se observan nuevas pruebas, el PMF a priori se actualiza a un PMF a posteriori, lo que hace que la actualización bayesiana sea manejable para problemas discretos.
Si quieres aprender cómo funcionan las probabilidades condicionales,consulta nuestra página Probabilidad Condicional: Una mirada cercana tutorial.
Simulaciones Monte Carlo
Los PMF también son esenciales en las simulaciones de Montecarlo, especialmente para sistemas con resultados discretos y probabilísticos. Estas simulaciones utilizan el muestreo aleatorio de un PMF para estimar el comportamiento o rendimiento de un modelo a lo largo de muchas iteraciones.
Conclusión
La función de masa de probabilidad proporciona la estructura matemática para modelizar variables aleatorias discretas, a diferencia de las FDP, que tratan con variables continuas. Permiten un modelado potente en todos los ámbitos, desde lanzamientos básicos de monedas hasta complejos sistemas de machine learning.
Puntos clave:
- Los PMF no son negativos y suman 1 en todos los valores posibles.
- Definen la forma y las características de las distribuciones discretas de probabilidad.
- Las PMF son esenciales en diversas aplicaciones, desde la estadística clásica hasta la IA y las finanzas modernas.
- En la inferencia bayesiana y los métodos de Montecarlo, las PMF son fundamentales para actualizar las creencias y simular sistemas inciertos.
Para quienes profundicen en la teoría de la probabilidad, explorar las funciones de distribución acumulativa (FDA) y los cálculos del valor esperado enriquecerá aún más tu comprensión de cómo puede cuantificarse y aprovecharse la incertidumbre en la toma de decisiones. Explora nuestros cursos:

Transformadora de Datos y Estratega de IA | Conferenciante Internacional | Ética de la IA | Inventora | Mujer Logradora Global | Autora
Preguntas frecuentes del PMF
¿Qué es una función de masa de probabilidad?
A La PMF asigna probabilidades a resultados discretos de una variable aleatoria, asegurándose de que todos los valores suman 1.
¿En qué se diferencia un PMF de un PDF?
Una PMF se aplica a variables discretas, mientras que una PDF se aplica a variables continuas.
¿Puede ser negativo un PMF?
No, una PMF debe ser siempre no negativa.
¿Cuáles son las distribuciones habituales que utilizan PMF?
Algunos ejemplos son las distribuciones Bernoulli, Binomial, Geométrica y Poisson.
¿Cómo se utiliza un PMF en aplicaciones reales?
Las PMF se utilizan mucho en machine learning, finanzas, ingeniería de fiabilidad y modelización estadística.