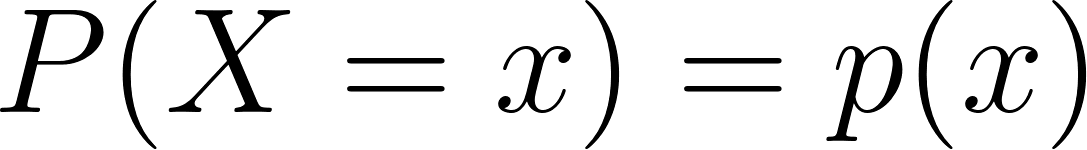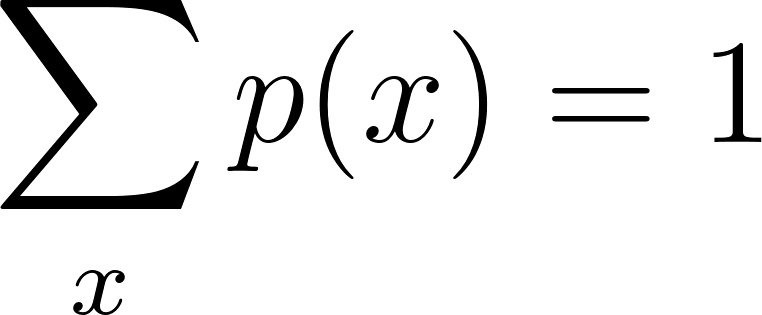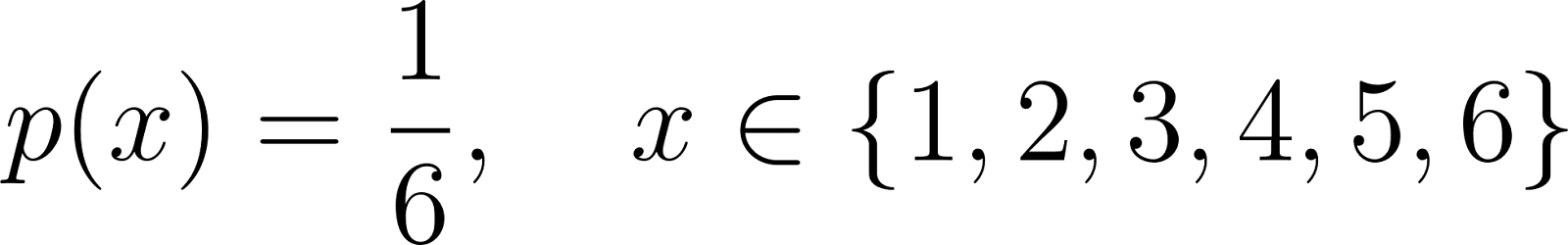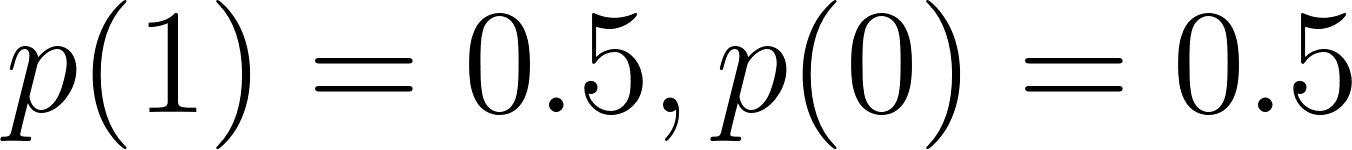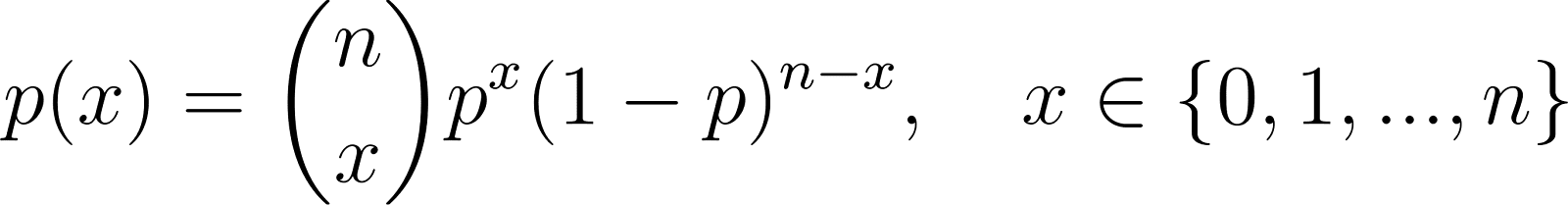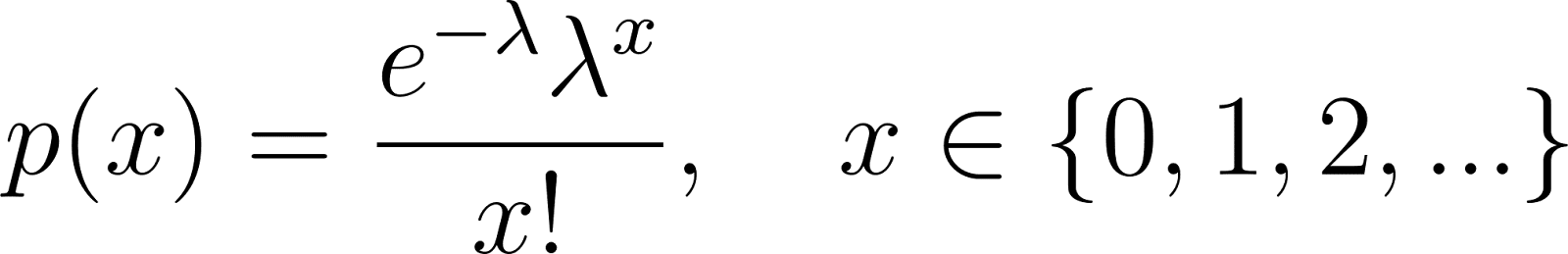Curso
Em probabilidade e estatística, a probabilidade de um resultado para variáveis aleatórias discretas é quantificada pela função de massa de probabilidade (PMF), enquanto que para variáveis contínuas, usamos a função de densidade de probabilidade (PDF).
Seja modelando lançamentos de moedas, falhas de equipamentos ou cliques de usuários em uma página da Web, o PMF nos ajuda a quantificar a probabilidade de resultados diferentes.
Entendendo a função de massa de probabilidade
A fórmula da função de massa de probabilidade
Matematicamente, a função de massa de probabilidade de uma variável aleatória discreta X é definida como:
Onde:
- X é uma variável aleatória discreta,
- x é um valor que X pode assumir,
- p(x) é a probabilidade de que X seja igual a x.
Duas condições críticas devem ser atendidas para um PMF válido:
1. Não negatividade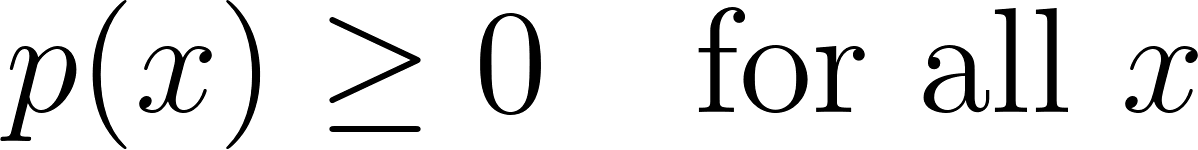
2. A probabilidade total deve ser igual a um
Essas condições garantem que todas as probabilidades atribuídas façam sentido lógico e matemático. O PMF fornece uma descrição completa da distribuição de X, possibilitando o cálculo de valores esperados, variâncias e outras medidas estatísticas.
Definição e principais propriedades
O PMF tem várias propriedades definidoras que o distinguem:
- Discrição: O PMF só se aplica a variáveis aleatórias discretas, aquelas que podem assumir valores contáveis (como 0, 1, 2, ...).
- Normalização: A soma do PMF em todos os valores possíveis de X deve ser exatamente 1.
- Atribuição de probabilidade individual: A cada valor possível x é atribuída uma probabilidade específica p(x), que capta a probabilidade desse resultado específico.
Por exemplo, o PMF para rolar um dado justo de seis lados é:
Aqui, cada valor de 1 a 6 tem a mesma chance de aparecer, e a soma de todas as probabilidades é 1.
Função de massa de probabilidade versus função de massa de probabilidade. Função de densidade de probabilidade
Vamos entender em detalhes as diferenças entre PMFs e PDFs e como eles modelam asdistribuições discretas econtínuas, respectivamente:
|
Característica |
PMF |
|
|
Tipo de variável |
Discreto |
Contínuo |
|
Valor de saída |
||
|
Regra de totalização |
Exemplo de PMF
Vejamos um exemplo clássico de PMF: jogar uma moeda justa (teste de Bernoulli):
Vamos realizar um teste de Bernoulli em Python para que você entenda isso melhor.
import matplotlib.pyplot as plt
from scipy.stats import bernoulli
# Parameters
p = 0.5 # Probability of Heads
# PMF for a fair coin
x = [0, 1] # 0 = Tails, 1 = Heads
pmf_values = bernoulli.pmf(x, p)
# Plotting
plt.bar(x, pmf_values, tick_label=['Tails (0)', 'Heads (1)'])
plt.title('PMF of a Fair Coin Toss (Bernoulli Trial)')
plt.ylabel('Probability')
plt.xlabel('Outcome')
plt.grid(axis='y', linestyle='--')
plt.show()
Exemplo em PDF
Aqui está um exemplo em PDF: medir a altura de uma pessoa (variável contínua).
O PDF pode mostrar que a densidade de probabilidade é maior em torno de 170 cm, mas a probabilidade de qualquer altura exata é tecnicamente 0.
Novamente, vamos entender isso com um exemplo de código.
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
# Parameters
mu = 170 # mean height
sigma = 10 # standard deviation
# Continuous range of heights
x = np.linspace(130, 210, 500)
pdf_values = norm.pdf(x, mu, sigma)
# Plotting
plt.plot(x, pdf_values, label='PDF')
plt.title('PDF of Human Height (Normal Distribution)')
plt.xlabel('Height (cm)')
plt.ylabel('Probability Density')
plt.grid(True)
plt.axvline(mu, color='red', linestyle='--', label='Mean (170 cm)')
plt.legend()
plt.show()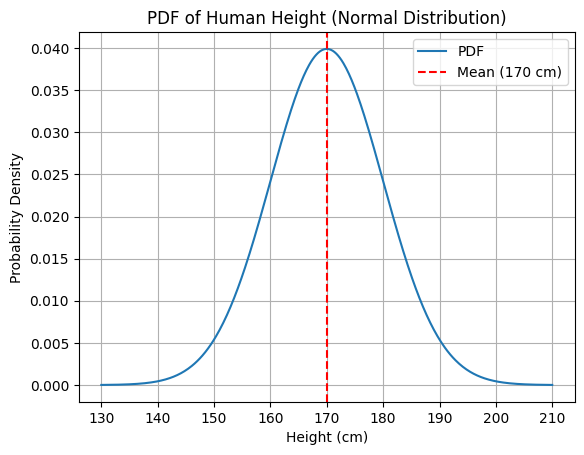
Enquanto os PMFs atribuem probabilidades reais a resultados específicos, os PDFs descrevem a probabilidade relativa de resultados em um intervalo.
Distribuições discretas comuns usando PMF
Exemplos comuns de distribuições de probabilidade discretas são as distribuições Bernoulli, binomial, geométrica e Poisson. Vamos dar uma olhada em cada um deles.
PMF da distribuição de Bernoulli
A distribuição de Bernoulli modela um único experimento com apenas dois resultados possíveis: sucesso (1) e fracasso (0).
Onde p é a probabilidade de sucesso.
Aqui está um exemplo: Jogar uma moeda justa em que o sucesso = cara:
PMF da distribuição binomial
A distribuição binomial generaliza a Bernoulli para várias tentativas:
Onde:
- n é o número de tentativas independentes,
- p é a probabilidade de sucesso em cada tentativa,
- x é o número de sucessos.
Um exemplo seria a contagem de itens com defeito em um lote de produtos.
PMF da distribuição geométrica
A distribuição geométrica é usada para modelar o número de falhas antes do primeiro sucesso em testes Bernoulli independentes e repetidos:
Um exemplo comum disso seria o número de lançamentos de moedas até que a primeira cabeça apareça.
PMF da distribuição de Poisson
A distribuição de Poisson modela o número de eventos em um intervalo fixo de tempo ou espaço:
Onde λ é o número esperado de eventos por intervalo.
Um exemplo disso é o número de chegadas de clientes em um centro de serviços por hora.
Visualização de funções de massa de probabilidade
Os PMFs são visualizados por meio de gráficos de barras, onde:
- O eixo x representa os valores possíveis da variável aleatória.
- O eixo y representa a probabilidade atribuída pelo PMF.
Aqui está uma tabela que mostra um exemplo: rolando um dado justo
|
X |
1 |
2 |
3 |
4 |
5 |
6 |
|
P(X) |
1/6 |
1/6 |
1/6 |
1/6 |
1/6 |
1/6 |
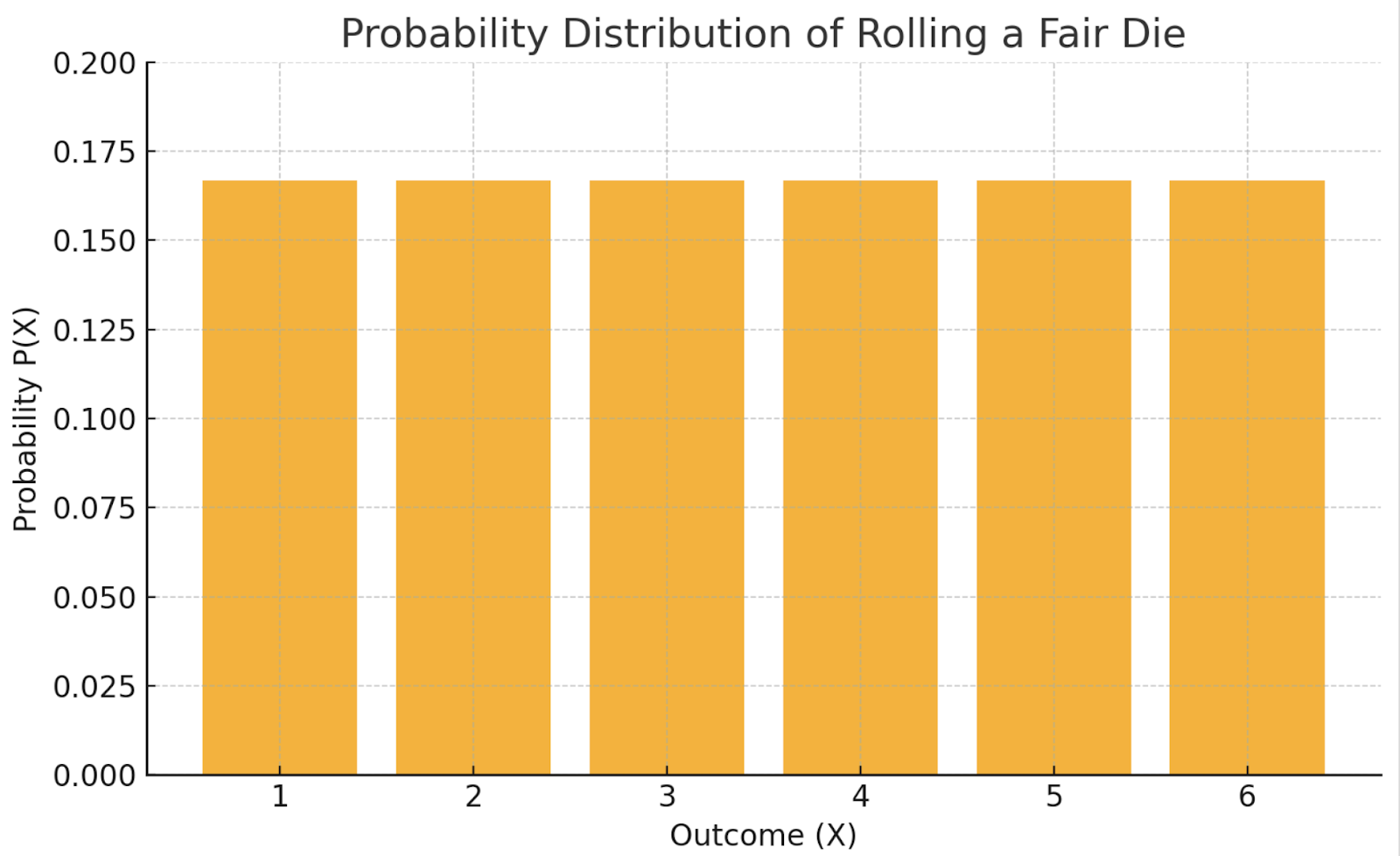
Esse PMF uniforme apareceria como um gráfico de barras plano, em que todos os resultados são igualmente prováveis.
Essas visualizações facilitam a visualização:
- Interprete as distribuições intuitivamente,
- Compare as probabilidades relativas,
- Distribuições simétricas ou distorcidas pontuais.
Aplicações de funções de massa de probabilidade
Os PMFs são usados em vários domínios:
Estatísticas
Para calcular os valores esperados:
e variações:
Machine learning
Nos algoritmos de classificação (por exemplo, Naive Bayes), os PMFs descrevem as probabilidades de recursos categóricos. Os modelos probabilísticos, como os modelos de Markov oculto, também dependem de PMFs para transições de estado e emissões.
Engenharia de confiabilidade
Os PMFs ajudam a determinar a probabilidade de falha de um sistema ou componente em uma etapa de tempo específica.
Economia e finanças
Modelagem de cenários de mercado ou resultados de investimentos em que o número de resultados é finito e distinto.
Inferência bayesiana
Os PMFs servem como distribuições prévias em modelos bayesianos discretos. Quando novas evidências são observadas, a PMF anterior é atualizada para uma PMF posterior, o que torna a atualização bayesiana viável para problemas discretos.
Se você quiser saber como funcionam as probabilidades condicionais,consulte o site Probabilidade condicional: Um olhar atento tutorial.
Simulações de Monte Carlo
Os PMFs também são essenciais nas simulações de Monte Carlo, especialmente para sistemas com resultados discretos e probabilísticos. Essas simulações usam amostragem aleatória de um PMF para estimar o comportamento ou o desempenho de um modelo em várias iterações.
Conclusão
A função de massa de probabilidade fornece a estrutura matemática para modelar variáveis aleatórias discretas, ao contrário das PDFs, que lidam com variáveis contínuas. Eles permitem uma modelagem avançada em vários domínios, desde lançamentos básicos de moedas até sistemas complexos de machine learning.
Principais conclusões:
- Os PMFs não são negativos e somam 1 em todos os valores possíveis.
- Eles definem a forma e as características das distribuições de probabilidade discretas.
- As PMFs são essenciais em várias aplicações, desde a estatística clássica até a IA e as finanças modernas.
- Na inferência bayesiana e nos métodos de Monte Carlo, os PMFs são fundamentais para atualizar crenças e simular sistemas incertos.
Para aqueles que estão se aprofundando na teoria da probabilidade, explorar as funções de distribuição cumulativa (CDFs) e os cálculos de valor esperado enriquecerá ainda mais sua compreensão de como a incerteza pode ser quantificada e aproveitada na tomada de decisões. Explore nossos cursos:

Transformador de dados e estrategista de IA | Palestrante internacional | Ético em IA | Inventor | Mulher de sucesso global | Autor
Perguntas frequentes sobre o PMF
O que é uma função de massa de probabilidade?
A O PMF atribui probabilidades a resultados discretos de uma variável aleatória, garantindo que todos os valores somem 1.
Qual é a diferença entre um PMF e um PDF?
Um PMF se aplica a variáveis discretas, enquanto um PDF se aplica a variáveis contínuas.
Um PMF pode ser negativo?
Não, um PMF deve ser sempre não negativo.
Quais são as distribuições comuns que usam PMFs?
Os exemplos incluem as distribuições Bernoulli, Binomial, Geométrica e Poisson.
Como um PMF é usado em aplicativos do mundo real?
Os PMFs são amplamente usados em machine learning, finanças, engenharia de confiabilidade e modelagem estatística.