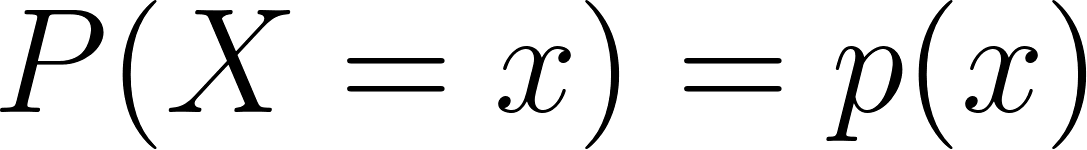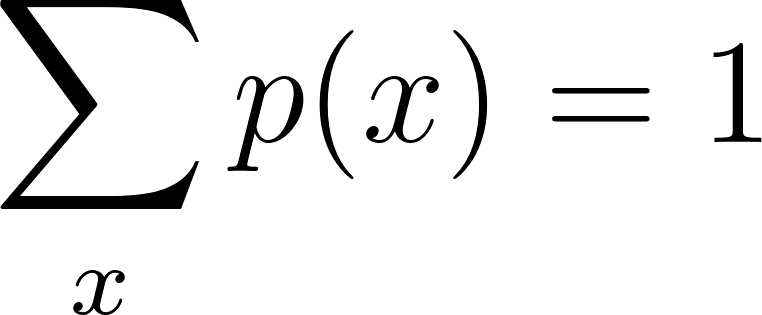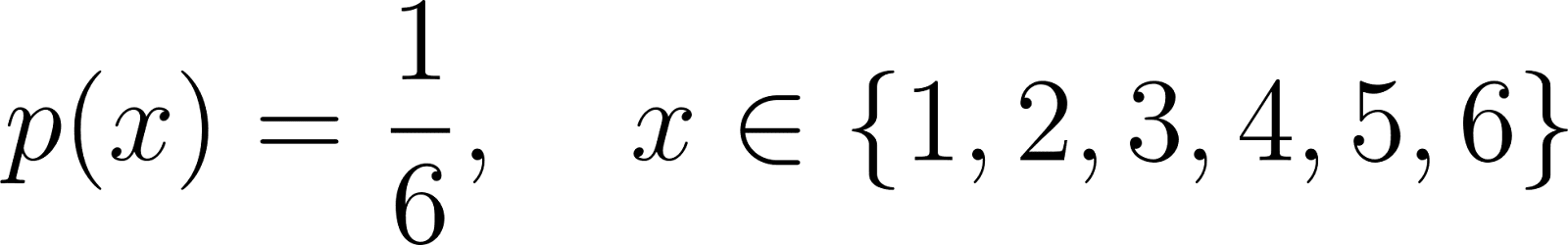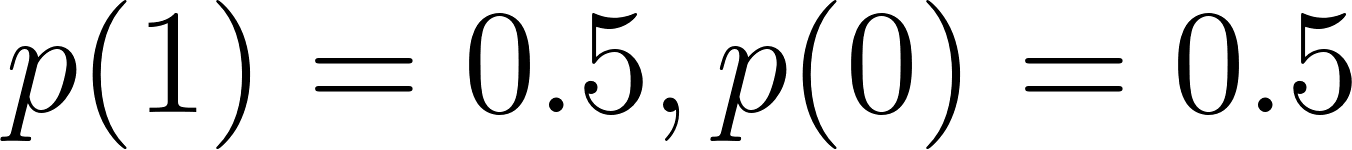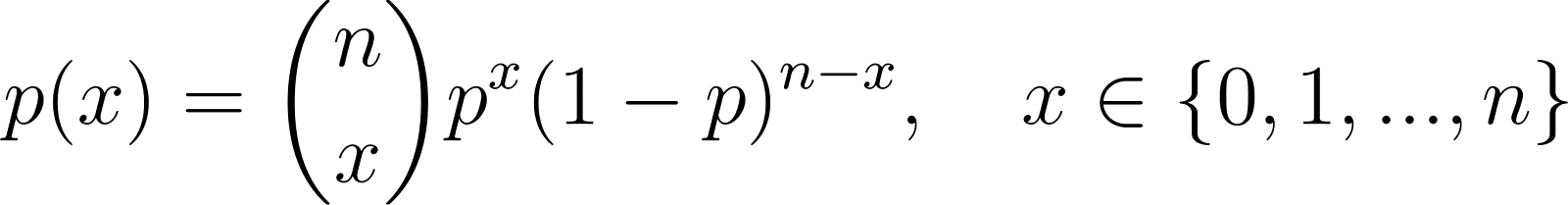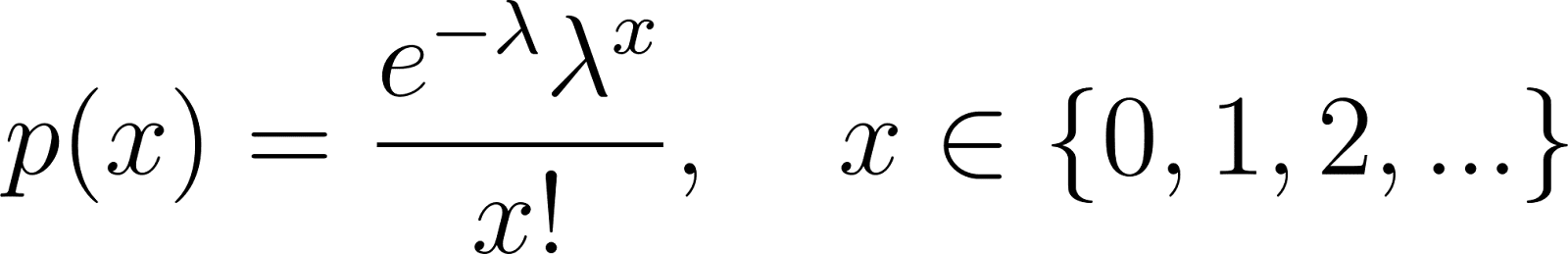Course
In probability and statistics, the likelihood of an outcome for discrete random variables is quantified by the probability mass function (PMF), whereas for continuous variables, we use the probability density function (PDF).
Whether modeling coin flips, equipment failures, or user clicks on a webpage, the PMF helps us quantify the likelihood of different outcomes.
Understanding the Probability Mass Function
The probability mass function formula
Mathematically, the probability mass function of a discrete random variable X is defined as:
Where:
- X is a discrete random variable,
- x is a value that X can take,
- p(x) is the probability that X equals x.
Two critical conditions must be met for a valid PMF:
1. Non-negativity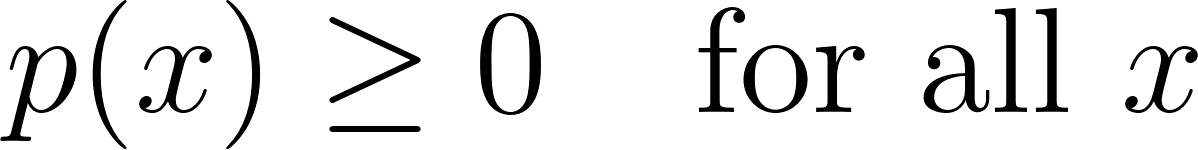
2. Total probability must equal one
These conditions ensure that all assigned probabilities make logical and mathematical sense. The PMF provides a complete description of the distribution of X, making it possible to compute expected values, variances, and other statistical measures.
Definition and key properties
The PMF has several defining properties that distinguish it:
- Discreteness: The PMF only applies to discrete random variables, those that can take on countable values (like 0, 1, 2, ...).
- Normalization: The sum of the PMF over all possible values of X must be exactly 1.
- Individual probability assignment: Each possible value x is assigned a specific probability p(x), which captures how likely that particular outcome is.
For example, the PMF for rolling a fair six-sided die is:
Here, each value from 1 to 6 has an equal chance of appearing, and the sum of all probabilities is 1.
Probability Mass Function vs. Probability Density Function
Let’s understand in detail the differences between PMFs and PDFs and how they model the discrete and continuous distributions, respectively:
|
Characteristic |
PMF |
|
|
Variable Type |
Discrete |
Continuous |
|
Value Output |
||
|
Summation Rule |
PMF example
Let’s take a classic PMF example: tossing a fair coin (Bernoulli trial):
Let’s perform a Bernoulli trial in Python to understand this better.
import matplotlib.pyplot as plt
from scipy.stats import bernoulli
# Parameters
p = 0.5 # Probability of Heads
# PMF for a fair coin
x = [0, 1] # 0 = Tails, 1 = Heads
pmf_values = bernoulli.pmf(x, p)
# Plotting
plt.bar(x, pmf_values, tick_label=['Tails (0)', 'Heads (1)'])
plt.title('PMF of a Fair Coin Toss (Bernoulli Trial)')
plt.ylabel('Probability')
plt.xlabel('Outcome')
plt.grid(axis='y', linestyle='--')
plt.show()
PDF example
Here’s a PDF example: measuring a person’s height (continuous variable).
The PDF might show that the probability density is highest around 170 cm, but the probability of any exact height is technically 0.
Again, let’s understand this with a code example.
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
# Parameters
mu = 170 # mean height
sigma = 10 # standard deviation
# Continuous range of heights
x = np.linspace(130, 210, 500)
pdf_values = norm.pdf(x, mu, sigma)
# Plotting
plt.plot(x, pdf_values, label='PDF')
plt.title('PDF of Human Height (Normal Distribution)')
plt.xlabel('Height (cm)')
plt.ylabel('Probability Density')
plt.grid(True)
plt.axvline(mu, color='red', linestyle='--', label='Mean (170 cm)')
plt.legend()
plt.show()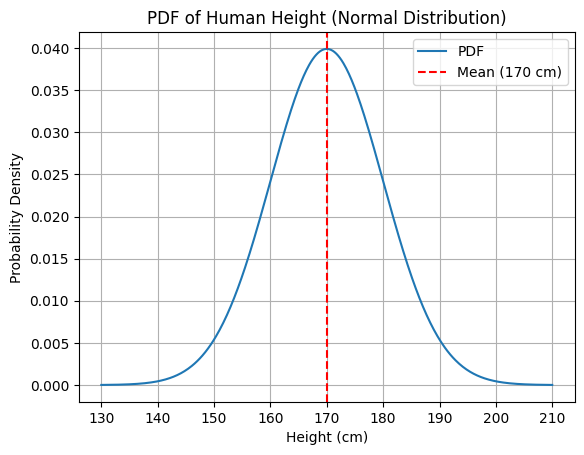
While PMFs assign actual probabilities to specific outcomes, PDFs describe the relative likelihood of outcomes within an interval.
Common Discrete Distributions Using PMF
Common examples of discrete probability distributions are the Bernoulli, binomial, geometric, and Poisson distributions. Let's take a look at each.
PMF of the Bernoulli distribution
The Bernoulli distribution models a single experiment with only two possible outcomes: success (1) and failure (0).
Where p is the probability of success.
Here is an example: Tossing a fair coin where success = heads:
PMF of the binomial distribution
The Binomial distribution generalizes the Bernoulli to multiple trials:
Where:
- n is the number of independent trials,
- p is the probability of success in each trial,
- x is the number of successes.
One example would be counting defective items in a batch of products.
PMF of the Geometric distribution
The Geometric distribution is used to model the number of failures before the first success in repeated independent Bernoulli trials:
One common example of this would be the number of coin flips until the first head appears.
PMF of the Poisson distribution
The Poisson distribution models the number of events in a fixed interval of time or space:
Where λ is the expected number of events per interval.
An example of this is the number of customer arrivals at a service center per hour.
Visualizing Probability Mass Functions
PMFs are visualized using bar charts, where:
- The x-axis represents the possible values of the random variable.
- The y-axis represents the probability assigned by the PMF.
Here is a table showing an example: rolling a fair die
|
X |
1 |
2 |
3 |
4 |
5 |
6 |
|
P(X) |
1/6 |
1/6 |
1/6 |
1/6 |
1/6 |
1/6 |
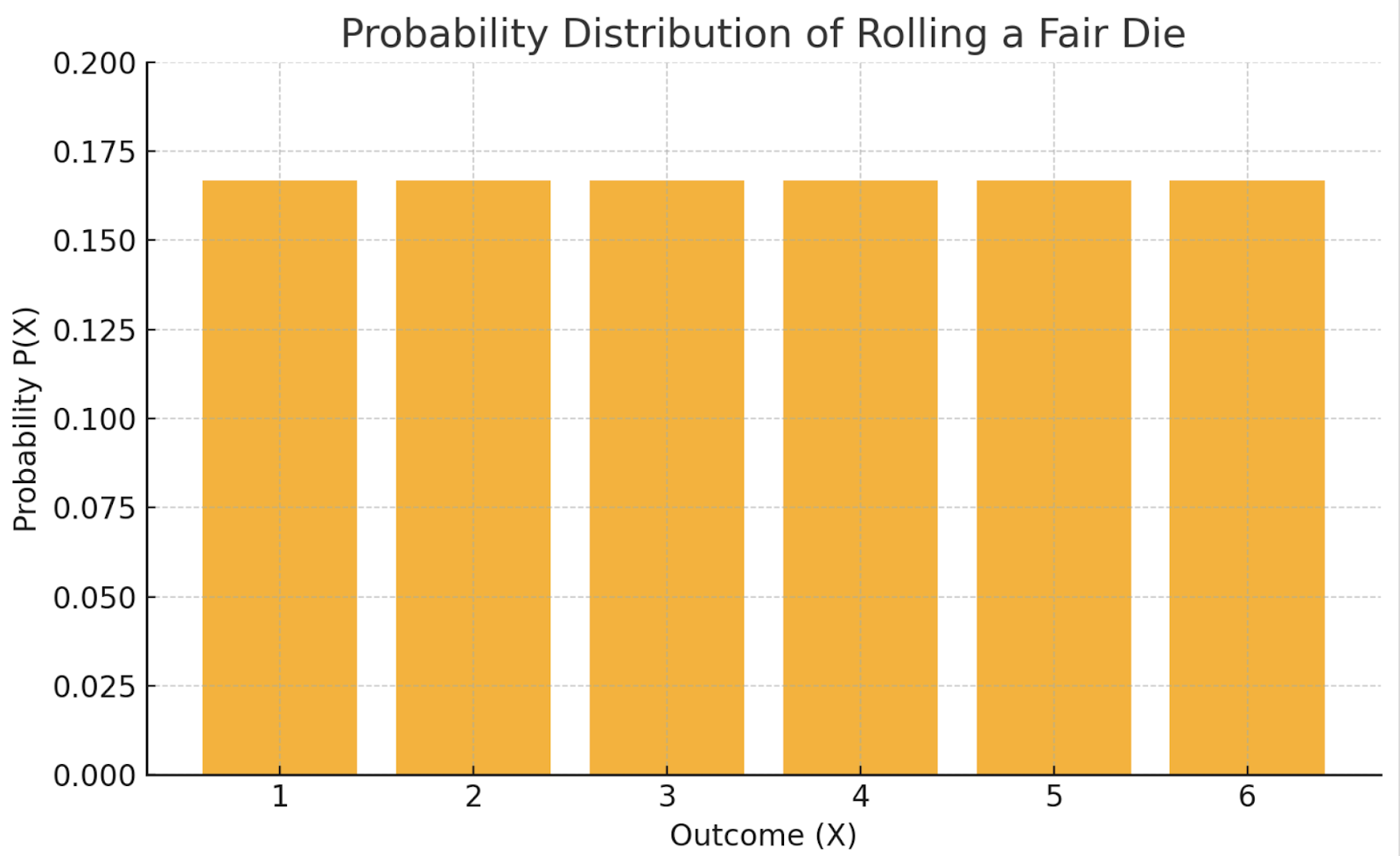
This uniform PMF would appear as a flat bar chart, where all outcomes are equally likely.
Such visualizations make it easier to:
- Interpret distributions intuitively,
- Compare relative probabilities,
- Spot skewed or symmetric distributions.
Applications of Probability Mass Functions
PMFs are used across various domains:
Statistics
For calculating expected values:
and variances:
Machine learning
In classification algorithms (e.g., Naive Bayes), PMFs describe the likelihoods of categorical features. Probabilistic models like Hidden Markov Models also depend on PMFs for state transitions and emissions.
Reliability engineering
PMFs help determine the probability of a system or component failing at a specific time step.
Economics and finance
Modeling market scenarios or investment outcomes where the number of outcomes is finite and distinct.
Bayesian inference
PMFs serve as prior distributions in discrete Bayesian models. When new evidence is observed, the prior PMF is updated to a posterior PMF, making Bayesian updating tractable for discrete problems.
If you want to learn about how conditional probabilities work, check out our Conditional Probability: A Close Look tutorial.
Monte Carlo Simulations
PMFs are also essential in Monte Carlo simulations, especially for systems with discrete and probabilistic outcomes. These simulations use random sampling from a PMF to estimate a model's behavior or performance over many iterations.
Conclusion
The probability mass function provides the mathematical structure for modeling discrete random variables, unlike PDFs, which deal with continuous variables. They enable powerful modeling across domains, from basic coin tosses to complex machine learning systems.
Key takeaways:
- PMFs are non-negative and sum to 1 across all possible values.
- They define the shape and characteristics of discrete probability distributions.
- PMFs are essential in various applications, from classical statistics to modern AI and finance.
- In Bayesian inference and Monte Carlo methods, PMFs are central to updating beliefs and simulating uncertain systems.
For those diving deeper into probability theory, exploring cumulative distribution functions (CDFs) and expected value calculations will further enrich your understanding of how uncertainty can be quantified and leveraged in decision-making. Explore our courses:

I am an AI Strategist and Ethicist working at the intersection of data science, product, and engineering to build scalable machine learning systems. Listed as one of the "Top 200 Business and Technology Innovators" in the world, I am on a mission to democratize machine learning and break the jargon for everyone to be a part of this transformation.
PMF FAQs
What is a probability mass function?
A PMF assigns probabilities to discrete outcomes of a random variable, ensuring all values sum to 1.
How does a PMF differ from a PDF?
A PMF applies to discrete variables, while a PDF applies to continuous variables.
Can a PMF be negative?
No, a PMF must always be non-negative.
What are common distributions that use PMFs?
Examples include the Bernoulli, Binomial, Geometric, and Poisson distributions.
How is a PMF used in real-world applications?
PMFs are widely used in machine learning, finance, reliability engineering, and statistical modeling.