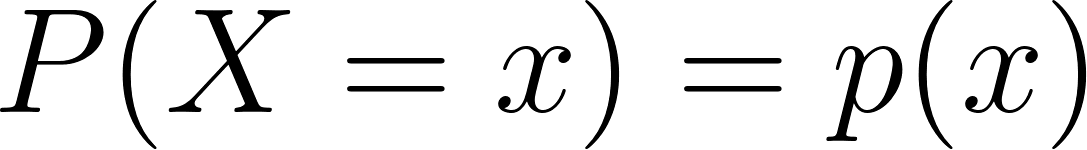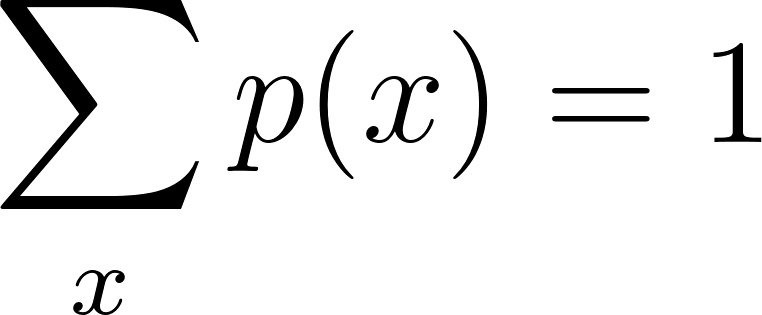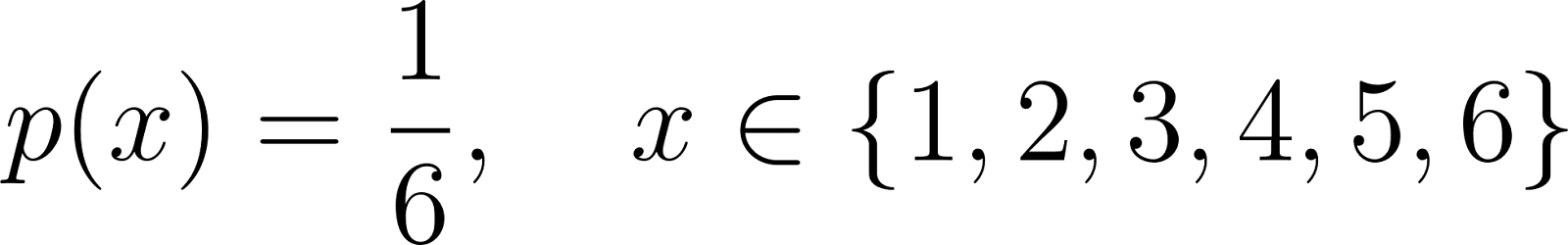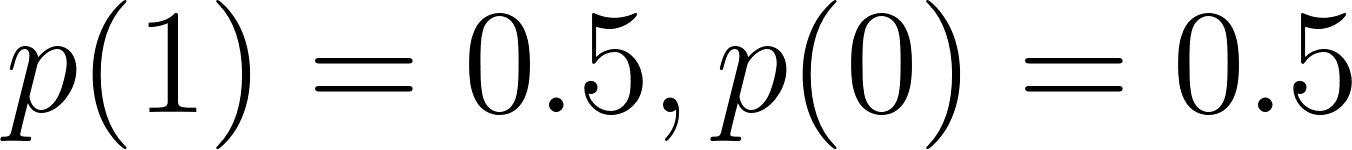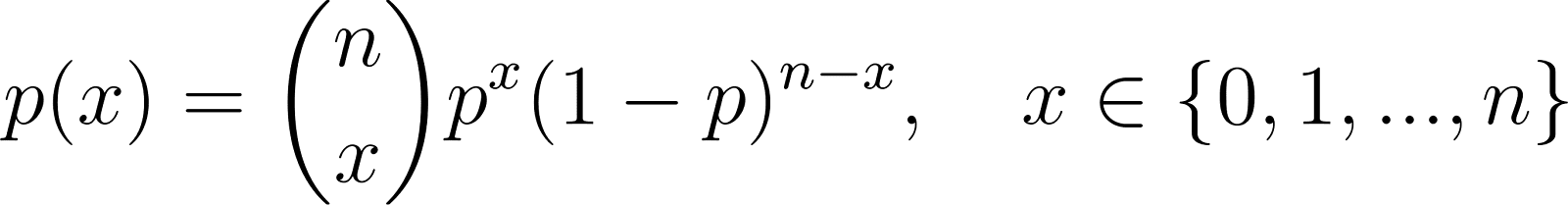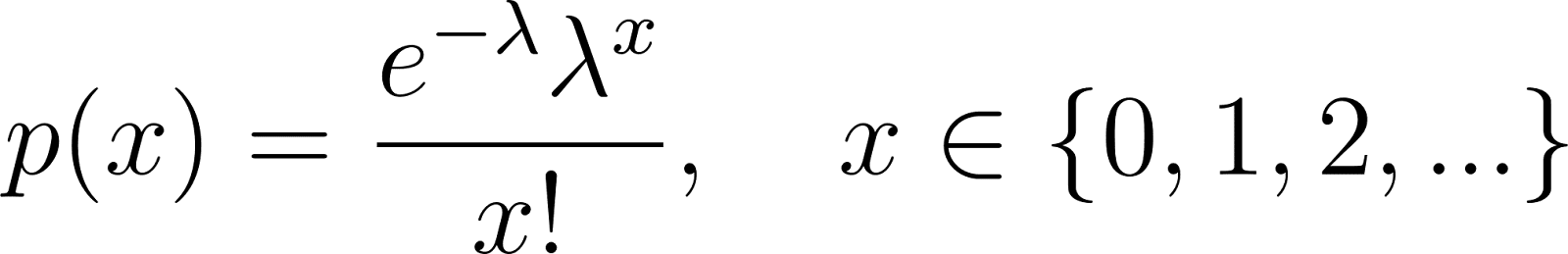Kurs
In der Probabilistik & Statistik wird die Wahrscheinlichkeit eines Ergebnisses für diskrete Zufallsvariablen durch die Wahrscheinlichkeitsmassenfunktion (PMF) quantifiziert, während wir für kontinuierliche Variablen die Wahrscheinlichkeitsdichtefunktion (PDF) verwenden.
Ob wir nun Münzwürfe, Geräteausfälle oder Klicks auf eine Webseite modellieren, die PMF hilft uns, die Wahrscheinlichkeit verschiedener Ergebnisse zu quantifizieren.
Die Wahrscheinlichkeits-Masse-Funktion verstehen
Die Formel für die Wahrscheinlichkeits-Massenfunktion
Mathematisch gesehen ist die Wahrscheinlichkeits-Massenfunktion einer diskreten Zufallsvariablen X ist definiert als:
Wo:
- X ist eine diskrete Zufallsvariable,
- x ist ein Wert, den X annehmen kann,
- p(x) ist die Wahrscheinlichkeit, dass X gleich x ist.
Für einen gültigen PMF müssen zwei wichtige Bedingungen erfüllt sein:
1. Nicht-Negativität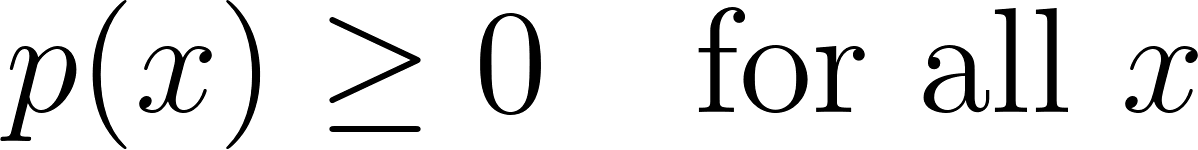
2. Die Gesamtwahrscheinlichkeit muss gleich eins sein
Diese Bedingungen stellen sicher, dass alle zugewiesenen Wahrscheinlichkeiten logisch und mathematisch sinnvoll sind. Die PMF liefert eine vollständige Beschreibung der Verteilung von X und ermöglicht es, Erwartungswerte, Varianzen und andere statistische Maße zu berechnen.
Definition und wichtigste Eigenschaften
Das PMF hat mehrere Eigenschaften, die es auszeichnen:
- Diskretion: Die PMF gilt nur für diskrete Zufallsvariablen, also solche, die abzählbare Werte annehmen können (wie 0, 1, 2, ...).
- Normalisierung: Die Summe der PMF über alle möglichen Werte von X muss genau 1 sein.
- Individuelle Wahrscheinlichkeitszuweisung: Jedem möglichen Wert x wird eine bestimmte Wahrscheinlichkeit p(x) zugeordnet , die angibt, wie wahrscheinlich das jeweilige Ergebnis ist.
Die PMF für einen fairen sechsseitigen Würfel ist zum Beispiel:
Hier hat jeder Wert von 1 bis 6 die gleiche Chance, aufzutreten, und die Summe aller Wahrscheinlichkeiten ist 1.
Wahrscheinlichkeits-Masse-Funktion vs. Wahrscheinlichkeitsdichtefunktion
Wir wollen die Unterschiede zwischen PMFs und PDFs im Detail verstehen und wie sie die diskreten bzw.kontinuierlichen Verteilungen modellieren:
|
Charakteristisch |
PMF |
|
|
Variable Art |
Diskret |
Kontinuierlich |
|
Wert Ausgabe |
||
|
Summierungsregel |
PMF-Beispiel
Nehmen wir ein klassisches PMF-Beispiel: das Werfen einer fairen Münze (Bernoulli-Versuch):
Um das besser zu verstehen, führen wir einen Bernoulli-Versuch in Python durch.
import matplotlib.pyplot as plt
from scipy.stats import bernoulli
# Parameters
p = 0.5 # Probability of Heads
# PMF for a fair coin
x = [0, 1] # 0 = Tails, 1 = Heads
pmf_values = bernoulli.pmf(x, p)
# Plotting
plt.bar(x, pmf_values, tick_label=['Tails (0)', 'Heads (1)'])
plt.title('PMF of a Fair Coin Toss (Bernoulli Trial)')
plt.ylabel('Probability')
plt.xlabel('Outcome')
plt.grid(axis='y', linestyle='--')
plt.show()
PDF-Beispiel
Hier ein PDF-Beispiel: Messung der Körpergröße einer Person (kontinuierliche Variable).
Die PDF könnte zeigen, dass die Wahrscheinlichkeitsdichte bei 170 cm am höchsten ist, aber die Wahrscheinlichkeit für eine exakte Höhe ist technisch gesehen 0.
Lass uns das noch einmal anhand eines Code-Beispiels verstehen.
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
# Parameters
mu = 170 # mean height
sigma = 10 # standard deviation
# Continuous range of heights
x = np.linspace(130, 210, 500)
pdf_values = norm.pdf(x, mu, sigma)
# Plotting
plt.plot(x, pdf_values, label='PDF')
plt.title('PDF of Human Height (Normal Distribution)')
plt.xlabel('Height (cm)')
plt.ylabel('Probability Density')
plt.grid(True)
plt.axvline(mu, color='red', linestyle='--', label='Mean (170 cm)')
plt.legend()
plt.show()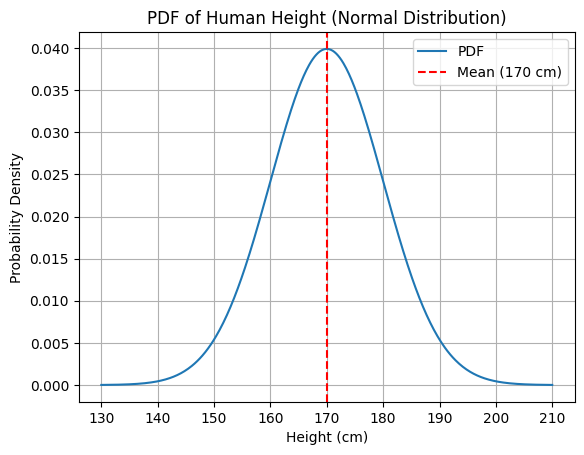
Während PMFs bestimmten Ergebnissen tatsächliche Wahrscheinlichkeiten zuordnen, beschreiben PDFs die relative Wahrscheinlichkeit von Ergebnissen innerhalb eines Intervalls.
Allgemeine diskrete Verteilungen mit PMF
Gängige Beispiele für diskrete Wahrscheinlichkeitsverteilungen sind die Bernoulli-, Binomial-, geometrische und Poisson-Verteilung. Schauen wir uns beide an.
PMF der Bernoulli-Verteilung
Die Bernoulli-Verteilung modelliert ein einzelnes Experiment mit nur zwei möglichen Ergebnissen: Erfolg (1) und Misserfolg (0).
Wo p die Erfolgswahrscheinlichkeit ist.
Hier ist ein Beispiel: Das Werfen einer fairen Münze, bei der Erfolg = Kopf ist:
PMF der Binomialverteilung
Die Binomialverteilung verallgemeinert die Bernoulli-Verteilung auf mehrere Versuche:
Wo:
- n ist die Anzahl der unabhängigen Versuche,
- p ist die Erfolgswahrscheinlichkeit in jedem Versuch,
- x ist die Anzahl der Erfolge.
Ein Beispiel wäre das Zählen von fehlerhaften Artikeln in einer Charge von Produkten.
PMF der Geometrischen Verteilung
Die geometrische Verteilung wird verwendet, um die Anzahl der Fehlschläge vor dem ersten Erfolg in wiederholten unabhängigen Bernoulli-Versuchen zu modellieren:
Ein gängiges Beispiel dafür wäre die Anzahl der Münzwürfe, bis der erste Kopf erscheint.
PMF der Poisson-Verteilung
Die Poisson-Verteilung modelliert die Anzahl der Ereignisse in einem festen Zeit- oder Raumintervall:
Dabei ist λ die erwartete Anzahl von Ereignissen pro Intervall.
Ein Beispiel dafür ist die Anzahl der Kundenankünfte in einem Servicecenter pro Stunde.
Visualisierung von Wahrscheinlichkeits-Masse-Funktionen
PMFs werden mit Hilfe von Balkendiagrammen visualisiert, wobei:
- Die x-Achse stellt die möglichen Werte der Zufallsvariablen dar.
- Die y-Achse stellt die vom PMF zugewiesene Wahrscheinlichkeit dar.
Hier ist eine Tabelle mit einem Beispiel: Würfeln mit einem fairen Würfel
|
X |
1 |
2 |
3 |
4 |
5 |
6 |
|
P(X) |
1/6 |
1/6 |
1/6 |
1/6 |
1/6 |
1/6 |
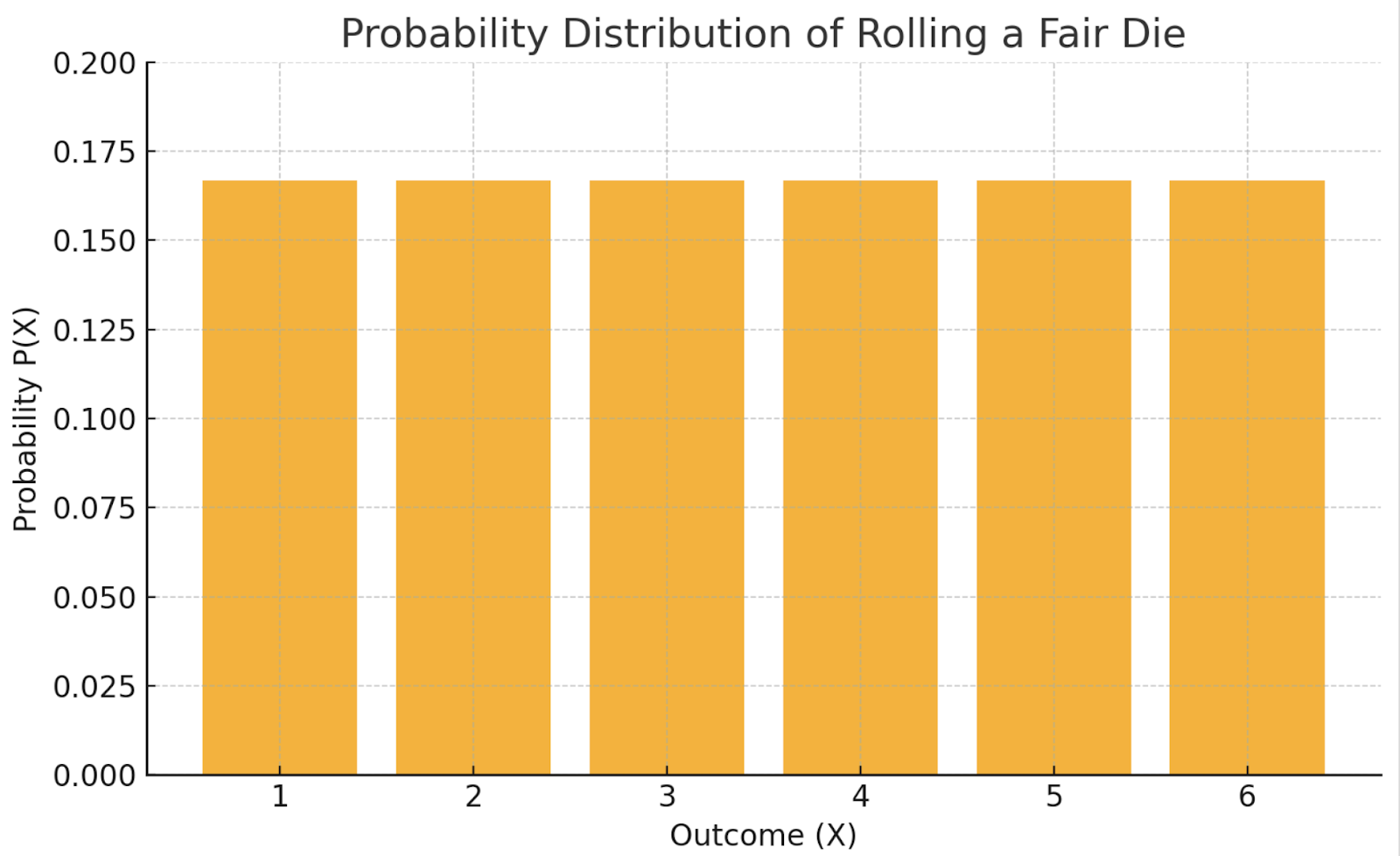
Dieses einheitliche PMF würde als flaches Balkendiagramm erscheinen, bei dem alle Ergebnisse gleich wahrscheinlich sind.
Solche Visualisierungen machen es einfacher,:
- Interpretiere Verteilungen intuitiv,
- Vergleiche relative Wahrscheinlichkeiten,
- Erkenne schiefe oder symmetrische Verteilungen.
Anwendungen von Wahrscheinlichkeits-Masse-Funktionen
PMFs werden in verschiedenen Bereichen eingesetzt:
Statistik
Zur Berechnung der erwarteten Werte:
und Abweichungen:
Maschinelles Lernen
In Klassifizierungsalgorithmen (z. B. Naive Bayes) beschreiben PMFs die Wahrscheinlichkeiten von kategorialen Merkmalen. Probabilistische Modelle wie Hidden Markov Models sind ebenfalls auf PMFs für Zustandsübergänge und Emissionen angewiesen.
Zuverlässigkeitstechnik
PMFs helfen dabei, die Wahrscheinlichkeit zu bestimmen, dass ein System oder eine Komponente zu einem bestimmten Zeitschritt ausfällt.
Wirtschaft und Finanzen
Modellierung von Marktszenarien oder Investitionsergebnissen, bei denen die Anzahl der Ergebnisse endlich und eindeutig ist.
Bayes'sche Inferenz
PMFs dienen als Prioritätsverteilungen in diskreten Bayes'schen Modellen. Wenn neue Beweise beobachtet werden, wird die prior PMF zu einer posterior PMF aktualisiert, was die Bayes'sche Aktualisierung für diskrete Probleme nachvollziehbar macht.
Wenn du wissen willst, wie bedingte Wahrscheinlichkeiten funktionieren, sieh dirunsere Bedingte Wahrscheinlichkeit an: A Close Look tutorial.
Monte-Carlo-Simulationen
PMFs sind auch bei Monte-Carlo-Simulationen unverzichtbar, insbesondere für Systeme mit diskreten und probabilistischen Ergebnissen. Diese Simulationen verwenden Zufallsstichproben aus einem PMF, um das Verhalten oder die Leistung eines Modells über viele Iterationen hinweg zu schätzen.
Fazit
Die Wahrscheinlichkeitsmassenfunktion bietet die mathematische Struktur für die Modellierung diskreter Zufallsvariablen, im Gegensatz zu PDFs, die sich mit kontinuierlichen Variablen befassen. Sie ermöglichen eine leistungsstarke Modellierung in allen Bereichen, von einfachen Münzwürfen bis hin zu komplexen maschinellen Lernsystemen.
Die wichtigsten Erkenntnisse:
- PMFs sind nicht-negativ und summieren sich über alle möglichen Werte zu 1.
- Sie definieren die Form und die Eigenschaften von diskreten Wahrscheinlichkeitsverteilungen.
- PMFs sind in verschiedenen Anwendungen unverzichtbar, von der klassischen Statistik bis hin zu moderner KI und Finanzen.
- In Bayes'schen Schlussfolgerungen und Monte-Carlo-Methoden spielen PMFs eine zentrale Rolle bei der Aktualisierung von Überzeugungen und der Simulation unsicherer Systeme.
Diejenigen, die tiefer in die Wahrscheinlichkeitstheorie eintauchen wollen, können sich mit kumulativen Verteilungsfunktionen (CDFs) und Erwartungswertberechnungen beschäftigen, um besser zu verstehen, wie Unsicherheiten quantifiziert und für die Entscheidungsfindung genutzt werden können. Entdecke unsere Kurse:

Ich bin KI-Stratege und Ethiker und arbeite an der Schnittstelle von Datenwissenschaft, Produkt und Technik, um skalierbare maschinelle Lernsysteme zu entwickeln. Als einer der "Top 200 Business and Technology Innovators" der Welt bin ich auf der Mission, das maschinelle Lernen zu demokratisieren und den Fachjargon zu überwinden, damit jeder an diesem Wandel teilhaben kann.
PMF-FAQs
Was ist eine Wahrscheinlichkeits-Massenfunktion?
A PMF ordnet diskreten Ergebnissen einer Zufallsvariablen Wahrscheinlichkeiten zu und stellt sicher, dass alle Werte die Summe 1 ergeben.
Wie unterscheidet sich ein PMF von einer PDF-Datei?
Eine PMF gilt für diskrete Variablen, während eine PDF für kontinuierliche Variablen gilt.
Kann ein PMF negativ sein?
Nein, eine PMF muss immer nicht-negativ sein.
Was sind gängige Verteilungen, die PMFs verwenden?
Beispiele sind die Bernoulli-, Binomial-, Geometrie- und Poisson-Verteilung.
Wie wird ein PMF in der Praxis eingesetzt?
PMFs werden häufig in den Bereichen maschinelles Lernen, Finanzen, Zuverlässigkeitstechnik und statistische Modellierung eingesetzt.