Explication de la forme échelonnée en ligne : Guide pour la transformation des matrices

Si vous avez commencé à étudier l'algèbre linéaire pour la science des données, vous avez probablement entendu parler assez souvent de la « forme échelonnée ».

La forme échelonnée (REF) est une forme de matrice qui aide à résoudre un système d'équations linéaires. En transformant une matrice sous cette forme particulière, nous pouvons déterminer si un système a des solutions, trouver ces solutions et comprendre la structure du système linéaire.

Dans cet article, nous explorerons ce qu'est la forme échelonnée et en quoi elle diffère de la forme échelonnée réduite. Nous présenterons également le processus étape par étape de la transformation des matrices à l'aide d'opérations élémentaires sur les lignes, nous apprendrons à résoudre des systèmes linéaires à l'aide de la substitution arrière et nous explorerons des techniques et des concepts avancés liés à la forme échelonnée. 

Concepts clés derrière la forme échelonnée par rangées

Comprenons ce qu'est la forme échelonnée et les concepts clés qui l'entourent.

Qu'est-ce que la forme échelonnée par rangs ?

Une matrice est sous forme échelonnée par rangs lorsqu'elle satisfait trois conditions essentielles :

1. Toutes les lignes composées uniquement de zéros se trouvent au bas de la matrice.
2. L'entrée principale (premier élément non nul) de chaque ligne non nulle apparaît à droite de l'entrée principale de la ligne située au-dessus.
3. Toutes les entrées d'une colonne situées sous une entrée principale sont des zéros.

Cela crée un motif en « escalier » où les entrées principales (appelées pivots) descendent de gauche à droite. 

Par exemple, cette matrice est sous forme échelonnée par rangs :

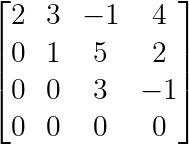
Forme échelonnée par rangées. (Image par l'auteur)

Comme nous le voyons ci-dessus, les pivots (2, 1 et 3) créent un motif en escalier, les zéros remplissant l'espace sous chaque pivot. Cette structure facilite la résolution des systèmes par substitution (comme nous le verrons plus tard).

Forme échelonnée réduite (RREF)

La forme échelonnée réduite approfondit ce concept en ajoutant deux exigences supplémentaires :

1. Chaque entrée principale doit être 1
2. Chaque 1 en tête est la seule entrée non nulle dans sa colonne.

Voici le même système ci-dessus, après transformation en RREF :

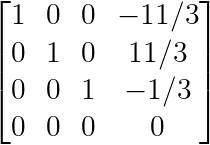
Forme échelonnée réduite. (Image par l'auteur)

Bien qu'un système puisse présenter plusieurs formes échelonnées, la forme échelonnée réduite est unique. 

Cette particularité rend la forme RREF utile pour identifier la structure des ensembles de solutions, mais les étapes de calcul supplémentaires nécessaires pour obtenir la forme RREF signifient que la forme échelonnée régulière combinée à la substitution arrière est souvent plus efficace pour résoudre des systèmes.

Opérations élémentaires sur les lignes pour former la forme échelonnée

Il existe trois types d'opérations élémentaires sur les lignes qui préservent l'ensemble des solutions tout en transformant les matrices.

Échange de lignes

Échange de lignes échange deux lignes, ce qui est utile lorsque nous devons positionner un élément non nul comme pivot :

R₁ ↔ R₂

Mise à l'échelle des lignes

Mise à l'échelle des lignes multiplie tous les éléments d'une ligne par une constante non nulle, ce qui permet de normaliser les valeurs pivots :

R₁ → cR₁ (where c ≠ 0)

Ajout d'une ligne

Ajout de lignes remplace une ligne par la somme d'elle-même et d'un multiple d'une autre ligne, ce qui est utile pour créer des zéros sous les pivots :

R₂ → R₂ + cR₁

Ces opérations constituent les éléments fondamentaux de l'élimination gaussienne, l'algorithme qui nous permet detransformer systématiquement n'importe quelle matrice en forme échelonnée tout en conservant le même ensemble de solutions.

Comment transformer une matrice en forme échelonnée par rangées

Examinons un exemple étape par étape, dans lequel nous prenons d'abord un système linéaire et le réduisons à la forme échelonnée.

Considérons le système :

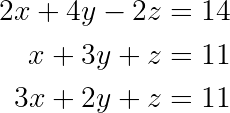
Système d'équations linéaires. (Image par l'auteur)

Étape 1 : Écrivez la matrice augmentée.

Tout d'abord, nous créons la matrice augmentée en combinant la matrice des coefficients avec les constantes :

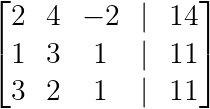
Création de la matrice augmentée (Image par l'auteur)

Étape 2 : Créer le premier pivot

Nous souhaitons que l'élément supérieur gauche soit notre premier pivot. Bien que nous puissions travailler avec 2, échanger les lignes pour obtenir 1 comme pivot simplifie les calculs :

R₁ ↔ R₂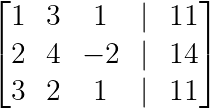

Création du premier pivot (Image par l'auteur)

Étape 3 : Éliminer sous le premier pivot

Nous créons maintenant des zéros sous le premier pivot en soustrayant les multiples appropriés de la ligne 1 :

R₂ → R₂ - 2R₁
R₃ → R₃ - 3R₁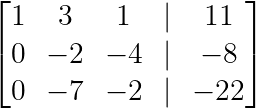

Éliminer en dessous du premier pivot. (Image par l'auteur)

Étape 4 : Créer le deuxième pivot

En passant à la deuxième colonne, nous pouvons simplifier en mettant à l'échelle la ligne 2 :

R₂ → -½R₂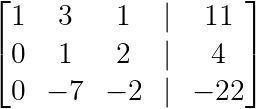

Création du deuxième pivot. (Image par l'auteur)

Étape 5 : Éliminer sous le deuxième pivot

Veuillez créer un zéro sous le deuxième pivot :

R₃ → R₃ + 7R₂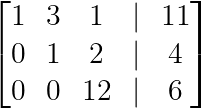

Éliminer en dessous du deuxième pivot. (Image par l'auteur)

La matrice est maintenant sous forme échelonnée par rangs. Nous pouvons l'identifier en vérifiant nos trois critères :

• Aucune ligne ne doit contenir uniquement des zéros (sinon, elles seraient affichées en bas).
• Les pivots forment un escalier : positions (1,1), (2,2) et (3,3)
• Toutes les entrées sous chaque pivot sont égales à zéro.

Résolution de systèmes linéaires à l'aide de la forme échelonnée par lignes

Une fois qu'une matrice est sous forme échelonnée, nous pouvons extraire des solutions à l'aide de la substitution arrière ou analyser les propriétés du système à travers son rang.

Forme échelonnée pour résoudre des équations linéaires

Avec notre matrice sous forme échelonnée, l'approche par substitution arrière peut nous aider à trouver les valeurs des variables en commençant par la ligne du bas et en remontant vers le haut. 

En reprenant notre exemple ci-dessus :

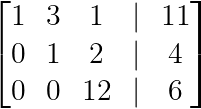
Forme échelonnée (Image par l'auteur)

À partir de la matrice augmentée, nous pouvons écrire le système équivalent :

• x + 3y + z = 11
• y + 2z = 4
• 12z = 6

En commençant par le bas : 

• z = 6/12 = 1/2

En substituant dans la deuxième équation : 

• y + 2(1/2) = 4, donc y = 3

Enfin, en substituant les deux valeurs : 

• x + 3(3) + 1/2 = 11, ce qui donne x = 3/2

Pour les systèmes sous-déterminés (lorsque les variables sont plus nombreuses que les équations), la forme échelonnée par lignes révèle les variables libres.

Prenons un autre exemple similaire :

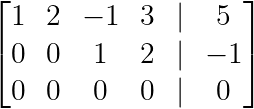
Forme échelonnée des systèmes sous-déterminés. (Image par l'auteur)

Ici, y est une variable libre (pas de pivot dans la colonne 2), ce qui conduit à une solution paramétrique :

• z = -1–2w
• x = 5–2y + z — 3w = 5–2y — 1–5w = 4–2y — 5w

La solution peut être visualisée comme un plan dans un espace à quatre dimensions, paramétré par y et w.

Forme échelonnée des lignes pour déterminer le rang

Le rang d'une matrice est égal au nombre de lignes non nulles dans sa forme échelonnée, ce qui correspond au nombre de pivots. 

Cela nous aide à comprendre l'espace des solutions :

• Si le rang de la matrice de coefficients A est égal au rang de la matrice augmentée [A∣b], et que les deux sont égaux au nombre de variables n, alors le système a une solution unique.
• Si les rangs sont égaux mais inférieurs au nombre de variables, il existe une infinité de solutions en raison des variables libres.
• Si le rang de A est inférieur au rang de [A∣b], le système est incohérent et n'a pas de solution.

Cette approche consistant à utiliser la forme échelonnée par rangées nous permet de comprendre le comportement d'un système avant de le résoudre.

Sujets avancés : Stabilité numérique et pivotement

Si vous souhaitez approfondir vos connaissances sur le REF, cette section explore diverses techniques de pivotement utilisées lors de la transformation de matrices.

Lorsque l'on obtient une forme échelonnée par calcul, le choix du pivot a une incidence significative sur la précision numérique. 

Comprenons cela à l'aide d'un exemple :

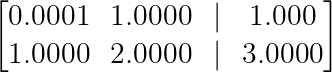
Exemple de stabilité numérique. (Image par l'auteur)

Sans pivotement, nous pouvons diviser la deuxième ligne par 0,0001 pour éliminer le pivot minuscule :

R₂ → R₂ — (1/0.0001)R₁ = R₂ — 10,000R₁

Cette multiplication par 10 000 amplifie les erreurs d'arrondi, ce qui peut compromettre la précision de notre solution. 

Cependant, si nous échangeons d'abord les lignes, la matrice devient :

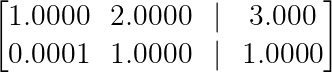
Exemple de stabilité numérique. (Image par l'auteur)

Il ne nous reste plus qu'à utiliser R₂ → R₂ — 0,0001R₁, une opération beaucoup plus stable qui préserve la précision numérique. Cette idée est à la base du pivotement partiel, largement utilisé dans les logiciels numériques.

Pivotement partiel 

Le pivotement partiel sélectionne l'entrée ayant la plus grande valeur absolue dans la colonne actuelle (en commençant par la ligne actuelle vers le bas) et permute les lignes pour placer cette valeur dans la position pivot.

Dans l'exemple ci-dessous, lors du traitement de la colonne 2 :

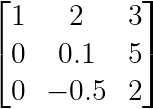
Exemple de pivotement partiel. (Image par l'auteur)

Une rotation partielle permuterait les lignes 2 et 3 pour faire de -0,5 le pivot, car |−0,5| > |0,1|. Cette stratégie améliore la stabilité et est devenue la norme dans les bibliothèques numériques telles que NumPy, SciPy et MATLAB.

Pivotement partiel à l'échelle

Le pivotement partiel à échelle ajoute une étape supplémentaire où chaque entrée candidate est divisée par la plus grande valeur absolue de sa ligne avant de choisir le pivot.

Ce « facteur d'échelle » tient compte de la taille des entrées dans chaque ligne, évitant ainsi tout biais en faveur des lignes contenant naturellement des valeurs élevées.

Pivotement complet

Lors d'un pivotement complet, les lignes et les colonnes sont interverties afin de garantir que le pivot soit la plus grande valeur absolue dans la sous-matrice restante (et pas seulement dans la colonne).

Bien que cela permette d'obtenir le processus d'élimination le plus stable sur le plan numérique, cela entraîne une augmentation de la charge de calcul. Il est donc rarement utilisé dans la pratique, sauf lorsque l'on a besoin d'une précision extrême, comme dans le calcul symbolique ou les simulations scientifiques à enjeux élevés.

Forme échelonnée par rangées Forme échelonnée réduite

Comme nous l'avons vu précédemment, les deux formes sont utiles en algèbre linéaire, mais il est également important de savoir quand utiliser chacune d'elles.

Le tableau ci-dessous résume les différences entre les deux formulaires:

La forme échelonnée par rangs est idéale lorsque nous devons résoudre rapidement un système, en particulier l', pour les matrices de grande taille où les opérations supplémentaires pour la RREF seraient coûteuses. C'est la forme privilégiée pour les algorithmes numériques tels que la décomposition LU.

La forme échelonnée réduite est plus performante à des fins de recherche et théoriques, où il est nécessaire de comprendre directement la structure fondamentale d'une transformation linéaire, de trouver des bases pour les espaces de lignes et de colonnes, ou d'identifier l'indépendance linéaire des vecteurs. Sa représentation unique le rend idéal pour l'analyse théorique et la démonstration automatique de théorèmes.

Conclusion

Dans cet article, nous avons appris comment les opérations élémentaires sur les lignes peuvent transformer des matrices tout en conservant les solutions, et nous avons compris les différences entre REF et RREF. De plus, nous avons découvert des stratégies avancées de pivotement et des variantes de REF qui s'avèrent utiles dans des scénarios particuliers.

Pour approfondir vos connaissances en algèbre linéaire et ses applications en science des données, nous vous invitons à vous inscrire à notre cours Algèbre linéaire pour la science des données, où vous explorerez en détail plusieurs autres concepts et techniques de l'algèbre linéaire, ainsi que les opérations matricielles essentielles.