Explicación de la forma escalonada por filas: Guía para transformar matrices

Si has empezado a estudiar álgebra lineal para la ciencia de datos, probablemente hayas oído hablar a menudo del término «forma escalonada por filas».

La forma escalonada por filas (REF) es una forma de matriz que ayuda a resolver un sistema de ecuaciones lineales. Al transformar una matriz en esta forma especial, podemos determinar si un sistema tiene soluciones, encontrar esas soluciones y comprender la estructura del sistema lineal.

En este artículo, exploraremos qué es la forma escalonada por filas y en qué se diferencia de la forma escalonada reducida por filas. También describiremos el proceso paso a paso para transformar matrices utilizando operaciones elementales con filas, aprenderemos a resolver sistemas lineales mediante sustitución hacia atrás y exploraremos técnicas y conceptos avanzados relacionados con la forma escalonada. 

Conceptos clave detrás de la forma escalonada por filas

Entendamos qué es la forma escalonada por filas y los conceptos clave que la rodean.

¿Qué es la forma escalonada por filas?

Una matriz está en forma escalonada por filas cuando cumple tres condiciones clave:

1. Todas las filas que contienen únicamente ceros se encuentran en la parte inferior de la matriz.
2. La entrada principal (primer elemento distinto de cero) de cada fila distinta de cero aparece a la derecha de la entrada principal de la fila superior.
3. Todas las entradas de una columna debajo de una entrada principal son ceros.

Esto crea un patrón similar a una «escalera» en el que las entradas principales (denominadas pivotes) descienden de izquierda a derecha. 

Por ejemplo, esta matriz está en forma escalonada por filas:

Forma escalonada por filas. (Imagen del autor)

Como vemos arriba, los pivotes (2, 1 y 3) crean el patrón de escalera, con ceros que llenan el espacio debajo de cada pivote. Esta estructura facilita la resolución de sistemas mediante la sustitución hacia atrás (como veremos más adelante).

Forma escalonada reducida (RREF)

La forma escalonada reducida lleva el concepto más allá al añadir dos requisitos adicionales:

1. Cada entrada principal debe tener 1
2. Cada 1 inicial es la única entrada distinta de cero en su columna.

Aquí tienes el mismo sistema anterior, después de transformarlo a RREF:

Forma escalonada reducida. (Imagen del autor)

Aunque un sistema puede tener múltiples formas escalonadas, la forma escalonada reducida es única. 

Esta singularidad hace que la RREF sea útil para identificar la estructura de los conjuntos de soluciones, pero los pasos computacionales adicionales necesarios para lograr la RREF significan que la forma escalonada regular combinada con la sustitución hacia atrás suele ser más eficiente para resolver sistemas.

Operaciones elementales con filas para formar la forma escalonada por filas

Hay tres tipos de operaciones elementales de fila que conservan el conjunto de soluciones al transformar matrices.

Intercambio de filas

Intercambio de filas intercambia dos filas, útil cuando necesitamos colocar un elemento distinto de cero como pivote:

R₁ ↔ R₂

Escalado de filas

Escalado de filas multiplica todos los elementos de una fila por una constante distinta de cero, lo que ayuda a normalizar los valores pivote:

R₁ → cR₁ (where c ≠ 0)

Suma de filas

Adición de filas reemplaza una fila con la suma de sí misma y un múltiplo de otra fila, útil cuando se crean ceros debajo de los pivotes:

R₂ → R₂ + cR₁

Estas operaciones constituyen los pilares de la eliminación gaussiana, el algoritmo que nos permitetransformar sistemáticamente cualquier matriz a forma escalonada por filas, manteniendo el mismo conjunto de soluciones.

Cómo transformar una matriz a forma escalonada por filas

Veamos un ejemplo paso a paso, en el que primero tomamos un sistema lineal y lo reducimos a forma escalonada.

Considera el sistema:

Sistema de ecuaciones lineales. (Imagen del autor)

Paso 1: Escribe la matriz aumentada.

Primero, creamos la matriz aumentada combinando la matriz de coeficientes con las constantes:

Creación de la matriz aumentada (Imagen del autor)

Paso 2: Crear el primer pivote

Queremos que el elemento superior izquierdo sea nuestro primer pivote. Aunque podríamos trabajar con 2, intercambiar filas para obtener 1 como pivote simplifica los cálculos:

R₁ ↔ R₂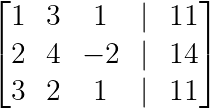

Creación del primer pivote (Imagen del autor)

Paso 3: Elimina por debajo del primer pivote.

Ahora creamos ceros debajo del primer pivote restando los múltiplos adecuados de la fila 1:

R₂ → R₂ - 2R₁
R₃ → R₃ - 3R₁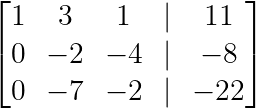

Eliminando por debajo del primer pivote. (Imagen del autor)

Paso 4: Crea el segundo pivote.

Pasando a la segunda columna, podemos simplificar escalando la fila 2:

R₂ → -½R₂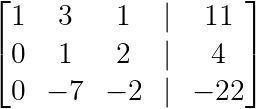

Creación del segundo pivote. (Imagen del autor)

Paso 5: Elimina por debajo del segundo pivote.

Crea un cero debajo del segundo pivote:

R₃ → R₃ + 7R₂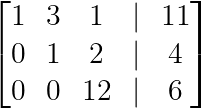

Eliminando por debajo del segundo pivote. (Imagen del autor)

¡La matriz ahora está en forma escalonada por filas! Podemos identificarlo comprobando nuestros tres criterios:

• No hay filas con todos los valores a cero (o estarían al final).
• Los pivotes forman una escalera: posiciones (1,1), (2,2) y (3,3).
• Todas las entradas debajo de cada pivote son cero.

Resolución de sistemas lineales mediante la forma escalonada por filas

Una vez que una matriz está en forma escalonada por filas, podemos extraer soluciones utilizando la sustitución hacia atrás o analizar las propiedades del sistema a través de su rango.

Forma escalonada por filas para resolver ecuaciones lineales

Con nuestra matriz en forma escalonada por filas, el método de sustitución hacia atrás puede ayudarnos a encontrar los valores de las variables empezando por la fila inferior y avanzando hacia arriba. 

Utilizando nuestro ejemplo anterior:

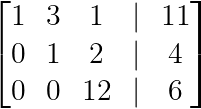
Forma escalonada (Imagen del autor)

A partir de la matriz aumentada, podemos escribir el sistema equivalente:

• x + 3y + z = 11
• y + 2z = 4
• 12z = 6

Empezando desde abajo: 

• z = 6/12 = 1/2

Sustituyendo en la segunda ecuación: 

• y + 2(1/2) = 4, por lo que y = 3

Por último, sustituyendo ambos valores: 

• x + 3(3) + 1/2 = 11, lo que da x = 3/2

Para sistemas subdeterminados (cuando las variables son mayores que las ecuaciones), la forma escalonada por filas revela las variables libres.

Veamos otro ejemplo similar:

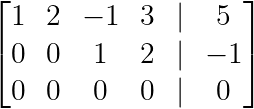
Forma escalonada por filas de sistemas subdeterminados. (Imagen del autor)

Aquí, y es una variable libre (sin pivote en la columna 2), lo que conduce a una solución paramétrica:

• z = -1–2w
• x = 5–2y + z — 3w = 5–2y — 1–5w = 4–2y — 5w

La solución puede entenderse como un plano en un espacio 4D, parametrizado por y y w.

Forma escalonada por filas para hallar el rango

El rango de una matriz es igual al número de filas distintas de cero en su forma escalonada, que corresponde al número de pivotes. 

Esto nos ayuda a comprender el espacio de soluciones:

• Si el rango de la matriz de coeficientes A es igual al rango de la matriz aumentada [A∣b], y ambos son iguales al número de variables n, entonces el sistema tiene una solución única.
• Si los rangos son iguales pero inferiores al número de variables, hay infinitas soluciones debido a las variables libres.
• Si el rango de A es menor que el rango de [A∣b], el sistema es inconsistente y no tiene solución.

Este enfoque de utilizar la forma escalonada por filas nos permite comprender el comportamiento de un sistema antes de resolverlo.

Temas avanzados: Estabilidad numérica y pivote

Si te interesan temas más avanzados relacionados con REF, en esta sección se exploran diversas técnicas de pivote que se utilizan al transformar matrices.

Al llegar a la forma escalonada por filas mediante cálculo, la elección del pivote influye significativamente en la precisión numérica. 

Entendamos esto con un ejemplo:

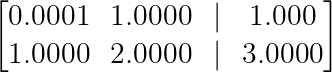
Ejemplo de estabilidad numérica. (Imagen del autor)

Sin pivotar, podemos dividir la segunda fila por 0,0001 para eliminar el pequeño pivote:

R₂ → R₂ — (1/0.0001)R₁ = R₂ — 10,000R₁

Esta multiplicación por 10 000 amplifica cualquier error de redondeo, lo que podría destruir la precisión de nuestra solución. 

Sin embargo, si primero intercambiamos las filas, la matriz queda así:

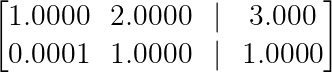
Ejemplo de estabilidad numérica. (Imagen del autor)

Ahora solo necesitamos R₂ → R₂ — 0,0001R₁, una operación mucho más estable que conserva la precisión numérica. Esta idea constituye la base del pivote parcial, que se utiliza ampliamente en el software numérico.

Pivote parcial 

El pivote parcial selecciona la entrada con el valor absoluto más grande en la columna actual (empezando desde la fila actual hacia abajo) e intercambia las filas para colocar ese valor en la posición de pivote.

En el ejemplo siguiente, al procesar la columna 2:

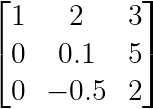
Ejemplo de giro parcial. (Imagen del autor)

El pivote parcial intercambiaría las filas 2 y 3 para hacer -0,5 el pivote, ya que |−0,5| > |0,1|. Esta estrategia mejora la estabilidad y se ha convertido en estándar en bibliotecas numéricas como NumPy, SciPy y MATLAB.

Pivote parcial escalado

El pivote parcial escalado añade un paso adicional en el que cada entrada candidata se divide por el valor absoluto más grande de su fila antes de elegir el pivote.

Este «factor de escala» tiene en cuenta el tamaño de las entradas de cada fila, evitando sesgos hacia las filas con valores naturalmente grandes.

Pivote completo

En el pivote completo, se intercambian tanto las filas como las columnas para garantizar que el pivote sea el valor absoluto más grande de la submatriz restante (no solo de la columna).

Aunque esto da como resultado el proceso de eliminación más estable numéricamente, tiene el inconveniente de aumentar la sobrecarga computacional. Por lo tanto, rara vez se utiliza en la práctica, a menos que se requiera una precisión extrema, como en el cálculo simbólico o en simulaciones científicas de alto riesgo.

Forma escalonada por filas frente a Forma escalonada reducida

Como hemos aprendido anteriormente, ambas formas son útiles en álgebra lineal, pero también es necesario saber cuándo utilizar cada una de ellas.

La tabla siguiente resume las diferencias entre los dos formularios:

La forma escalonada por filas es la mejor opción cuando necesitamos resolver un sistema rápidamente, especialmente e o de matrices grandes, donde las operaciones adicionales para RREF serían costosas. Es la forma preferida para algoritmos numéricos como la descomposición LU.

La forma escalonada reducida ofrece mejores resultados para fines teóricos y de investigación, en los que necesitamos comprender directamente la estructura fundamental de una transformación lineal, encontrar bases para los espacios de filas y columnas o identificar la independencia lineal de vectores. Su representación única lo hace ideal para el análisis teórico y la demostración automática de teoremas.

Conclusión

En este artículo, hemos aprendido cómo las operaciones elementales con filas pueden transformar matrices conservando las soluciones, y hemos comprendido las diferencias entre REF y RREF. Además, aprendimos algunas estrategias avanzadas de pivote y variaciones de REF que resultan útiles en situaciones especiales.

Para profundizar en tus conocimientos sobre álgebra lineal y sus aplicaciones en la ciencia de datos, te recomendamos que te inscribas en nuestro curso Álgebra lineal para la ciencia de datos, donde profundizarás en otros conceptos y técnicas de álgebra lineal, además de aprender operaciones matriciales esenciales.