Erklärung der Zeilen-Ebenenform: Ein Leitfaden zur Transformation von Matrizen

Wenn du gerade mit dem Lernen von linearer Algebra für die Datenwissenschaft angefangen hast, hast du wahrscheinlich schon oft den Begriff „Zeilenstufenform“ gehört.

Die Zeilenstufenform (REF) ist eine Form einer Matrix, die beim Lösen eines linearen Gleichungssystems hilft. Indem wir eine Matrix in diese spezielle Form umwandeln, können wir herausfinden, ob ein System Lösungen hat, diese Lösungen finden und die Struktur des linearen Systems verstehen.

In diesem Artikel schauen wir uns an, was die Zeilenstufenform ist und wie sie sich von der reduzierten Zeilenstufenform unterscheidet. Außerdem zeigen wir dir Schritt für Schritt, wie du Matrizen mit einfachen Zeilenoperationen umwandelst, wie du lineare Gleichungssysteme mit Rückwärtssubstitution löst und gehen auf fortgeschrittene Techniken und Konzepte im Zusammenhang mit der Zeilenstufentheorie ein. 

Wichtige Konzepte hinter der Zeilenstufenform

Schauen wir mal, was eine Zeilenstufenform ist und was die wichtigsten Sachen dazu sind.

Was ist eine Zeilenstufenform?

Eine Matrix ist in Zeilenstufenform, wenn sie drei wichtige Bedingungen erfüllt:

1. Alle Zeilen, die nur aus Nullen bestehen, sind unten in der Matrix.
2. Der erste Eintrag (das erste Element, das nicht Null ist) jeder Zeile, die nicht Null ist, kommt rechts neben dem ersten Eintrag in der Zeile darüber.
3. Alle Einträge in einer Spalte unter einem ersten Eintrag sind Nullen.

Dadurch entsteht ein „treppenartiges“ Muster, bei dem die führenden Einträge (sogenannte Pivots) von links nach rechts abfallen. 

Diese Matrix ist zum Beispiel in Zeilenstufenform:

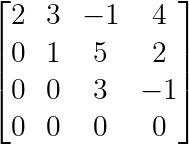
Zeilen-Ebenenform. (Bild vom Autor)

Wie wir oben sehen können, bilden die Drehpunkte (2, 1 und 3) das Treppenmuster, wobei die Nullen den Raum unter jedem Drehpunkt ausfüllen. Diese Struktur macht es einfach, Systeme durch Rückwärtssubstitution zu lösen (wie wir später sehen werden).

Reduzierte Zeilenstufenform (RREF)

Die reduzierte Zeilenstufenform geht noch einen Schritt weiter und hat zwei zusätzliche Regeln:

1. Jeder erste Eintrag muss 1 sein.
2. Jede führende 1 ist der einzige Eintrag ungleich Null in ihrer Spalte.

Hier ist das gleiche System wie oben, nachdem es in RREF umgewandelt wurde:

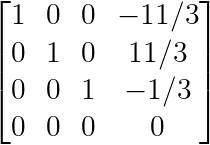
Reduzierte Zeilen-Ebenenform. (Bild vom Autor)

Obwohl ein System mehrere Zeilenstufenformen haben kann, ist die reduzierte Zeilenstufenform einzigartig. 

Diese Besonderheit macht die RREF super, um die Struktur von Lösungsmengen zu erkennen. Aber wegen der zusätzlichen Schritte, die man für die RREF braucht, ist die normale Zeilenstufenform zusammen mit der Rückwärtssubstitution oft besser, um Systeme zu lösen.

Einfache Zeilenoperationen zur Bildung der Zeilenstufenform

Es gibt drei Arten von elementaren Zeilenoperationen, die die Lösungsmenge bei der Transformation von Matrizen beibehalten.

Zeilen tauschen

Zeilen tauschen tauscht zwei Zeilen, was praktisch ist, wenn wir ein Element ungleich Null als Drehpunkt setzen wollen:

R₁ ↔ R₂

Zeilen skalieren

Zeilen skalieren multipliziert alle Elemente in einer Zeile mit einer Konstante ungleich Null, um die Pivot-Werte zu normalisieren:

R₁ → cR₁ (where c ≠ 0)

Zeilenaddition

Zeilenaddition ersetzt eine Zeile durch die Summe aus sich selbst und einem Vielfachen einer anderen Zeile. Das ist nützlich, wenn man unterhalb von Pivots Nullen erstellen will:

R₂ → R₂ + cR₁

Diese Operationen sind die Bausteine der Gaußschen Eliminationsverfahren, dem Algorithmus, mit dem wirjede Matrix systematisch in Zeilenstufenform umwandeln können, ohne die Lösungsmenge zu verändern.

Wie man eine Matrix in eine Zeilenstufenform umwandelt

Schauen wir uns das mal Schritt für Schritt an einem Beispiel an, wo wir erst ein lineares System nehmen und es in Zeilenstufenform bringen.

Schau dir mal das System an:

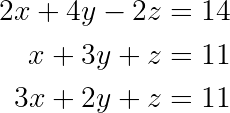
Lineares Gleichungssystem. (Bild vom Autor)

Schritt 1: Schreib die erweiterte Matrix auf.

Zuerst machen wir die erweiterte Matrix, indem wir die Koeffizientenmatrix mit den Konstanten zusammenwerfen:

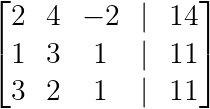
Erstellen der erweiterten Matrix (Bild vom Autor)

Schritt 2: Erstelle den ersten Pivot

Wir wollen, dass das Element oben links unser erster Drehpunkt ist. Wir könnten zwar mit 2 arbeiten, aber das Vertauschen der Zeilen, um 1 als Drehpunkt zu erhalten, vereinfacht die Berechnungen:

R₁ ↔ R₂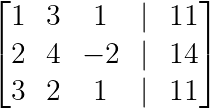

Erstellen des ersten Drehpunkts (Bild vom Autor)

Schritt 3: Unterhalb des ersten Drehpunkts löschen

Jetzt machen wir unter dem ersten Drehpunkt Nullen, indem wir die entsprechenden Vielfachen von Zeile 1 abziehen:

R₂ → R₂ - 2R₁
R₃ → R₃ - 3R₁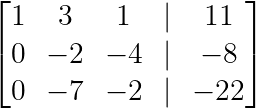

Unterhalb des ersten Drehpunkts eliminieren. (Bild vom Autor)

Schritt 4: Erstell den zweiten Drehpunkt

In der zweiten Spalte können wir das Ganze vereinfachen, indem wir Zeile 2 skalieren:

R₂ → -½R₂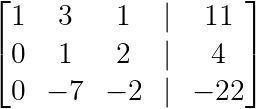

Erstellen des zweiten Drehpunkts. (Bild vom Autor)

Schritt 5: Entferne alles unterhalb des zweiten Drehpunkts.

Mach eine Null unter dem zweiten Drehpunkt:

R₃ → R₃ + 7R₂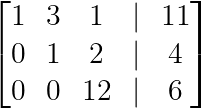

Unterhalb des zweiten Drehpunkts eliminieren. (Bild vom Autor)

Die Matrix ist jetzt in Zeilenstufenform! Wir können das anhand unserer drei Kriterien feststellen:

• Keine Zeilen, die nur aus Nullen bestehen (sonst wären sie ganz unten)
• Die Drehpunkte bilden eine Treppe: Positionen (1,1), (2,2) und (3,3)
• Alle Einträge unter jedem Drehpunkt sind Null.

Lineare Gleichungssysteme mit Hilfe der Zeilenstufenform lösen

Sobald eine Matrix in Zeilenstufenform ist, können wir Lösungen durch Zurücksetzen finden oder die Eigenschaften des Systems anhand seines Ranges analysieren.

Zeilenstufenform zum Lösen linearer Gleichungen

Mit unserer Matrix in Zeilenstufenform können wir mit der Rückaustauschmethode die Werte der Variablen von der untersten Zeile aus nach oben suchen. 

Nimm unser Beispiel von oben:

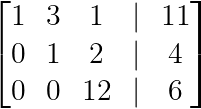
Zeilen-Ebenen-Form (Bild vom Autor)

Aus der erweiterten Matrix können wir das entsprechende System schreiben:

• x + 3y + z = 11
• y + 2z = 4
• 12z = 6

Von ganz unten anfangen: 

• z = 6/12 = 1/2

Das in die zweite Gleichung einsetzen: 

• y + 2(1/2) = 4, so y = 3

Zum Schluss setzt man beide Werte ein: 

• x + 3(3) + 1/2 = 11, also x = 3/2

Bei unterbestimmten Systemen (wenn es mehr Variablen als Gleichungen gibt) zeigt die Zeilenstufenform freie Variablen.

Schauen wir uns noch ein Beispiel an:

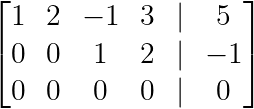
Zeilenstufenform unterbestimmter Systeme. (Bild vom Autor)

Hier ist y eine freie Variable (kein Pivot in Spalte 2), was zu einer parametrischen Lösung führt:

• z = -1–2w
• x = 5–2y + z — 3w = 5–2y — 1–5w = 4–2y — 5w

Die Lösung kann man sich so vorstellen, dass sie eine Ebene im 4D-Raum bildet, die durch y und w parametrisiert ist.

Zeilenstufenform zum Bestimmen des Ranges

Der Rang einer Matrix ist gleich der Anzahl der Zeilen, die in ihrer Zeilenstufenform nicht null sind, was der Anzahl der Pivotstellen entspricht. 

Das hilft uns, den Lösungsraum zu verstehen:

• Wenn der Rang der Koeffizientenmatrix A dem Rang der erweiterten Matrix [A∣b] entspricht und beide der Anzahl der Variablen n entsprechen, dann hat das System eine eindeutige Lösung.
• Wenn die Ränge gleich sind, aber weniger als die Anzahl der Variablen, gibt es wegen der freien Variablen unendlich viele Lösungen.
• Wenn der Rang von A kleiner ist als der Rang von [A∣b], ist das System inkonsistent und hat keine Lösung.

Mit diesem Ansatz der Zeilenstufenform können wir das Verhalten eines Systems verstehen, bevor wir es lösen.

Fortgeschrittene Themen: Numerische Stabilität und Pivoting

Wenn du dich für fortgeschrittenere Themen im Zusammenhang mit REF interessierst, findest du in diesem Abschnitt verschiedene Pivotierungstechniken, die bei der Transformation von Matrizen verwendet werden.

Wenn man bei der Berechnung zur Zeilenstufenform kommt, ist die Wahl des Pivot-Elements echt wichtig für die numerische Genauigkeit. 

Schauen wir uns das mal mit einem Beispiel an:

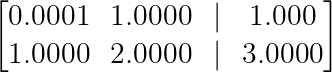
Beispiel für numerische Stabilität. (Bild vom Autor)

Ohne Pivotierung können wir die zweite Zeile durch 0,0001 teilen, um den winzigen Pivot zu entfernen:

R₂ → R₂ — (1/0.0001)R₁ = R₂ — 10,000R₁

Diese Multiplikation mit 10.000 verstärkt alle Rundungsfehler und kann die Genauigkeit unserer Lösung beeinträchtigen. 

Wenn wir aber erst die Zeilen tauschen, sieht die Matrix so aus:

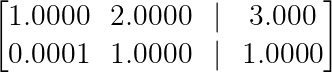
Beispiel für numerische Stabilität. (Bild vom Autor)

Jetzt brauchen wir nur noch R₂ → R₂ — 0,0001R₁, was viel stabiler ist und die numerische Genauigkeit beibehält. Diese Idee ist die Basis für das partielle Pivoting, das in numerischer Software oft verwendet wird.

Teilweise Schwenken 

Teilweise Drehung wählt den Eintrag mit dem größten absoluten Wert in der aktuellen Spalte (von der aktuellen Zeile abwärts) und tauscht Zeilen, um diesen Wert in die Drehposition zu bringen.

Im folgenden Beispiel wird bei der Verarbeitung von Spalte 2:

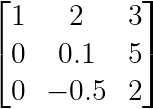
Beispiel für eine teilweise Drehung. (Bild vom Autor)

Durch teilweises Drehen werden die Zeilen 2 und 3 getauscht, sodass -0,5 zum Drehpunkt wird, da |−0,5| > |0,1| ist. Diese Strategie macht das Ganze stabiler und ist mittlerweile Standard in numerischen Bibliotheken wie NumPy, SciPy und MATLAB.

Skaliertes teilweises Drehen

Skaliertes partielles Pivoting macht einen zusätzlichen Schritt, bei dem jeder mögliche Eintrag durch den größten absoluten Wert in seiner Zeile geteilt wird, bevor der Pivot ausgewählt wird.

Dieser „Skalierungsfaktor“ berücksichtigt die Größe der Einträge in jeder Zeile und verhindert so, dass Zeilen mit von Natur aus großen Werten bevorzugt werden.

Komplett drehbar

Bei einer kompletten Drehung werden sowohl die Zeilen als auch die Spalten getauscht, damit der Drehpunkt den größten absoluten Wert in der verbleibenden Untermatrix hat (nicht nur in der Spalte).

Das führt zwar zu einem zahlenmäßig stabileren Eliminierungsprozess, aber es kostet mehr Rechenzeit. Deshalb wird es in der Praxis kaum benutzt, außer wenn es auf extreme Genauigkeit ankommt, wie bei symbolischen Berechnungen oder wichtigen wissenschaftlichen Simulationen.

Zeilen-Ebenenform vs. Reduzierte Zeilenstufenform

Wie wir schon gesehen haben, sind beide Formen in der linearen Algebra nützlich, aber wir müssen auch wissen, wann wir welche Form verwenden müssen.

Die Tabelle unten zeigt die Unterschiede zwischen den beiden Formen:

Die Zeilenstufenform ist super, wenn wir ein System schnell lösen müssen, vor allem bei der Reduktion in die Normalform ( ) für große Matrizen, wo die zusätzlichen Schritte für die RREF ziemlich aufwendig wären. Das ist die beste Form für numerische Algorithmen wie die LU-Zerlegung.

Die reduzierte Zeilenstufenform ist besser für Forschung und Theorie, wo wir die grundlegende Struktur einer linearen Transformation direkt verstehen, Basen für Zeilen- und Spaltenräume finden oder die lineare Unabhängigkeit von Vektoren erkennen müssen. Die einzigartige Darstellung macht es super für theoretische Analysen und automatisierte Theorembeweise.

Fazit

In diesem Artikel haben wir gelernt, wie man mit einfachen Zeilenoperationen Matrizen verändern kann, ohne die Lösungen zu verändern, und haben die Unterschiede zwischen REF und RREF verstanden. Außerdem haben wir ein paar fortgeschrittene Pivotierungsstrategien und Varianten von REF gelernt, die in bestimmten Situationen echt nützlich sind.

Wenn du dein Wissen über lineare Algebra und ihre Anwendungen in der Datenwissenschaft vertiefen willst, solltest du unseren Kurs „Lineare Algebra für Datenwissenschaft“ checken. Dort lernst du neben den grundlegenden Matrixoperationen auch viele andere Konzepte und Techniken der linearen Algebra kennen.