Explicação da forma escalonada em linha: Um guia para transformar matrizes

Se você começou a aprender álgebra linear para ciência de dados, provavelmente já ouviu falar bastante sobre “forma escalonada por linhas”.

A forma escalonada por linhas (REF) é uma forma de matriz que ajuda a resolver um sistema de equações lineares. Ao transformar uma matriz nessa forma especial, a gente consegue saber se um sistema tem soluções, encontrar essas soluções e entender a estrutura do sistema linear.

Neste artigo, vamos ver o que é a forma escalonada por linhas e como ela é diferente da forma escalonada reduzida por linhas. Também vamos mostrar passo a passo como transformar matrizes usando operações elementares de linhas, aprender a resolver sistemas lineares usando substituição por trás e explorar técnicas e conceitos avançados relacionados à forma escalonada por linhas. 

Conceitos-chave por trás da forma escalonada por linhas

Vamos entender o que é a forma escalonada por linhas e os conceitos principais relacionados a ela.

O que é a forma escalonada por linhas?

Uma matriz está na forma escalonada em linhas quando cumpre três condições principais:

1. Todas as linhas que só têm zeros estão na parte de baixo da matriz.
2. A entrada principal (primeiro elemento diferente de zero) de cada linha diferente de zero aparece à direita da entrada principal na linha acima dela.
3. Todas as entradas numa coluna abaixo de uma entrada inicial são zeros.

Isso cria um padrão tipo “escada”, onde as entradas principais (chamadas pivôs) descem da esquerda para a direita. 

Por exemplo, essa matriz está na forma escalonada por linhas:

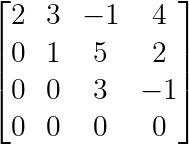
Forma escalonada em linha. (Imagem do autor)

Como a gente vê aí em cima, os pivôs (2, 1 e 3) fazem o padrão de escada, com zeros enchendo o espaço embaixo de cada pivô. Essa estrutura facilita resolver sistemas por meio da substituição por trás (como vamos ver mais tarde).

Forma reduzida em escalão (RREF)

A forma escalonada reduzida leva o conceito mais longe, adicionando dois requisitos extras:

1. Cada entrada principal deve ter 1
2. Cada 1 na frente é o único valor diferente de zero na coluna dele.

Aqui tá o mesmo sistema de cima, depois de transformar pra RREF:

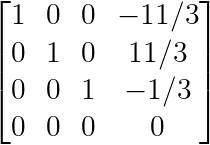
Forma reduzida em escalões. (Imagem do autor)

Embora um sistema possa ter várias formas escalonadas, a forma escalonada reduzida é única. 

Essa singularidade torna a RREF útil para identificar a estrutura dos conjuntos de soluções, mas as etapas computacionais adicionais necessárias para alcançar a RREF significam que a forma escalonada regular combinada com a substituição por trás é frequentemente mais eficiente para resolver sistemas.

Operações elementares com linhas para formar a forma escalonada por linhas

Existem três tipos de operações elementares de linha que mantêm o conjunto de soluções enquanto transformam matrizes.

Troca de linhas

Troca de linhas troca duas linhas, útil quando precisamos colocar um elemento diferente de zero como pivô:

R₁ ↔ R₂

Escalonamento de linhas

Escalonamento de linha multiplica todos os elementos em uma linha por uma constante diferente de zero, ajudando a normalizar os valores pivô:

R₁ → cR₁ (where c ≠ 0)

Adição de linhas

Adição de linhas substitui uma linha pela soma dela mesma e um múltiplo de outra linha, útil quando se cria zeros abaixo dos pivôs:

R₂ → R₂ + cR₁

Essas operações são a base da eliminação gaussiana, o algoritmo que nos permitetransformar sistematicamente qualquer matriz em forma escalonada por linhas, mantendo o mesmo conjunto de soluções.

Como transformar uma matriz em forma escalonada por linhas

Vamos ver um exemplo passo a passo, onde primeiro pegamos um sistema linear e o reduzimos à forma escalonada.

Pensa no sistema:

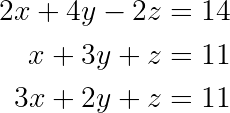
Sistema de equações lineares. (Imagem do autor)

Passo 1: Escreva a matriz aumentada

Primeiro, criamos a matriz aumentada juntando a matriz de coeficientes com as constantes:

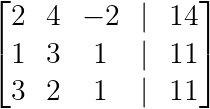
Criando a matriz aumentada (Imagem do autor)

Passo 2: Crie o primeiro pivô

Queremos que o elemento no canto superior esquerdo seja o nosso primeiro pivô. Embora pudéssemos trabalhar com 2, trocar as linhas para obter 1 como pivô simplifica os cálculos:

R₁ ↔ R₂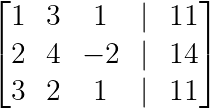

Criando o primeiro pivô (Imagem do autor)

Passo 3: Tira tudo que tá abaixo do primeiro ponto de referência.

Agora criamos zeros abaixo do primeiro pivô subtraindo os múltiplos apropriados da linha 1:

R₂ → R₂ - 2R₁
R₃ → R₃ - 3R₁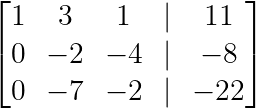

Eliminando abaixo do primeiro pivô. (Imagem do autor)

Passo 4: Crie o segundo pivô

Passando para a segunda coluna, dá pra simplificar redimensionando a linha 2:

R₂ → -½R₂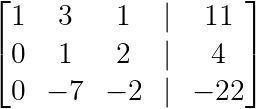

Criando o segundo pivô. (Imagem do autor)

Passo 5: Tira tudo que tá abaixo do segundo ponto de rotação.

Crie um zero abaixo do segundo pivô:

R₃ → R₃ + 7R₂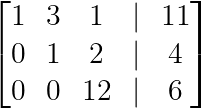

Eliminando abaixo do segundo pivô. (Imagem do autor)

A matriz agora está na forma escalonada! A gente consegue identificar isso verificando nossos três critérios:

• Sem linhas só com zeros (ou elas ficariam na parte de baixo)
• Os pivôs formam uma escada: posições (1,1), (2,2) e (3,3)
• Todas as entradas abaixo de cada pivô são zero.

Resolvendo sistemas lineares usando a forma escalonada por linhas

Quando uma matriz está na forma escalonada, dá pra extrair soluções usando substituição por trás ou analisar as propriedades do sistema através do seu grau.

Forma escalonada por linhas para resolver equações lineares

Com a nossa matriz em forma escalonada, a abordagem de substituição para trás pode ajudar a encontrar valores variáveis começando pela linha inferior e indo para cima. 

Usando o nosso exemplo acima:

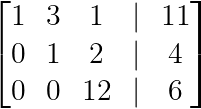
Forma escalonada (Imagem do autor)

A partir da matriz aumentada, podemos escrever o sistema equivalente:

• x + 3y + z = 11
• y + 2z = 4
• 12z = 6

Começando do zero: 

• z = 6/12 = 1/2

Substituindo na segunda equação: 

• y + 2(1/2) = 4, então y = 3

Por fim, substituindo os dois valores: 

• x + 3(3) + 1/2 = 11, o que dá x = 3/2

Para sistemas subdeterminados (quando as variáveis são maiores que as equações), a forma escalonada por linhas mostra as variáveis livres.

Vamos ver outro exemplo:

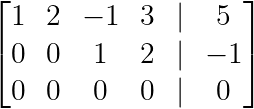
Forma escalonada de sistemas subdeterminados. (Imagem do autor)

Aqui, y é uma variável livre (sem pivô na coluna 2), levando a uma solução paramétrica:

• z = -1–2w
• x = 5–2y + z — 3w = 5–2y — 1–5w = 4–2y — 5w

A solução pode ser entendida como um plano no espaço 4D, com os parâmetros y e w.

Forma escalonada por linhas para encontrar a classificação

A classificação de uma matriz é igual ao número de linhas diferentes de zero na sua forma escalonada, que é o mesmo que o número de pivôs. 

Isso nos ajuda a entender o espaço de soluções:

• Se o grau da matriz de coeficientes A for igual ao grau da matriz aumentada [A∣b] e ambos forem iguais ao número de variáveis n, então o sistema tem uma solução única.
• Se as classificações forem iguais, mas menores que o número de variáveis, tem um monte de soluções por causa das variáveis livres.
• Se a classificação de A for menor que a classificação de [A∣b], o sistema é inconsistente e não tem solução.

Essa abordagem de usar a forma escalonada por linhas nos ajuda a entender como um sistema funciona antes de resolver o problema.

Tópicos avançados: Estabilidade numérica e pivô

Se você quiser saber mais sobre REF, essa seção fala sobre várias técnicas de pivô usadas pra transformar matrizes.

Quando chegamos à forma escalonada computacionalmente, a escolha do pivô tem um impacto significativo na precisão numérica. 

Vamos entender isso com um exemplo:

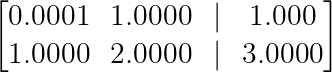
Exemplo de estabilidade numérica. (Imagem do autor)

Sem pivotar, podemos dividir a segunda linha por 0,0001 para eliminar o pequeno pivô:

R₂ → R₂ — (1/0.0001)R₁ = R₂ — 10,000R₁

Essa multiplicação por 10.000 aumenta qualquer erro de arredondamento, podendo acabar com a precisão da nossa solução. 

Mas, se trocarmos as linhas primeiro, a matriz fica assim:

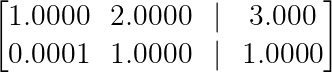
Exemplo de estabilidade numérica. (Imagem do autor)

Agora só precisamos de R₂ → R₂ — 0,0001R₁, uma operação muito mais estável que mantém a precisão numérica. Essa ideia é a base do pivô parcial, que é muito usado em programas de computador.

Giro parcial 

A rotação parcial escolhe a entrada com o maior valor absoluto na coluna atual (começando da linha atual para baixo) e troca as linhas para colocar esse valor na posição de rotação.

No exemplo abaixo, ao processar a coluna 2:

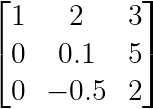
Exemplo de rotação parcial. (Imagem do autor)

A rotação parcial trocaria as linhas 2 e 3 para fazer -0,5 o pivô, já que |−0,5| é maior que |0,1|. Essa estratégia melhora a estabilidade e já virou padrão em bibliotecas numéricas como NumPy, SciPy e MATLAB.

Pivô parcial em escala

A rotação parcial escalonada adiciona uma etapa extra em que cada entrada candidata é dividida pelo maior valor absoluto em sua linha antes de escolher o pivô.

Esse “fator de escala” leva em conta o tamanho das entradas em cada linha, evitando que as linhas com valores naturalmente grandes sejam mais favorecidas.

Pivô completo

Na rotação completa, as linhas e colunas são trocadas para garantir que o pivô seja o maior valor absoluto na submatriz restante (não só na coluna).

Embora isso resulte no processo de eliminação mais estável em termos numéricos, isso tem o custo de um aumento da sobrecarga computacional. Por isso, raramente é usado na prática, a menos que seja necessária uma precisão extrema, como em cálculos simbólicos ou simulações científicas de alto risco.

Forma escalonada em linha vs. Forma escalonada reduzida

Como vimos antes, as duas formas são úteis na álgebra linear, mas também precisamos saber quando usar cada uma delas.

A tabela abaixo mostra as diferenças entre os dois formulários:

A forma escalonada por linhas é melhor quando precisamos resolver um sistema rapidinho, principalmente pra matrizes grandes ( ), onde as operações extras pra RREF seriam caras. É a forma preferida para algoritmos numéricos como a decomposição LU.

A forma escalonada reduzida funciona melhor para fins de pesquisa e teóricos, onde precisamos entender direto a estrutura básica de uma transformação linear, encontrar bases para espaços de linhas e colunas ou identificar a independência linear de vetores. A representação única torna-o ideal para análises teóricas e provas automáticas de teoremas.

Conclusão

Neste artigo, a gente aprendeu como as operações elementares com linhas podem transformar matrizes sem mudar as soluções e entendemos as diferenças entre REF e RREF. Além disso, aprendemos algumas estratégias avançadas de pivô e variações do REF que são úteis em cenários especiais.

Para entender melhor a álgebra linear e como ela pode ajudar na ciência de dados, dá uma olhada no nosso curso Álgebra Linear para Ciência de Dados, onde você vai aprender mais sobre vários outros conceitos e técnicas da álgebra linear, além das operações essenciais com matrizes.