Row Echelon Form Explained: A Guide to Transforming Matrices

If you’ve been starting to learn linear algebra for data science, you probably heard the term "row echelon form" coming up quite often.

Row echelon form (REF) is a form of a matrix that helps in solving a system of linear equations. By transforming a matrix into this special form, we can determine whether a system has solutions, find those solutions, and understand the structure of the linear system.

In this article, we’ll explore what row echelon form is and how it differs from reduced row echelon form. We’ll also outline the step-by-step process of transforming matrices using elementary row operations, learn how to solve linear systems using back-substitution, and explore advanced techniques and concepts related to row echelon form. 

Key Concepts Behind Row Echelon Form

Let’s understand what row echelon form is and the key concepts around it.

What is row echelon form?

A matrix is in row echelon form when it satisfies three key conditions:

1. All rows consisting entirely of zeros are at the bottom of the matrix
2. The leading entry (first nonzero element) of each nonzero row appears to the right of the leading entry in the row above it
3. All entries in a column below a leading entry are zeros

This creates a “staircase” like pattern where the leading entries (called pivots) descend from left to right. 

For example, this matrix is in row echelon form:

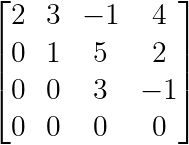
Row echelon form. (Image by Author)

As we see above, the pivots (2, 1, and 3) create the staircase pattern, with zeros filling the space below each pivot. This structure makes it straightforward to solve systems through back-substitution (as we’ll explore later).

Reduced row echelon form (RREF)

Reduced row echelon form takes the concept further by adding two additional requirements:

1. Every leading entry must be 1
2. Each leading 1 is the only nonzero entry in its column

Here’s the same system above, after transforming to RREF:

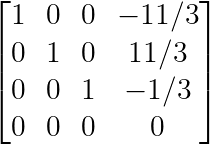
Reduced row-echelon form. (Image by Author)

Though a system can have multiple row echelon forms, the reduced row echelon form is unique. 

This uniqueness makes RREF useful for identifying the structure of solution sets, but the additional computational steps required to achieve RREF mean that regular row echelon form combined with back-substitution is often more efficient for solving systems.

Elementary row operations to form the row echelon form

There are three types of elementary row operations that preserve the solution set while transforming matrices.

Row swapping

Row swapping exchanges two rows, useful when we need to position a nonzero element as a pivot:

R₁ ↔ R₂

Row scaling

Row scaling multiplies all elements in a row by a nonzero constant, helping normalize pivot values:

R₁ → cR₁ (where c ≠ 0)

Row addition

Row addition replaces one row with the sum of itself and a multiple of another row, helpful when creating zeros below pivots:

R₂ → R₂ + cR₁

These operations form the building blocks of Gaussian elimination, the algorithm that allows us to systematically transform any matrix into row echelon form while maintaining the same solution set.

How to Transform a Matrix to Row Echelon Form

Let’s work through an example in a step-by-step manner, where we first take a linear system and reduce it to row echelon form.

Consider the system:

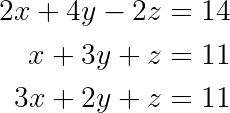
System of linear equations. (Image by Author)

Step 1: Write the augmented matrix

First, we create the augmented matrix by combining the coefficient matrix with the constants:

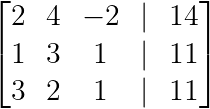
Creating the augmented matrix (Image by Author)

Step 2: Create the first pivot

We want the top-left element to be our first pivot. While we could work with 2, swapping rows to get 1 as the pivot simplifies calculations:

R₁ ↔ R₂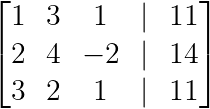

Creating the first pivot (Image by Author)

Step 3: Eliminate below the first pivot

Now we create zeros below the first pivot by subtracting appropriate multiples of row 1:

R₂ → R₂ - 2R₁
R₃ → R₃ - 3R₁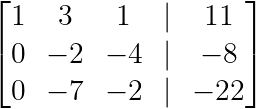

Eliminating below the first pivot. (Image by Author)

Step 4: Create the second pivot

Moving to the second column, we can simplify by scaling row 2:

R₂ → -½R₂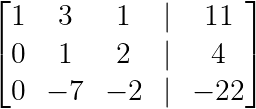

Creating the second pivot. (Image by Author)

Step 5: Eliminate below the second pivot

Create a zero below the second pivot:

R₃ → R₃ + 7R₂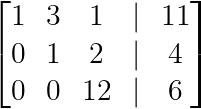

Eliminating below the second pivot. (Image by Author)

The matrix is now in row echelon form! We can identify this by checking our three criteria:

• No all-zero rows (or they would be at the bottom)
• Pivots form a staircase: positions (1,1), (2,2), and (3,3)
• All entries below each pivot are zero

Solving Linear Systems Using Row Echelon Form

Once a matrix is in row echelon form, we can extract solutions using back-substitution or analyze the system’s properties through its rank.

Row echelon form for solving linear equations

With our matrix in row echelon form, the back-substitution approach can help us find variable values starting from the bottom row and working upward. 

Using our example above:

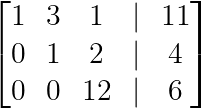
Row-echelon form (Image by Author)

From the augmented matrix, we can write the equivalent system:

• x + 3y + z = 11
• y + 2z = 4
• 12z = 6

Starting from the bottom: 

• z = 6/12 = 1/2

Substituting into the second equation: 

• y + 2(1/2) = 4, so y = 3

Finally, substituting both values: 

• x + 3(3) + 1/2 = 11, giving x = 3/2

For underdetermined systems (when the variables are greater than the equations), the row echelon form reveals free variables.

Let us see another such example:

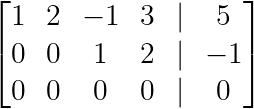
Row echelon form of underdetermined systems. (Image by Author)

Here, y is a free variable (no pivot in column 2), leading to a parametric solution:

• z = -1–2w
• x = 5–2y + z — 3w = 5–2y — 1–5w = 4–2y — 5w

The solution can be understood as it forms a plane in 4D space, parameterized by y and w.

Row echelon form for finding the rank

The rank of a matrix is equal to the number of non-zero rows in its row echelon form, which corresponds to the number of pivots. 

This helps us understand the solution space:

• If the rank of the coefficient matrix A equals the rank of the augmented matrix [A∣b], and both equal the number of variables n, then the system has a unique solution.
• If the ranks are equal but less than the number of variables, there are infinitely many solutions due to free variables.
• If the rank of A is less than the rank of [A∣b], the system is inconsistent and has no solution.

This approach of using row echelon form allows us to understand the behavior of a system before solving it.

Advanced Topics: Numerical Stability and Pivoting

If you’re interested in more advanced topics related to REF, this section explores various pivoting techniques used when transforming matrices.

When arriving at row echelon form computationally, the choice of pivot significantly impacts numerical accuracy. 

Let’s understand this with an example:

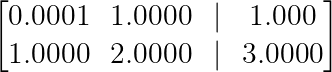
Numerical stability example. (Image by Author)

Without pivoting, we can divide the second row by 0.0001 to eliminate the tiny pivot:

R₂ → R₂ — (1/0.0001)R₁ = R₂ — 10,000R₁

This multiplication by 10,000 amplifies any rounding errors, potentially destroying the accuracy of our solution. 

However, if we swap the rows first, the matrix becomes:

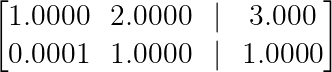
Numerical stability example. (Image by Author)

Now we only need R₂ → R₂ — 0.0001R₁, a much more stable operation that preserves numerical accuracy. This idea forms the basis of partial pivoting, which is widely used in numerical software.

Partial pivoting 

Partial pivoting selects the entry with the largest absolute value in the current column (starting from the current row downwards) and swaps rows to bring that value into the pivot position.

In the example below, when processing column 2:

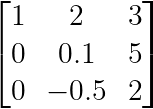
Partial pivoting example. (Image by Author)

Partial pivoting would swap rows 2 and 3 to make -0.5 the pivot, as |−0.5| > |0.1|. This strategy improves stability and has become standard in numerical libraries like NumPy, SciPy, and MATLAB.

Scaled partial pivoting

Scaled partial pivoting adds an extra step where each candidate entry is divided by the largest absolute value in its row before choosing the pivot.

This “scaling factor” accounts for the size of entries in each row, avoiding bias toward rows with naturally large values.

Complete pivoting

In complete pivoting, both rows and columns are interchanged to ensure that the pivot is the largest absolute value in the remaining submatrix (not just the column).

Although this results in the most numerically stable elimination process, it comes at the cost of increased computational overhead. So it’s rarely used in practice unless extreme precision is needed, such as in symbolic computation or high-stakes scientific simulations.

Row Echelon Form vs. Reduced Row Echelon Form

As we learned earlier, both forms are useful in linear algebra, but we also need to know when to use each of the forms.

The table below summarizes the differences between the two forms:

Row echelon form is best when we need to solve a system quickly, especially for large matrices where the additional operations for RREF would be costly. It’s the preferred form for numerical algorithms like LU decomposition.

Reduced row echelon form performs better for research and theoretical purposes, where we need to directly understand the fundamental structure of a linear transformation, find bases for row and column spaces, or identify linear independence of vectors. The unique representation makes it ideal for theoretical analysis and automated theorem proving.

Conclusion

In this article, we learned how elementary row operations can transform matrices while preserving solutions, and understood the differences between REF and RREF. Further, we learned some advanced pivoting strategies and variations of REF that become useful in special scenarios.

To deepen your understanding of linear algebra and its applications in data science, consider enrolling in our Linear Algebra for Data Science course, where you’ll dive deeper into several other concepts and techniques in linear algebra alongside essential matrix operations.