Modélisation des équations structurelles : Qu'est-ce que c'est et quand l'utiliser ?

La modélisation par équations structurelles (SEM) nous permet d'étudier les relations causales entre les variables et de comprendre comment chacune d'entre elles contribue à la performance globale. Le SEM est un outil puissant qui combine l'analyse factorielle et l'analyse de régression multiple pour analyser les relations entre plusieurs variables. Cela ressemble un peu à la façon dont, dans notre vie quotidienne, nous considérons comment des facteurs tels que la posture, la confiance en soi et les compétences en matière de communication influencent collectivement les performances lors d'un entretien, par exemple. 

Explorons maintenant le SEM, ses applications et des exemples pratiques en Python. Si vous ne connaissez pas certaines des idées centrales, telles que l'idée de facteurs latents, vous pouvez également suivre notre cours sur l 'analyse factorielle.

Qu'est-ce que la modélisation par équations structurelles ?

La modélisation par équations structurelles représente les relations causales entre les variables latentes et observées. Les variables observées sont celles que nous pouvons mesurer directement. Les concepts latents sont déduits et non mesurés directement. 

Pour saisir efficacement ces relations, la SEM est divisée en deux composantes principales : le modèle de mesure et le modèle structurel. Le modèle de mesure spécifie les relations entre les variables observées et les variables latentes correspondantes, tandis que le modèle structurel spécifie les relations entre les variables latentes.

Pourquoi les chercheurs utilisent-ils la modélisation par équations structurelles ? 

Les techniques statistiques telles que la corrélation et la régression sont inefficaces pour étudier les relations complexes à plusieurs variables. Le SEM est adapté à la modélisation de concepts complexes, à multiples facettes, qui sont mesurés avec erreur. Il est également utile parce qu'il permet de spécifier un système de relations. Les méthodes traditionnelles nous aident à étudier une variable indépendante et un ensemble de prédicteurs. Bien que la corrélation ne soit pas la causalité, le SEM nous aide à comprendre la relation causale entre la variable observée et les concepts latents.

Parmi les applications du SEM, on peut citer

• Sciences sociales : Le SEM peut être utilisé pour étudier l'influence des valeurs culturelles sur le comportement humain dans différentes sociétés.
• Éducation : Le SEM peut être utilisé pour étudier l'expérience des étudiants dans les écoles supérieures. Par exemple, pour modéliser les taux d'abandon des étudiants en doctorat aux États-Unis. 
• Modélisation du risque de maladie : Le SEM peut être appliqué à la modélisation du risque de maladie afin de déterminer le risque de maladies telles que le diabète ou les maladies cardiaques.

Concepts de base de la modélisation par équations structurelles

Voici quelques-uns des concepts fondamentaux de la modélisation par équations structurelles : 

• Variables observées: Les variables observées sont directement mesurées à partir de l'étude. Les réponses aux champs du questionnaire en sont un exemple.
• Variables latentes: Les variables latentes sont déduites des variables observées dans l'étude. Par exemple, le niveau d'intelligence dans l'évaluation des résultats scolaires d'un élève.
• Variables endogènes: Elles sont également appelées variables dépendantes. Par exemple, dans y= x1 + x2 + x3, y est la variable endogène car elle dépend des valeurs de x1, x2, ..., xn.
• Variables exogènes: Il s'agit de variables indépendantes. Par exemple, le temps de sommeil d'un athlète est indépendant du type de vélo de course. 
• Modèle de mesure: mesure les relations entre les concepts latents et les variables observées. Le cadre de l'analyse factorielle confirmatoire permet de tester l'hypothèse sous-jacente du modèle de mesure.
• Modèle structurel: Ce modèle étudie les relations causales entre les concepts latents. Il est représenté sous forme de diagramme à l'aide de l'analyse de cheminement.

Hypothèses statistiques de la modélisation par équations structurelles

Bien que le SEM soit très utile pour modéliser les relations occasionnelles, il repose sur des hypothèses sous-jacentes concernant les données. Les hypothèses sont les suivantes :

1. Linéarité: Le SEM suppose des relations linéaires entre les concepts latents et les variables observées. Il n'est pas adapté aux ensembles de données non linéaires car il peut donner des résultats incorrects. 
2. Multicollinéarité: Le SEM suppose une multicolinéarité minimale entre les variables observées. Par exemple, le temps de sommeil et l'alimentation d'un concurrent peuvent être fortement corrélés. Le SEM suppose qu'il y a peu de corrélation entre ces variables.
3. Échantillonnage Hypothèses: Pour les tâches SEM, vous avez besoin d'un échantillon de taille suffisante, d'au moins 200 personnes, pour obtenir de bons résultats. Bien que vous n'ayez pas besoin de grands ensembles de données comme les LLM, un échantillon de petite taille peut donner des résultats inexacts.
4. Multivariable Normalité: Le SEM suppose que les données sont une distribution normale multivariée. Il n'est pas adapté aux données non normales. Vous pouvez effectuer des tests pour vérifier la normalité.
5. Donnéesmanquantes : SEM suppose que les données sont complètes. L'une des façons dont le SEM aborde les données manquantes consiste à supposer que les données sont manquantes au hasard. Les données manquantes peuvent interférer avec l'estimation du modèle.
6. Spécification Erreur: Le SEM suppose que le modèle défini est spécifié correctement. Il suppose que les modèles de mesure et de structure contiennent au moins toutes les variables pertinentes.

Types de modèles d'équations structurelles

Il existe différents types de modèles d'équations structurelles. Il s'agit, sans ordre particulier, de

• Analyse de cheminement: Il s'agit d'un type de SEM et d'une extension des modèles de régression qui traitent uniquement des variables observées (également connues sous le nom de prédicteurs). Les diagrammes de parcours représentent visuellement ces relations à l'aide de flèches qui indiquent la direction. 
• Analyse factorielle confirmatoire (AFC): Il s'agit d'un type de SEM utilisé pour tester la validité des modèles de mesure. Il vérifie si les données observées correspondent à un modèle prédéfini.
• Modèles structurels à variables latentes (LVSM): Il modélise les relations entre les concepts latents et les variables observées. Il modélise également la relation entre les concepts latents eux-mêmes.
• Modèles de croissance latente: Les modèles de croissance latente sont un type spécialisé de SEM qui se concentre sur la modélisation du changement dans le temps. Ils sont utilisés pour étudier les trajectoires des variables latentes (par exemple, les traits psychologiques ou les comportements) et leur évolution, en tenant compte des changements au niveau de l'individu et du groupe.

Exemple de modélisation des équations structurelles en Python

Le développement d'un modèle SEM en Python ne nécessite que quelques étapes ; nous pouvons utiliser la bibliothèque semopy pour faciliter les choses. Le tutoriel suivant suppose que vous êtes familiarisé avec la syntaxe de Python.

Installation des bibliothèques nécessaires

pip install semopy

Note: Pour les utilisateurs de macOS. Si vous rencontrez cette erreur lors de l'installation du paquet :

ExecutableNotFound: failed to execute PosixPath('dot'), make sure the Graphviz executables are on your systems' PATH

Installez graphviz via homebrew dans votre terminal

brew install graphviz

Définir les constructions

Avant de télécharger notre jeu de données et de créer notre modèle, prenons une minute pour définir toutes nos constructions. En d'autres termes, nous devons identifier les variables latentes et observées. Dans le cas de notre ensemble de données, les variables observées nous ont été fournies en tant que caractéristiques étiquetées et sont x1 à x3 et y1 à y8. Les variables latentes que nous voulons étudier portent ces noms, que nous allons expliquer : ind60, dem60, dem65. 

Variables observées

• y1Liberté de la presse, 1960

• y2Liberté de l'opposition politique, 1960

• y3L'équité des élections, 1960

• y4Efficacité de la législature élue, 1960

• y5 -y8: sont les mêmes variables que y1-y4, respectivement, mesurées en 1965

• x1Le PNB par habitant, 1960

• x2Consommation d'énergie par habitant, 1960

• x3Pourcentage de la main-d'œuvre dans l'industrie, 1960

Variables latentes

• ind60: variable latente exogène sur l'industrialisation.

• dem60: variable latente endogène sur la démocratie en 1960.

• dem65: variable latente endogène sur la démocratie en 1965.

Élaboration du modèle de mesure

L'objectif est de définir un modèle théorique pour spécifier la relation entre les concepts latents et les variables observées.

# Measurement model
ind60 =~ x1 + x2 + x3
demo60 =~ y1 + y2 + y3 + y4
dem65 =~ y5 + y6 + y7 + y8

Spécification du modèle structurel

Nous préciserons ici les relations entre les concepts latents eux-mêmes. 

# regressions
dem60 ~ ind60
dem65 ~ ind60 + dem60

Spécification des corrélations

Ici, nous voulons spécifier des variables qui sont fortement corrélées entre elles.

# Correlations
y1 ~~ y5 
y2 ~~ y4 
y2 ~~ y6 
y3 ~~ y7 
y4 ~~ y8 
y6 ~~ y5

Préparation du jeu de données

Pour ce tutoriel, nous utiliserons le jeu de données PoliticalDemocracy.csv fourni par semopy. Vous pouvez le télécharger en visitant ce dépôt GitHub.

Import pandas as pd
data = pd.read_csv('PoliticalDemocracy.csv')

Définition du modèle SEM

Nous devons combiner les définitions structurelles et de mesure dans une spécification de modèle.

# Define the SEM model specification
model_spec = """
# Measurement model
ind60 =~ x1 + x2 + x3
dem60 =~ y1 + y2 + y3 + y4
dem65 =~ y5 + y6 + y7 + y8
    
# regressions
dem60 ~ ind60
dem65 ~ ind60 + dem60
    
# Correlations
y1 ~~ y5 
y2 ~~ y4 
y2 ~~ y6 
y3 ~~ y7 
y4 ~~ y8 
y6 ~~ y5
"""

Ensuite, nous définissons le modèle et ajustons les données

import semopy
# Define the model
model = semopy.Model(model_spec)
#Fit the model
model.fit(data)
# Inspect the results
print(model.inspect())

Interprétation des résultats

Nous allons tracer le résultat du modèle pour comprendre la représentation du chemin. Le tracé sera sauvegardé sous political_sem_model.png.

semopy.semplot(model, 'political_sem_model.png')
print("SEM Model diagram saved as 'political_sem_model.png'.")
img = plt.imread('political_sem_model.png')
plt.imshow(img)
plt.axis('off')
plt.show()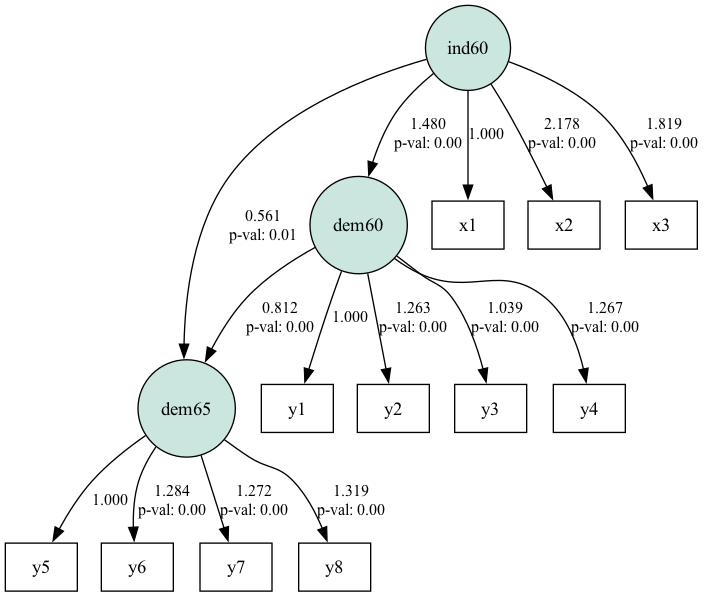

Diagramme de cheminement SEM pour l'ensemble de données sur la démocratie politique. Source : Image par l'auteur

Le diagramme montre comment le chemin relie les concepts latents (dans les cercles) et les variables observées. Les coefficients de cheminement proches de 1 ou de -1 indiquent des relations fortes entre les variables et ceux proches de 0 indiquent des relations faibles.

Les écarts types figurant dans le tableau se situent dans la fourchette. Des valeurs plus élevées peuvent indiquer une multicolinéarité ou une mauvaise spécification du modèle. Les valeurs p déterminent la signification statistique des coefficients de cheminement. Une valeur p inférieure à 0,05 indique généralement que le chemin est statistiquement significatif. Dans deux cas, la valeur p est supérieure à 0,05. 

Dans l'ensemble, les résultats montrent que ind60 influence significativement dem60, qui à son tour influence significativement dem65.

Évaluer l'adéquation du modèle

Le modèle hypothétique doit correspondre aux relations observées pour évaluer l'adéquation du modèle SEM. Différents indices d'adéquation sont utilisés pour évaluer dans quelle mesure le modèle s'adapte aux données. Voici celles qui sont le plus souvent utilisées :

• Test du chi carré: Compare la matrice de covariance observée avec la matrice de covariance implicite du modèle. Un chi-carré non significatif indique une bonne adéquation. 
• Erreur quadratique moyenne de l'approximation: Il évalue dans quelle mesure le modèle se rapproche des données, en tenant compte de la complexité du modèle. Les valeurs inférieures à 0,05 et inférieures à 0,08 sont acceptables.

Défis communs et solutions en matière de SEM

La technique de modélisation par équations structurelles pose souvent les problèmes suivants :

• Non-normalité des données: Le SEM suppose généralement que les données suivent une distribution normale. L'utilisation de données non normales peut affecter les erreurs standard, les valeurs p et les indices d'ajustement, ce qui conduit à des estimations peu fiables. Des techniques de transformation des données peuvent être appliquées pour normaliser les données.
• Données manquantes : Des données complètes sont nécessaires pour le SEM. Les données manquantes peuvent fausser les résultats. Vous pouvez vous appuyer sur des méthodes d'estimation de la vraisemblance telles que le maximum de vraisemblance à information complète (FIML) pour résoudre ce problème.
• Modèle ajusté: Lorsque le modèle hypothétique ne correspond pas aux données observées, il conduit à des interprétations erronées de la relation entre les variables. Vous pouvez procéder à des ajustements théoriques du modèle ou utiliser des indices de modification. 

Conclusion

Dans cet article, nous avons examiné en profondeur le SEM, y compris ses applications, sa mise en œuvre, ses avantages et ses limites. Le SEM est un outil puissant pour examiner les relations complexes et les interactions causales entre les variables observées et latentes. Vous devriez l'essayer en Python ou en R pour votre prochain projet d'analyse.

Si vous êtes intéressé par l'idée de la modélisation des équations structurelles mais que vous préférez R, vous pouvez suivre le cours Structural Equation Modeling with lavaan in R, qui contient des instructions détaillées étape par étape. Vous pouvez également vous lancer dans le cursus de statisticien en R. Si vous êtes attaché à Python, lisez la documentation de semopy pour plus de cas d'utilisation de SEM en Python. Enfin, si vous êtes intéressé par des modèles Python avancés qui permettent à la fois de prédire et d'expliquer, et d'explorer les idées d'architecture de modèle et de sélection de caractéristiques, essayez notre cursus de carrière Machine Learning Scientist in Python.