Curso
A classificação é um processo de duas etapas: uma etapa de aprendizagem e uma etapa de previsão. Na etapa de aprendizagem, o modelo é desenvolvido com base nos dados de treinamento fornecidos. Na etapa de previsão, o modelo é usado para prever a resposta a determinados dados. Uma árvore de decisão é um dos algoritmos de classificação mais fáceis e populares usados para entender e interpretar dados. Pode ser usado tanto para problemas de classificação quanto de regressão.
Para executar facilmente todos os códigos de exemplo deste tutorial, você pode criar gratuitamente uma pasta de trabalho do DataLab com o Python pré-instalado e contendo todos os exemplos de código. F
Torne-se um cientista de ML
O Algoritmo da Árvore de Decisão
Uma árvore de decisão é uma estrutura em forma de árvore parecida com um fluxograma, onde um nó interno representa uma característica (ou atributo), o ramo representa uma regra de decisão e cada nó folha representa o resultado.
O nó mais alto numa árvore de decisão é conhecido como nó raiz. Ele aprende a dividir com base no valor do atributo. Ele divide a árvore de um jeito recursivo, chamado particionamento recursivo. Essa estrutura tipo fluxograma te ajuda a tomar decisões. É uma visualização tipo um fluxograma que imita facilmente o pensamento humano. É por isso que as árvores de decisão são fáceis de entender e interpretar.
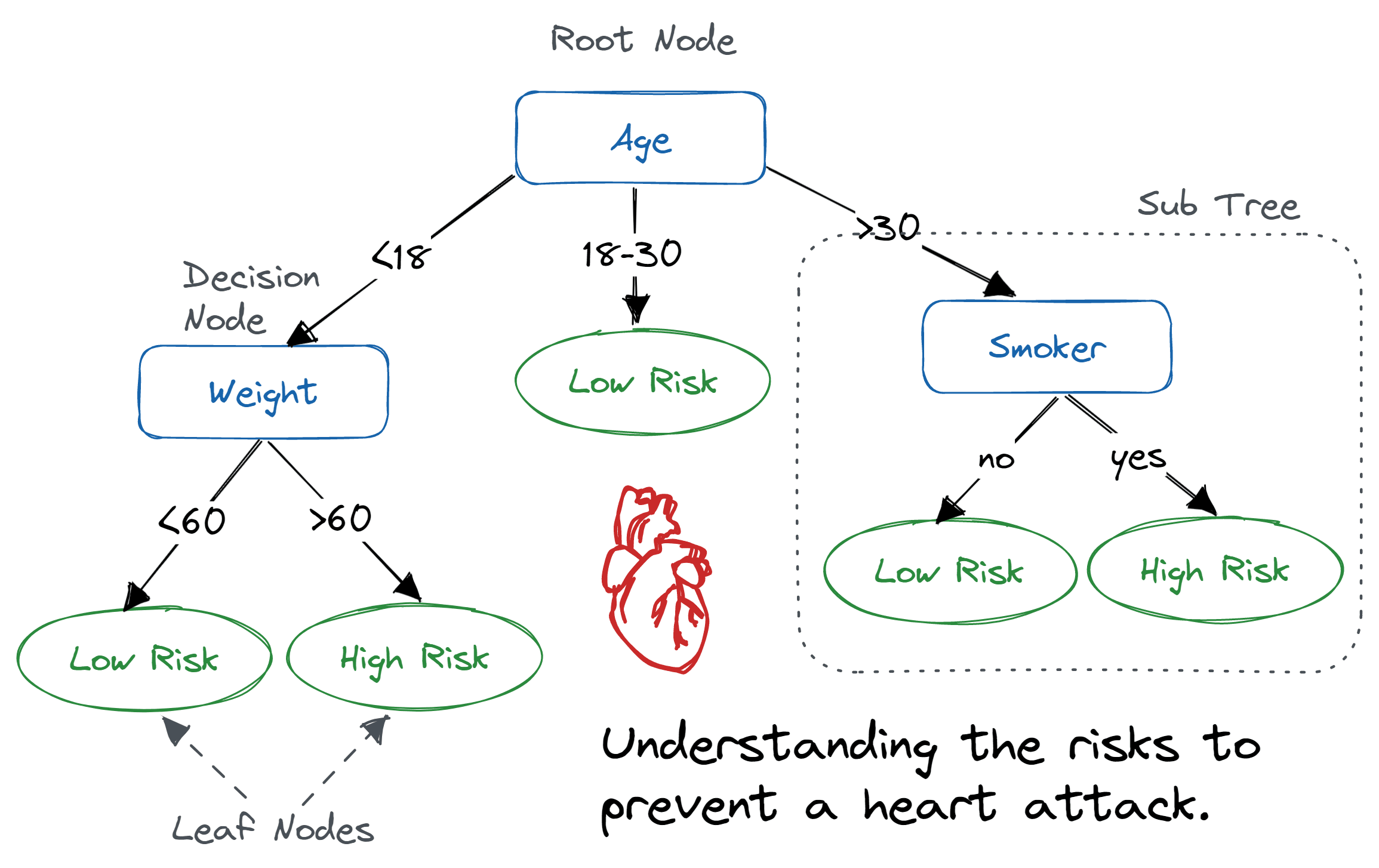
Algoritmo de árvore de decisão. Imagem de Abid Ali Awan
Uma árvore de decisão é um tipo de algoritmo de ML do tipo caixa branca. Ele compartilha a lógica interna de tomada de decisão, que não está disponível em algoritmos do tipo caixa preta, como em uma rede neural. O tempo de treinamento é mais rápido em comparação com o algoritmo de rede neural.
A complexidade temporal das árvores de decisão depende do número de registros e atributos nos dados fornecidos. A árvore de decisão é um método livre de distribuição ou não paramétrico que não depende de suposições sobre a distribuição de probabilidade subjacente dos dados. As árvores de decisão conseguem lidar com dados de alta dimensão com boa precisão.
Como funciona o algoritmo da árvore de decisão?
A ideia básica por trás de qualquer algoritmo de árvore de decisão é a seguinte:
- Escolha o melhor atributo usando as Medidas de Seleção de Atributos (ASM) para dividir os registros.
- Transforme esse atributo em um nó de decisão e divida o conjunto de dados em subconjuntos menores.
- Comece a construir a árvore repetindo esse processo recursivamente para cada filho até que uma das condições seja atendida:
- Todas as tuplas têm o mesmo valor de atributo.
- Não tem mais atributos sobrando.
- Não tem mais casos.
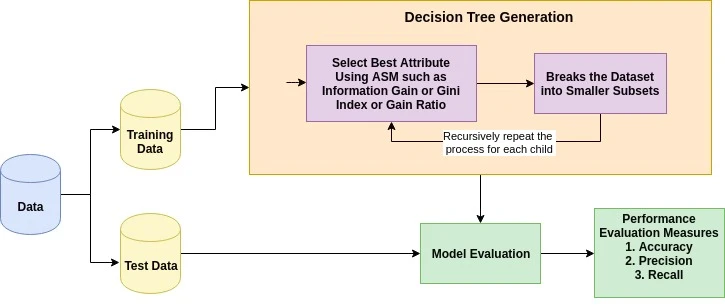
Medidas de seleção de atributos
A medida de seleção de atributos é uma forma de escolher o critério de divisão que divide os dados da melhor maneira possível. Também é conhecido como regras de divisão porque nos ajuda a determinar pontos de interrupção para tuplas em um determinado nó. O ASM dá uma classificação para cada característica (ou atributo) explicando o conjunto de dados fornecido. O atributo de melhor pontuação vai ser escolhido como um atributo de divisão (Fonte). No caso de um atributo de valor contínuo, também é preciso definir pontos de divisão para os ramos. As medidas de seleção mais populares são Ganho de Informação, Relação de Ganho e Índice de Gini.
Ganho de informação
Claude Shannon inventou o conceito de entropia, que mede a impureza do conjunto de entradas. Na física e na matemática, a entropia é a aleatoriedade ou a impureza em um sistema. Na teoria da informação, isso se refere à impureza em um grupo de exemplos. Ganho de informação é a redução da entropia. O ganho de informação calcula a diferença entre a entropia antes da divisão e a entropia média após a divisão do conjunto de dados com base nos valores de atributos fornecidos. O algoritmo da árvore de decisão ID3 (Iterative Dichotomiser) usa o ganho de informação.
Onde Pi é a probabilidade de que uma tupla qualquer em D pertença à classe Ci.
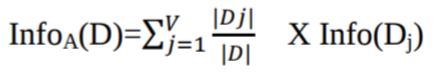
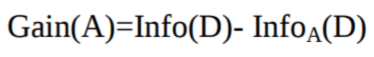
Onde:
-
Info(D)é a quantidade média de informação necessária para identificar o rótulo de classe de uma tupla emD. -
|Dj|/|D|funciona como o peso da partiçãoj. -
InfoA(D)é a informação esperada necessária para classificar uma tupla deDcom base na partição porA.
O atributo A com o maior ganho de informação, Ganho(A), é escolhido como o atributo de divisão no nó N().
Relação de ganho
O ganho de informação é tendencioso para o atributo com muitos resultados. Isso quer dizer que ele prefere o atributo com um monte de valores diferentes. Por exemplo, pense num atributo com um identificador único, como customer_ID, que não tem nenhuma informação (D) por causa da partição pura. Isso maximiza o ganho de informação e cria particionamentos inúteis.
O C4.5, uma melhoria do ID3, usa uma extensão do ganho de informação conhecida como razão de ganho. A taxa de ganho resolve o problema do viés normalizando o ganho de informação usando a Informação de Divisão. A implementação Java do algoritmo C4.5 é conhecida como J48, que está disponível na ferramenta de mineração de dados WEKA.
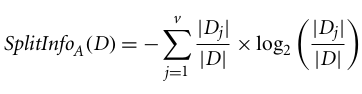
Onde:
- |Dj|/|D| é tipo o peso da j-ésima partição.
- v é o número de valores discretos no atributo A.
A taxa de ganho pode ser definida como
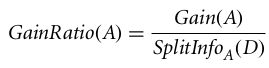
O atributo com a maior taxa de ganho é escolhido como o atributo de divisão (Fonte).
Índice de Gini
Outro algoritmo de árvore de decisão, o CART (Classification and Regression Tree), usa o método Gini para criar pontos de divisão.
Onde pi é a probabilidade de que uma tupla em D pertença à classe Ci.
O Índice de Gini considera uma divisão binária para cada atributo. Você pode calcular uma soma ponderada da impureza de cada partição. Se uma divisão binária no atributo A divide os dados D em D1 e D2, o índice de Gini de D é:
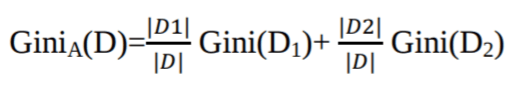
No caso de um atributo de valor discreto, o subconjunto que dá o índice de Gini mínimo para o escolhido é selecionado como um atributo de divisão. No caso de atributos com valores contínuos, a ideia é escolher cada par de valores próximos como um possível ponto de divisão, e o ponto com o menor índice de Gini é escolhido como o ponto de divisão.
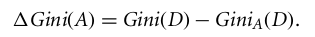
O atributo com o índice de Gini mínimo é escolhido como o atributo de divisão.
Execute e edite o código deste tutorial online
Executar códigoCriação de classificador de árvore de decisão no Scikit-learn
Importando as bibliotecas necessárias
Vamos primeiro carregar as bibliotecas necessárias.
# Load libraries
import pandas as pd
from sklearn.tree import DecisionTreeClassifier # Import Decision Tree Classifier
from sklearn.model_selection import train_test_split # Import train_test_split function
from sklearn import metrics #Import scikit-learn metrics module for accuracy calculation
Carregando dados
Vamos primeiro carregar o conjunto de dados necessário sobre diabetes entre os índios Pima usando a função de leitura de CSV do pandas. Você pode baixar o conjunto de dados do Kaggle para acompanhar.
col_names = ['pregnant', 'glucose', 'bp', 'skin', 'insulin', 'bmi', 'pedigree', 'age', 'label']
# load dataset
pima = pd.read_csv("diabetes.csv", header=None, names=col_names)
pima.head()
| grávida | glucose | bp | pele | insulina | bmi | linhagem | idade | rótulo | |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 6 | 148 | 72 | 35 | 0 | 33,6 | 0,627 | 50 | 1 |
| 1 | 1 | 85 | 66 | 29 | 0 | 26,6 | 0,351 | 31 | 0 |
| 2 | 8 | 183 | 64 | 0 | 0 | 23,3 | 0,672 | 32 | 1 |
| 3 | 1 | 89 | 66 | 23 | 94 | 28,1 | 0,167 | 21 | 0 |
| 4 | 0 | 137 | 40 | 35 | 168 | 43,1 | 2.288 | 33 | 1 |
Seleção de recursos
Aqui, você precisa dividir as colunas fornecidas em dois tipos de variáveis: variáveis dependentes (ou variáveis-alvo) e variáveis independentes (ou variáveis características).
#split dataset in features and target variable
feature_cols = ['pregnant', 'insulin', 'bmi', 'age','glucose','bp','pedigree']
X = pima[feature_cols] # Features
y = pima.label # Target variable
Dividindo dados
Pra entender o desempenho do modelo, uma boa estratégia é dividir o conjunto de dados em um conjunto de treinamento e um conjunto de teste.
Vamos dividir o conjunto de dados usando a função ` train_test_split()`. Você precisa passar três parâmetros: características, tamanho do conjunto de dados de destino e tamanho do conjunto de dados de teste.
# Split dataset into training set and test set
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=1) # 70% training and 30% test
Criando um modelo de árvore de decisão
Vamos criar um modelo de árvore de decisão usando o Scikit-learn.
# Create Decision Tree classifer object
clf = DecisionTreeClassifier()
# Train Decision Tree Classifer
clf = clf.fit(X_train,y_train)
#Predict the response for test dataset
y_pred = clf.predict(X_test)
Avaliando o modelo
Vamos ver com que precisão o classificador ou modelo consegue prever o tipo de cultivares.
A precisão pode ser calculada comparando os valores reais do conjunto de testes com os valores previstos.
# Model Accuracy, how often is the classifier correct?
print("Accuracy:",metrics.accuracy_score(y_test, y_pred))
Accuracy: 0.6753246753246753
Conseguimos uma taxa de classificação de 67,53%, o que é considerado uma boa precisão. Você pode melhorar essa precisão ajustando os parâmetros no algoritmo da árvore de decisão.
Visualizando árvores de decisão
Você pode usar a função ` export_graphviz() ` do Scikit-learn para mostrar a árvore dentro de um notebook Jupyter. Para desenhar a árvore, você também precisa instalar graphviz e pydotplus.
pip install graphviz
pip install pydotplusA função export_graphviz() transforma o classificador da árvore de decisão em um arquivo dot, e o pydotplus transforma esse arquivo dot em PNG ou em um formato que dá pra ver no Jupyter.
from sklearn.tree import export_graphviz
from sklearn.externals.six import StringIO
from IPython.display import Image
import pydotplus
dot_data = StringIO()
export_graphviz(clf, out_file=dot_data,
filled=True, rounded=True,
special_characters=True,feature_names = feature_cols,class_names=['0','1'])
graph = pydotplus.graph_from_dot_data(dot_data.getvalue())
graph.write_png('diabetes.png')
Image(graph.create_png())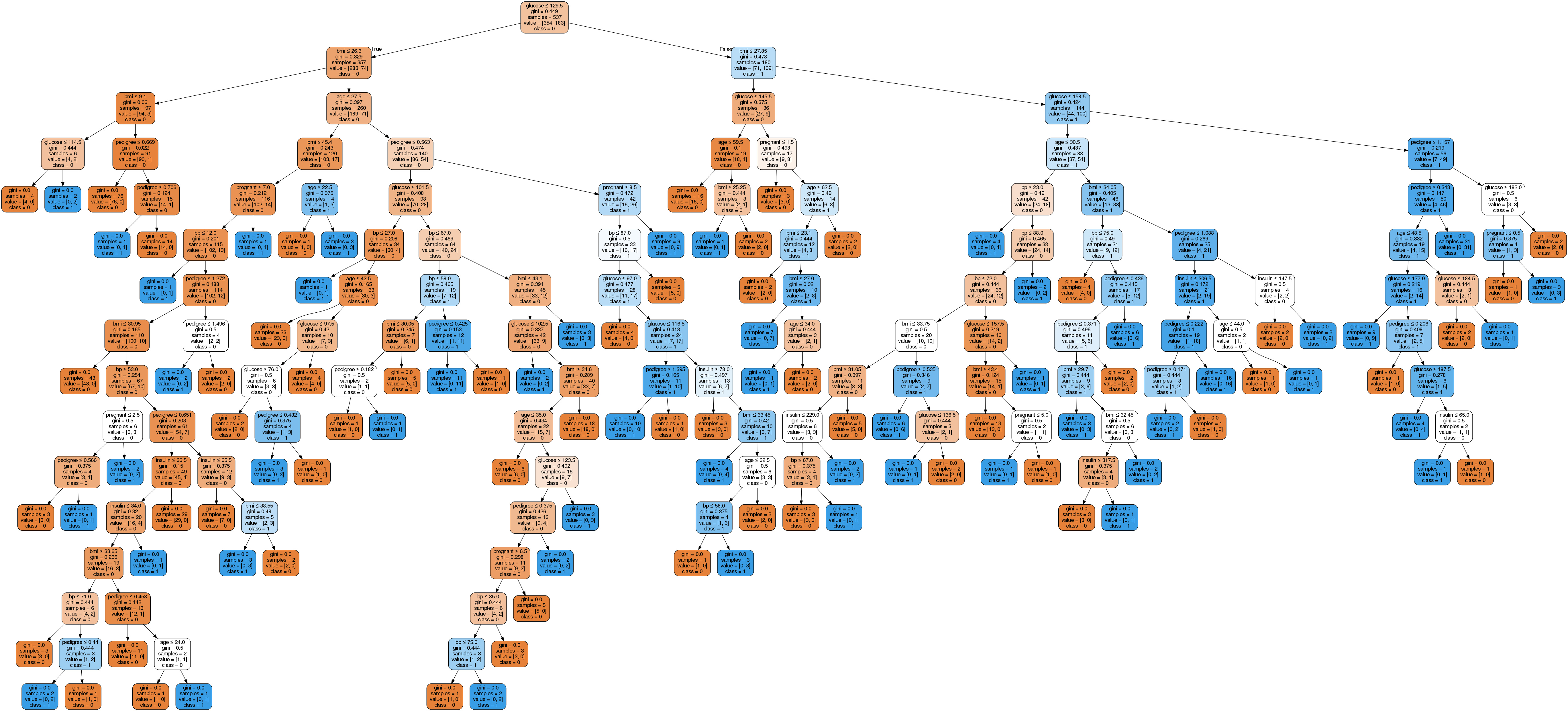
No gráfico da árvore de decisão, cada nó interno tem uma regra de decisão que divide os dados. O Gini, também chamado de índice de Gini, mede a impureza do nó. Dá pra dizer que um nó é puro quando todos os seus registros são da mesma classe. Esses nós são conhecidos como nós folha.
Aqui, a árvore resultante não foi podada. Essa árvore sem poda é inexplicável e difícil de entender. Na próxima seção, vamos otimizar isso com a poda.
Otimizando o desempenho da árvore de decisão
-
critério: opcional (padrão = “gini”) ou Escolha a medida de seleção de atributos. Esse parâmetro permite usar a medida de seleção de atributos diferentes-diferentes. Os critérios suportados são “gini” para o índice de Gini e “entropia” para o ganho de informação.
-
divisor: string, opcional (padrão = “melhor”) ou Estratégia de Divisão. Esse parâmetro permite escolher a estratégia de divisão. As estratégias suportadas são “melhor” para escolher a melhor divisão e “aleatória” para escolher a melhor divisão aleatória.
-
max_depth: int ou None, opcional (padrão=None) ou Profundidade máxima de uma árvore. A profundidade máxima da árvore. Se for None, os nós são expandidos até que todas as folhas tenham menos que min_samples_split amostras. Um valor mais alto de profundidade máxima faz com que o modelo se ajuste demais, e um valor mais baixo faz com que ele se ajuste de menos (Fonte).
No Scikit-learn, a otimização do classificador de árvore de decisão é feita só com pré-poda. A profundidade máxima da árvore pode ser usada como uma variável de controle para o pré-podar. No exemplo a seguir, você pode traçar uma árvore de decisão com os mesmos dados usando max_depth=3. Além dos parâmetros de pré-poda, você também pode tentar outras medidas de seleção de atributos, como a entropia.
# Create Decision Tree classifer object
clf = DecisionTreeClassifier(criterion="entropy", max_depth=3)
# Train Decision Tree Classifer
clf = clf.fit(X_train,y_train)
#Predict the response for test dataset
y_pred = clf.predict(X_test)
# Model Accuracy, how often is the classifier correct?
print("Accuracy:",metrics.accuracy_score(y_test, y_pred))
Accuracy: 0.7705627705627706Bem, a taxa de classificação aumentou para 77,05%, o que é uma precisão melhor do que o modelo anterior.
Vamos deixar nossa árvore de decisão um pouco mais fácil de entender usando o seguinte código:
from six import StringIO
from IPython.display import Image
from sklearn.tree import export_graphviz
import pydotplus
dot_data = StringIO()
export_graphviz(clf, out_file=dot_data,
filled=True,
rounded=True,
special_characters=True,
feature_names=feature_cols,
class_names=['0','1'])
graph = pydotplus.graph_from_dot_data(dot_data.getvalue())
graph.write_png('diabetes.png')
Image(graph.create_png())Aqui, fizemos o seguinte:
-
Importou as bibliotecas necessárias.
-
Criei um objeto
StringIOchamadodot_datapara guardar a representação textual da árvore de decisão. -
Exportou a árvore de decisão para o formato
dotusando a funçãoexport_graphvize gravou a saída no bufferdot_data. -
Criou um objeto gráfico
pydotplusa partir da representação no formatodotda árvore de decisão armazenada no bufferdot_data. -
Escreva o gráfico gerado em um arquivo PNG chamado “diabetes.png”.
-
Mostrou a imagem PNG gerada da árvore de decisão usando o objeto
Imagedo móduloIPython.display.
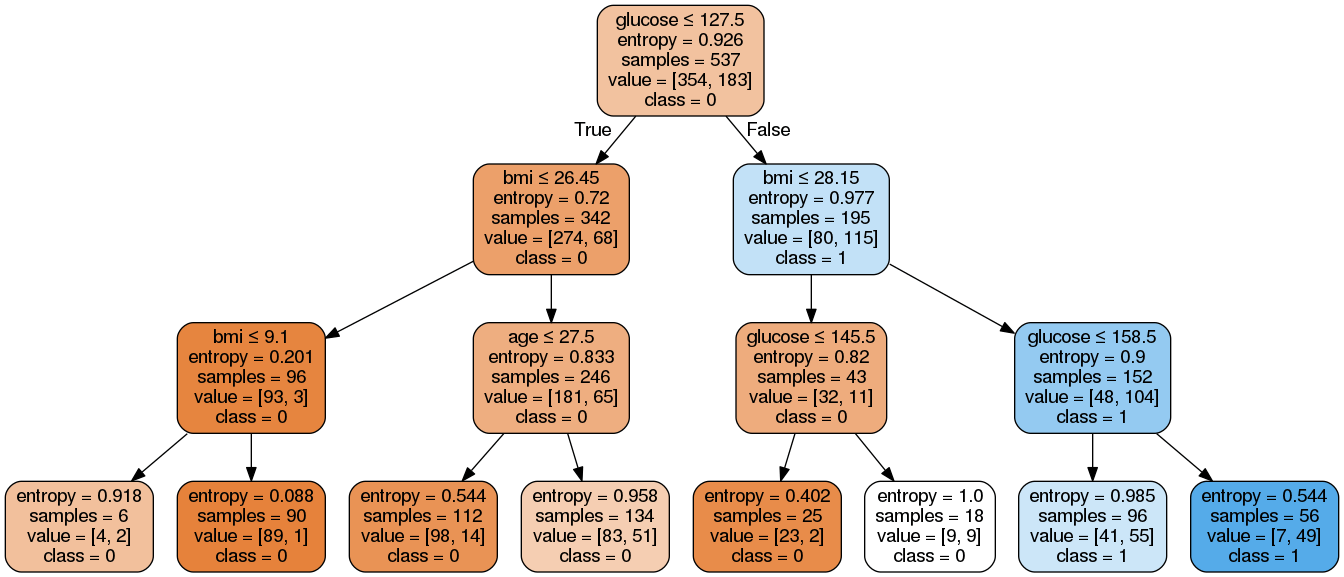
Como você pode ver, esse modelo simplificado é menos complicado, mais fácil de explicar e entender do que o gráfico anterior da árvore de decisão.
Prós e contras da árvore de decisão
Agora que você criou e otimizou um classificador de árvore de decisão, vamos dar uma pausa para avaliar alguns dos pontos fortes e limitações do algoritmo de forma mais geral. Entender as vantagens e desvantagens ajuda você a decidir quando as árvores de decisão são a escolha certa.
| Vantagens | Desvantagens |
|---|---|
| Fácil de entender e visualizar | Sensível a dados ruidosos e pode sobreajustar |
| Pode capturar facilmente padrões não lineares | Pequenas variações nos dados podem resultar em árvores muito diferentes. |
| Precisa de um pré-processamento mínimo dos dados (não precisa normalizar as colunas) | Viciado com conjuntos de dados desequilibrados (recomenda-se o equilíbrio) |
| Útil para engenharia de recursos (previsão de valores ausentes, seleção de variáveis) | |
| Sem suposições sobre a distribuição dos dados (não paramétrica) |
Vale lembrar que algumas desvantagens, como a instabilidade da variância, podem ser amenizadas com métodos de conjunto, como algoritmosde baggingeboosting.
Árvore de decisão vs. Decisão difícil
Embora tenhamos trabalhado com árvores de decisão completas ao longo deste tutorial, vale a pena entender uma variante mais simples chamada tronco de decisão. Um tronco de decisão é basicamente uma árvore de decisão com profundidade máxima de um, ou seja, tem só uma divisão no nó raiz e dois nós folha.
| Aspecto | Árvore de decisão | Decisão difícil |
|---|---|---|
| Profundidade | Pode ter qualquer profundidade (controlada por max_depth parâmetro) |
Sempre profundidade de 1 (apenas uma divisão) |
| Complexidade | Pode modelar relações complexas e não lineares | Modelos apenas com limites de decisão simples e lineares |
| Caso de uso | Classificador independente para problemas complexos | Usado principalmente como um aluno fraco em métodos de conjunto |
| Precisão | Geralmente maior precisão como modelo independente | Precisão menor, mas eficaz quando combinado |
| Interpretabilidade | Diminui com a profundidade (como vimos com nossa árvore não podada) | Super simples e fácil de entender |
Os troncos de decisão raramente são usados como classificadores independentes por causa da sua simplicidade. Mas eles podem ter um papel nos métodos de conjunto, especialmente o AdaBoost usa stumps de decisão como aprendizes fracos que são combinados para criar um classificador forte, oureforço de gradiente, porque os stumps podem ser usados como aprendizes básicos no processo de reforço.
Você pode criar um stump de decisão no Scikit-learn simplesmente definindo um max_depth=1:
# Create a Decision Stump
stump = DecisionTreeClassifier(max_depth=1)
stump = stump.fit(X_train, y_train)Conclusão
Parabéns, você chegou ao fim deste tutorial!
Neste tutorial, você aprendeu vários detalhes sobre árvores de decisão: como elas funcionam, medidas de seleção de atributos como ganho de informação, taxa de ganho e índice de Gini, construção de modelos de árvores de decisão, visualização e avaliação de um conjunto de dados sobre diabetes usando o pacote Scikit-learn do Python. Também falamos sobre os prós, contras e como melhorar o desempenho da árvore de decisão usando o ajuste de parâmetros.
Espero que agora você consiga usar o algoritmo da árvore de decisão para analisar seus próprios conjuntos de dados.
Se você quiser saber mais sobre machine learning em Python, faça nosso curso Machine Learning com Modelos Baseados em Árvores em Python. Além disso, dá uma olhada no nosso tutorial Kaggle sobre o “ ”: Seu primeiro modelo de machine learning.
Obtenha a certificação para a função de cientista de dados dos seus sonhos
Nossos programas de certificação ajudam você a se destacar e a provar que suas habilidades estão prontas para o trabalho para possíveis empregadores.
Perguntas frequentes sobre classificação por árvore de decisão
Quais são os casos de uso mais comuns para a classificação por árvore de decisão?
A classificação por árvore de decisão é bem comum em várias áreas, tipo finanças para pontuação de crédito, saúde para diagnóstico de doenças, marketing para segmentação de clientes e muito mais. Ajuda na tomada de decisões, dividindo os dados em subconjuntos com base em diferentes critérios.
Como posso evitar o sobreajuste ao usar árvores de decisão?
O sobreajuste pode ser evitado podando a árvore, definindo uma profundidade máxima, usando um número mínimo de amostras necessárias para dividir um nó interno e usando um número mínimo de amostras necessárias para estar em um nó folha. A validação cruzada também pode ajudar a ajustar esses parâmetros de forma eficaz.
Qual é a diferença entre uma árvore de decisão e uma floresta aleatória?
Uma árvore de decisão é uma estrutura única em forma de árvore usada para classificação ou regressão. Já uma floresta aleatória é um conjunto de várias árvores de decisão, que melhora a precisão das previsões e controla o sobreajuste, calculando a média dos resultados de várias árvores.
Como faço pra lidar com valores que estão faltando no meu conjunto de dados quando uso árvores de decisão?
As árvores de decisão podem lidar com valores ausentes usando divisões substitutas ou substituindo os valores ausentes pelo valor mais frequente ou pela média/moda da característica. O Scikit-learn também oferece métodos como o SimpleImputer para preencher valores ausentes antes de treinar o modelo.
Quais são as vantagens de usar o Scikit-learn pra construir modelos de árvores de decisão?
O Scikit-learn oferece uma ferramenta simples e eficiente para mineração e análise de dados, incluindo classificadores de árvores de decisão. Ele oferece vários recursos, como fácil integração, documentação abrangente, suporte para várias métricas e ajuste de parâmetros, além de métodos para visualizar árvores de decisão, tornando-o uma escolha popular entre os profissionais de machine learning.

