Curso
Você pode notar a curva de sino, que tem vários nomes, como distribuição normal ou distribuição gaussiana, em praticamente todos os lugares, especialmente se você tiver interesse em estatística ou ciência de dados. Parece, mas não é um acidente da natureza: Acontece que muito do que medimos é o resultado de muitos fatores pequenos somados, o que sugere a presença de um modelo aditivo subjacente. O teorema do limite central explica o motivo: Quando uma variável é influenciada por muitos fatores pequenos e independentes, a soma dessas variáveis tende a seguir uma distribuição normal, independentemente das distribuições originais de onde vieram.
Ao transformar qualquer distribuição normal em uma forma especial chamada de distribuição normal padrão, podemos aproveitar a presença desse modelo aditivo e dar um passo adiante, padronizando essa distribuição para torná-la ainda mais útil em contextos específicos. Exploraremos como a distribuição normal padrão é usada para calcular probabilidades, fazer inferências estatísticas e aplicar testes estatísticos usando propriedades bem estabelecidas da distribuição. Ao final deste artigo, você saberá claramente o que é a distribuição normal padrão, por que tomamos a medida adicional de padronizá-la e como tudo isso se relaciona com a variabilidade, a probabilidade e o teste de hipóteses. Ao final, espero que você também se inscreva em nosso curso Introdução à estatística em R ou em nosso programa de habilidades Inferência estatística em R para continuar a desenvolver as ideias deste artigo.
O que é a distribuição normal padrão?
A distribuição normal padrão é uma forma específica da distribuição normal em que a média é zero e o desvio padrão é um. Também devemos dizer que a distribuição é simétrica e que as probabilidades de determinados valores diminuem simetricamente à medida que você se afasta do centro.

Imagem "Distribuição Normal Padrão" de Dall-E
Entendendo as equações da distribuição normal padrão
Vamos examinar um pouco mais de perto os aspectos matemáticos da distribuição normal padrão.
O PDF da distribuição normal padrão
Se você não estiver familiarizado com a ideia de uma função de densidade de probabilidade (PDF), saiba que ela descreve como as probabilidades são distribuídas entre os valores possíveis de uma variável aleatória contínua. Toda distribuição de probabilidade contínua, como a distribuição exponencial, a distribuição t ou a distribuição de Cauchy, tem sua própria função de densidade de probabilidade que define a curva. A PDF da distribuição normal padrão é definida aqui: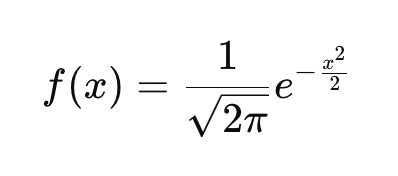
Essa função garante que a área sob a curva se integre a 1. Se você observar a equação e inserir diferentes valores de x, obterá a altura da curva nesses pontos. Na equação:
- x representa qualquer número real e é a variável de entrada para a função. Ele aparece no expoente da função, que é -x2/2. Isso controla a forma da curva.
- Como x2 é sempre não negativo e há um sinal negativo na frente, o expoente é sempre negativo ou zero.
- No caso específico em que x=0, o expoente é o maior, fazendo com que f(x) atinja seu pico.
- Se x se afastar de 0 na direção positiva ou negativa, x2 aumentará, tornando o expoente mais negativo. Umexpoente mais negativo resulta em um valor de função menor, o que significa que, juntamente com as outras coisas que dissemos, a f(x) diminui simetricamente em ambos os lados de x=0.
- A base do expoente, que é o número de Euler, garante o rápido decaimento da função à medida que x se afasta de zero em qualquer direção.
- A constante 1/√(2π) garante que a área total sob a curva seja igual a 1.
A CDF da distribuição normal padrão
Diferentemente do PDF, que fornece a probabilidade relativa de valores diferentes, o CDF informa a você a probabilidade de uma variável ser menor ou igual a um determinado valor. Assim como a PDF, toda distribuição de probabilidade contínua tem sua própria CDF.
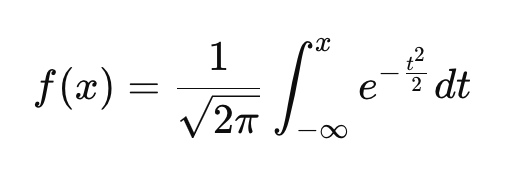
Essa equação é um pouco mais complicada, mas podemos trabalhar com ela:
- A integral significa que, em vez de fornecer a altura da curva em x, o CDF nos informa a probabilidade total de -∞ a x.
- Quando x→-∞, o CDF se aproxima de 0.
- Quando x=0 a CDF é 0,5uma vez que a distribuição é simétrica e metade da probabilidade está à esquerda de zero.
- Como x→∞o CDF se aproxima de 1.
Por que nos importamos com a distribuição normal padrão
Nosso guia sobre a distribuição gaussiana tem algumas boas ideias sobre quando você pode querer adequar seus dados a uma distribuição normal. Mas, às vezes, você pode querer transformar seus dados em um padrão normal específico. Aqui estão alguns motivos comuns para isso:
A normal padrão é usada em testes de hipóteses
Uma distribuição normal padrão torna nossos dados mais comparáveis e utilizáveis com determinados métodos estatísticos. Ao converter os dados em escores Z, podemos comparar observações em diferentes distribuições normais. Em particular, ele forma a base dos testes Z, que usamos quando queremos determinar se a média de uma amostra difere significativamente da média de uma população.
O teste t, por outro lado, usa o desvio padrão da amostra como uma estimativa do desvio padrão da população, e é por isso que ele se baseia na distribuição t, que tem caudas mais pesadas do que a distribuição normal padrão. Leia nosso tutorial T-test vs. T-test. Z-test: When to Use Each, que fala sobre assuntos como variância da população e da amostra.
A normal padrão compara os dados em uma escala comum
Como diferentes conjuntos de dados e variáveis podem ter unidades e escalas diferentes, as comparações diretas podem ser difíceis. Mas quando você os converte em escores Z, subtraindo a média e dividindo pelo desvio padrão, é fácil fazer comparações entre diferentes distribuições. Quando aplicado a um conjunto de dados normalmente distribuído, isso resulta em uma distribuição normal padrão. Por exemplo, a conversão das pontuações do SAT e do GRE, que eu espero que sejam normalmente distribuídas, em pontuações Z nos permite comparar o desempenho do aluno em relação às suas respectivas populações de testes.
O padrão normal é usado no controle de qualidade
Esse padrão normal é conhecido por ser importante no monitoramento da qualidade do produto na fabricação. Observando atentamente as probabilidades, os fabricantes podem determinar se as flutuações na qualidade se devem à variação aleatória ou a algum outro problema subjacente. Isso está relacionado ao teste de hipóteses, que mencionamos anteriormente, e também a uma tabela de pontuação Z, sobre a qual falaremos a seguir.
A normal padrão é usada em modelagem estatística
A distribuição normal padrão desempenha um papel na avaliação de erros em modelos como regressão linear e previsão de séries temporais. Nesses modelos, presumimos que os resíduos, que são as diferenças entre os valores observados e previstos, não apenas seguem uma distribuição normal, mas também podem ser padronizados para seguir uma distribuição normal padrão.
Na regressão linear, os resíduos padronizados são resíduos que foram convertidos em valores padronizados, o que nos permite medir o quão extremo é um erro em unidades de desvio padrão, o que pode facilitar a detecção de outliers. Isso é útil porque a heterocedasticidade nos resíduos, que pode não ser óbvia nos preditores do modelo, pode distorcer a interpretação dos resíduos.
Na análise de séries temporais, supõe-se com frequência que os erros de previsão sigam uma distribuição normal padrão quando devidamente padronizados. Isso é importante para a construção de intervalos de previsão. Muitos modelos de séries temporais, como o ARIMA, dependem de quantis normais padrão para definir os limites de confiança em torno das previsões. Também, na decomposição de séries temporais, o componente restante, que capta as flutuações irregulares, costuma ser distribuído normalmente. Se você padronizar esse componente restante, poderá encontrar a probabilidade de valores extremos em sua série temporal que você sabe que não são o resultado do ciclo de tendência ou da sazonalidade. Nosso curso Forecasting in R ensinará a você esses tipos de técnicas.
A normal padrão é usada no machine learning
Muitos algoritmos de machine learning funcionam melhor quando os dados estão em uma escala padrão. Estou pensando em regressão logística, agrupamento k-means e redes neurais.
Também estou pensando na análise de componentes principais, que é frequentemente usada como uma técnica de pré-processamento. No PCA, queremos que nossos recursos de entrada tenham média zero e variância unitária para ajudar o a evitar que recursos com valores grandes dominem. Uma etapa comum de pré-processamento é padronizar os dados subtraindo a média e dividindo-a pelo desvio padrão. Isso garante que cada recurso tenha média zero e variância unitária, mas devemos deixar claro que isso não impõe a normalidade. Entretanto, em alguns casos, espero que os dados transformados se aproximem da normalidade se a distribuição original já estiver próxima da normalidade.
A normal padrão é usada para cálculos de probabilidade
A função de distribuição cumulativa da distribuição normal padrão, sobre a qual falamos anteriormente, é bem tabulada, ou seja, pré-calculada e organizada em tabelas amplamente disponíveis, o que facilita os cálculos de probabilidade, pois você só precisa usar a tabela para procurar o valor correto.
Por exemplo, para descobrir a probabilidade de que uma altura escolhida aleatoriamente seja inferior a 1,80 m, padronizamos a altura usando a distribuição normal da população e procuramos o escore Z em uma tabela normal padrão. Coloquei uma versão da tabela normal padrão no final deste artigo, caso você precise usá-la.
Transformações para alinhar dados com a distribuição normal padrão
As transformações podem ajudar a remodelar os dados em uma distribuição normal padrão. Em termos gerais, esse seria um processo em duas partes. Primeiro, remodelamos nossos dados para que se tornem normais e, em seguida, realizamos a padronização da pontuação Z.
Como observação, você normalmente não aplicaria a padronização do escore Z como a primeira etapa, pois os valores extremos podem distorcer o desvio padrão, já que a média e o desvio padrão são sensíveis a valores discrepantes. Além disso, algumas transformações exigem dados positivos. Se você aplicar a padronização do escore Z primeiro, os valores centrados na média poderão incluir números negativos, o que pode causar problemas para transformações que só funcionam com valores positivos. Estou pensando especificamente em logaritmos. Portanto, é melhor você seguir na ordem: etapa 1, depois etapa 2.
Etapa 1: Transformar os dados para que se tornem normais
Algumas ideias de transformação que você pode usar incluem:
Transformação de log para dados distorcidos
Quando os dados são positivamente distorcidos, uma transformação de log pode ajudar a normalizá-los. Por exemplo, a aplicação do logaritmo a valores brutos comprime valores grandes, reduzindo a inclinação e criando uma distribuição mais simétrica.
Transformação de raiz quadrada para dados de contagem
Para dados de contagem ou conjuntos de dados moderadamente inclinados, podemos tentar uma transformação de raiz quadrada. Esse método reduz a variabilidade e, ao mesmo tempo, mantém uma estrutura mais simétrica, aproximando os dados da forma de curva de sino.
Transformação Box-Cox para ajustes flexíveis
A transformação Box-Cox vai um passo além, adaptando a transformação aos dados. Seu parâmetro λ determina a fórmula exata aplicada, tornando-o altamente versátil para alinhar os dados com as propriedades da distribuição normal padrão. O Feature Engineering in R mostrará a você o Box-Cox, entre muitos outros métodos importantes e úteis.
Etapa 2: Realizar a padronização do escore Z
Após a aplicação de uma transformação, os dados podem ser padronizados para se ajustarem à distribuição normal padrão. Isso ajusta os dados para que tenham uma média de zero e um desvio padrão de um. A fórmula do escore Z é a seguinte:
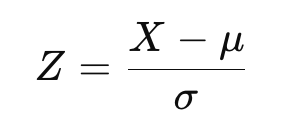
onde X são os dados transformados, μ é a média e σ é o desvio padrão.
Agora, se você estiver familiarizado com a distinção entre o escore Z da população e o escore Z da amostra, conforme abordamos em nosso programa Inferência estatística em R, talvez reconheça a equação acima como a equação para um escore Z da população. Se você estiver trabalhando com uma amostra em vez de toda a população, estimaremos a média e o desvio padrão:
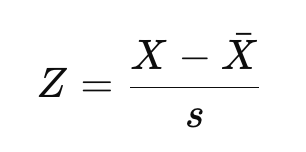
Aqui, X-bar é a média da amostra e s é o desvio padrão da amostra.
O resultado seria o mesmo se você usasse a média e o desvio padrão do novo conjunto de dados normalizado. Mas, às vezes, os pesquisadores podem estar interessados em comparar os dados em relação a uma população de referência maior, usando algum tipo de média de referência e desvio padrão.
Imagine analisar um conjunto de dados de renda, que seria inclinado para a direita, e fazer uma transformação de log para normalizá-lo. Você pode usar a transformação de log para normalizar. Então, imagine também que queremos comparar as rendas em relação às referências nacionais e, nesse caso, usaríamos a média e o desvio padrão nacionais em vez dos da nossa amostra para calcular os escores Z. O objetivo aqui seria permitir uma comparação significativa entre conjuntos de dados ou estudos.
Então, basicamente, se você estiver usando uma amostra, tecnicamente obterá uma aproximação normal padronizada em vez da distribuição normal padrão teórica exata. Acho que é uma distinção que vale a pena esclarecer, mesmo que a diferença seja pequena para grandes conjuntos de dados.
Visualização da distribuição normal padrão
Aqui está uma maneira de criar uma distribuição normal padrão teórica na linguagem de programação R. Nesse código, também adicionei linhas verticais para as pontuações padrão, também conhecidas como pontuações Z, que é uma forma de nos informar, para qualquer valor determinado, quantos desvios padrão acima ou abaixo da média da população está o nosso valor .
install.packages("ggplot2")
library(ggplot2)
ggplot(data.frame(x = c(-4, 4)), aes(x)) +
stat_function(fun = dnorm, geom = "area", fill = '#ffe6b7', color = 'black', alpha = 0.5, args = list( mean = 0, sd = 1)) +
labs(title = "Standard Normal Distribution", subtitle = "Standard Deviations and Z-Scores") +
theme(plot.title = element_text(hjust = 0.5, face = "bold")) +
theme(plot.subtitle = element_text(hjust = 0.5)) +
geom_vline(xintercept = 1, linetype = 'dotdash', color = "black") +
geom_vline(xintercept = -1, linetype = 'dotdash', color = "black") +
geom_vline(xintercept = 2, linetype = 'dotdash', color = "black") +
geom_vline(xintercept = -2, linetype = 'dotdash', color = "black") +
geom_vline(xintercept = 3, linetype = 'dotdash', color = "black") +
geom_vline(xintercept = -3, linetype = 'dotdash', color = "black") +
geom_text(aes(x=1, label="\n 1 σ", y=0.125), colour="#376795", angle=90, text=element_text(size=11)) +
geom_text(aes(x=2, label="\n 2 σ", y=0.125), colour="#376795", angle=90, text=element_text(size=11)) +
geom_text(aes(x=3, label="\n 3 σ", y=0.125), colour="#376795", angle=90, text=element_text(size=11)) +
geom_text(aes(x=-1, label="\n-1 σ", y=0.125), colour="#376795", angle=90, text=element_text(size=11)) +
geom_text(aes(x=-2, label="\n-2 σ", y=0.125), colour="#376795", angle=90, text=element_text(size=11)) +
geom_text(aes(x=-3, label="\n-3 σ", y=0.125), colour="#376795", angle=90, text=element_text(size=11))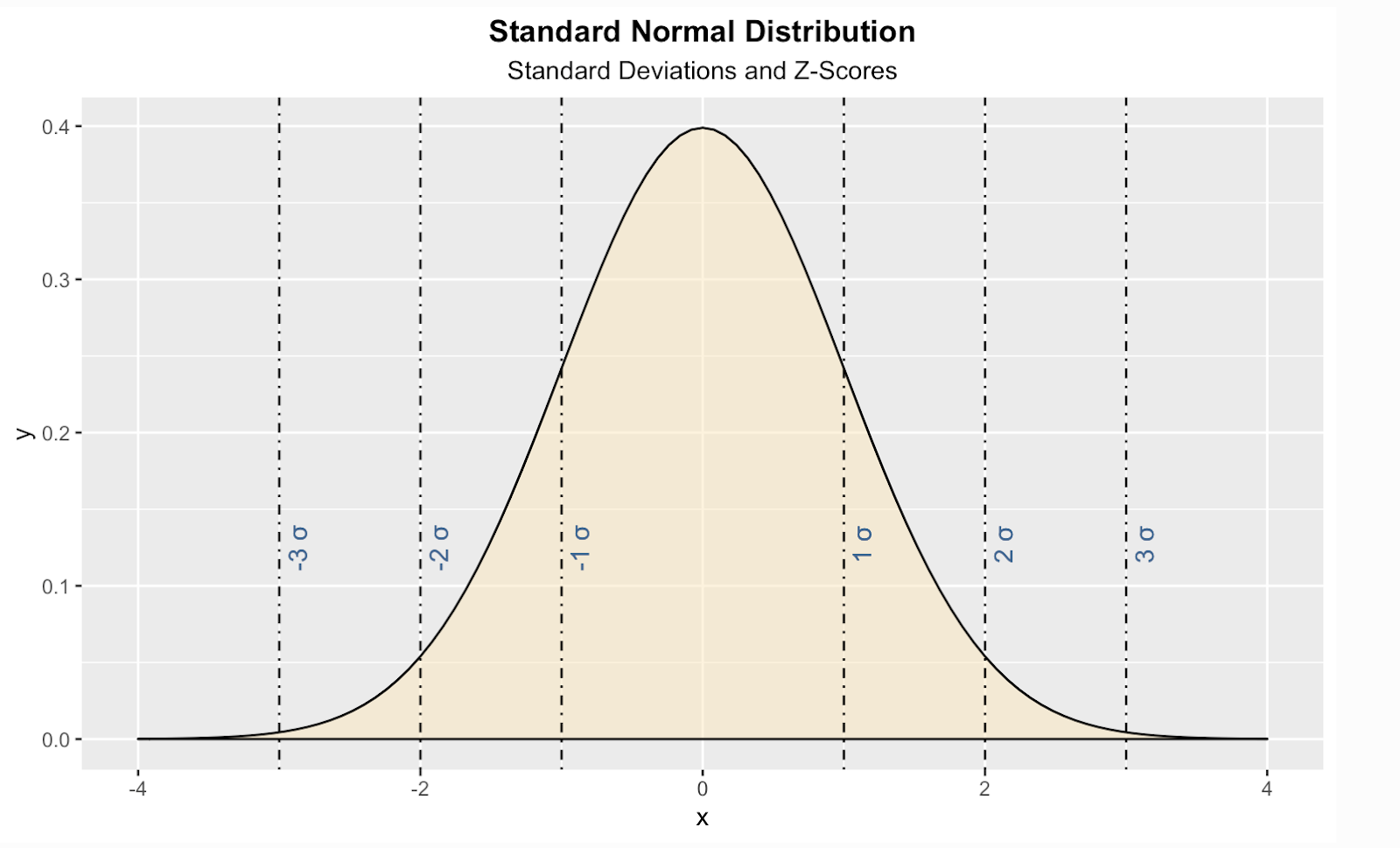
Você deve saber que existem algumas distribuições semelhantes que podem se parecer com a normal padrão, mas não são:
| Distribuição | Por que não é o padrão normal |
|---|---|
| Distribuição t | Caudas um pouco mais pesadas, dependendo dos graus de liberdade |
| Distribuição logística | Caudas um pouco mais pesadas do que o normal, formato diferente |
| Distribuição de Laplace | Pico mais nítido, caudas mais pesadas, decaimento exponencial |
A distribuição normal padrão e a tabela normal padrão
Agora, deixe-me voltar a algo que mencionei anteriormente: a ideia de uma tabela normal padrão, também chamada de tabela de pontuação Z, ou tabela Z, que é usada para encontrar probabilidades cumulativas para uma pontuação Z, que representa o número de desvios padrão de um valor em relação à média em uma distribuição normal padrão. Essa tabela é comumente usada em estatística para testes de hipóteses, intervalos de confiança e cálculos de probabilidade. A ideia aqui é que, em vez de calcular as probabilidades manualmente, você pode consultar a tabela para determinar rapidamente a proporção de valores que estão abaixo de um determinado escore Z.
Você precisa de um pouco de prática para ler a tabela, e às vezes as tabelas são diferentes umas das outras. Aqui, você o vê estruturado em um formato bidimensional. O objetivo é facilitar a busca de probabilidades para escores Z quando você trabalha com casas decimais. Nesse caso, a coluna mais à esquerda contém o número inteiro e a primeira casa decimal do escore Z. A linha superior representa a segunda casa decimal. Para encontrar a probabilidade associada a um escore Z específico, localize a linha correspondente à primeira parte do escore Z e, em seguida, encontre a coluna que corresponde à segunda casa decimal. O valor na interseção dessa linha e coluna é a probabilidade cumulativa, ou seja, a proporção de pontos de dados que estão abaixo desse escore Z.
É melhor você mostrar um exemplo: Por exemplo, suponha que você calcule um escore Z de 0,32 para a pontuação do teste de um aluno. Isso significa que a pontuação está 0,32 desvios-padrão acima da média. Agora, vamos usar a tabela Z para descobrir a probabilidade de que um valor selecionado aleatoriamente seja menor que essa pontuação Z.
- Etapa 1: Localize a linha para 0,3.
- Etapa 2: Localize a coluna para 0,02.
- Etapa 3: Veja ainterseção da linha para 0,3 e a coluna para 0,02. O valor nessa posição é 0,6915.
A probabilidade cumulativa de Z = 0,32 é 0,6554, o que significa que 65,54% dos valores em uma distribuição normal padrão são menores que 0,32 desvios padrão acima da média. Se você precisar determinar a probabilidade de um valor ser maior que um determinado escore Z, subtraia o valor da tabela de 1 antes de encontrar a linha e a coluna.
| Z | 0.01 | 0.02 | 0.03 | 0.04 | 0.05 | 0.06 | 0.07 | 0.08 | 0.09 |
|---|---|---|---|---|---|---|---|---|---|
| 0.1 | 0.5793 | 0.6179 | 0.6554 | 0.6915 | 0.7257 | 0.7580 | 0.7881 | 0.8159 | 0.8413 |
| 0.2 | 0.6179 | 0.6554 | 0.6915 | 0.7257 | 0.7580 | 0.7881 | 0.8159 | 0.8413 | 0.8643 |
| 0.3 | 0.6554 | 0.6915 | 0.7257 | 0.7580 | 0.7881 | 0.8159 | 0.8413 | 0.8643 | 0.8849 |
| 0.4 | 0.6915 | 0.7257 | 0.7580 | 0.7881 | 0.8159 | 0.8413 | 0.8643 | 0.8849 | 0.9032 |
| 0.5 | 0.7257 | 0.7580 | 0.7881 | 0.8159 | 0.8413 | 0.8643 | 0.8849 | 0.9032 | 0.9192 |
| 0.6 | 0.7580 | 0.7881 | 0.8159 | 0.8413 | 0.8643 | 0.8849 | 0.9032 | 0.9192 | 0.9332 |
| 0.7 | 0.7881 | 0.8159 | 0.8413 | 0.8643 | 0.8849 | 0.9032 | 0.9192 | 0.9332 | 0.9452 |
| 0.8 | 0.8159 | 0.8413 | 0.8643 | 0.8849 | 0.9032 | 0.9192 | 0.9332 | 0.9452 | 0.9554 |
| 0.9 | 0.8413 | 0.8643 | 0.8849 | 0.9032 | 0.9192 | 0.9332 | 0.9452 | 0.9554 | 0.9641 |
| 1.0 | 0.8643 | 0.8849 | 0.9032 | 0.9192 | 0.9332 | 0.9452 | 0.9554 | 0.9641 | 0.9713 |
Conclusão
Espero que você tenha gostado dessa exploração da distribuição normal padrão. Continue aprendendo conosco aqui no DataCamp. Mencionei nosso curso Introduction to Statistics in R e nosso programa de habilidades Statistical Inference in R. Mas se você preferir Python, nosso curso Statistical Thinking in Python e nosso curso Experimental Design in Python são ótimas opções.

Perguntas frequentes sobre a distribuição normal padrão
Como a distribuição normal padrão é diferente de uma distribuição normal?
A distribuição normal padrão é um caso específico da distribuição normal em que a média é 0 e o desvio padrão é 1. Essa padronização facilita os cálculos de probabilidade e as comparações entre conjuntos de dados.
A subtração da média e a divisão pelo desvio padrão criam uma distribuição normal padrão?
A subtração da média e a divisão pelo desvio padrão transformam um conjunto de dados em um formato padronizado, mas não criam necessariamente uma distribuição normal padrão, a menos que os dados originais tenham sido distribuídos normalmente.
Qual é a relação entre a distribuição normal padrão e o teorema do limite central?
O teorema do limite central afirma que a soma de muitas variáveis aleatórias independentes e identicamente distribuídas tende a seguir uma distribuição normal, que pode ser padronizada para a forma normal padrão.
O que representa um escore Z na distribuição normal padrão?
Um escore Z nos informa quantos desvios padrão um valor tem em relação à média. Um escore Z positivo significa que o valor está acima da média, enquanto um escore Z negativo significa que está abaixo.
Como a distribuição normal padrão se relaciona com os intervalos de confiança?
Os intervalos de confiança usam os escores Z para determinar os intervalos de probabilidade para estimar os parâmetros da população. Por exemplo, um intervalo de confiança de 95% corresponde a escores Z de aproximadamente ±1,96.

