Singuläre Matrix: Wichtige Konzepte und Beispiele in der Datenwissenschaft

Eine singuläre Matrix ist eine quadratische Matrix, die nicht invertiert werden kann, d.h. sie hat keine multiplikative Inverse. Dieses grundlegende Konzept der linearen Algebra hat einen immensen Einfluss auf die Anwendungen der Datenwissenschaft, von Algorithmen für maschinelles Lernen bis hin zur numerischen Stabilität von Berechnungsmethoden.

In diesem Artikel definieren wir, was eine Matrix singulär macht und untersuchen ihre mathematischen Eigenschaften und Merkmale. Anschließend werden wir Methoden zur Erkennung singulärer Matrizen untersuchen. Wir werden verstehen, was sie in der Datenwissenschaft wirklich bedeuten und lernen, wie wir sie effektiv nutzen können.

Was ist eine singuläre Matrix?

Eine singuläre Matrix ist eine quadratische Matrix, deren Determinante gleich Null ist, sodass sie nicht invertierbar ist. 

Mathematisch ausgedrückt: Wenn det(A) = 0 für eine quadratische Matrix A ist, dann ist A singulär und hat keine inverse Matrix A-¹.

Die grundlegende Eigenschaft einer singulären Matrix ist, dass ihre Zeilen oder Spalten linear abhängig sind, d.h. mindestens eine Zeile (oder Spalte) kann als Linearkombination der anderen Zeilen (oder Spalten) ausgedrückt werden. Durch diese Abhängigkeit entsteht ein "Mangel" in der Matrix, der verhindert, dass sie eine eindeutige Umkehrung hat.

Eine weitere Möglichkeit, singuläre Matrizen zu verstehen, ist ihr Rang. Eine quadratische Matrix ist dann und nur dann singulär, wenn ihr Rang kleiner ist als die Anzahl der Zeilen (oder Spalten). Der Rang gibt die maximale Anzahl linear unabhängiger Zeilen oder Spalten an. Wenn dieser Wert die Matrixdimensionen unterschreitet, tritt Singularität auf.

Dieses Konzept ist wichtig, weil viele Algorithmen auf der Inversion von Matrizen beruhen, von der Lösung linearer Regressionsprobleme bis zur Implementierung bestimmter maschineller Lernverfahren. Wenn eine Matrix singulär ist, schlagen diese Operationen fehl und erfordern alternative Ansätze oder Vorverarbeitungsschritte, um die Situation zu bewältigen.

Eigenschaften und Bedingungen von singulären Matrizen

Wenn du die mathematischen Eigenschaften singulärer Matrizen verstehst, kannst du potenzielle Probleme erkennen, bevor sie zu Berechnungsproblemen in Data Science Workflows führen.

• Null-Determinante: Die Determinante einer singulären Matrix ist immer gleich Null, was direkt auf die Nicht-Invertierbarkeit hinweist. Diese Null-Determinante bedeutet, dass die Matrixtransformation nicht bijektiv ist, so dass mehrere Eingangsvektoren auf denselben Ausgang abgebildet werden können.
• Lineare Abhängigkeit: Singuläre Matrizen enthalten linear abhängige Zeilen oder Spalten, wobei mindestens eine Zeile als Linearkombination der anderen ausgedrückt werden kann. Durch diese Abhängigkeit entstehen redundante Informationen, die zu rechnerischen Herausforderungen führen.
• Rangmangel: Eine singuläre n×n-Matrix hat einen Rang kleiner als n und besitzt weniger linear unabhängige Zeilen oder Spalten als ihre Dimension. Diese Unzulänglichkeit erklärt, warum Systeme mit singulären Matrizen keine eindeutigen Lösungen haben.
• Null-Eigenwerte: Mindestens ein Eigenwert einer singulären Matrix ist genau null, was den Richtungen im Raum entspricht, die bei der Transformation vollständig kollabieren. Die Anzahl der Null-Eigenwerte entspricht der Nullität der Matrix.
• Nicht-trivialer Nullraum: Singuläre Matrizen haben Nicht-Null-Vektoren, die, wenn sie mit der Matrix multipliziert werden, den Null-Vektor ergeben. Die Dimension dieses Nullraums gibt an, wie viel Information bei der Transformation verloren geht.

Nachdem wir nun die grundlegenden Eigenschaften einer singulären Matrix verstanden haben, wollen wir sie mit nicht-singulären Matrizen vergleichen.

Singular vs. Nicht-singuläre Matrix

Nicht-singuläre Matrizen sind invertierbar und ermöglichen zuverlässige numerische Berechnungen, während singuläre Matrizen keine Inversen haben und eine spezielle Handhabung erfordern. Diese grundlegende Unterscheidung bestimmt die rechnerische Machbarkeit von Data Science-Anwendungen. 

Diese Unterschiede gelten für jede der grundlegenden Eigenschaften einer singulären Matrix, die wir bereits gesehen haben. Die folgende Tabelle fasst die Unterschiede zwischen singulären und nicht-singulären Matrizen zusammen:

Beispiele für singuläre Matrizen

Anhand von konkreten Beispielen wird deutlich, wie sich die Einzigartigkeit in der Praxis manifestiert, und es wird ein Gespür dafür entwickelt, wie man diese Matrizen erkennt.

Einfache 2×2 Singulärmatrix

Betrachte dieses einfache Beispiel, bei dem eine Zeile ein Vielfaches einer anderen ist:

Einfache 2×2 Singulärmatrix (Bild vom Autor)

Hier ist die zweite Reihe genau die Hälfte der ersten Reihe, wodurch eine lineare Abhängigkeit entsteht. Die Determinante ist (2×2) - (4×1) = 0, was die Singularität bestätigt.

Null Zeile oder Spalte

Jede Matrix, die eine Zeile oder Spalte mit lauter Nullen enthält, ist automatisch singulär:

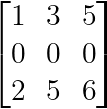
Null Zeile oder Spalte (Bild vom Autor)

Die Nullzeile macht es unmöglich, dass die Matrix unabhängig von den anderen Einträgen einen vollen Rang hat.

Identische Zeilen oder Spalten

Matrizen mit identischen Zeilen oder Spalten sind immer singulär:

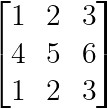
Identische Zeilen oder Spalten (Bild vom Autor)

Die erste und die dritte Zeile sind identisch, wodurch eine perfekte lineare Abhängigkeit entsteht.

Lineare Kombinationsabhängigkeit

Eine subtilere Singularität tritt auf, wenn eine Reihe gleich einer Kombination von anderen ist:

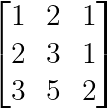
Lineare Kombinationsabhängigkeit (Bild vom Autor)

Hier ist die dritte Zeile gleich der Summe der ersten beiden Zeilen: [3,5,2] = [1,2,1] + [2,3,1].

Jedes dieser Beispiele zeigt, wie scheinbar unterschiedliche Matrizen die grundlegende Eigenschaft der linearen Abhängigkeit teilen können, die die Singularität definiert.

Warum gibt es singuläre Matrizen in der Datenwissenschaft?

Singuläre Matrizen tauchen häufig in datenwissenschaftlichen Anwendungen auf, weil es sich um reale Daten und gängige analytische Arbeitsabläufe handelt.

Multikollinearität in Merkmalssätzen

Die häufigste Ursache für singuläre Matrizen in der Datenwissenschaft ist Multikollinearität, wenn mehrere Merkmale in einem Datensatz perfekt oder nahezu perfekt korreliert sind. Dadurch entsteht eine lineare Abhängigkeit zwischen den Spalten in der Entwurfsmatrix, was zu Singularität bei Matrixoperationen führt.

Betrachte einen Einzelhandelsdatensatz mit Merkmalen für total_sales, q1_sales, q2_sales, q3_sales und q4_sales. Wenn die Summe der vierteljährlichen Umsatzwerte immer genau dem Gesamtumsatz entspricht, dann:

total_sales = q1_sales + q2_sales + q3_sales + q4_sales

Wenn diese Beziehung über alle Beobachtungen hinweg perfekt ist, wird die resultierende Designmatrix singulär. Jeder lineare Regressionsalgorithmus, der versucht, diese Matrix zu invertieren, wird scheitern, weil eine Spalte perfekt aus den anderen vorhergesagt werden kann.

Ähnliche Szenarien treten bei abgeleiteten Merkmalen wie:

• Temperatur in Celsius und Fahrenheit
• Alter und Geburtsjahr (bei einem festen Bezugsjahr)
• Verhältnisse, bei denen der Zähler und der Nenner auch Merkmale sind
• Dummy-Variablen, deren Summe eine Konstante ergibt (die Dummy-Variablenfalle)

Unzureichende Daten in Bezug auf die Merkmale

Bei hochdimensionalen Datensätzen mit weniger Beobachtungen als Merkmalen entstehen natürlich singuläre Matrizen. Wenn du n Stichproben, aber p Merkmale hast, bei denen p > n ist, hat die resultierende n×n Kovarianzmatrix oder Grammatrix höchstens den Rang n, was sie singulär macht, wenn du eine p×p invertierbare Matrix brauchst.

Dieser "Fluch der Dimensionalität" wirkt sich häufig aus:

• Genomische Daten mit Tausenden von Genen, aber Hunderten von Proben
• Textanalyse mit großen Vokabularen, aber begrenzten Dokumenten
• Bildverarbeitung mit hochauflösenden Merkmalen, aber kleinen Trainingsmengen
• Finanzmodellierung mit vielen Wirtschaftsindikatoren, aber kurzen Zeitreihen

Vorverarbeitung der Daten 

Gängige Schritte der Datenvorverarbeitung können unbeabsichtigt zu Singularitäten führen:

• Zentrierende Transformationen: Die Zentrierung jedes Merkmals (Subtraktion des Mittelwerts) verursacht für sich genommen keine Singularität, kann aber bei Vorhandensein anderer linearer Abhängigkeiten diese erhalten oder betonen. In Fällen, in denen die Merkmale bereits annähernd abhängig sind, kann die Zentrierung sie bei begrenzter Genauigkeit näher an die exakte Abhängigkeit heranführen.
• Skalierung und Normalisierung: Bestimmte Skalierungsoperationen können subtile lineare Beziehungen noch deutlicher machen, indem sie fast abhängige Merkmale aufgrund der Grenzen der Gleitkommagenauigkeit in eine perfekte Abhängigkeit bringen.
• Feature Engineering: Das Erstellen von polynomialen Merkmalen, Interaktionstermen oder Basiserweiterungen kann unerwartete lineare Beziehungen einführen. Wenn du zum Beispiel die Merkmale x, ^x² und ^2x²- x erstellst, ist das dritte Merkmal(^2x²- x) durch die ersten beiden perfekt bestimmt.

Das Verständnis dieser häufigen Ursachen für Singularität ermöglicht es Datenwissenschaftlern, frühzeitig Präventivmaßnahmen in ihre Arbeitsabläufe einzubauen, wie z.B. die Überprüfung auf Multikollinearität während der explorativen Datenanalyse oder den proaktiven Einsatz von Regularisierungstechniken.

Da wir nun wissen, warum singuläre Matrizen in der Datenwissenschaft vorkommen, wollen wir uns mit praktischen Methoden beschäftigen, um sie zu erkennen, bevor sie zu Rechenfehlern führen.

Wie man singuläre Matrizen erkennt

Der einfachste Weg, eine singuläre Matrix zu erkennen, ist die Überprüfung ihrer Determinante. Wenn die Determinante einer quadratischen Matrix null ist, ist die Matrix singulär und nicht invertierbar. Diese Methode ist einfach, mathematisch fundiert und in der Praxis weit verbreitet.

Wir wollen verstehen, wie man diese Prüfung mit Python durchführt:

import numpy as np

# Example 2x2 matrix
A = np.array([[2, 4],
             [1, 2]])

# Calculate the determinant
det_A = np.linalg.det(A)

print(f"Determinant of A: {det_A}")

# Check if matrix is singular
if np.isclose(det_A, 0):
   print("Matrix A is singular.")
else:
   print("Matrix A is non-singular.")

Im obigen Beispiel definieren wir eine 2×2-Matrix A und verwenden np.linalg.det(), um ihre Determinante zu berechnen. Da die Fließkommaarithmetik kleine numerische Fehler verursachen kann, verwenden wir np.isclose(), um zu prüfen, ob die Determinante tatsächlich Null ist. Wenn dies der Fall ist, schließen wir daraus, dass die Matrix singulär ist. 

Wir sehen unten die Ausgabe, die die Singularität bestätigt:

Ausgabe der singulären Matrix. (Bild vom Autor)

Diese Methode ist sowohl intuitiv als auch praktisch, was sie zu einem zuverlässigen ersten Schritt bei der Diagnose von Problemen im Zusammenhang mit der Invertierbarkeit von Matrizen in Data Science Workflows macht.

Wie man mit singulären Matrizen in der Praxis umgeht

Wenn du in datenwissenschaftlichen Arbeitsabläufen mit singulären Matrizen konfrontiert wirst, gibt es mehrere Strategien, um die rechnerischen Herausforderungen zu bewältigen und gleichzeitig die analytische Integrität zu bewahren.

Regularisierungstechniken

Die Hinzufügung kleiner Werte zur Diagonalen (Ridge-Regularisierung) ist derhäufigste Ansatz für den Umgang mit nahezu singulären Matrizen bei Regressionsproblemen. Mit dieser Technik werden singuläre Matrizen in invertierbare Matrizen umgewandelt, wobei die numerische Stabilität erhalten bleibt:

# Ridge regularization approach
lambda_reg = 1e-6
A_regularized = A + lambda_reg * np.eye(A.shape[0])

Berechnung der Pseudoinverse

Die Moore-Penrose-Pseudoinverse ist eine verallgemeinerte Umkehrung für singuläre Matrizen und bietet die "beste" Lösung im Sinne der kleinsten Quadrate:

# Using pseudoinverse for singular matrices
A_pinv = np.linalg.pinv(A)
x = A_pinv @ b 

Dimensionalitätsreduktion

Durch das Entfernen linear abhängiger Merkmale wird die Singularität an ihrerQuelle beseitigt. Mitder Hauptkomponentenanalyse oderMerkmalsauswahlverfahren können redundante Dimensionen identifiziert und entfernt werden:

# PCA-based dimensionality reduction
from sklearn.decomposition import PCA
pca = PCA(n_components=0.95) 
X_reduced = pca.fit_transform(X)

Alternative Algorithmen

Einige Algorithmen sind speziell für singuläre Matrizen entwickelt worden. Die QR-Zerlegung mit Pivotierung kann lineare Systeme auch dann lösen, wenn die Koeffizientenmatrix singulär ist. Sie liefert Lösungen, wenn sie existieren, und identifiziert Unstimmigkeiten, wenn sie nicht existieren.

Diese Strategien stellen sicher, dass singuläre Matrizen Data-Science-Projekte nicht zum Scheitern bringen und gleichzeitig die mathematische Strenge und Interpretierbarkeit der Ergebnisse erhalten bleibt.

Fazit

In diesem Artikel haben wir gelernt, dass singuläre Matrizen quadratische Matrizen mit Null-Determinanten sind, die aufgrund von linearen Abhängigkeiten zwischen den Zeilen oder Spalten nicht invertiert werden können. Wir haben uns angesehen, warum sie in der Datenwissenschaft häufig auftreten, von Multikollinearität und hochdimensionalen Daten bis hin zu Problemen, die bei der Vorverarbeitung auftreten. 

In diesem Artikel haben wir uns auch angesehen, wie man singuläre Matrizen mit grundlegenden Techniken wie Determinantenprüfung, Regularisierung, Pseudoinversen und Dimensionalitätsreduktion erkennt und behandelt. (Wenn du selbst weiterforschen möchtest, können Werkzeuge wie die Zustandszahlanalyse oder die Singulärwertzerlegung noch mehr Einblicke in das Matrixverhalten und die numerische Stabilität geben).

Um dein Verständnis der linearen Algebra und ihrer wichtigen Rolle in Data Science-Anwendungen zu vertiefen, melde dich für unseren Kurs Lineare Algebra für Data Science an, in dem du diese grundlegenden Konzepte und ihre Umsetzung in realen Szenarien lernst.