Poisson-Verteilung: Ein umfassender Leitfaden

In der Statistik und Datenwissenschaft ist die Poisson-Verteilung ein wichtiges Instrument zur Modellierung diskreter Ereignisse, die innerhalb eines festen Intervalls auftreten. Diese nach dem französischen Mathematiker Siméon Denis Poisson benannte Wahrscheinlichkeitsverteilung hilft bei der Analyse und Vorhersage seltener Ereignisse und ist daher für Datenexperten in verschiedenen Bereichen sehr nützlich.

Wenn du neu in der Statistik bist, bietet dir unser Kurs "Einführung in die Statistik" eine solide Grundlage, um diese Konzepte zu begreifen. Für diejenigen, die bereit sind, die Wahrscheinlichkeitstheorie wirklich zu lernen, bietet der Kurs Grundlagen der Wahrscheinlichkeit in Python eine umfassende Erkundung probabilistischer Konzepte, einschließlich der Poisson-Verteilung. 

Was ist eine Poisson-Verteilung?

Die Poisson-Verteilung ist eine diskrete Wahrscheinlichkeitsverteilung, die die Wahrscheinlichkeit ausdrückt, dass eine bestimmte Anzahl von Ereignissen in einem festen Zeit- oder Raumintervall eintritt. Dabei wird davon ausgegangen, dass diese Ereignisse mit einer bekannten durchschnittlichen Rate und unabhängig von der Zeit seit dem letzten Ereignis eintreten. Um die Poisson-Verteilung zu verstehen, ist es zunächst hilfreich, den Unterschied zwischen diskreten und kontinuierlichen Verteilungen zu kennen.

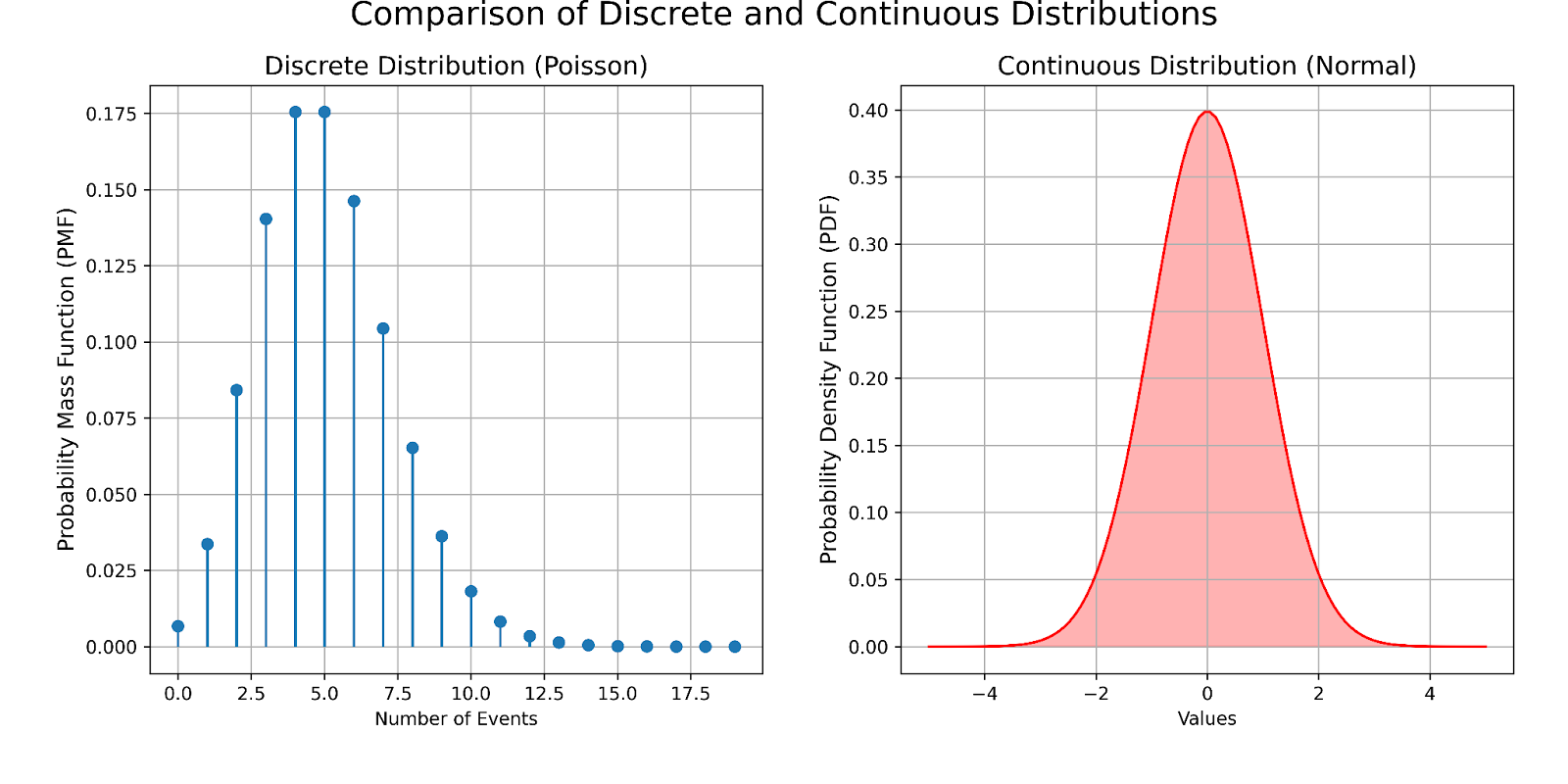
Poisson-Verteilung vs. eine kontinuierliche Verteilung. Bild vom Autor

Diskrete Verteilungen

• Natur: Diskrete Verteilungen beschreiben Phänomene, bei denen die Ergebnisse in ganzen Zahlen gezählt werden können. Sie sind durch Wahrscheinlichkeitsmassenfunktionen (PMF) gekennzeichnet, die jedem möglichen diskreten Ergebnis eine Wahrscheinlichkeit zuweisen.
• Visualisierung: Im linken Feld ist die Poisson-Verteilung dargestellt, bei der jeder Punkt die Wahrscheinlichkeit darstellt, dass eine bestimmte Anzahl von Ereignissen innerhalb eines festen Intervalls eintritt. Diese Verteilung ist ideal für die Modellierung von Zähldaten, z. B. die Anzahl der pro Stunde eingegangenen E-Mails. Dir fällt vielleicht auch auf, dass es keine negativen Werte in der Poisson-Verteilungstafel gibt. Das liegt daran, dass Poisson-Verteilungen per Definition keine negativen Werte haben können.

Einige Beispiele für diskrete Wahrscheinlichkeitsverteilungen sind die Bernoulli- und die Binomial-Verteilung. 

Kontinuierliche Verteilungen

• Natur: Kontinuierliche Verteilungen werden für Daten verwendet, die jeden Wert innerhalb eines Bereichs annehmen können, einschließlich Dezimalzahlen. Sie verwenden Wahrscheinlichkeitsdichtefunktionen (PDF), um die Wahrscheinlichkeiten von Ergebnissen innerhalb eines bestimmten Bereichs zu beschreiben.
• Visualisierung: Das rechte Feld veranschaulicht die Normalverteilung. Die glatte Kurve zeigt die Dichte der Werte um den Mittelwert herum an, und die Fläche unter der Kurve zwischen zwei beliebigen Punkten gibt die Wahrscheinlichkeit an, in diesen Bereich zu fallen. Diese Art der Verteilung ist nützlich, um Größen wie Temperatur oder Gewicht zu messen.

Die Normal- oder Gaußverteilung ist das beste Beispiel für eine kontinuierliche Verteilung.

Eigenschaften von Poisson-Verteilungen

Schauen wir uns einige der wichtigen Merkmale der Poisson-Verteilung an.

Ereignisse in einem festen Intervall

Eine wichtige Eigenschaft der Poisson-Verteilung ist ihre Fähigkeit, Ereignisse in einem festen Intervall zu modellieren. Dieses Intervall kann zeitlich (z. B. die Anzahl der ankommenden Kunden pro Stunde) oder räumlich (z. B. die Anzahl der Fehler pro Quadratmeter Stoff) sein. Das Modell geht davon aus:

1. Ereignisse treten unabhängig voneinander auf.
2. Die durchschnittliche Häufigkeit des Auftretens (λ) bleibt über das Intervall hinweg konstant.
3. Zwei Ereignisse können nicht genau zum gleichen Zeitpunkt stattfinden.

Mittelwert und Varianz

Eine der markantesten Eigenschaften der Poisson-Verteilung ist, dass ihr Mittelwert (Erwartungswert) gleich ihrer Varianz ist. Beide werden durch den Parameter λ (lambda) dargestellt, der die durchschnittliche Anzahl der Ereignisse im Intervall angibt. Diese Eigenschaft ist einzigartig und hilft dabei, zu erkennen, ob ein Datensatz einer Poisson-Verteilung folgt. Mathematisch lässt sich dies durch die folgende Gleichung darstellen: 

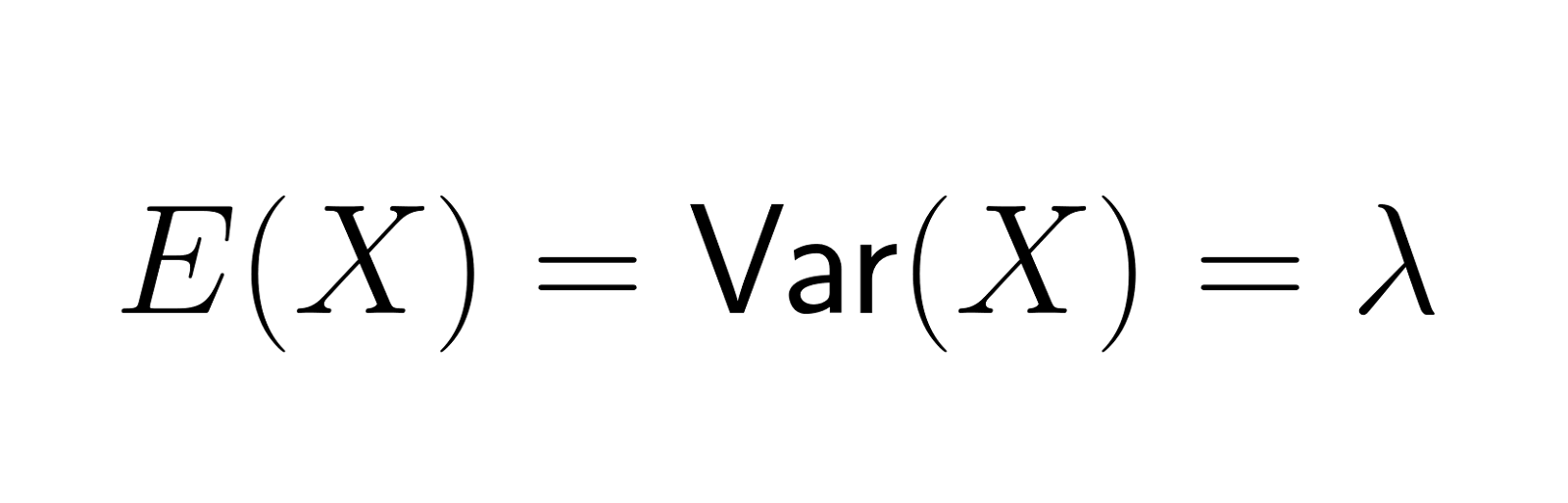
Diese Gleichheit bedeutet, dass mit der erwarteten Anzahl von Ereignissen auch die Variabilität der tatsächlichen Anzahl von Ereignissen zunimmt.

Schrägheit und Form

Die Form der Poisson-Verteilung variiert je nach dem Wert von λ. Diese visuelle Illustration zeigt, wie λ die Schiefe und Symmetrie der Verteilung beeinflusst: 

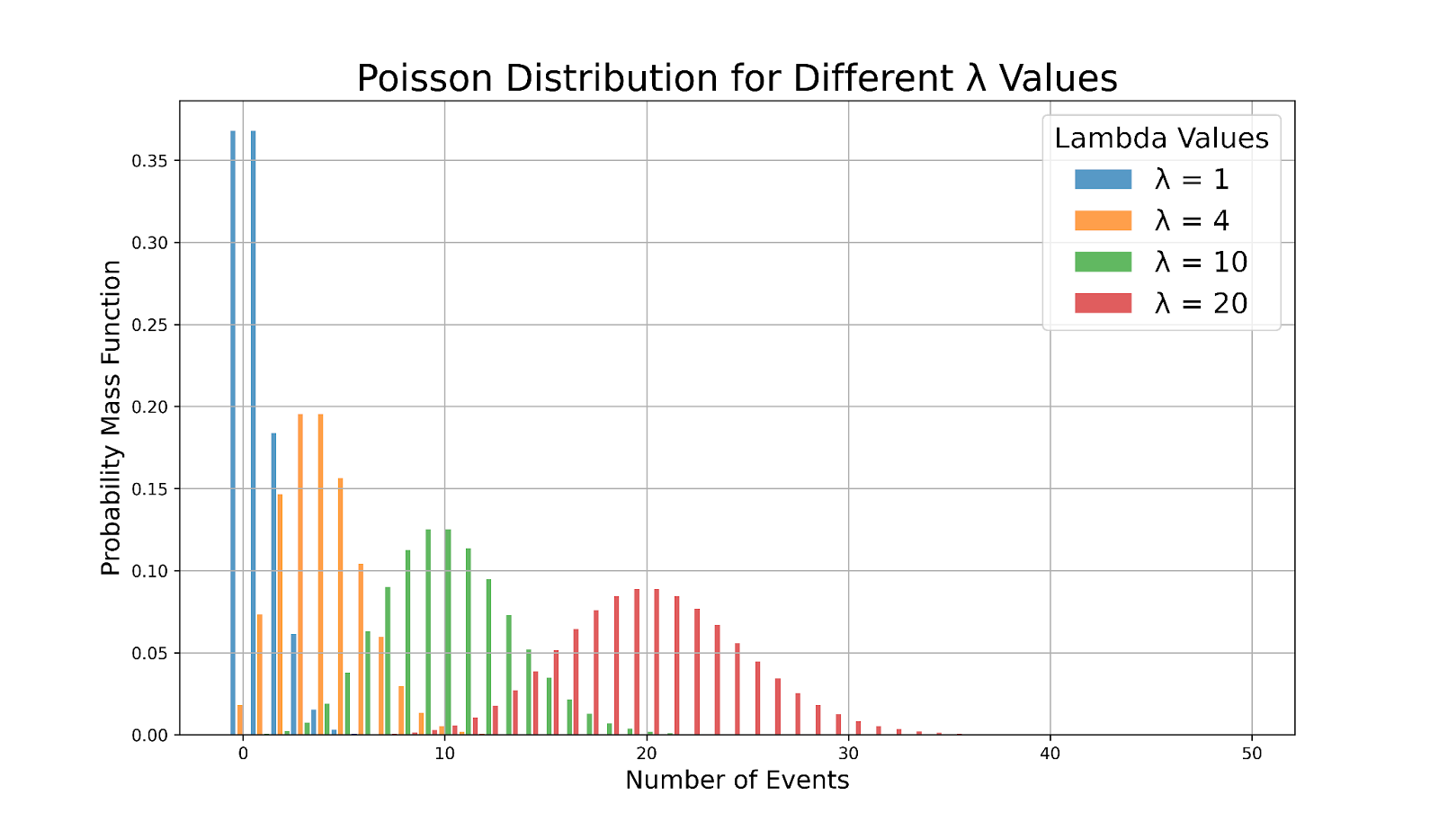
Poisson-Verteilungen mit unterschiedlichen Lambda-Werten. Bild vom Autor

• Für kleine λ-Werte (λ < 10) ist die Verteilung merklich rechtsschief. Das bedeutet, dass es mehr Vorkommnisse mit weniger Ereignissen und weniger Vorkommnisse mit einer größeren Anzahl von Ereignissen gibt.
• Mit zunehmendem λ (λ > 10) wird die Verteilung symmetrischer und beginnt, einer Normalverteilung zu ähneln. Diese Symmetrie zeigt an, dass die Daten gleichmäßiger um den Mittelwert verteilt sind.

Diese sich verändernde Form hat Auswirkungen darauf, wie wir Wahrscheinlichkeiten interpretieren und Schlüsse aus Poisson-Verteilungsdaten ziehen. Eine symmetrische Verteilung vereinfacht zum Beispiel viele Arten von Analysen, wie Hypothesentests und Konfidenzintervallschätzungen, weil die Verteilung der Daten besser vorhersehbar und ausgeglichen ist.

Formel für die Poisson-Verteilung

Sieh dir die Formel der Poisson-Verteilung an. 

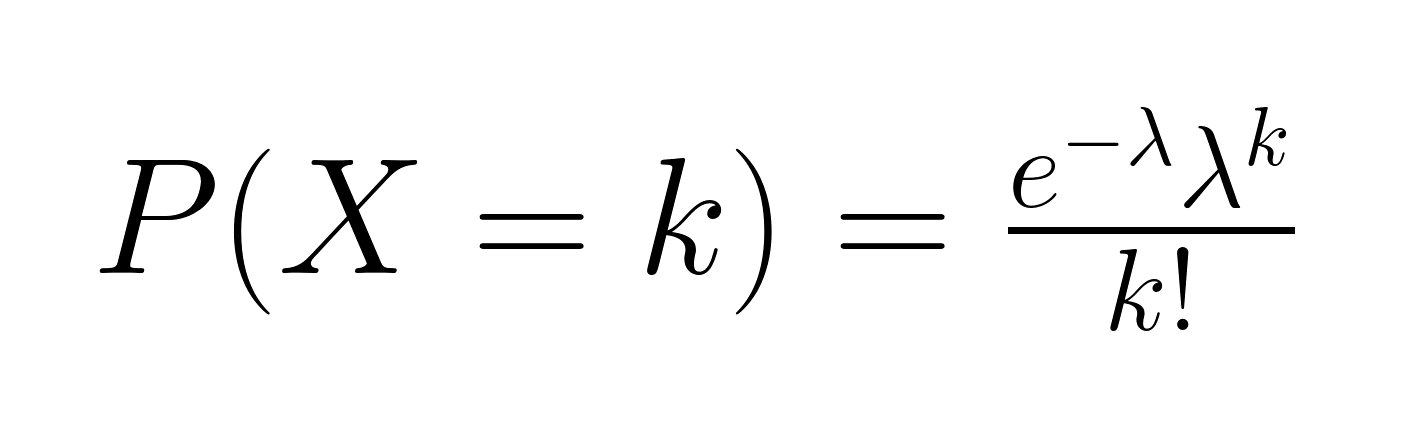
• Die linke Seite (LHS) der Poisson-Verteilungsformel, P(X = k), stellt die Wahrscheinlichkeit dar, dass genau k Ereignisse innerhalb eines festen Intervalls eintreten. X ist die Anzahl der Ereignisse und k ist die Zahl, an der wir interessiert sind. Mit anderen Worten: Die linke Seite sagt uns, welche Wahrscheinlichkeit wir berechnen.

• Der Zähler auf der rechten Seite (RHS),^e-λλk, besteht aus zwei Teilen. ^λk gibt an, wie wahrscheinlich es ist, dass k Ereignisse eintreten, basierend auf der durchschnittlichen Rate λ. Die ^e-λ Term trägt der Zufälligkeit der Ereignisse Rechnung und sorgt dafür, dass die Wahrscheinlichkeit abnimmt, wenn die Anzahl der Ereignisse von der erwarteten Rate abweicht.

• Der Nenner auf der rechten Seite (RHS), k!, passt an, auf wie viele Arten die Ereignissevon x auftreten können. Die faktorielle Notation berechnet die Anzahl der möglichen Anordnungen und stellt sicher, dass die Wahrscheinlichkeit die Tatsache widerspiegelt, dass die Reihenfolge der Ereignisse keine Rolle spielt.

Wenn du wirklich sicher im Umgang mit Python für maschinelles Lernen werden willst, dann starte unseren Karrierepfad Machine Learning Scientist with Python, in dem du fortgeschrittene Techniken mit echten Datensätzen üben kannst.