KL-Divergenz erklärt: Intuition, Formel und Beispiele

Beim maschinellen Lernen ist es super wichtig, wie genau unsere Modelle die Ergebnisse in der echten Welt vorhersagen. Egal, ob du ein Wettervorhersagemodell erstellst oder ein Empfehlungssystem optimierst, du musst irgendwie messen können, wie gut deine Vorhersagen mit der Realität übereinstimmen. Ein super Ansatz dafür ist die KL-Divergenz.

In diesem Artikel werde ich erklären, was KL-Divergenz ist, warum sie wichtig ist, wie man sie intuitiv versteht, welche mathematischen Grundlagen dahinterstecken und praktische Beispiele zeigen, wie man sie anwenden kann.

Wenn du dich mit Machine Learning-Konzepten beschäftigst, empfehle ich dir den Lernpfad „Grundlagen des maschinellen Lernens in Python“.

Was ist KL-Divergenz?

KL-Divergenz (Kullback-Leibler-Divergenz) ist ein statistisches Maß , mit dem man sieht, wie sehr eine Wahrscheinlichkeitsverteilung von einer anderen Referenzverteilung abweicht.

Nehmen wir mal an, wir bauen zusammen ein Modell, um das Wetter für morgen vorherzusagen. Im Hintergrund macht unser Modell Wetten – es gibt Wahrscheinlichkeiten für mögliche Ergebnisse. Aber hier ist eine wichtige Frage, die man sich stellen sollte:

Wie misst du, wie weit diese Wetten von der Realität entfernt sind? 

Wir brauchen eine Möglichkeit, diesen Unterschied zu messen, und da kommt die KL-Divergenz ins Spiel. Es ist ein mathematisches Tool, das den Unterschied zwischen dem, was unser Modell denkt, und dem, was wirklich stimmt, misst.

Wie ich schon gesagt habe, ist die KL-Divergenz (oder, wenn man es ganz genau nimmt, die Kullback-Leibler-Divergenz) das A und O in der modernen Datenwissenschaft, im maschinellen Lernen und in der KI. Es sagt uns in Bits oder Nats (mehr dazu später), wie viel „zusätzliche Überraschung“ oder „Informationsverlust“ wir haben, wenn wir eine Wahrscheinlichkeitsverteilung (z. B. die Vorhersagen unseres Modells, Q) verwenden, um eine andere (die reale Wahrheit, P) zu schätzen. 

Es ist sozusagen der Richter bei der Modellbewertung, der Regulierung in neuronalen Netzwerken, bei Bayes'schen Aktualisierungen und sogar dabei, wie wir Daten komprimieren oder Nachrichten effizient übertragen.

Um wirklich zu verstehen, wie wichtig die KL-Divergenz ist, stell dir das so vor: Jedes Mal, wenn unser Modell eine Vorhersage macht, ist das eigentlich nur ein Glücksspiel mit der Zukunft. KL-Divergence ist die Scorecard, die berechnet, wie teuer diese Wetten sind. Das gleiche Prinzip gilt für viele Themen im Bereich des maschinellen Lernens, egal ob wir einen Chatbot trainieren, eine Krankheit diagnostizieren oder eine Werbekampagne optimieren.

Mathematisch wird die KL-Divergenz so definiert:

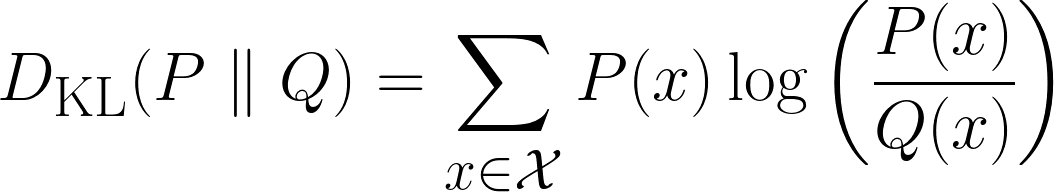
Oben ist die Formel für diskrete Fälle und unten die für kontinuierliche Fälle.

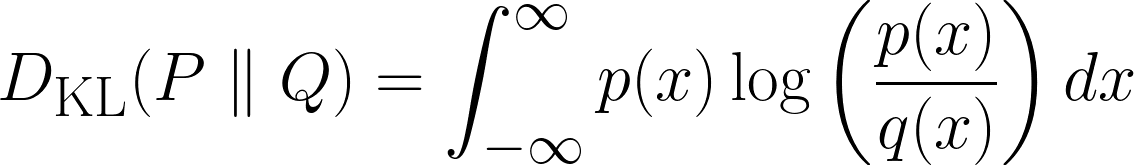
Die Idee hinter der KL-Divergenz

In diesem Abschnitt werden wir die KL-Divergenz intuitiv herleiten.  Lass uns mit ein paar Fragen anfangen.

Überraschung verstehen

„Wenn du eine Münze werfen würdest und ich das Ergebnis genau erraten würde, wärst du überrascht?“ Ich denke, du wärst ein bisschen überrascht, aber nicht total schockiert. Kommen wir jetzt zum zweiten Szenario.

„Wenn du würfelst und ich das Ergebnis genau errate, wärst du dann mehr überrascht als im vorherigen Szenario?“ Ich nehme an, du würdest ja sagen, da es für mich unwahrscheinlicher ist, das richtige Ergebnis zu erraten.

Jetzt noch ein letztes Szenario:

„Wenn ich die Lottozahlen richtig erraten hätte, wärst du dann jetzt überraschter als im vorherigen Szenario?“ Ich nehme an, du würdest ja sagen und total schockiert sein. Aber warum eigentlich?

Das liegt daran, dass die Wahrscheinlichkeit, dass ich das richtige Ergebnis erraten konnte, im Laufe der Szenarien immer geringer wurde und deine Überraschung über das Ergebnis daher immer größer wurde. Wir haben also gerade eine Beziehung entdeckt:

Die Wahrscheinlichkeit, dass etwas passiert, hängt umgekehrt davon ab, wie überraschend es ist. 

Um es klar zu sagen: Je unwahrscheinlicher etwas passiert, desto größer ist die Überraschung und umgekehrt. 

Hier können wir aber noch was Interessantes feststellen. Wenn wir noch mal zu den Würfeln zurückkommen und uns vorstellen, dass du dreimal denselben Würfel wirfst und ich jedes Mal richtig rate, wie viel überraschter wärst du dann, als wenn es nur einen Würfel gäbe und ich jedes Mal richtig rate? 

Also, deine Überraschung wäre nicht nur ein bisschen größer als bei einer einzigen richtigen Antwort, sondern echt viel größer, am besten dreimal so groß. Warum? Denn jede neue richtige Vermutung verstärkt deine Zweifel. Es geht nicht nur darum, eine feste Menge an Überraschung hinzuzufügen, sondern darum, das Gefühl der Unglaubwürdigkeit der Situation zu verstärken.

Wenn wir also versuchen, Überraschung mathematisch zu definieren, möchten wir, dass sie folgende Eigenschaften hat:

1. Additive Eigenschaft: Wenn zwei unabhängige Ereignisse passieren, sollte die Überraschung, die sie zusammen auslösen, der Summe ihrer einzelnen Überraschungen entsprechen.
1. Beispiel: 1 Würfelwurf richtig erraten → Überraschung = S. 2 Würfelwürfe richtig erraten → Überraschung = S + S = 2S.
2. Umgekehrte Beziehung zur Wahrscheinlichkeits. Je unwahrscheinlicher ein Ereignis ist, desto überraschender ist es.
1. Beispiel: Ein Münzwurf (50 %) ist weniger überraschend als ein Lottogewinn (0,000001 %).
3. Keine Überraschung bei bestimmten Ereignissen. Wenn etwas immer passiert (Wahrscheinlichkeit = 1), sollte die Überraschung gleich Null sein.
1. Beispiel: „Heute ist die Sonne aufgegangen.“ → Das ist ja keine Überraschung.
4. Kontinuierliche Skalierungs. Eine kleine Änderung der Wahrscheinlichkeit sollte zu einer sanften, logischen Änderung der Überraschung führen (keine plötzlichen Sprünge).

Auf den ersten Blick könnte man denken, dass die mathematische Definition ziemlich kompliziert ist, weil es so viele Anforderungen gibt. Aber das ist es nicht!

Alle oben genannten Anforderungen können durch Manipulation der Logarithmusfunktion gelöst werden. Die eigenständige Logarithmusfunktion (oft werden log(x) und ln(x) gleich verwendet) sieht so aus:

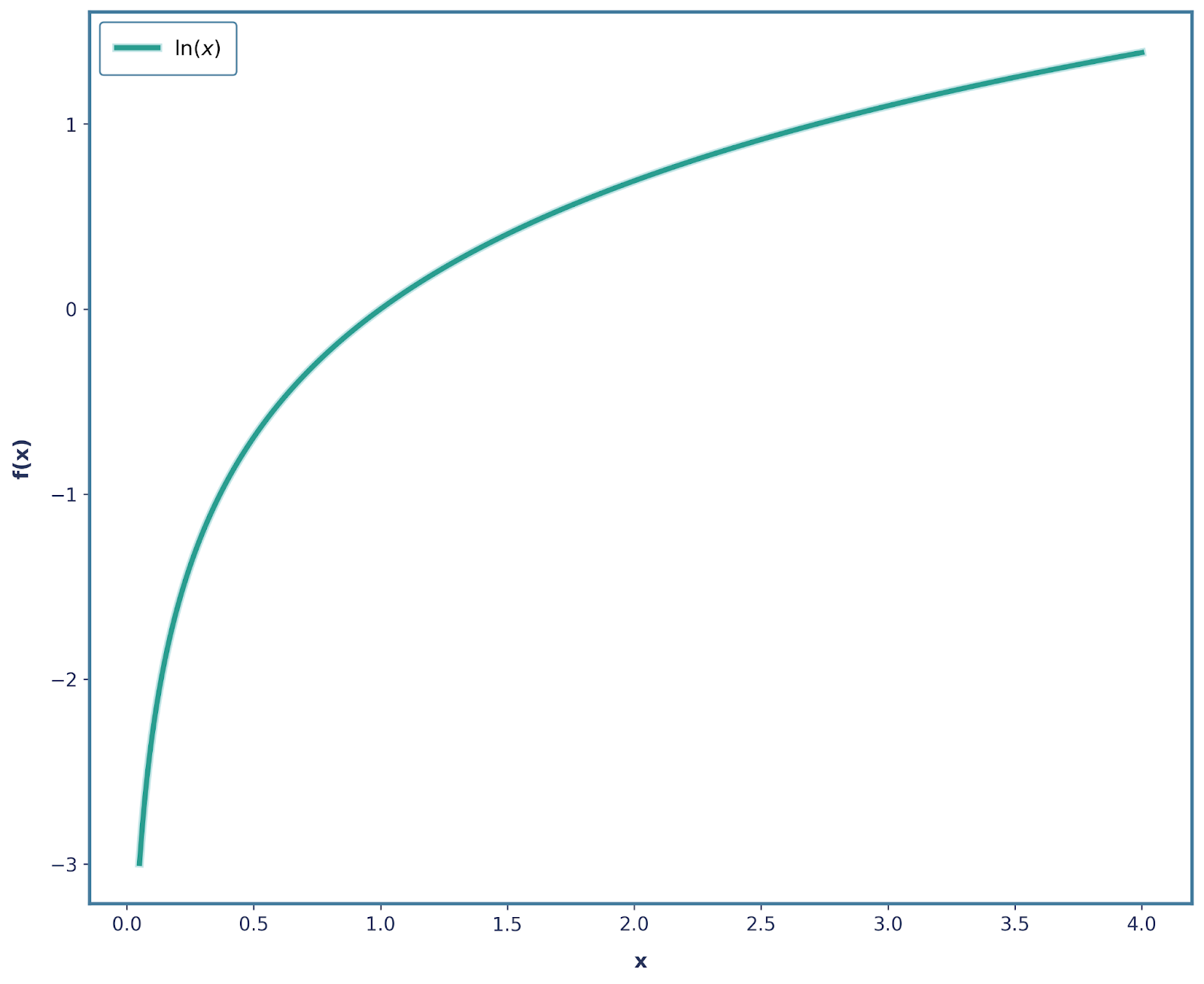
Wir haben schon ziemlich viele unserer Anforderungen erfüllt. Schauen wir uns erst mal dieadditive Eigenschaft „ “ an:. Weißt du noch, wie wir gesagt haben, dass, wenn zwei unabhängige Ereignisse passieren, die Gesamtüberraschung die Summe ihrer einzelnen Überraschungen sein sollte? Genau das macht die Log-Funktion!

So geht's:

Die Wahrscheinlichkeit, mit einem fairen Würfel eine 6 zu würfeln, ist ⅙. Definieren wir die Überraschung des Ereignisses wie folgt:

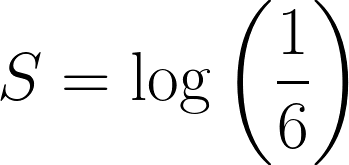
Nimm jetzt mal an, du würfelst dreimal hintereinandereine 6 . Die Wahrscheinlichkeit dafür wäre dann: ⅙ * ⅙ * ⅙ = 1/216. 

Was die Überraschung angeht, wäre es:

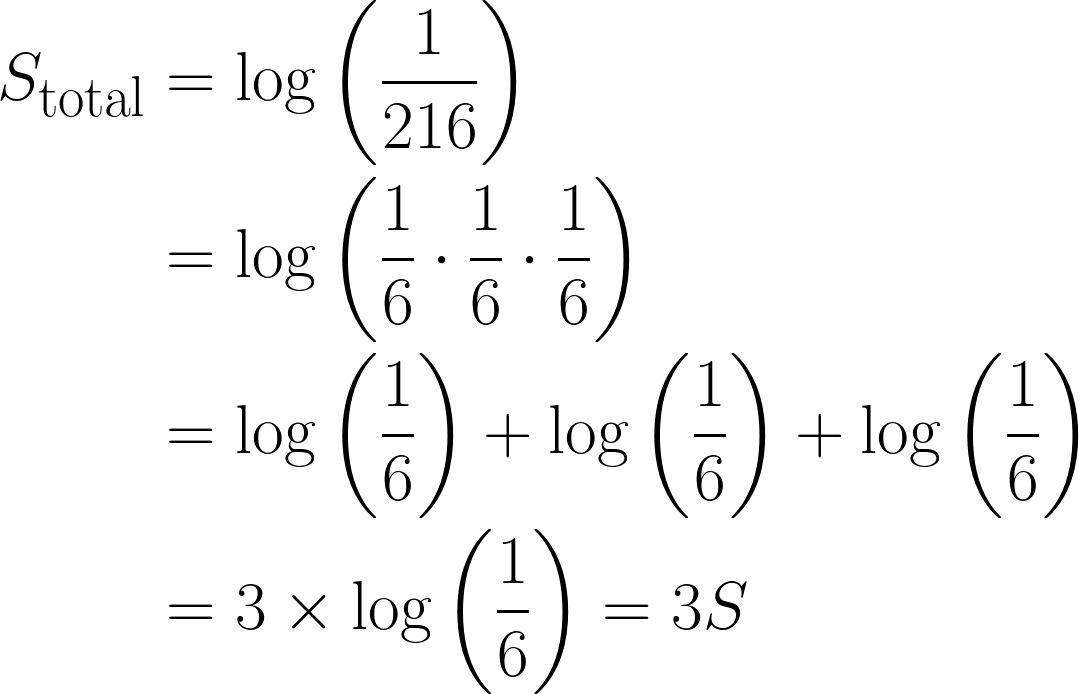
Das ist echt wichtig, weil die Überraschung durch den Logarithmus, den wir benutzt haben, um das Dritte gestiegen ist. Außerdem passt das auch zu Eigenschaft 3, wo log(1) = 0 ist, weil ein Ereignis, das ganz sicher passiert, keine Überraschung ist. 

Außerdem ist Eigenschaft 4 erfüllt, weil log(x) eine durchgehend monotone Funktion ist! Allerdings ist Eigenschaft 2 nicht erfüllt, da unsere Überraschung abnimmt, wenn die Wahrscheinlichkeit sinkt (da sie negativer wird). 

Wir können das ganz einfach lösen, indem wir ein Minuszeichen setzen! Also ist unsere Funktion jetzt -log(x), die so aussieht. 

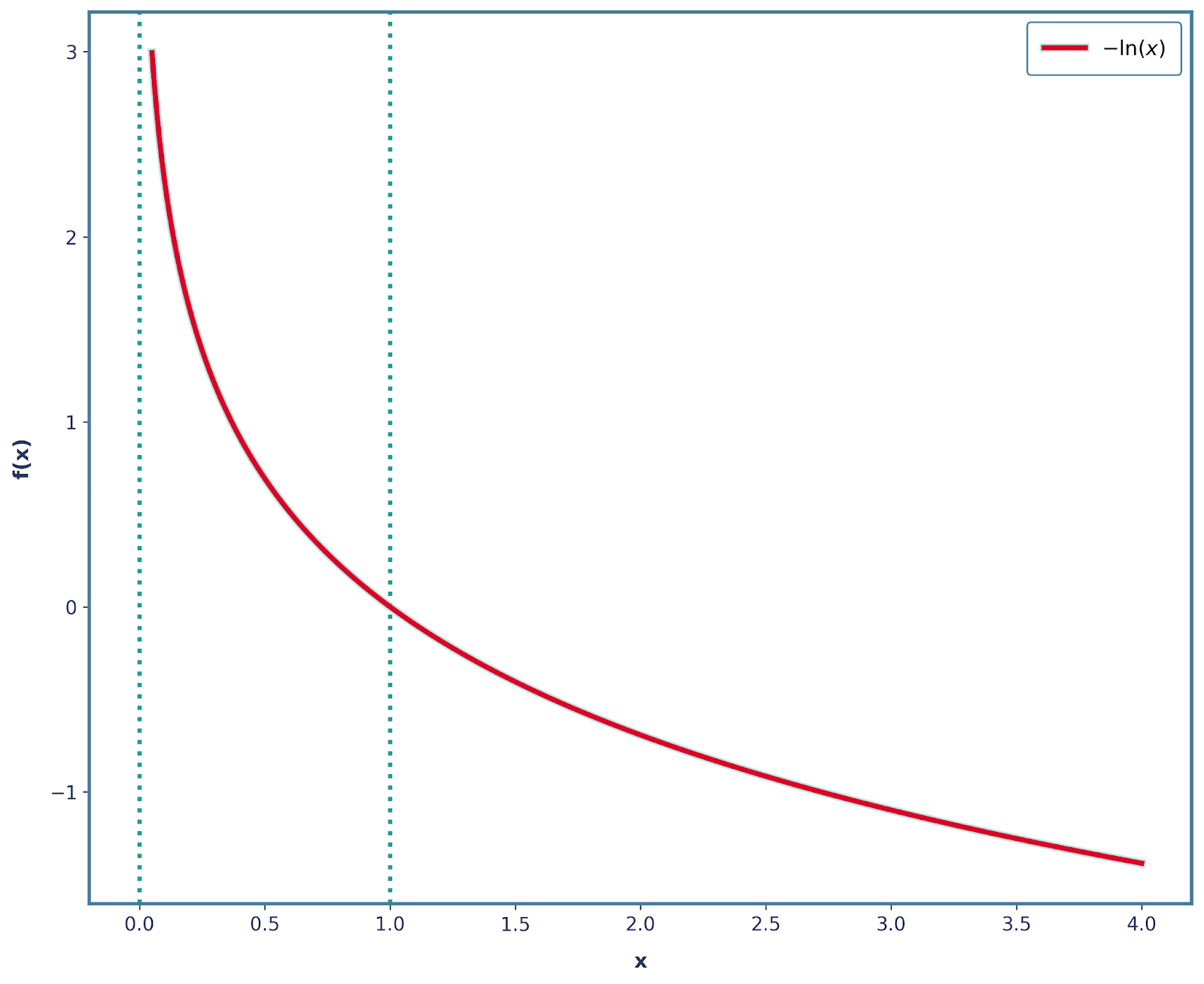
Es ist auch wichtig zu erwähnen, dass alle anderen 3 Eigenschaften mit dieser Änderung weiterhin erfüllt sind. Deshalb können wir Überraschung mathematisch so definieren: 

Entropie

Beim maschinellem Lerneninteressiert uns nicht nur die Überraschung eines einzelnen Ereignisses, sondern die durchschnittliche Überraschung aller möglichen Ereignisse. Das nennt man die erwartete Überraschung. Genauer gesagt wollen wir wissen, wie überraschend die Verteilung sein wird.

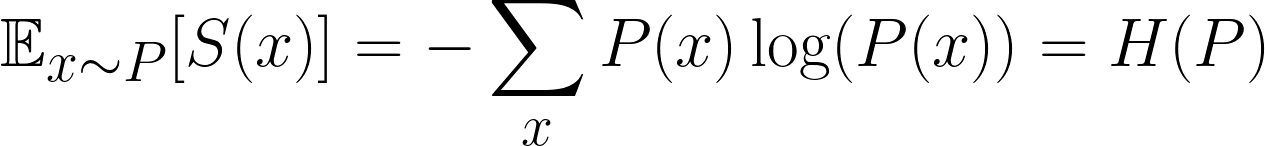
Das ist eine bekannte Formel und beschreibt die erwartete Überraschung, besser bekannt als Entropie. Irgendwie verwirrend ist, dass wir oft P und Q für unsere Verteilungen benutzen, also verwechsel das nicht mit p, das Wahrscheinlichkeit bedeutet!

Einfach gesagt, multiplizieren wir nur die Wahrscheinlichkeit jedes Ergebnisses mit der Wahrscheinlichkeit, dass das Ergebnis eintritt. Wahrscheinlichkeit jedes Ergebnisses mit ihrer Überraschungund dann über alle möglichen Ergebnisse addiert.

Ab jetzt sagen wir, dass P(x) unsere wahre zugrunde liegende Verteilung ist und Q(x)die Verteilung , die wir an P(x)annähern wollen (also istQ(X)die „falsche” Verteilung). Das ist beim maschinellen Lernen echt üblich – unsere Modelle versuchen ständig, die reale Welt zu schätzen.

Jetzt kommt die große Frage:

Was passiert, wenn wir unsere Überraschung mit der falschen Verteilung berechnen?

Wir können immer noch die Überraschung berechnen, aber statt P(x) messen wir sie jetzt in Bezug auf Q(x). Das gibt uns neue Hoffnung:

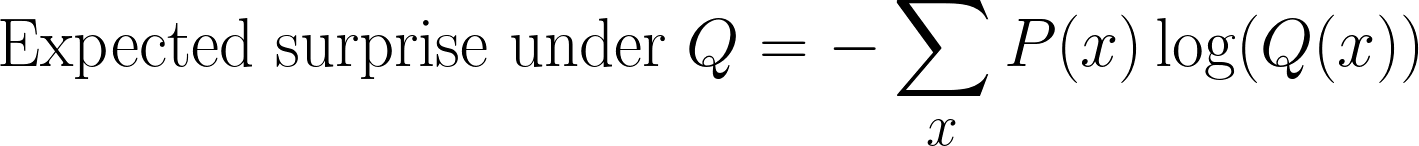
Das ist oft ein verwirrender Schritt, wenn man die KL-Divergenz berechnet. Wir nehmen immer noch Proben nach„ “ P(x) (weil das die wahre Verteilung ist), aber wir messen die Überraschung mit Q(x)(der Annahme unseres Modells).

Diese Größe wird manchmal als Kreuzentropie zwischen P(x)und Q(x).

KL-Divergence Formula

Bis jetzt haben wir zwei Größen definiert:

1. Entropie: die erwartete Überraschung, wenn wir die wahre Verteilung verwenden P(x)
2. Kreuzentropie: die erwartete Überraschung, wenn wir die falsche Verteilung Q(x)

Um die KL-Divergenzformel zu bekommen, ziehen wir einfach diese beiden Werte voneinander ab und erhalten das hier: 

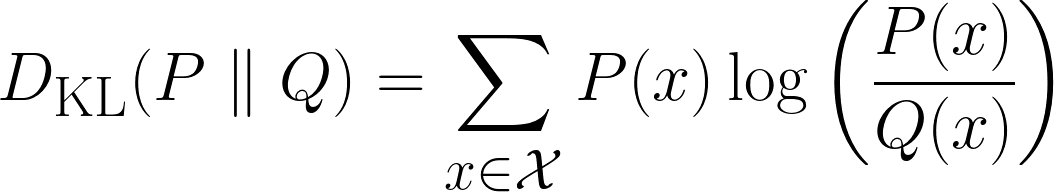
Und ja, du wirst dich fragen, warum? 

Kommen wir zurück zu der Intuition der Überraschung.

• Die Entropie sagt uns , wie groß die Überraschung mindestens sein kann, wenn wir die wahre Verteilung P(x) kennen .. Sieh es einfach als „ideale Kosten“ an.
• Die Kreuzentropie zeigt uns , wie überraschend die Annäherung Q(x)tatsächlich ist . Sieh es einfach als die „echten Kosten“ an.

Wenn wir also die KL-Divergenz berechnen, indem wir diese Werte voneinander abziehen, fragen wir uns, wie viel zusätzliche Überraschung wir zahlen, weil wir die falsche Verteilung Q(x) anstelle der echten Verteilung P(x) verwendet haben . Das ist die Strafe dafür, dass man die falschen Überzeugungen hat.

Wichtig ist auch, dass die KL-Divergenz gleich 0 ist, wenn Q(x) gleich P(x)ist , also wenn die Wahrscheinlichkeitsverteilungen identisch sind (). Das macht Sinn – wenn die Vorhersagen unseres Modells genau mit der echten Verteilung übereinstimmen, gibt'skeine Überraschung und somitauch keine Strafpunkte.

Das ist was anderes als Kreuzentropie, die auch dann nicht auf Null geht, wenn P(x) gleich ist. Q(x); sie ist einfach gleich der Entropie von P(x).

Wir können uns also KL-Divergenz als „verankert” bei Null, was bedeutet, dass sie erst dann zu steigen beginnt, wenn unsere vorhergesagte Verteilung von der tatsächlichen Verteilung abzuweichen beginnt.

Beispiele

Tolle Arbeit beim Ableiten der Gleichung! Um das Ganze besser zu verstehen, schauen wir uns ein Beispiel an. 

Stell dir vor, wir sollen das Lieblingsfilmgenre eines Nutzers vorhersagen. Aus früheren Daten haben wir die wahre Verteilung über die vier Filmgenres (also unsere„ “ P(x)).

Jetzt haben wir zusammen ein Modell entwickelt, das das vorhergesagt hat (das ist also unser Q(x)).

Es gibt eindeutig einen Unterschied in unserer Verteilung, aber wie groß ist er? Hier verwenden wir die KL-Divergenz anhand der folgenden Gleichung:

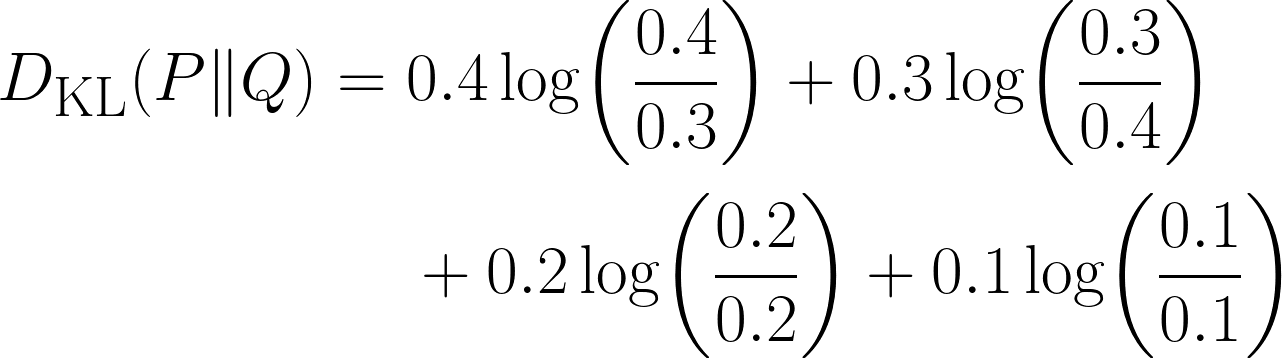
Schau mal, wie der Ausdruck 0 wird, wenn die beiden Verteilungen die gleiche Wahrscheinlichkeit für dieses Ergebnis haben. 

Codierung

Wir können das obige Problem auch mit Python lösen:

import numpy as np
from scipy.stats import entropy      # Important module from scipy

P = np.array([0.4, 0.3, 0.2, 0.1])   # This is our true distribution
Q = np.array([0.3, 0.4, 0.2, 0.1])   # This is our model’s prediction

kl_nats = entropy(P, Q)              # natural log ⇒ nats
kl_bits = entropy(P, Q, base=2)      # log₂ ⇒ bits

print(f"KL(P‖Q) = {kl_nats} nats")
print(f"KL(P‖Q) = {kl_bits} bits")

Dieser Code ist ziemlich einfach und intuitiv, abgesehen davon, dass wir den Begriff KL-Divergenz nirgendwo im Code verwendet haben! Stattdessen habe ichoft die Entropie von verwendet.

Das bringt uns zu einem wichtigen Punkt – KL-Divergenz wird oft als relative Entropie. Deshalb berechnen wir eigentlich die KL-Divergenz, weil das Entropiemodul „ “ die relative Entropie zwischen den beiden Verteilungen berechnet.

Das klingt verwirrend, deshalb mach ich mal kurz Pause und fasse alles zusammen:

Eigenschaften der KL-Divergenz

Nachdem wir unser erstes Beispiel mit der KL-Divergenzformel berechnet haben, wollen wir uns kurz mit einigen ihrer wichtigsten Eigenschaften beschäftigen.

1. Nicht-Negativität: Die KL-Divergenz ist nie negativ. Das macht intuitiv Sinn, da der niedrigste Wert, den es annehmen kann, 0 ist, also wenn unsere vorhergesagte Verteilung genau der tatsächlichen Verteilung entspricht. Und wir können nie negative Kosten haben, weil wir nicht „weniger überrascht“ sein können als die theoretische minimale Überraschung.
2. Auf Null verankert: Die KL-Divergenz gibt uns den Wert Null, wenn unsere vorhergesagte Verteilung mit der tatsächlichen Verteilung übereinstimmt.
3. Einheiten: Bits gegen Nats: Bei der Berechnung der KL-Divergenz verwenden wir Logarithmen. Aber die Basis dieses Logarithmus entscheidet, welche Einheit das Endergebnis hat:

• Wenn wir die Logarithmusbasis 2 nehmen, wird das Ergebnis in Bits gemessen.
• Wenn wir den natürlichen Logarithmus (ln) nehmen, wird das Ergebnis in Nats gemessen (kurz für „natürliche Informationseinheiten“).

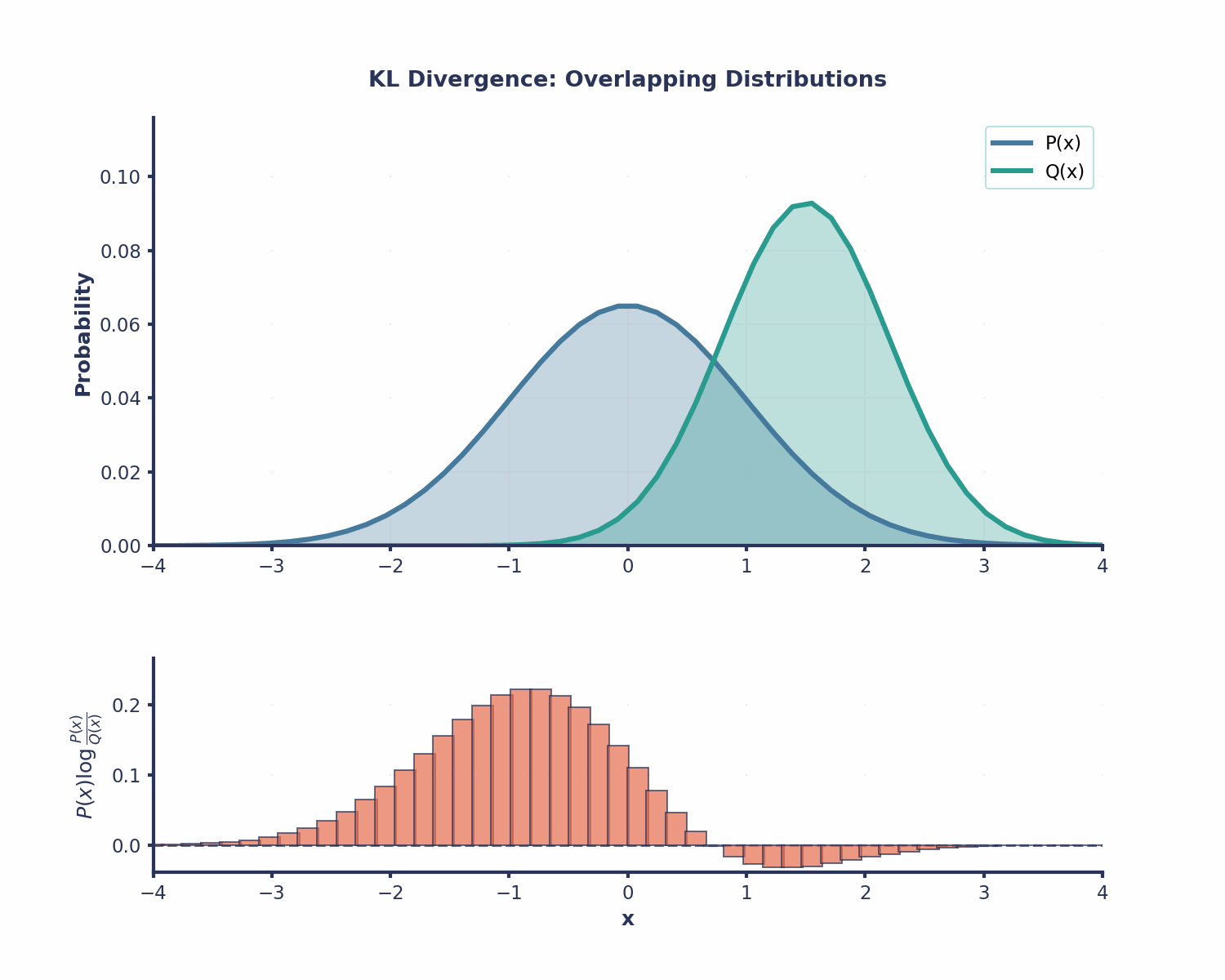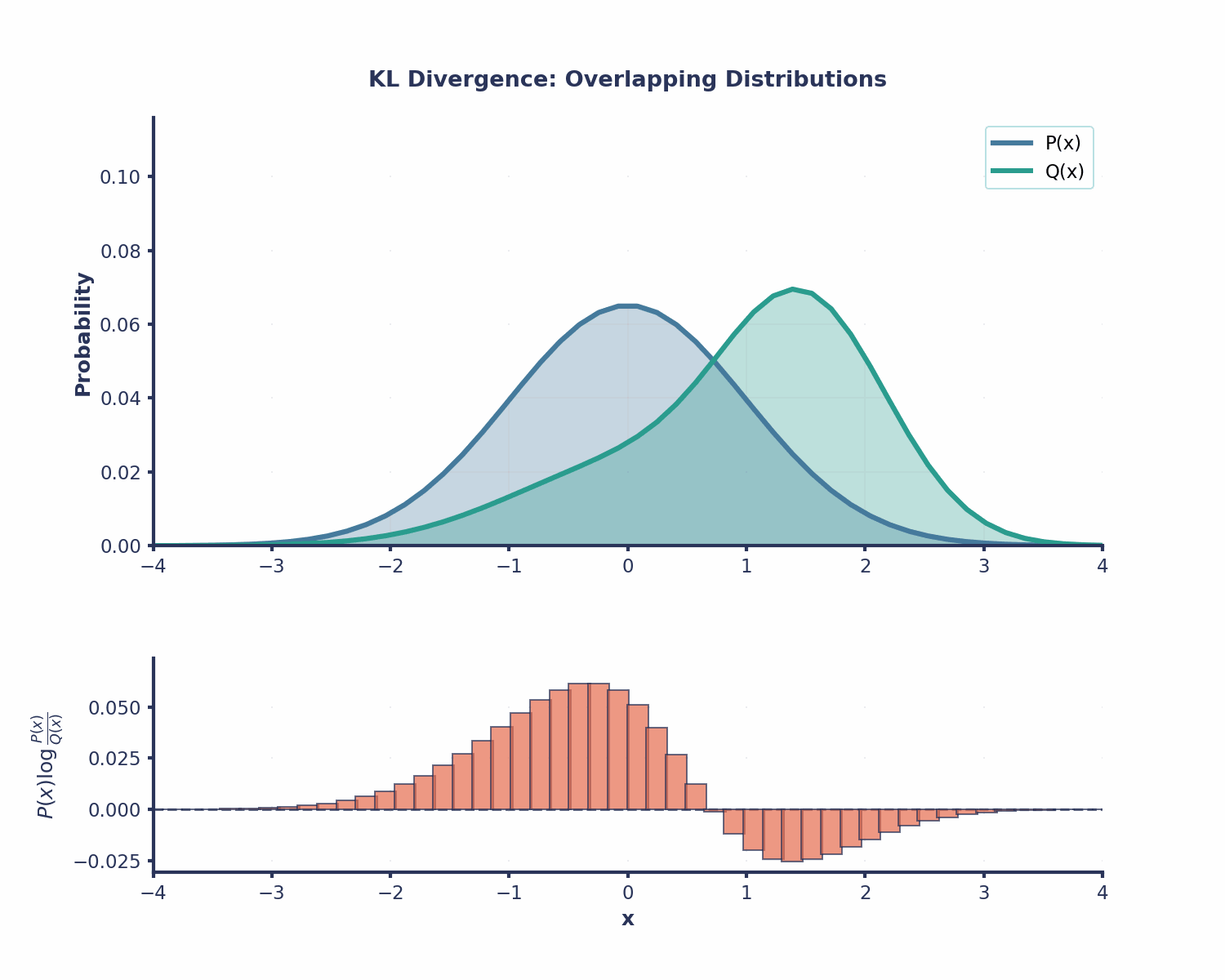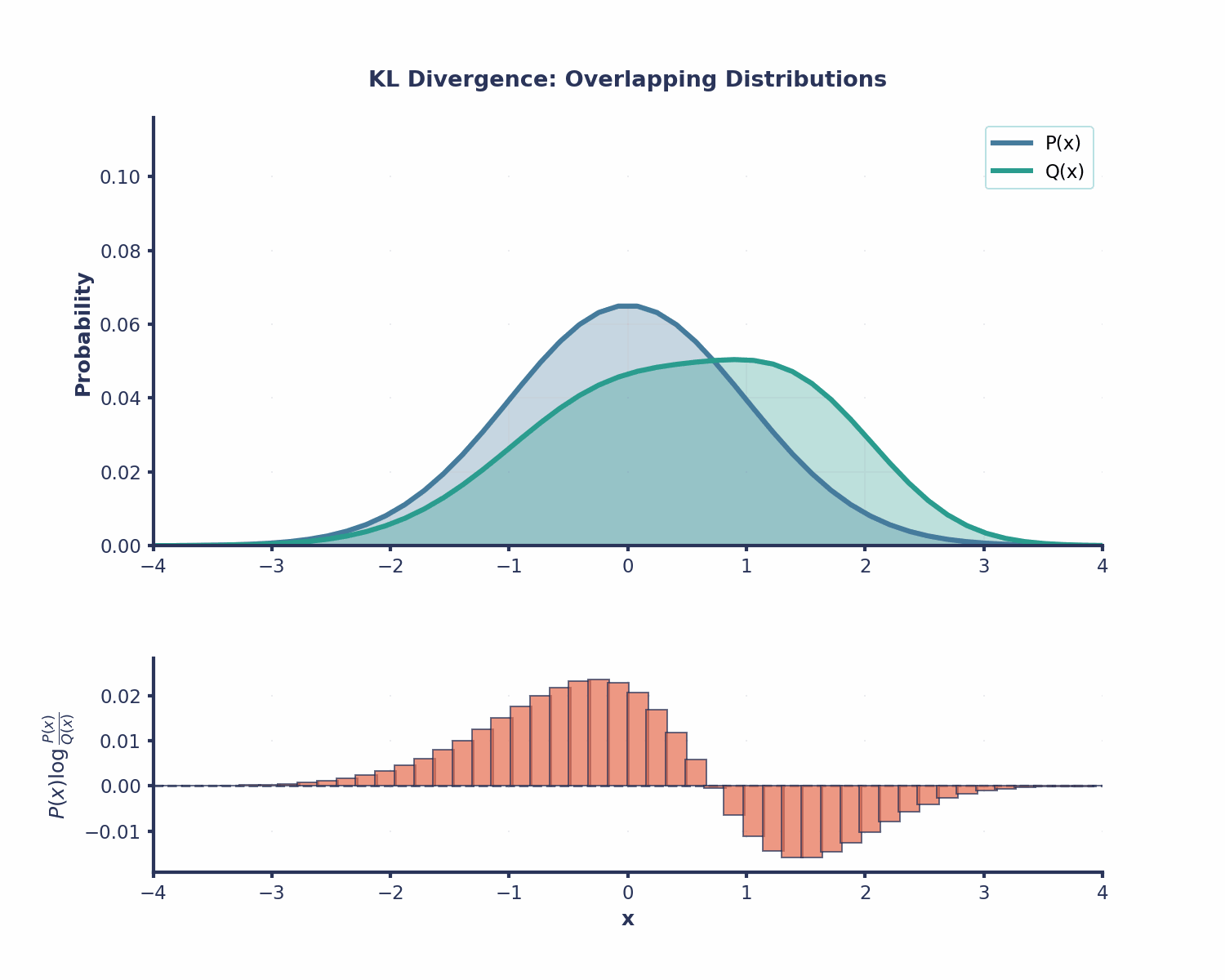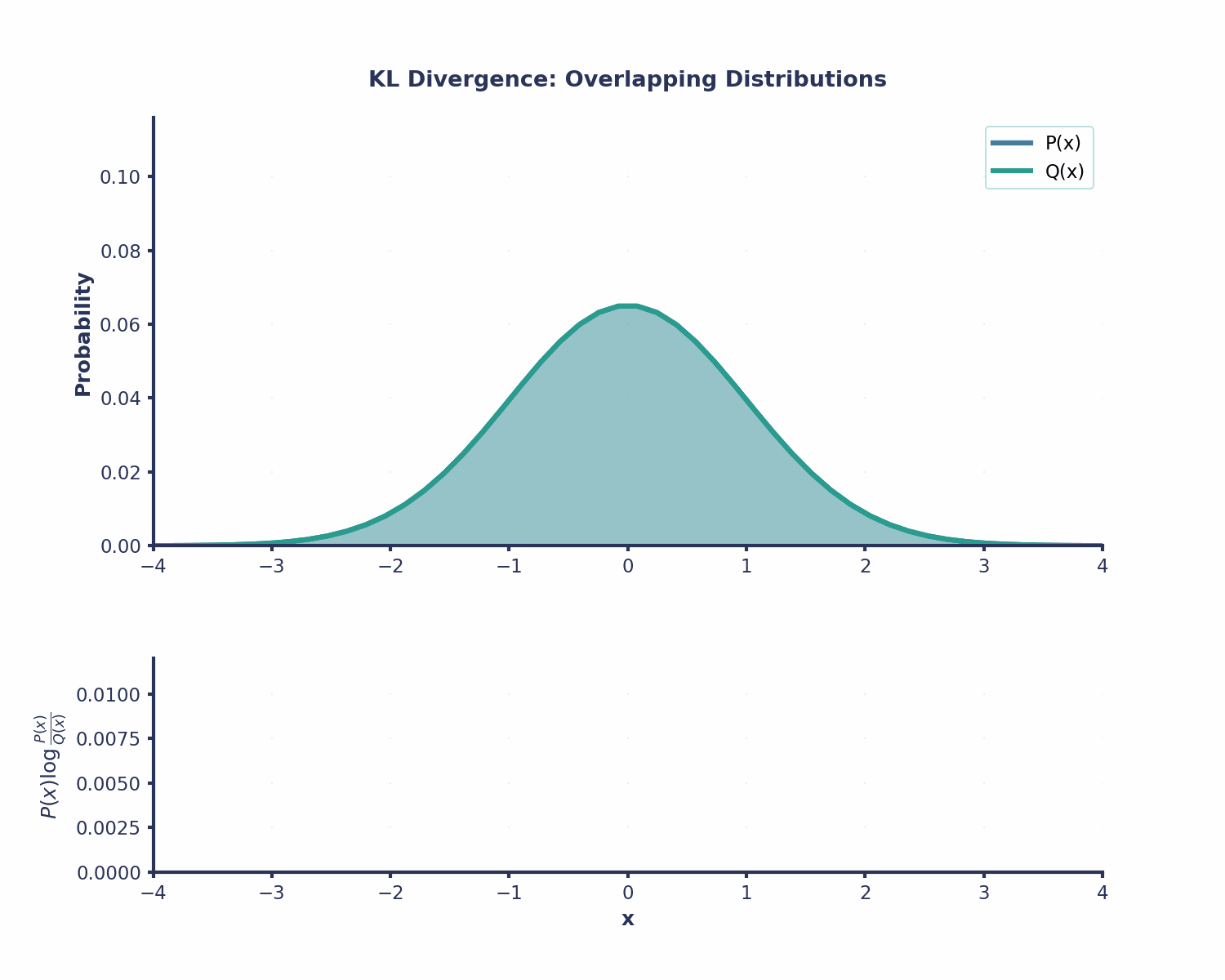
4. Asymmetry: Das ist eine wichtige Eigenschaft – die KL-Divergenz ist nicht symmetrisch. Wenn wir Q(x)mit P(x)annähern , kriegen wir einen anderen Wert als wenn wir Q(x) mit P(x) annähern .. Deshalb ist die KL-Divergenz keine richtige Distanzmessung – sie verhält sich nicht wie normale Distanzen.

Anwendungen der KL-Divergenz im maschinellen Lernen

KL-Divergenz ist in vielen Bereichen des maschinellen Lernens nützlich:

• Modellbewertung: Wie weit deine Vorhersagen von den echten Labels entfernt sind
• Variational Inference: Minimierung von DKL(q(z∣x)∥p(z∣x))D_{\text{KL}}(q(z|x) \| p(z|x))DKL​(q(z∣x)∥p(z∣x)) wie in Variational Autoencoders.
• Verstärkendes Lernen: Die Trust-Region-Policy-Optimierung (TRPO) nutzt KL-Beschränkungen.
• Sprachmodellierung: Vergleich von Token-Vorhersagen mit der tatsächlichen Bedeutung

Einschränkungen der KL-Divergenz und Lösungen 

Wie bei allem gibt's auch bei der KL-Divergenz ein paar Einschränkungen. Schauen wir uns das mal genauer an:

1. Unstimmigkeiten bei der Unterstützung bringen KL zum Explodieren: In seltenen Fällen, in denen Q(x)=0 und P(x)>0 ist, wird der Bruchterm log(P/Q) unendlich groß. Um das zu klären, können wir ε-Glättung hinzufügen oder zur Jensen-Shannon-Divergenz wechseln.
2. Kategoriale Merkmale mit hoher Kardinalität: Mehrere Werte würden zu spärlichen Zählungen und ungenauen KL-Schätzungen führen. Um das zu beheben, können wir seltene Kategorien zusammenlegen oder Bayes'sche Glättung anwenden.
3. Asymmetrie kann echt irreführend sein: Das liegt daran, dass KL(P || Q) und KL(Q || P) nicht denselben Wert ergeben. Eine mögliche Lösung ist die Verwendung der Jensen-Shannon-Divergenz.
4. Einheiten: Oft vergessen wir, die Einheiten der KL-Divergenz anzugeben, was besonders problematisch ist, weil sowohl„ “ als auch „bits “ häufig verwendet werden. Gib also immer die Logarithmusbasis an!

Jensen-Shannon-Divergenz

Du hast vielleicht bemerkt, dass ich schon mal die Jensen-Shannon-Divergenz erwähnt habe, also lass uns das kurz durchgehen. 

Obwohl sie etwas komplizierter und rechenintensiver ist als die KL-Divergenz, ist die Jensen-Shannon-Divergenz symmetrisch. Es ist immer noch keine richtige Entfernungsmessung, weil es die Dreiecksungleichung nicht erfüllt. Wenn wir aber die JS-Divergenz quadratisch mitteln, passt sie zur Dreiecksungleichung und wird zu einer richtigen Metrik. 

Es ist auch eine geglättete Version der KL-Divergenz namens„ ”, die immer zwischen 0 und 1 Bit bleibt (wenn wir die Logarithmusbasis 2 verwenden). Wenn wir uns die Gleichung nochmal anschauen, wird jeder KL-Term gegen den gemeinsamen Mittelpunkt M gemessen, weder P noch Q werden jemals durch Null geteilt, also gibt's auch keine Unendlichkeiten. 

Fazit

Kurz gesagt ist die KL-Divergenz ein wichtiges Tool, mit dem wir die zusätzlichen Informationskosten messen, die entstehen, wenn wir die Verteilung Q unseres Modells für die wahre Verteilung P verwenden. Sie ist null, wenn beide gleich sind, und größer, wenn sie sich unterscheiden, und immer nicht negativ. KL-Divergenz verbindet Entropie und Kreuzentropie und taucht in Verlustfunktionen, Variationsinferenz und Richtlinienbeschränkungen auf. 

KL-Divergence ist zwar super, aber es ist immer noch ein Tool, das wir für Probleme im Zusammenhang mit maschinellem Lernen und Deep Learning verwenden. Um das weiter anzuwenden, check auf jeden Fall unseren Lernpfad „Machine Learning Scientist in Python” und unseren Lernpfad „Maschinelles Lernen für Ingenieure“an, wo beides auf betreutes, unbeaufsichtigtes und tiefes Lernen eingeht.

Wenn du auch bereit bist, KL-Divergenz mit weiteren mathematischen Konzepten zu verbinden, dann schau dir diese Ressourcen an:

• Cross-Entropy-Verlustfunktion beim maschinellen Lernen: Verbesserung der Modellgenauigkeit: Lerne, wie man mit Cross-Entropy die Modellgenauigkeit in Pytorch und Tensorflow optimiert.
• Mathematische Konzepte für Deep Learning verständlich machen: Entdecke die komplette Abdeckung wichtiger mathematischer Konzepte im Deep Learning, zusammen mit Code in Python.
• Datenabweichungen und Modellabweichungen verstehen: Drift-Erkennung in Python: Schau dir an, wie man mit KL-Divergence ein echt wichtiges Problem beim ML lösen kann – die Modelldrift.