Explication de la divergence KL : Intuition, formule et exemples

Dans le domaine de l'apprentissage automatique, il est essentiel de mesurer la précision avec laquelle nos modèles prédisent les résultats dans le monde réel. Que vous développiez un modèle de prévision météorologique ou optimisiez un système de recommandation, vous devez pouvoir quantifier la précision de vos prévisions par rapport à la réalité. Une approche efficace pour y parvenir est la divergence KL.

Dans cet article, j'explorerai ce qu'est la divergence KL, son importance, son interprétation intuitive, ses fondements mathématiques et des exemples pratiques illustrant son application.

Si vous vous intéressez aux concepts du machine learning, je vous recommande vivement de consulter le parcours de compétences « cursus « Principes fondamentaux du machine learning avec Python ».

Qu'est-ce que la divergence KL ?

La divergence KL (divergence de Kullback-Leibler) est une mesure statistique utilisée pour déterminer dans quelle mesure une distribution de probabilité diverge d'une autre distribution de référence.

Supposons que nous construisons ensemble un modèle pour prédire la météo de demain. En arrière-plan, notre modèle effectue des prévisions en attribuant des probabilités aux résultats possibles. Cependant, il est important de se poser la question suivante :

Comment évaluez-vous l'écart entre ces prévisions et la réalité ? 

Nous avons besoin d'un moyen de quantifier cette différence, et c'est là qu'intervient la divergence KL. Il s'agit d'un outil mathématique qui quantifie la différence entre ce que notre modèle estime et ce qui est réellement vrai.

Comme je l'ai déjà mentionné, la divergence KL (ou plus officiellement connue sous le nom de divergence de Kullback-Leibler) est la colonne vertébrale de la science moderne des données, de l'apprentissage automatique et de l'IA. Il nous indique, en bits ou en nats (nous y reviendrons plus tard), le degré de « surprise supplémentaire » ou de « perte d'information » que nous subissons lorsque nous utilisons une distribution de probabilité (par exemple, les prédictions de notre modèle, Q) pour approximer une autre (la réalité, P). 

Il agit comme un juge derrière l'évaluation des modèles, la régularisation dans les réseaux neuronaux, les mises à jour bayésiennes et même la manière dont nous compressons les données ou transmettons efficacement les messages.

Pour bien comprendre l'importance de la divergence KL, considérez-la de la manière suivante. Chaque fois que notre modèle fait une prédiction, il s'agit en réalité d'une simple supposition sur l'avenir. KL-Divergence est le tableau de bord qui permet de calculer le coût de ces paris. Le même principe s'applique à un large éventail de sujets liés à l'apprentissage automatique, qu'il s'agisse de former un chatbot, de diagnostiquer une maladie ou d'optimiser une campagne publicitaire.

Mathématiquement, la divergence KL est définie comme suit :

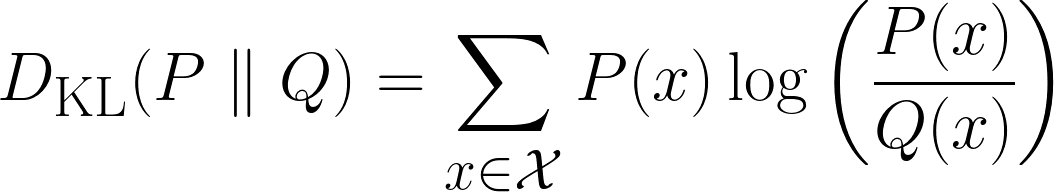
La formule ci-dessus s'applique aux cas discrets, tandis que la formule ci-dessous s'applique aux cas continus.

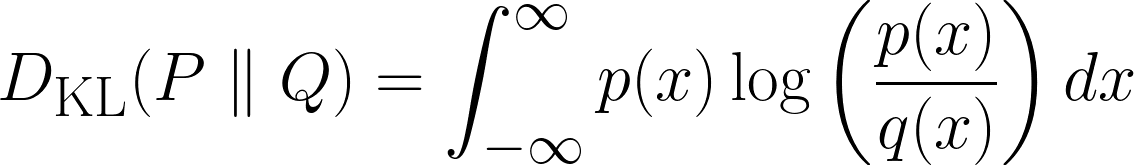
Intuition derrière la divergence KL

Dans cette section, nous allons déduire intuitivement la divergence KL.  Commençons par vous poser une série de questions.

Comprendre la surprise

Si vous lanciez une pièce et que je devinais parfaitement le résultat, seriez-vous surpris ? Je suppose que vous seriez un peu surpris, mais pas complètement choqué. Passons maintenant au deuxième scénario.

Si vous lanciez un dé et que je devine parfaitement le résultat, seriez-vous plus surpris que dans le scénario précédent ? Je suppose que vous répondriez oui, car il est moins probable que je devine le résultat correct.

Maintenant, un dernier scénario :

Si j'avais deviné les numéros gagnants du loto, seriez-vous plus surpris que dans le scénario précédent ? Je suppose que vous répondriez oui et que vous seriez complètement sous le choc. Mais pourquoi ?

En effet, au fur et à mesure que nous avancions dans les scénarios, la probabilité que je devine le résultat correct diminuait, ce qui augmentait votre surprise face au résultat final. Nous venons donc de remarquer une relation :

La probabilité qu'un événement se produise est inversement proportionnelle à l'effet de surprise qu'il produit. 

Pour plus de clarté, plus la probabilité qu'un événement se produise diminue, plus la surprise augmente, et inversement. 

Cependant, nous pouvons faire une autre observation intéressante ici. Si nous revenons aux lancers de dés et imaginons le scénario où vous lancez les mêmes dés trois fois et que je devine correctement à chaque fois, à quel point seriez-vous plus surpris que s'il n'y avait qu'un seul dé et que je devine correctement ? 

Eh bien, votre surprise ne serait pas seulement légèrement supérieure à une seule bonne réponse ; elle serait considérablement plus grande, idéalement trois fois plus grande. Pourquoi ? Car chaque nouvelle supposition correcte renforce votre incrédulité. Il ne s'agit pas simplement d'ajouter un élément de surprise fixe, mais de multiplier l'impression d'incroyable que procure la situation.

Par conséquent, lorsque nous essayons de définir mathématiquement la surprise, nous souhaitons qu'elle présente les caractéristiques suivantes :

1. s des propriétés additives: Si deux événements indépendants se produisent, leur surprise combinée devrait être la somme de leurs surprises individuelles.
1. Exemple : Deviner correctement le résultat d'un lancer de dé → Surprise = S. Deviner correctement le résultat de deux lancers de dé → Surprise = S + S = 2S.
2. Relation inverse avec la probabilité d'. Moins un événement est probable, plus il est surprenant.
1. Exemple : Un tirage au sort (50 %) est moins surprenant que de gagner à la loterie (0,000001 %).
3. Aucune surprise pour certains événements. Si quelque chose se produit systématiquement (probabilité = 1), la surprise devrait être nulle.
1. Exemple : « Le soleil s'est levé aujourd'hui. » → Ce n'est pas surprenant du tout.
4. de mise à l'échelle continue. Une légère modification de la probabilité devrait entraîner un changement progressif et logique du degré de surprise (sans sauts brusques).

À première vue, étant donné le nombre important de conditions requises, on pourrait penser que la définition mathématique sera assez complexe. Cependant, ce n'est pas le cas.

Toutes les exigences ci-dessus peuvent être satisfaites en manipulant la fonction logarithmique. La fonction logarithmique autonome (souvent, log(x) et ln(x) sont utilisés de manière interchangeable) a la forme suivante :

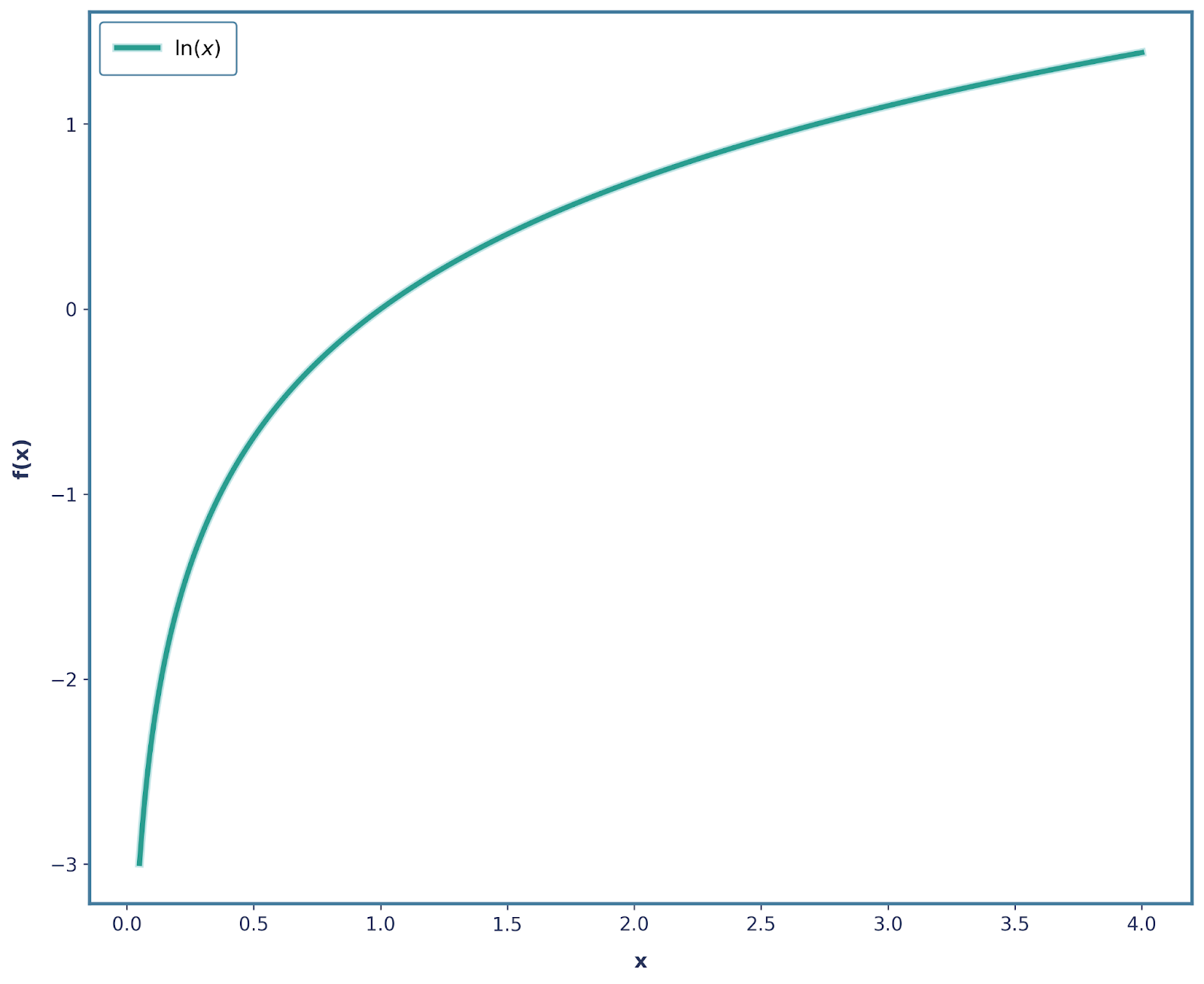
Nous avons déjà satisfait à la plupart de nos exigences. Concentrons-nous d'abord surla propriété additive de l' . Vous vous souvenez que nous avons dit que si deux événements indépendants se produisent, leur surprise totale devrait être la somme de leurs surprises individuelles ? Eh bien, c'est exactement ce que fait la fonction log !

Voici comment procéder :

La probabilité d'obtenir un 6 avec un dé équilibré est de ⅙. Définissons la surprise de l'événement comme suit :

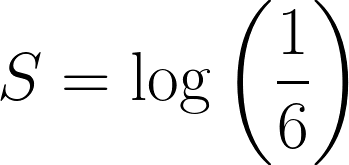
Maintenant, prenons l'exemple où l'on obtient trois fois de suiteun 6 en lançant un dé, la probabilité combinée serait : ⅙ * ⅙ * ⅙ = 1/216. 

En termes de surprise, ce serait :

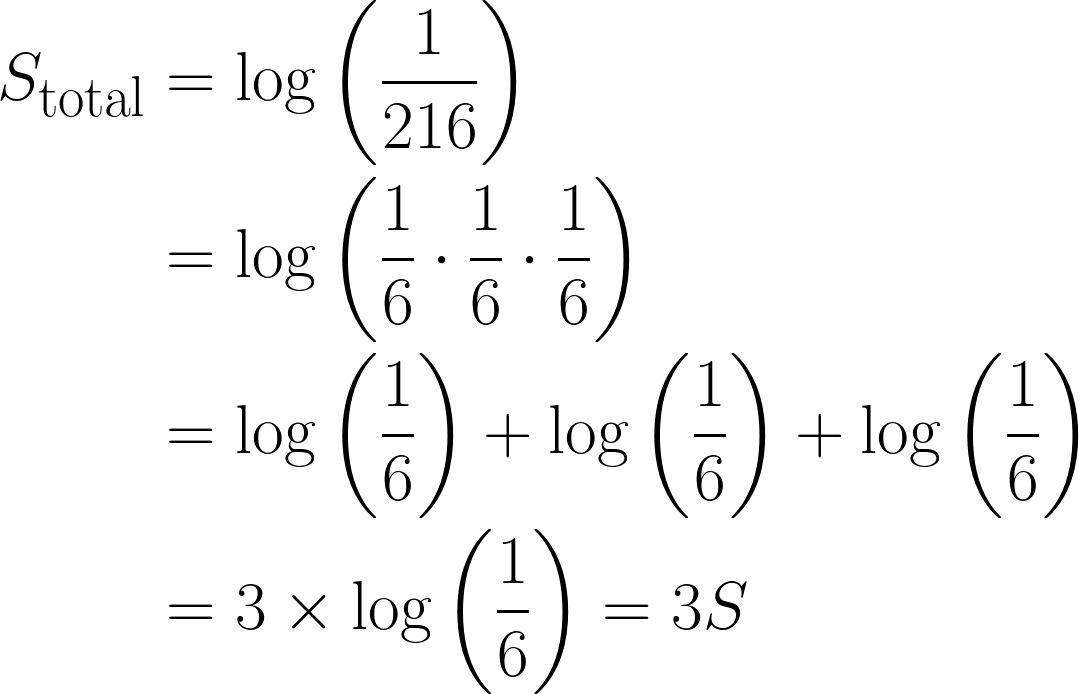
Il s'agit d'une observation importante, car la surprise totale a été multipliée par trois en raison du logarithme utilisé. De plus, cela satisfait également la propriété 3, où log(1) = 0, puisqu'un événement dont la certitude est totale ne comporte aucun élément de surprise. 

De plus, la propriété 4 est également satisfaite, car log(x) est une fonction monotone continue. Cependant, la propriété 2 n'est pas satisfaite, car notre surprise diminue lorsque la probabilité diminue (puisqu'elle devient plus négative). 

Nous pouvons résoudre cela assez facilement en ajoutant un signe négatif. Ainsi, notre fonction est désormais -log(x), qui présente la forme ci-dessous. 

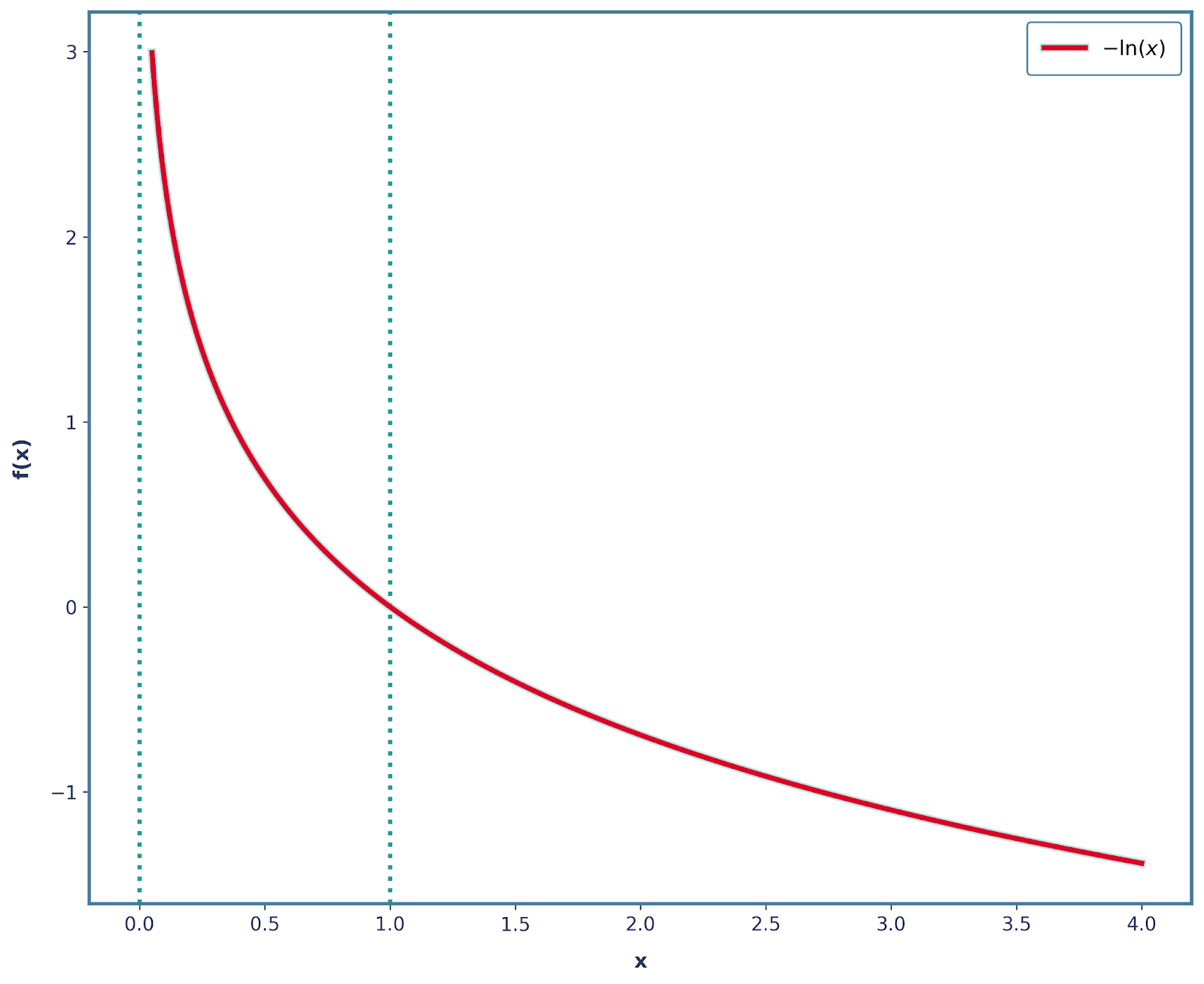
Il est également important de noter que les trois autres propriétés sont toujours satisfaites avec cette modification. Par conséquent, nous pouvons mathématiquement définir la surprise comme suit : 

Entropie

Dans le domaine de l'apprentissage automatique, nous ne nous intéressons pas seulement à la surprise d'un événement unique, mais à la surprise moyenne de tous les événements possibles. C'est ce qu'on appelle la surprise attendue. Plus précisément, nous souhaitons déterminer la surprise attendue de la distribution.

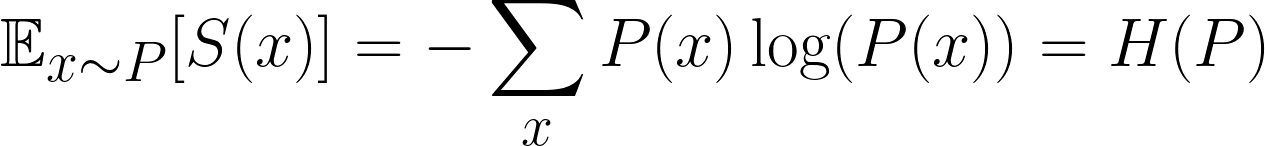
Il s'agit d'une formule bien connue, qui représente la surprise attendue, plus communément appelée entropie. Cependant, il est important de noter que nous utilisons souvent les lettres P et Q pour désigner nos distributions, veuillez donc ne pas les confondre avec la lettre p, qui désigne la probabilité.

Intuitivement, tout ce que nous faisons, c'est multiplier la probabilité de chaque résultat par sa surprise, puis de additionner tous les résultats possibles.

À partir de maintenant, nous allons considérer que P(x) est notre véritable distribution sous-jacente et que Q(x)est la distribution que nous essayons d'approximer à P(x)(c'est-à-dire que Q(X)est la distribution « erronée »). Ceci est très courant dans le domaine de l'apprentissage automatique : nos modèles tentent constamment d'estimer le monde réel.

Maintenant, la question importante se pose :

Que se passe-t-il si nous calculons notre surprise en utilisant une distribution incorrecte ?

Nous pouvons toujours calculer la surprise, mais au lieu d'utiliser P(x), nous la mesurons désormais par rapport à Q(x). Cela nous donne une nouvelle attente :

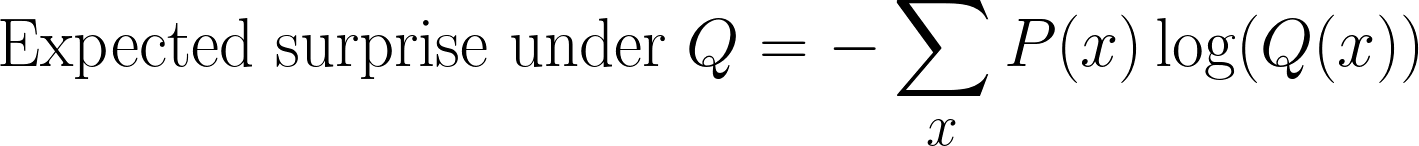
Cette étape peut souvent prêter à confusion lors du calcul de la divergence KL. Nous continuons à échantillonner selon P(x) (car il s'agit de la distribution réelle), mais nous mesurons la surprise à l'aide de Q(x)(la croyance de notre modèle).

Cette quantité est parfois appelée entropie croisée entre P(x)et Q(x).

Formule de divergence KL

Jusqu'à présent, nous avons défini deux grandeurs :

1. Entropie : la surprise attendue si nous utilisons la distribution réelle P(x)
2. Entropie croisée: la surprise attendue si nous utilisons la mauvaise distribution Q(x)

Pour obtenir la formule de la divergence KL, il suffit de soustraire ces deux quantités et d'obtenir ceci : 

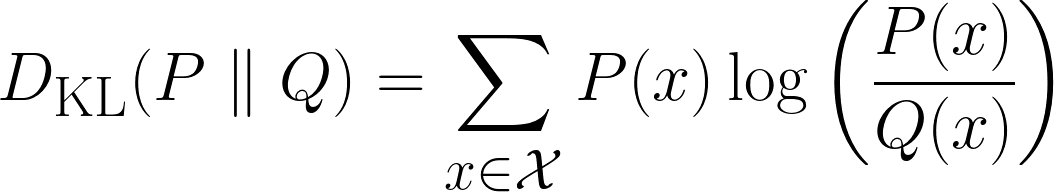
Et oui, la question que vous vous poserez est : pourquoi ? 

Revenons à l'intuition de la surprise.

• L'entropie nous indique le minimum de surprise possible si nous connaissions la distribution réelle P(x) d'. Considérez cela comme le « coût idéal ».
• L'entropie croisée nous indique le degré réel de surprise que nous rencontrons lorsque nous utilisons l'approximation Q(x). Considérez cela comme le « coût réel ».

Ainsi, lorsque nous calculons la divergence KL en soustrayant ces quantités, nous nous demandons quelle surprise supplémentaire nous obtenons parce que nous avons utilisé la distribution incorrecte Q(x) au lieu de la distribution réelle P(x). C'est la conséquence d'avoir des croyances erronées.

Il est également important de noter que si Q(x) est identique à P(x), alors la divergence KL sera égale à 0. Cela est logique : si les prédictions de notre modèle correspondent parfaitement à la distribution réelle, iln'y apas de surprise supplémentaire et donc pas de pénalité.

Ceci diffère de l' l'entropie croisée, qui ne tend pas vers zéro même lorsque P(x) est égal à Q(x); elle est simplement égale à l'entropie de P(x).

Nous pouvons donc considérer la KL-Divergence comme étant « ancrée » à zéro, ce qui signifie qu'elle ne commence à augmenter que lorsque notre distribution prédite commence à diverger de la distribution réelle.

Exemples

Excellent travail pour avoir dérivé l'équation ! Pour mieux comprendre ce concept, prenons un exemple. 

Imaginons que nous ayons pour mission de prédire le genre de film préféré d'un utilisateur. À partir des données passées, nous avons obtenu la distribution réelle des quatre genres de films (c'est-à-dire notre P(x)).

Ensemble, nous avons élaboré un modèle qui a permis de prédire cela (il s'agit de notre Q(x)).

Il existe clairement une différence dans notre répartition, mais de combien ? C'est ici que nous utiliserons la divergence KL, à l'aide de l'équation suivante :

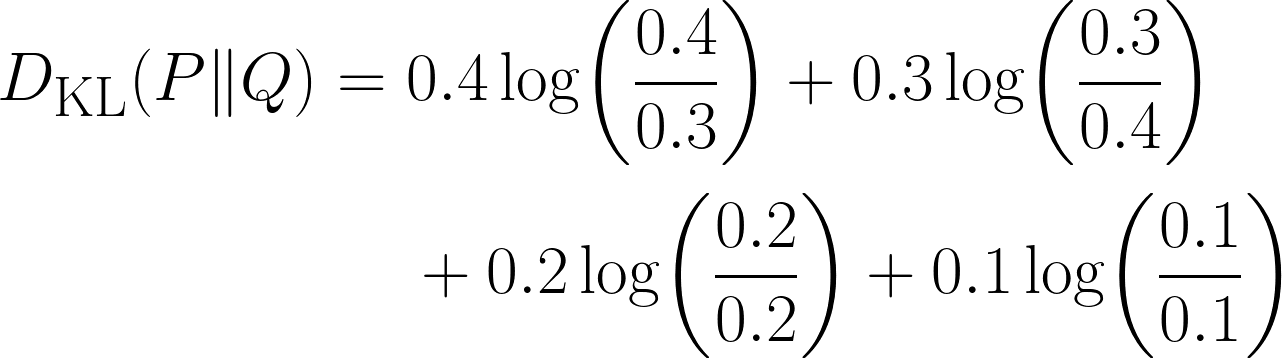
Remarquez que le terme devient égal à 0 lorsque les deux distributions ont la même probabilité pour ce résultat. 

Codage

Nous pouvons également résoudre le problème ci-dessus en utilisant Python :

import numpy as np
from scipy.stats import entropy      # Important module from scipy

P = np.array([0.4, 0.3, 0.2, 0.1])   # This is our true distribution
Q = np.array([0.3, 0.4, 0.2, 0.1])   # This is our model’s prediction

kl_nats = entropy(P, Q)              # natural log ⇒ nats
kl_bits = entropy(P, Q, base=2)      # log₂ ⇒ bits

print(f"KL(P‖Q) = {kl_nats} nats")
print(f"KL(P‖Q) = {kl_bits} bits")

Ce code est assez simple et intuitif, mis à part le fait que nous n'avons utilisé le terme « divergence KL » nulle part dans le code. J'ai plutôt utilisél'entropie d' à plusieurs reprises.

Cela nous amène à un point important : la la divergence KL est souvent appelée entropie relative. Par conséquent, nous calculons en réalité la divergence KL, car le module d'entropie d' calcule l'entropie relative entre les deux distributions.

Cela peut sembler confus, je vais donc faire une petite pause pour résumer tout ce qui a été dit :

Propriétés de la divergence KL

Maintenant que nous avons calculé notre premier exemple à l'aide de la formule de divergence KL, prenons un moment pour explorer certaines de ses propriétés les plus importantes.

1. Absence de négativité : La divergence KL n'est jamais négative. Cela est intuitivement logique, puisque la valeur la plus basse qu'elle peut prendre est 0, ce qui correspond au cas où notre distribution prédite est exactement égale à la distribution réelle. Et nous ne pouvons jamais avoir un coût négatif, car nous ne pouvons pas être « moins surpris » que la surprise minimale théorique.
2. Ancré à zéro : La divergence KL nous donne zéro lorsque notre distribution prévue correspond à la distribution réelle.
3. Unités : Bits contre nats : Lorsque nous calculons la divergence KL, nous utilisons des logarithmes. Cependant, la base de ce logarithme détermine l'unité du résultat final :

• Si nous utilisons la base logarithmique 2, le résultat est mesuré en bits.
• Si nous utilisons le logarithme naturel (ln), le résultat est mesuré en nats (abréviation de « natural units of information », unités naturelles d'information).

4. Asymétrie : Il s'agit d'une propriété importante : la divergence KL n'est pas symétrique. En utilisant Q(x)pour approximer P(x), nous obtenons une valeur différente de celle obtenue en utilisant P(x) pour approximer Q(x). C'est pourquoi la divergence KL ( ) n'est pas une véritable mesure de distance, car elle ne se comporte pas comme les distances habituelles.

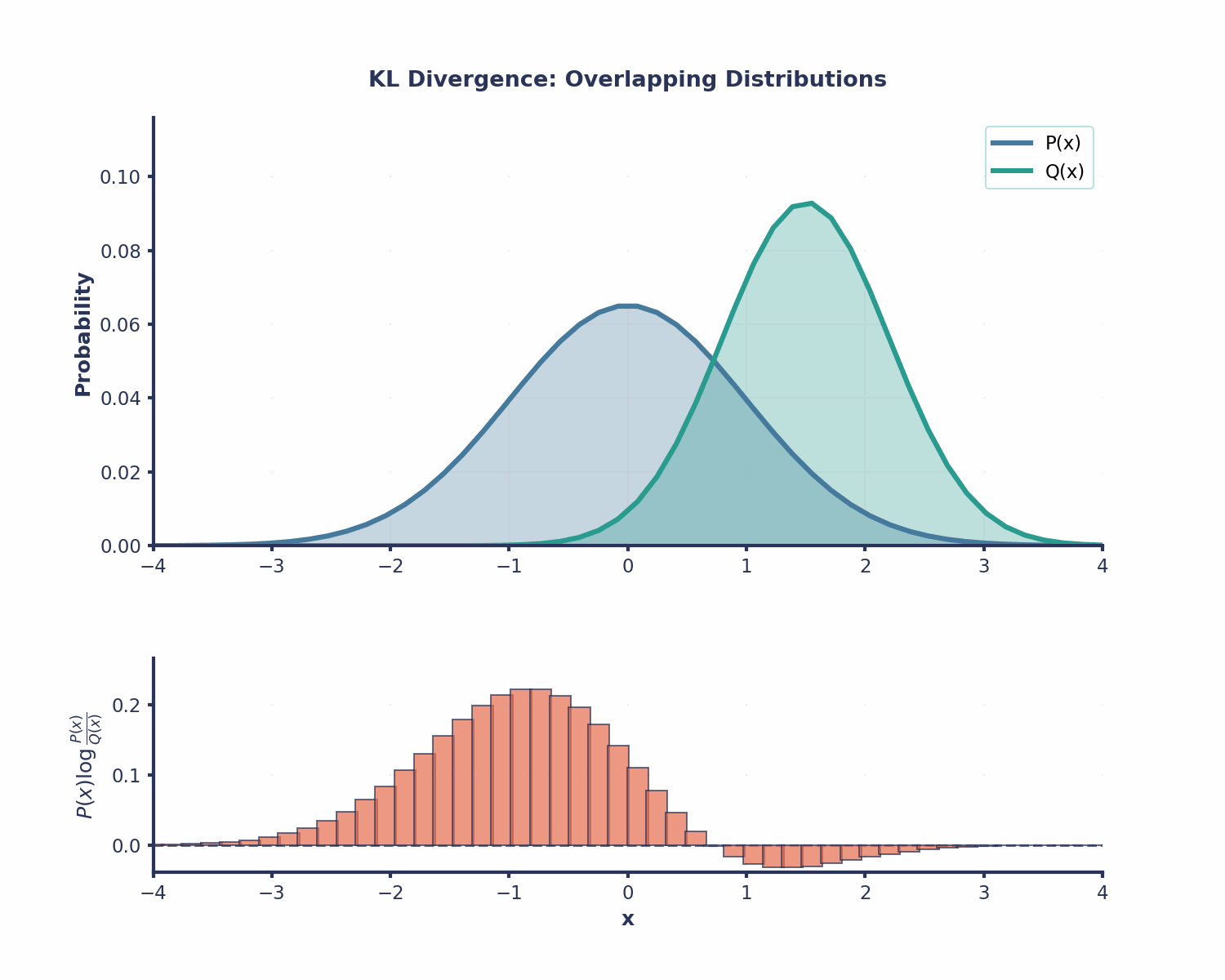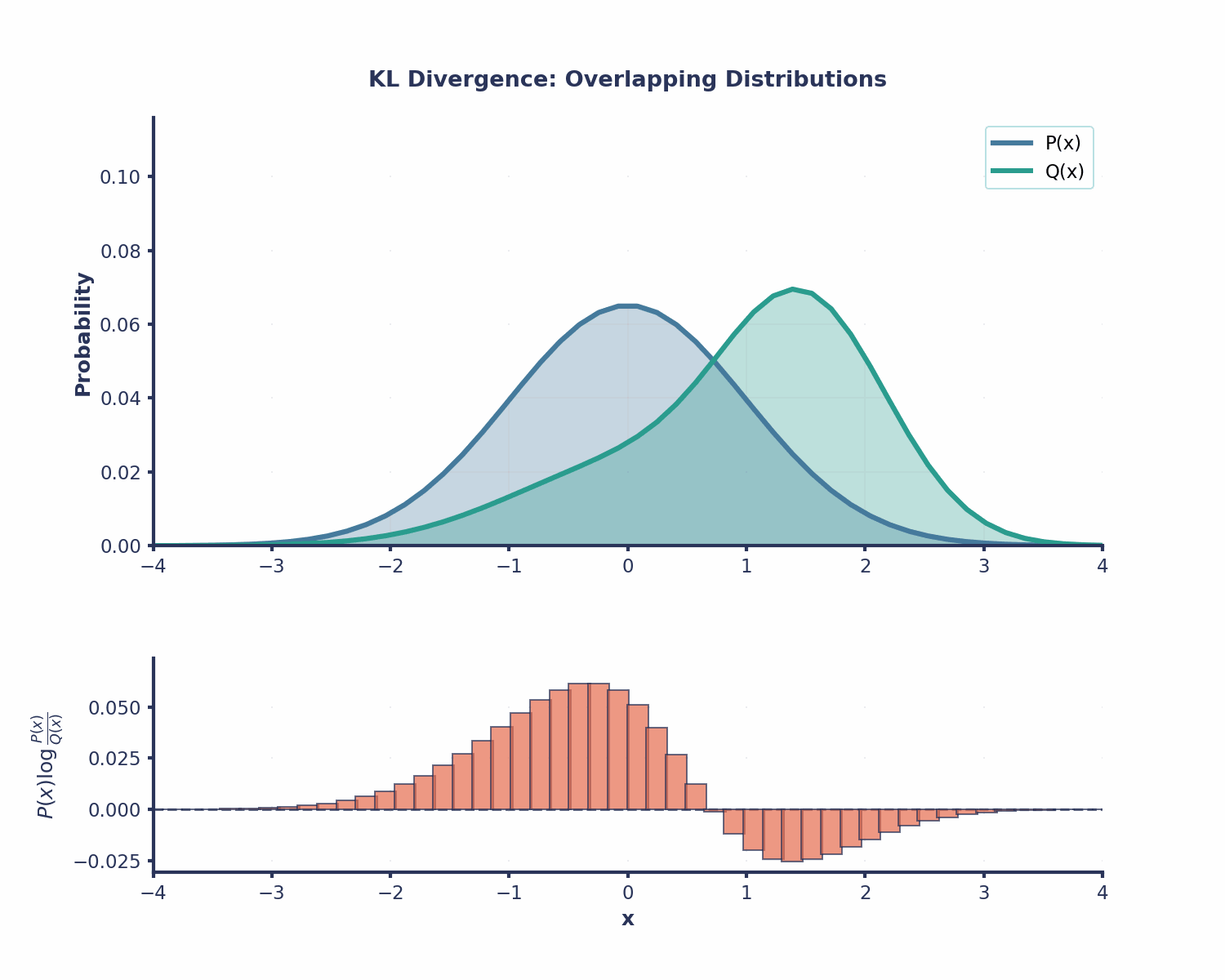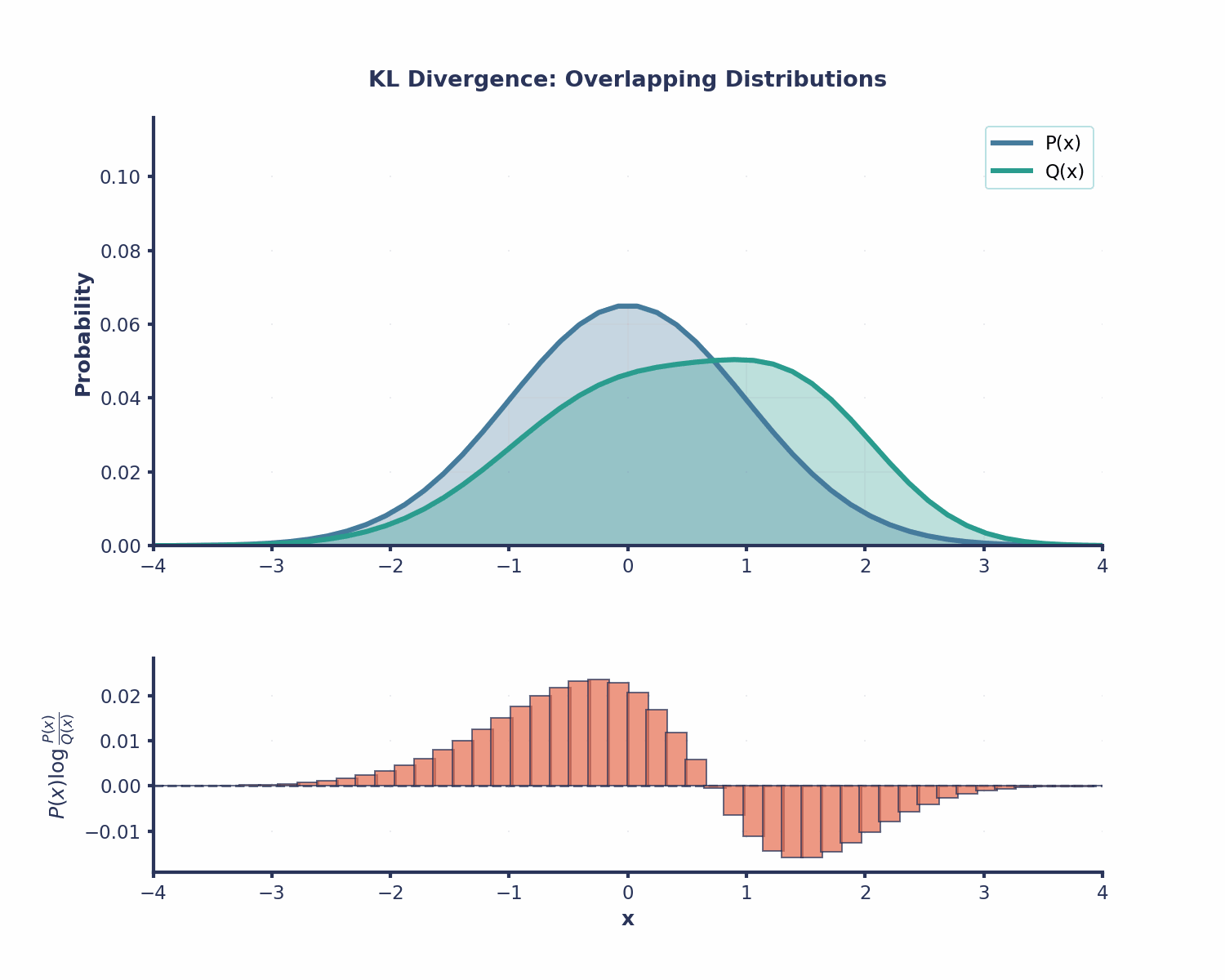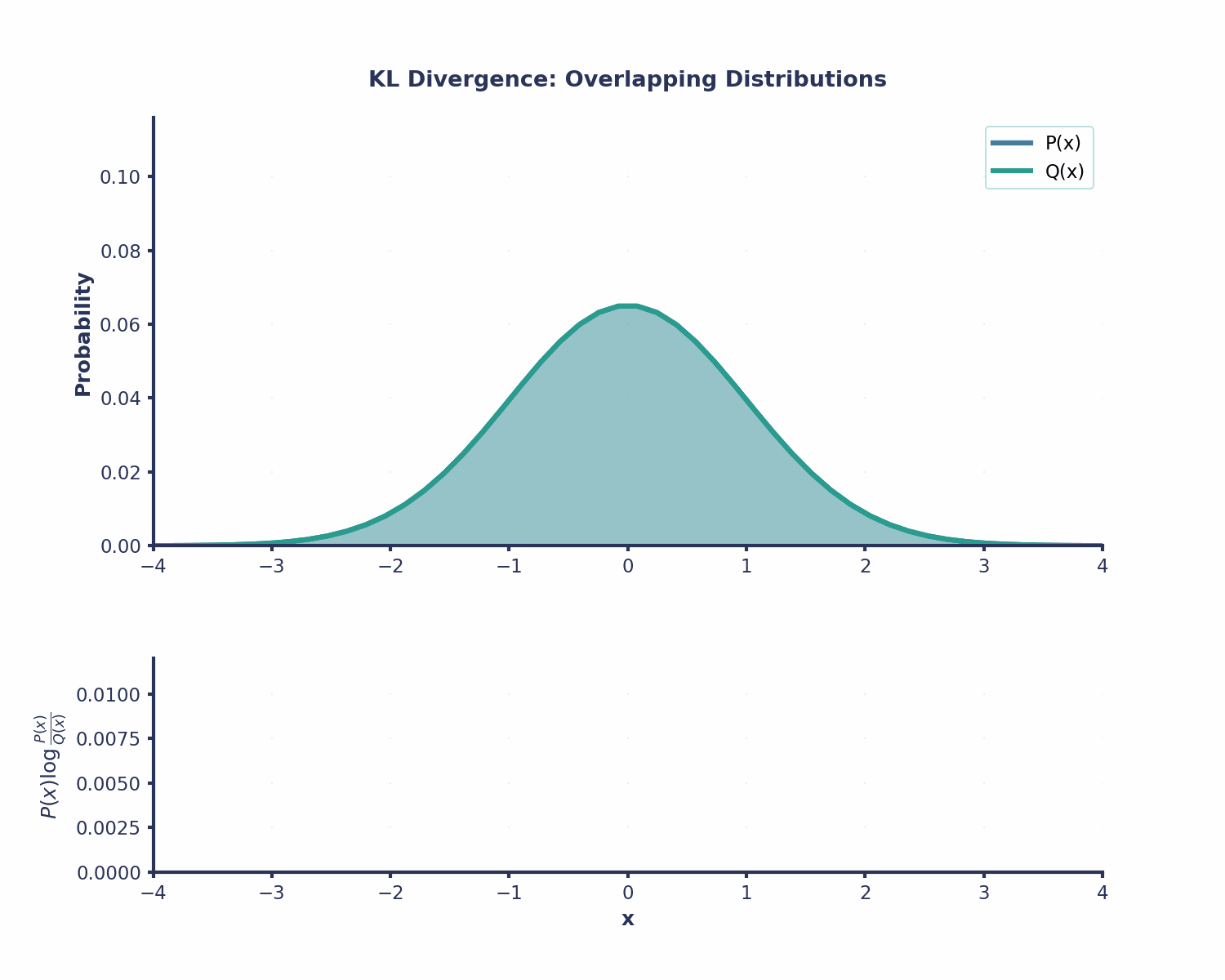
Applications de la divergence KL dans l'apprentissage automatique

La divergence KL est utile dans de nombreux domaines du Machine Learning :

• Évaluation du modèle: mesurer l'écart entre vos prédictions et les étiquettes réelles
• d'inférence variationnelle: minimisation de DKL(q(z∣x)∥p(z∣x))D_{\text{KL}}(q(z|x) \| p(z|x))DKL​(q(z∣x)∥p(z∣x)) comme dans Auto-encodeurs variationnels.
• Apprentissage par renforcement: L'optimisation de la politique de région de confiance (TRPO) utilise des contraintes KL.
• Modélisation linguistique: comparaison des prédictions de tokens avec la vérité terrain

Limites de la divergence KL et solutions 

Comme toute chose, l'utilisation de la divergence KL présente également des limites. Explorons-les en détail :

1. Une incompatibilité fait exploser l'à Kuala Lumpur: Dans de rares cas où Q(x) = 0 et P(x) > 0, le terme fractionnaire log(P/Q) devient infini. Pour résoudre ce problème, nous pouvons ajouter un lissage ε ou passer à la divergence de Jensen-Shannon.
2. de caractéristiques catégorielles à cardinalité élevée: La présence de plusieurs valeurs entraînerait des comptages clairsemés et des estimations KL peu fiables. Pour remédier à cela, nous pouvons fusionner les catégories rares ou appliquer un lissage bayésien.
3. L'asymétrie peut être très trompeuse: En effet, KL(P || Q) et KL(Q || P) ne produisent pas la même valeur. Une solution potentielle consiste à utiliser la divergence de Jensen-Shannon.
4. Unités d': Souvent, nous avons tendance à oublier d'inclure les unités de KL-Divergence, ce qui pose un problème particulier étant donné queles nats ( ) et les bits ( ) sont couramment utilisés. Il est donc important de toujours indiquer la base du logarithme.

divergence de Jensen-Shannon

Vous avez peut-être remarqué que j'ai déjà mentionné la divergence de Jensen-Shannon, nous allons donc rapidement la passer en revue. 

Bien qu'elle soit légèrement plus complexe et plus lourde en termes de calcul que la divergence KL, la divergence de Jensen-Shannon est symétrique. Il ne s'agit toujours pas d'une véritable mesure de distance, car elle ne satisfait pas à l'inégalité triangulaire. Cependant, si nous calculons la racine carrée de la divergence JS, celle-ci satisfait alors à l'inégalité triangulaire et devient une métrique appropriée. 

Il s'agit également d'une versionlissée del', la KL‑divergence, qui reste toujours comprise entre 0 et 1 bit (si nous utilisons la base logarithmique 2). Si nous examinons à nouveau l'équation, chaque terme KL est mesuré par rapport au point médian commun M. Ni P ni Q ne peuvent être divisés par zéro, il n'y a donc pas d'infinis. 

Conclusion

En résumé, la divergence KL est un outil important que nous utilisons pour mesurer le coût supplémentaire en informations que nous supportons lorsque nous substituons la distribution Q de notre modèle à la distribution réelle P. Elle est nulle si les deux distributions sont identiques, et plus grande lorsqu'elles sont différentes, et toujours non négative. La divergence KL relie l'entropie et la cross-entropie, et apparaît dans les fonctions de perte, l'inférence variationnelle et les contraintes de politique. 

KL-Divergence est un excellent outil, mais il reste néanmoins un outil que nous utilisons pour traiter des problèmes liés au Machine Learning et au Deep Learning. Pour pouvoir approfondir ce sujet, veuillez consulter notre cursus Machine Learning Scientist in Python et notre cursus Ingénieur en apprentissage automatique, qui explorent toutes deux l'apprentissage supervisé, non supervisé et profond.

Si vous êtes également prêt à associer la divergence de KL à d'autres concepts mathématiques, veuillez consulter les ressources suivantes :

• Fonction de perte d'entropie croisée dans l'apprentissage automatique : Amélioration de la précision du modèle: Découvrez comment l'entropie croisée est utilisée pour optimiser la précision des modèles dans Pytorch et Tensorflow.
• Démystifier les concepts mathématiques pour l'apprentissage profond: Découvrez une couverture complète des concepts mathématiques importants du Deep Learning, ainsi que du code en Python.
• Comprendre la dérive des données et la dérive des modèles : Détection de dérive en Python: Découvrez comment la divergence KL peut être utilisée pour résoudre un problème important en apprentissage automatique : la dérive des modèles.