Explicación de la divergencia KL: Intuición, fórmula y ejemplos

En machine learning, es fundamental medir la precisión con la que nuestros modelos predicen los resultados del mundo real. Tanto si estás creando un modelo de predicción meteorológica como si estás optimizando un sistema de recomendaciones, necesitas una forma de cuantificar el grado de precisión de tus predicciones con respecto a la realidad. Un enfoque eficaz para lograrlo es la divergencia KL.

En este artículo, exploraré qué es la divergencia KL, por qué es importante, su interpretación intuitiva, sus fundamentos matemáticos y ejemplos prácticos que demuestran su aplicación.

Si estás explorando conceptos de machine learning, te recomiendo encarecidamente que eches un vistazo a la programa «Fundamentos del machine learning en Python».

¿Qué es la divergencia KL?

La divergencia KL (divergencia de Kullback-Leibler) es una medida estadística que se utiliza para determinar en qué medida una distribución de probabilidad se desvía de otra distribución de referencia.

Supongamos que estamos construyendo juntos un modelo para predecir el tiempo que hará mañana. En segundo plano, nuestro modelo está haciendo apuestas: asignando probabilidades a los posibles resultados. Pero aquí hay una pregunta importante que debes hacerte:

¿Cómo miden lo lejos que están esas apuestas de la realidad? 

Necesitamos una forma de cuantificar esta diferencia, y aquí es donde entra en juego la divergencia KL. Es una herramienta matemática que cuantifica la diferencia entre lo que cree nuestro modelo y lo que es realmente cierto.

Como he mencionado anteriormente, la divergencia KL (o, más formalmente, divergencia de Kullback-Leibler) es la columna vertebral de la ciencia de datos moderna, el machine learning y la IA. Nos indica, en bits o nats (más adelante se ofrece más información al respecto), cuánta «sorpresa adicional» o «pérdida de información» se produce cuando utilizas una distribución de probabilidad (por ejemplo, las predicciones de tu modelo, Q) para aproximarte a otra (la realidad, P). 

Actúa como juez detrás de la evaluación de modelos, la regularización en redes neuronales, las actualizaciones bayesianas e incluso la forma en que comprimimos datos o transmitimos mensajes de manera eficiente.

Para comprender realmente la importancia de la divergencia KL, piénsalo de esta manera. Cada vez que nuestro modelo hace una predicción, en realidad solo está apostando por el futuro. KL-Divergence es la tarjeta de puntuación que calculará cuán costosas son esas apuestas. El mismo principio se aplica a una amplia gama de temas relacionados con el machine learning, como la formación de un chatbot, el diagnóstico de una enfermedad o la optimización de una campaña publicitaria.

Matemáticamente, la divergencia KL se define así:

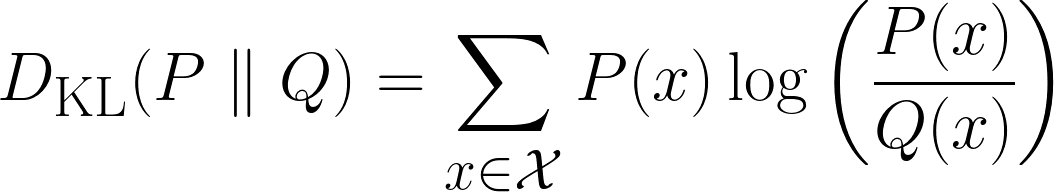
Arriba se muestra la fórmula para casos discretos, y la fórmula de abajo es para casos continuos.

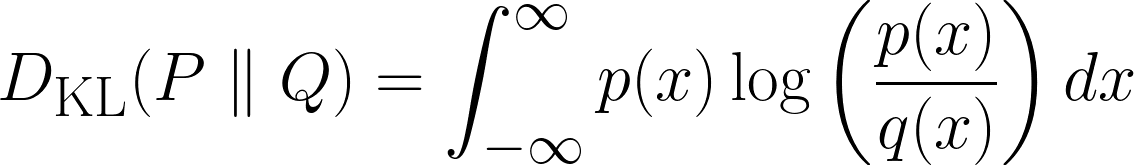
La intuición detrás de la divergencia KL

En esta sección, derivaremos intuitivamente la divergencia KL.  Empecemos por hacerte una serie de preguntas.

Comprender la sorpresa

«Si lanzaras una moneda al aire y yo adivinara perfectamente el resultado, ¿te sorprendería?». Supongo que te sorprendería un poco, pero no te escandalizaría del todo. Ahora, pasemos al segundo escenario.

«Si tú tiraras un dado y yo adivinara perfectamente el resultado, ¿te sorprendería más que en el caso anterior?». Supongo que dirías que sí, ya que es menos probable que yo adivine el resultado correcto.

Ahora, un último escenario:

«Si hubiera adivinado correctamente los números ganadores de la lotería, ¿estarías más sorprendido que en el escenario anterior?». Supongo que dirías que sí y te quedarías completamente en shock. ¿Pero por qué?

Esto se debe a que, a medida que avanzábamos en los escenarios, la probabilidad de que yo adivinara el resultado correcto disminuía y, por lo tanto, tu sorpresa ante el resultado aumentaba. Así que acabamos de observar una relación:

La probabilidad de que ocurra un evento tiene una relación inversa con la sorpresa. 

Para mayor claridad, a medida que la probabilidad de que algo ocurra disminuye, la sorpresa aumenta, y viceversa. 

Sin embargo, podemos hacer otra observación interesante aquí. Si volvemos a los lanzamientos de dados e imaginamos la situación en la que tú lanzas los mismos dados tres veces y yo adivino correctamente cada vez, ¿cuánto más te sorprendería que si solo hubiera un dado y yo adivinara correctamente? 

Bueno, tu sorpresa no sería solo un poco mayor que la de haber acertado una sola respuesta, sino que sería mucho mayor, idealmente tres veces mayor. ¿Por qué? Porque cada nueva suposición correcta aumenta tu incredulidad. No se trata solo de añadir una cantidad fija de sorpresa, sino de multiplicar lo increíble que parece la situación.

Por lo tanto, al intentar definir matemáticamente la sorpresa, querríamos que tuviera:

1. Propiedad aditiva: Si ocurren dos eventos independientes, tu sorpresa combinada debería ser la suma de tus sorpresas individuales.
1. Ejemplo: Adivinar correctamente 1 tirada de dado → Sorpresa = S. Adivinar correctamente 2 tiradas de dado → Sorpresa = S + S = 2S.
2. Relación inversa con la probabilidad. Cuanto menos probable es un acontecimiento, más sorprendente resulta.
1. Ejemplo: Lanzar una moneda al aire (50 %) es menos sorprendente que ganar la lotería (0,000001 %).
3. Sin sorpresas en determinados eventos. Si algo ocurre siempre (probabilidad = 1), la sorpresa debería ser cero.
1. Ejemplo: «Hoy ha salido el sol». → No es ninguna sorpresa.
4. Escalado continuo. Un pequeño cambio en la probabilidad debería dar lugar a un cambio suave y lógico en la sorpresa (sin saltos repentinos).

A primera vista, dado que hay muchos requisitos, podríamos pensar que la definición matemática será bastante complicada. ¡Pero no es así!

Todos los requisitos anteriores se pueden resolver manipulando la función logarítmica. La función log independiente (muchas veces, log(x) y ln(x) se utilizan indistintamente) tiene la siguiente forma:

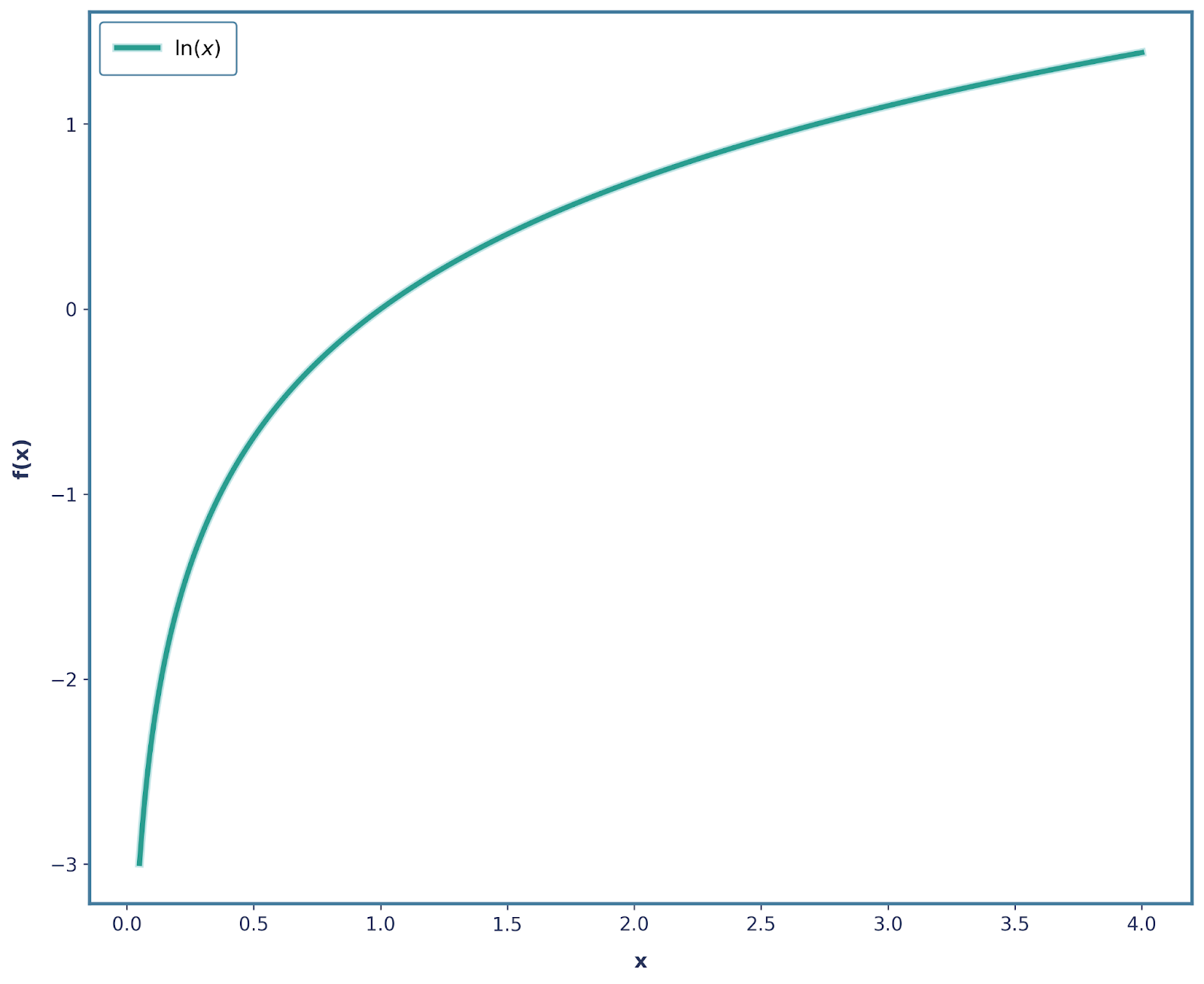
Ya hemos cumplido muchos de nuestros requisitos. Centrémonos primero enla propiedad aditiva de la función e . ¿Recuerdas que dijimos que si ocurren dos eventos independientes, su sorpresa total debería ser la suma de sus sorpresas individuales? ¡Pues eso es exactamente lo que hace la función log!

Así es como se hace:

La probabilidad de sacar un 6 en un dado imparcial es ⅙ , y definamos la sorpresa del evento como esto:

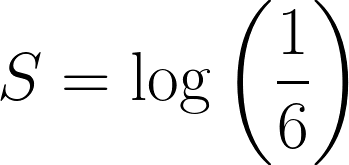
Ahora, tomemos el caso de sacar un 6 tres veces seguidas, la probabilidad combinada sería: ⅙ * ⅙ * ⅙ = 1/216. 

En términos de sorpresa, sería:

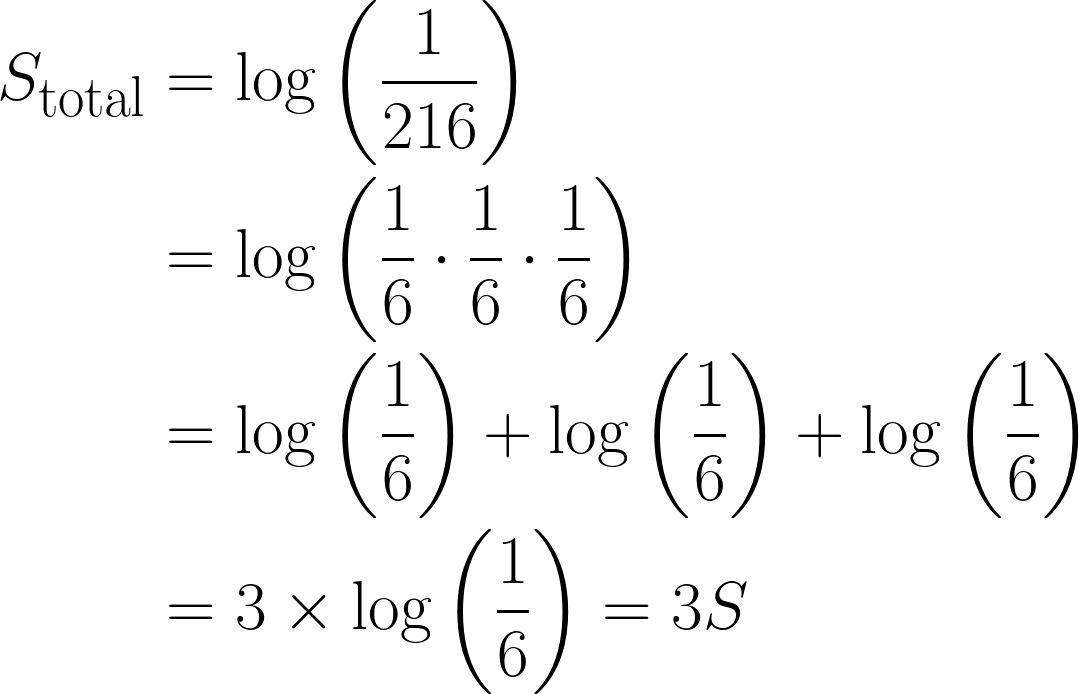
Esta es una observación bastante importante, ya que la sorpresa total se ha multiplicado por tres debido al logaritmo que hemos utilizado. Además, esto también satisface la Propiedad 3, donde log(1) = 0, ya que un evento con certeza total no tiene ningún elemento sorpresa. 

Además, la propiedad 4 también se cumple, ya que log(x) es una función monótona continua. Sin embargo, la propiedad 2 no se cumple, ya que nuestra sorpresa disminuye cuando la probabilidad disminuye (ya que se vuelve más negativa). 

Podemos resolver esto fácilmente aplicando un signo negativo. Por lo tanto, nuestra función ahora es -log(x), que tiene la siguiente forma. 

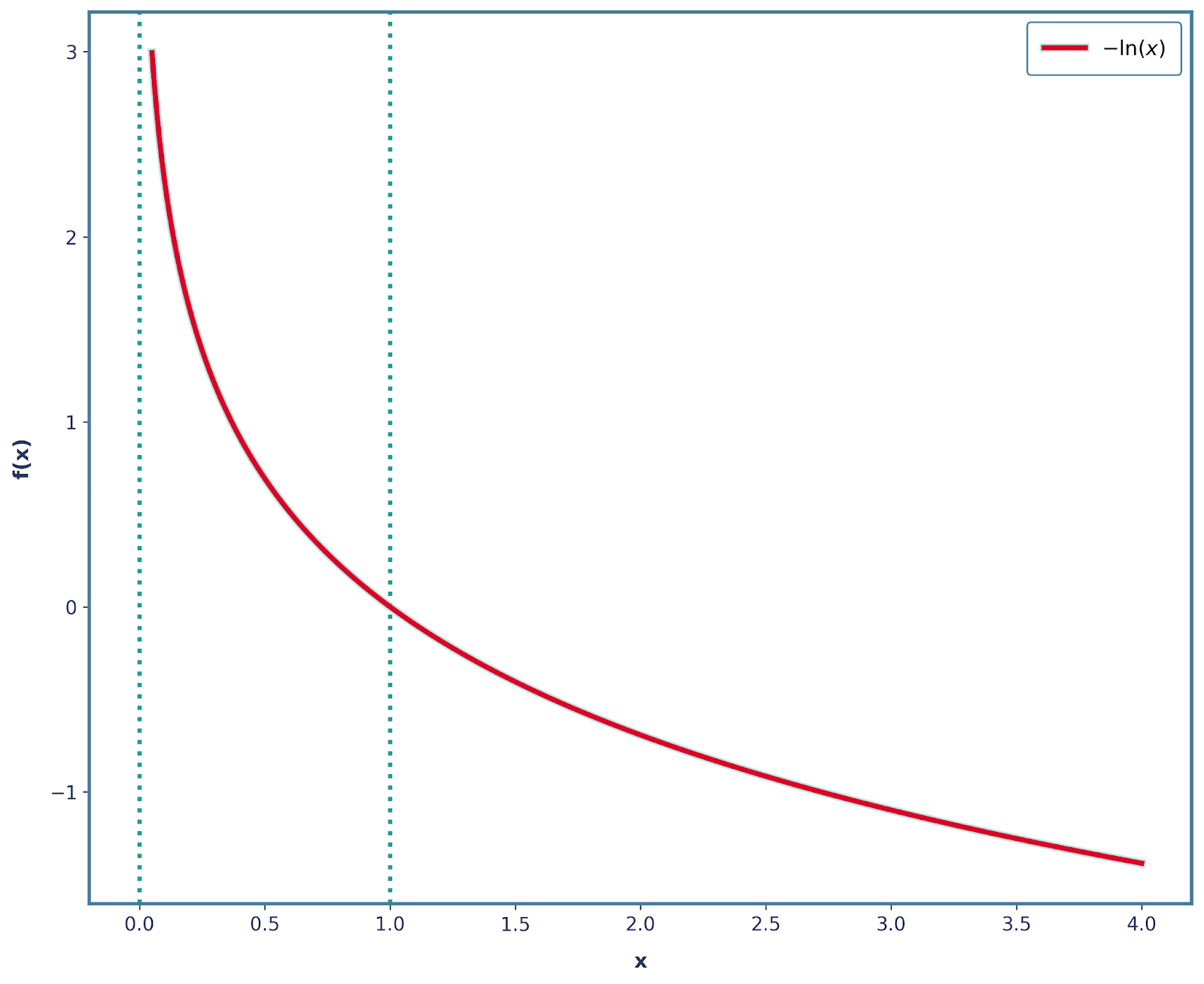
También es importante señalar que las otras tres propiedades también se siguen cumpliendo con este cambio. Por lo tanto, podemos definir matemáticamente la sorpresa como: 

Entropía

En machine learning, no nos interesa solo la sorpresa de un evento único, sino la sorpresa promedio en todos los eventos posibles. A eso se le llama la sorpresa esperada. Más concretamente, nos interesa encontrar la sorpresa esperada de la distribución.

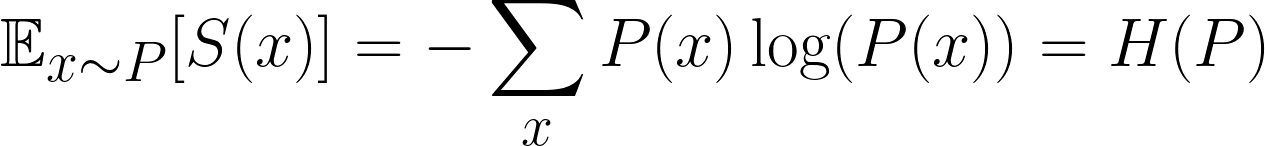
Esta es una fórmula famosa, y es la sorpresa esperada, o más comúnmente conocida como Entropía. Sin embargo, resulta bastante confuso que a menudo utilicemos P y Q para denotar nuestras distribuciones, ¡así que no te confundas con p, que denota probabilidad!

Intuitivamente hablando, lo único que hacemos es multiplicar la probabilidad de cada resultado por su sorpresay, a continuación, sumándola todos los resultados posibles.

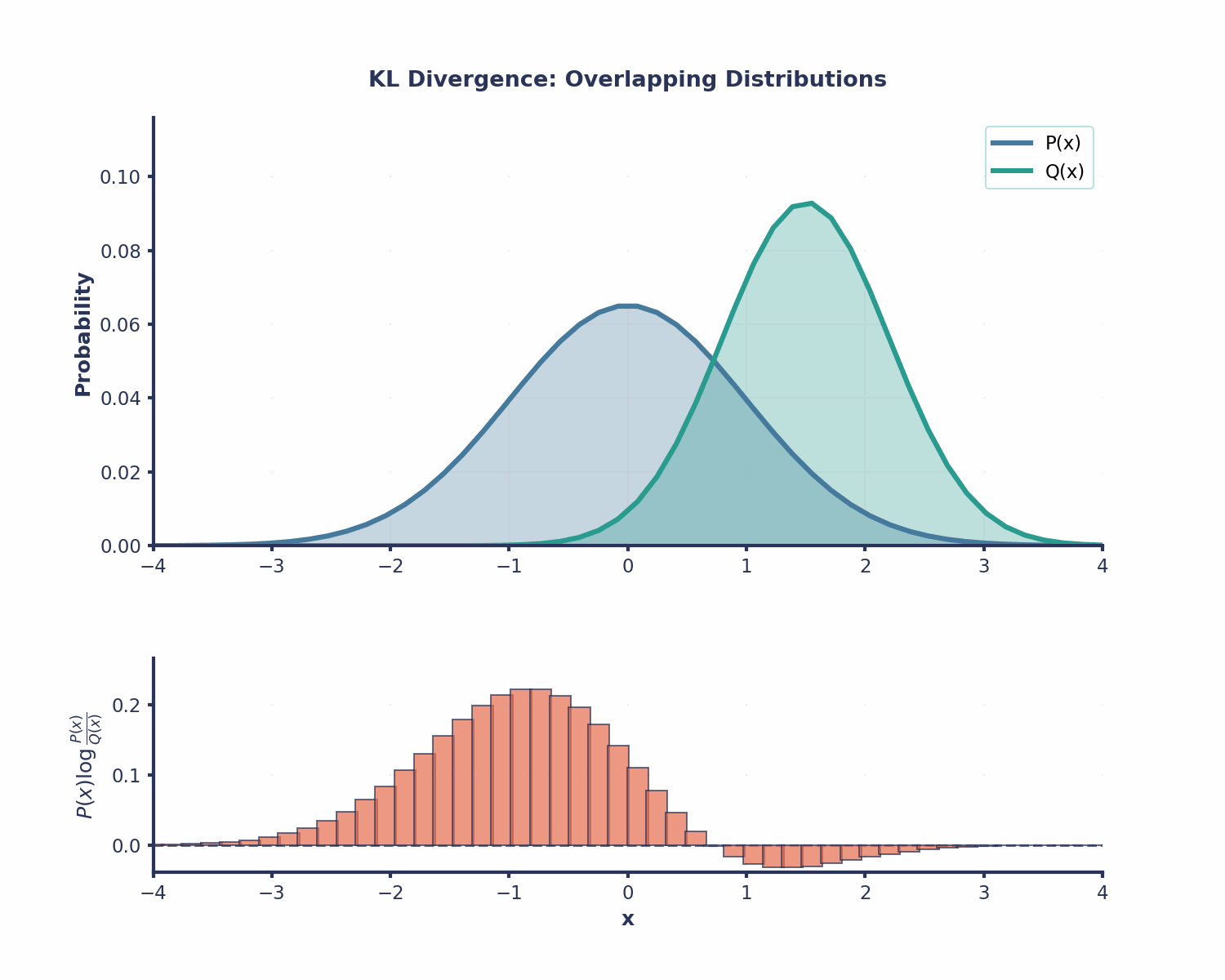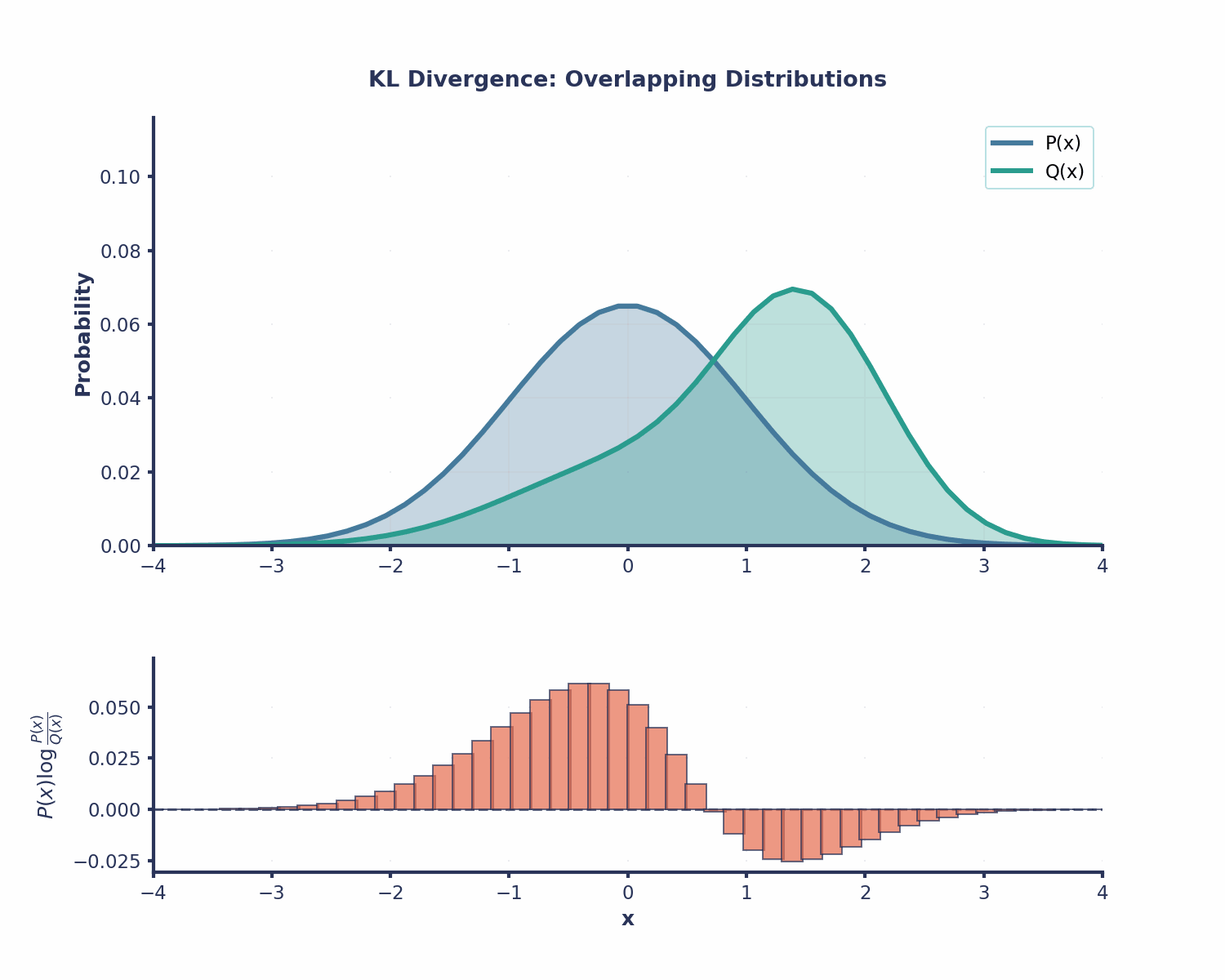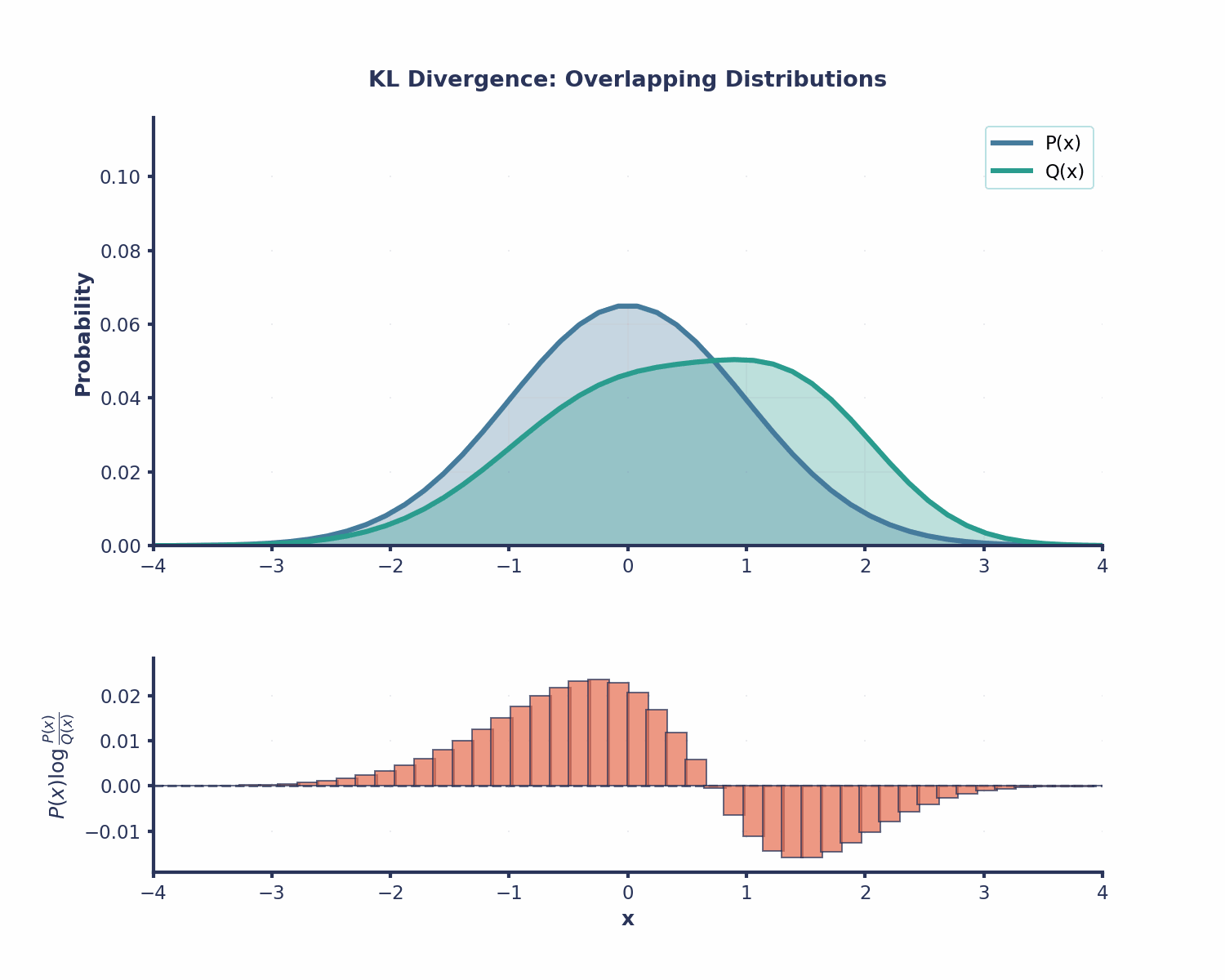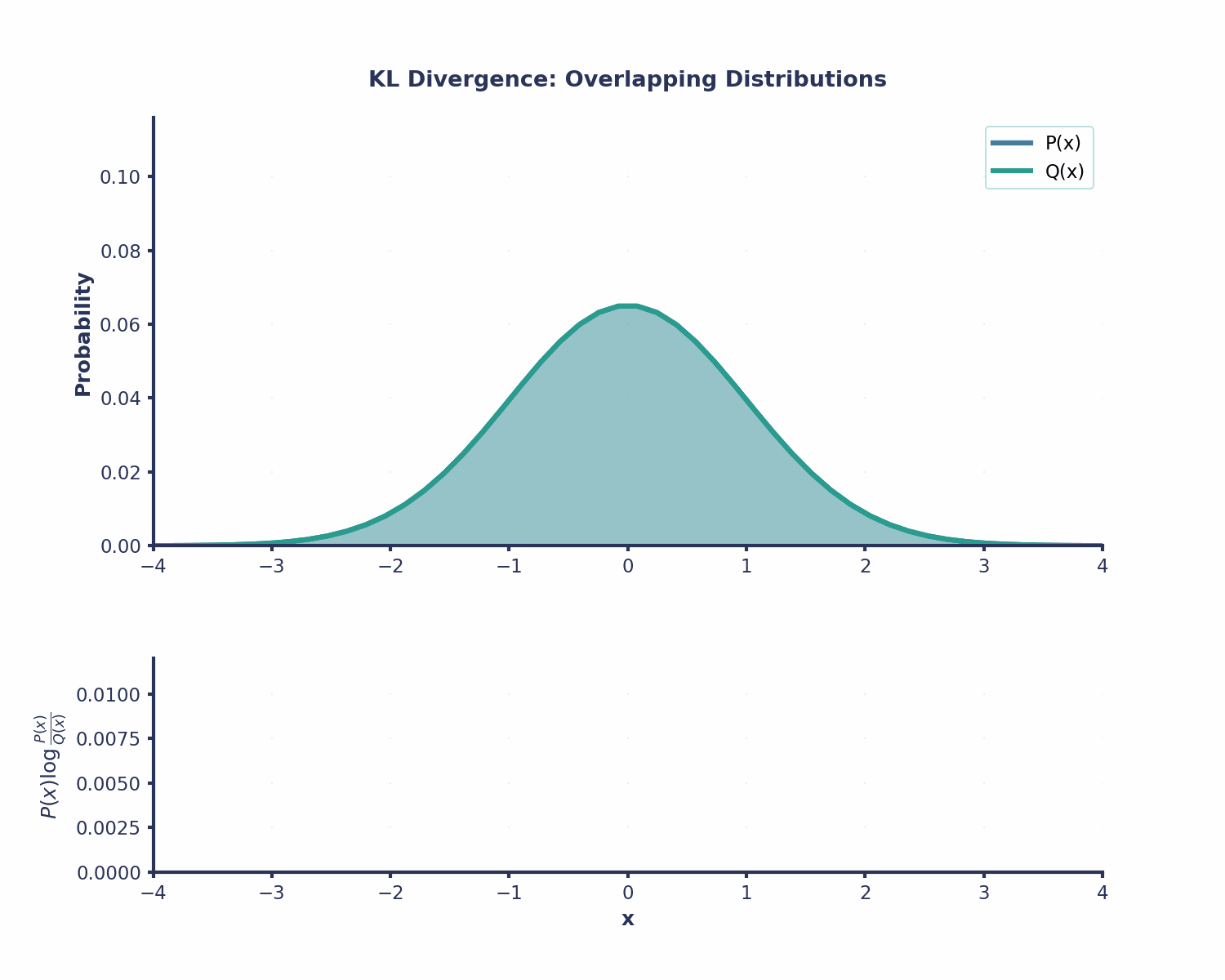
A partir de este momento, vamos a establecer que P(x) es nuestra distribución subyacente real y Q(x)es la distribución con la que intentamos aproximar P(x)(es decir, Q(X)es la distribución «incorrecta»). Esto es muy común en el machine learning: nuestros modelos intentan constantemente estimar el mundo real.

Ahora viene la gran pregunta:

¿Qué ocurre si calculamos nuestra sorpresa utilizando una distribución incorrecta?

Todavía podemos calcular la sorpresa, pero en lugar de utilizar P(x), ahora la medimos con respecto a Q(x). Esto nos da una nueva expectativa:

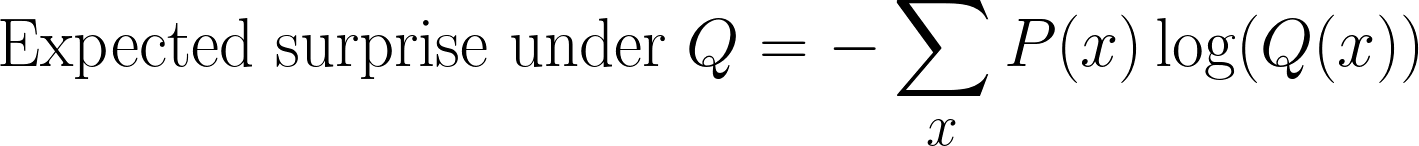
Este paso suele resultar confuso al derivar la divergencia KL. Seguimos tomando muestras según P(x) (porque esa es la distribución real), pero medimos la sorpresa utilizando Q(x)(la creencia de nuestro modelo).

Esta cantidad se denomina a veces entropía cruzada entre P(x)y Q(x).

Fórmula de divergencia KL

Hasta ahora, hemos definido dos magnitudes:

1. Entropía: la sorpresa esperada si utilizamos la distribución real P(x)
2. Entropía cruzada: la sorpresa esperada si utilizas el incorrecta distribución Q(x)

Para obtener la fórmula de la divergencia KL, simplemente restamos estas dos cantidades y obtenemos lo siguiente: 

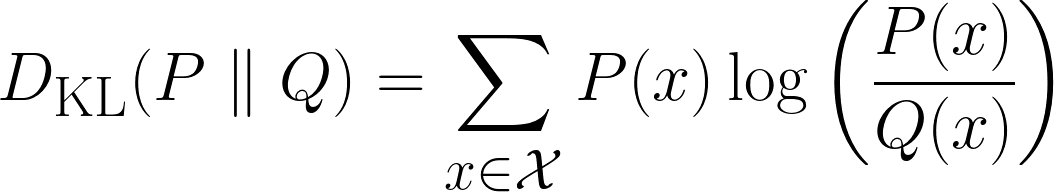
Y sí, la pregunta que te harás es ¿por qué? 

Volvamos a la intuición de la sorpresa.

• La entropía nos indica la cantidad mínima de sorpresa posible si conociéramos la distribución real P(x). Piensa en ello como el «coste ideal».
• La entropía cruzada nos indica la cantidad real de sorpresa que experimentamos al utilizar la aproximación Q(x). Piensa en ello como el «coste real».

Por lo tanto, cuando calculamos la divergencia KL restando estas cantidades, nos preguntamos cuánta sorpresa adicional estamos pagando por haber utilizado la distribución incorrecta Q(x) en lugar de la real P(x). Es el castigo por tener creencias equivocadas.

También es importante tener en cuenta que si Q(x) es igual a P(x), entonces la divergencia KL será igual a 0. Esto tiene sentido: si las predicciones de nuestro modelo coinciden perfectamente con la distribución real, entoncesno hayninguna sorpresa adicional y, por lo tanto, no hay penalización.

Esto es diferente de la entropía cruzada, que no llega a cero ni siquiera cuando P(x) es igual a Q(x); simplemente es igual a la entropía de P(x).

Así que podemos pensar en KL-Divergence como «anclada» en cero, lo que significa que solo comienza a aumentar cuando nuestra distribución prevista comienza a divergir de la verdadera.

Ejemplos

¡Buen trabajo derivando la ecuación! Para consolidar nuestro concepto, veamos un ejemplo que lo ilustra. 

Imagina que tenemos la tarea de predecir el género de películas favorito de un usuario. A partir de datos anteriores, se nos ha proporcionado la distribución real de los cuatro géneros cinematográficos (es decir, este es nuestro P(x)).

Ahora, juntos, hemos construido un modelo que predijo esto (es decir, este es nuestro Q(x)).

Es evidente que hay alguna diferencia en nuestra distribución, pero ¿cuán grande es? Aquí es donde utilizaremos la divergencia KL, utilizando la siguiente ecuación:

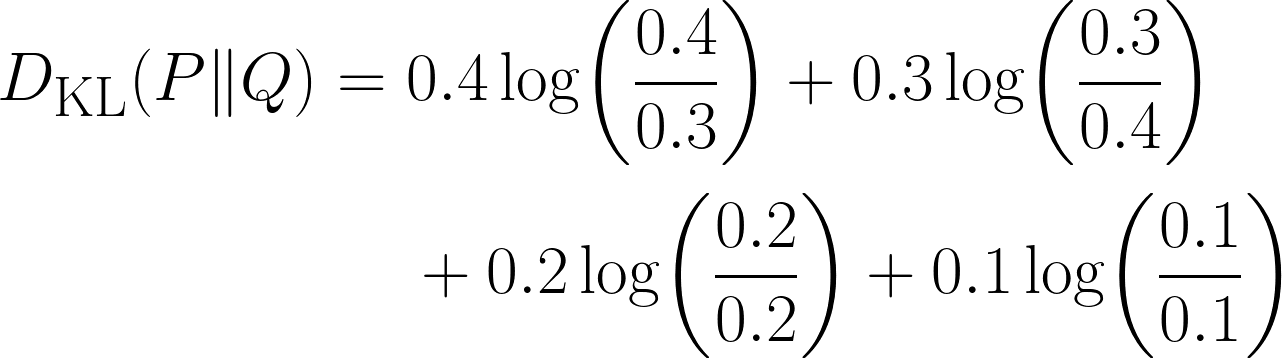
Observa cómo el término se convierte en 0 cuando las dos distribuciones tienen la misma probabilidad para ese resultado. 

Codificación

También podemos resolver el problema anterior utilizando Python:

import numpy as np
from scipy.stats import entropy      # Important module from scipy

P = np.array([0.4, 0.3, 0.2, 0.1])   # This is our true distribution
Q = np.array([0.3, 0.4, 0.2, 0.1])   # This is our model’s prediction

kl_nats = entropy(P, Q)              # natural log ⇒ nats
kl_bits = entropy(P, Q, base=2)      # log₂ ⇒ bits

print(f"KL(P‖Q) = {kl_nats} nats")
print(f"KL(P‖Q) = {kl_bits} bits")

Este código es bastante sencillo e intuitivo, aparte del hecho de que no hemos utilizado el término «divergencia KL» en ninguna parte del código. Más bien, he utilizadomuchas veces la entropía de un .

Esto nos lleva a un punto importante: la divergencia KL a menudo se denomina entropía relativa. Por lo tanto, estamos calculando la divergencia KL, ya que el módulo de entropía calcula la entropía relativa entre las dos distribuciones.

Esto parece confuso, así que quiero hacer una breve pausa y resumir todo:

Propiedades de la divergencia KL

Ahora que hemos calculado nuestro primer ejemplo utilizando la fórmula de la divergencia KL, dediquemos un momento a explorar algunas de sus propiedades más importantes.

1. No negatividad: La divergencia KL nunca es negativa. Esto tiene sentido intuitivamente, ya que el valor más bajo que puede tomar es 0, que es cuando nuestra distribución prevista es exactamente igual a la distribución real. Y nunca podemos tener un coste negativo, ya que no podemos estar «menos sorprendidos» que la sorpresa mínima teórica.
2. Anclado en cero: La divergencia KL nos da cero cuando nuestra distribución prevista coincide con la distribución real.
3. Unidades: Bits contra nats: Cuando calculamos la divergencia KL, utilizamos logaritmos. Pero la base de ese logaritmo determina la unidad del resultado final:

• Si utilizamos la base logarítmica 2, el resultado se mide en bits.
• Si utilizamos el logaritmo natural (ln), el resultado se mide en nats (abreviatura de «unidades naturales de información»).

4. Asimetría: Esta es una propiedad importante: la divergencia KL noes simétrica. Si utilizamos Q(x)para aproximar P(x), obtenemos un valor diferente al que obtenemos si utilizamos P(x) para aproximar Q(x). Por eso la KL-Divergence no es una medida de distancia real, ya que no se comporta como las distancias normales.

Aplicaciones de la divergencia KL en el machine learning

La divergencia KL es útil en muchas áreas diferentes del machine learning:

• Evaluación del modelo: medir la diferencia entre tus predicciones y las etiquetas reales.
• Inferencia variacional: minimizar DKL(q(z∣x)∥p(z∣x))D_{\text{KL}}(q(z|x) \| p(z|x))DKL​(q(z∣x)∥p(z∣x)) como en autocodificadores variacionales.
• Aprendizaje por refuerzo: La optimización de políticas de región de confianza (TRPO) utiliza restricciones KL.
• Modelado del lenguaje: comparación de predicciones de tokens con la verdad fundamental

Limitaciones de la divergencia KL y soluciones 

Como todo, el uso de la divergencia KL también tiene sus limitaciones. Explorémoslos en detalle:

1. El desajuste en el apoyo hace estallar KL: En casos excepcionales en los que Q(x)=0 y P(x)>0, el término fraccionario log(P/Q) se vuelve infinito. Para resolver esto, podemos añadir un suavizado ε o cambiar a la divergencia de Jensen-Shannon.
2. Características categóricas de alta cardinalidad: Tener múltiples valores daría lugar a recuentos dispersos y estimaciones KL ruidosas. Para solucionarlo, podemos fusionar categorías poco frecuentes o aplicar un suavizado bayesiano.
3. La asimetría puede ser bastante engañosa: Esto se debe a que KL(P || Q) y KL(Q || P) no producen el mismo valor. Una posible solución es utilizar la divergencia de Jensen-Shannon.
4. Unidades: Muchas veces, tendemos a olvidar incluir las unidades de KL-Divergence, y esto se vuelve especialmente problemático ya que tantolos nats como los bits se utilizan comúnmente. ¡Así que indica siempre la base del logaritmo!

divergencia de Jensen-Shannon

Quizás hayas notado que antes mencioné la divergencia de Jensen-Shannon, así que repasemos rápidamente de qué se trata. 

Aunque es ligeramente más complicada y requiere más cálculos que la divergencia KL, la divergencia de Jensen-Shannon es simétrica. Todavía no es una medida de distancia verdadera, ya que no cumple la desigualdad triangular. Sin embargo, si calculamos la raíz cuadrada de la divergencia JS, entonces sí cumple la desigualdad triangular y se convierte en una métrica adecuada. 

También es una versiónsuavizada de la divergencia KL que siempre se mantiene entre 0 y 1 bit (si utilizamos la base logarítmica 2). Si volvemos a mirar la ecuación, cada término KL se mide con respecto al punto medio compartido M, ni P ni Q se dividirán nunca por cero y, por lo tanto, no habrá infinitos. 

Conclusión

En resumen, la divergencia KL es una herramienta importante que utilizamos para medir el coste adicional de información que tenemos cuando dejamos que la distribución Q de nuestro modelo sustituya a la distribución real P. Es igual a cero si son iguales, mayor cuando no lo son y siempre no negativa. La divergencia KL conecta la entropía y la entropía cruzada, y aparece en funciones de pérdida, inferencia variacional y restricciones de políticas. 

Ahora bien, KL-Divergence es una herramienta excelente, pero sigue siendo una herramienta que utilizamos cuando nos enfrentamos a problemas relacionados con el machine learning y el deep learning. Para poder aplicar esto más adelante, no te pierdas nuestra programa Machine Learning Scientist in Python y nuestra programa de formación profesional de ingeniero de machine learning, donde se exploran tanto el aprendizaje supervisado como el no supervisado y el aprendizaje profundo.

Si también estás listo para empezar a relacionar la divergencia KL con otros conceptos matemáticos, echa un vistazo a estos recursos:

• Función de pérdida de entropía cruzada en machine learning: Mejora de la precisión del modelo: Aprende cómo se utiliza la entropía cruzada para optimizar la precisión de los modelos tanto en Pytorch como en Tensorflow.
• Desmitificando conceptos matemáticos para el aprendizaje profundo: Explora la cobertura completa de conceptos matemáticos importantes en el aprendizaje profundo, junto con código en Python.
• Comprender la deriva de datos y la deriva de modelos: Detección de desviaciones en Python: Descubre cómo se puede utilizar la divergencia KL para resolver un problema importante en el aprendizaje automático: la deriva del modelo.