Explicação sobre a divergência KL: Intuição, fórmula e exemplos

No machine learning, é super importante medir a precisão com que nossos modelos prevêem resultados do mundo real. Se você está criando um modelo de previsão do tempo ou otimizando um sistema de recomendações, precisa de uma maneira de quantificar o quanto suas previsões estão próximas da realidade. Uma maneira legal de fazer isso é usar a divergência KL.

Neste artigo, vou falar sobre o que é a divergência KL, por que ela é importante, como dá pra entender isso de um jeito intuitivo, os fundamentos matemáticos e exemplos práticos que mostram como ela funciona.

Se você está explorando conceitos de machine learning, recomendo fortemente que dê uma olhada no programa Fundamentos de machine learning em Python.

O que é a divergência KL?

A divergência KL (divergência de Kullback-Leibler) é uma medida estatística usada para ver como uma distribuição de probabilidade é diferente de outra distribuição de referência.

Vamos supor que estamos construindo um modelo juntos para prever o tempo de amanhã. Nos bastidores, nosso modelo tá fazendo apostas — atribuindo probabilidades a resultados possíveis. Mas tem uma pergunta importante pra gente fazer:

Como você mede o quão longe essas apostas estão da realidade? 

Precisamos de uma maneira de quantificar essa diferença, e é aí que entra a divergência KL. É uma ferramenta matemática que mostra a diferença entre o que nosso modelo acha e o que realmente é verdade.

Como eu disse antes, a divergência KL (ou mais formalmente conhecida como divergência de Kullback-Leibler) é a espinha dorsal da ciência de dados moderna, do machine learning e da IA. Isso nos diz, em bits ou nats (mais sobre isso depois), quanta “surpresa extra” ou “perda de informação” a gente tem quando usa uma distribuição de probabilidade (por exemplo, as previsões do nosso modelo, Q) para aproximar outra (a verdade do mundo real, P). 

Ele funciona como um juiz por trás da avaliação de modelos, regularização em redes neurais, atualizações bayesianas e até mesmo na forma como comprimimos dados ou transmitimos mensagens de maneira eficiente.

Para entender melhor a importância da divergência KL, pense nisso assim. Toda vez que nosso modelo faz uma previsão, é tipo apostar no futuro. KL-Divergence é o quadro de resultados que vai calcular quanto custam essas apostas. O mesmo vale pra vários assuntos de machine learning, tipo quando a gente tá treinando um chatbot, diagnosticando uma doença ou otimizando uma campanha de anúncios.

Matematicamente, a divergência KL é assim:

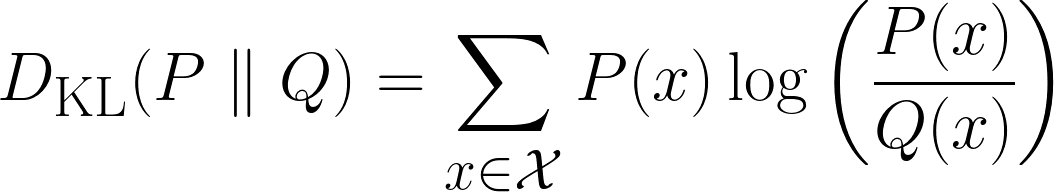
Acima está a fórmula para casos discretos e a fórmula abaixo é para casos contínuos.

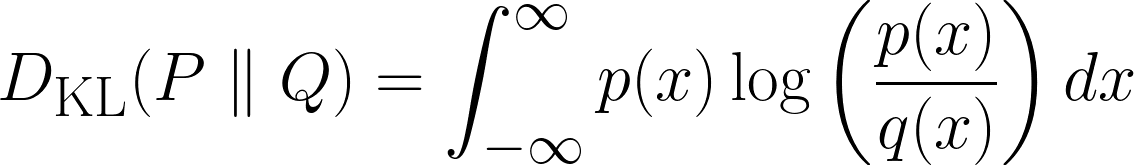
Intuição por trás da divergência KL

Nesta seção, vamos entender de forma intuitiva a divergência KL.  Vamos começar com umas perguntas.

Entendendo a surpresa

“Se você jogasse uma moeda e eu adivinhasse o resultado, você ficaria surpreso?”. Acho que você ficaria um pouco surpreso, mas não totalmente chocado. Agora, vamos passar para o segundo cenário.

Se você jogasse um dado e eu adivinhasse o resultado direitinho, você ficaria mais surpreso do que no cenário anterior? Acho que você diria que sim, já que é menos provável que eu adivinhe o resultado certo.

Agora, um último cenário:

Se eu tivesse adivinhado os números da loteria, você ficaria mais surpreso do que no cenário anterior? Acho que você diria que sim e ficaria completamente chocado. Mas por quê?

Isso porque, conforme a gente ia avançando nos cenários, a chance de eu adivinhar o resultado certo diminuía, e aí a sua surpresa com o resultado aumentava. Então, acabamos de perceber uma relação:

A chance de algo acontecer é inversamente proporcional à surpresa. 

Para ficar mais claro, quanto menor a chance de algo acontecer, maior a surpresa, e vice-versa. 

Mas dá pra fazer outra observação interessante aqui. Se voltarmos aos lançamentos dos dados e imaginarmos o cenário em que você lança os mesmos dados três vezes e eu acerto todas as vezes, você ficaria mais surpreso do que se houvesse apenas um dado e eu tivesse acertado? 

Bem, sua surpresa não seria só um pouco maior do que um único acerto; seria muito maior, idealmente três vezes maior. Por quê? Porque cada nova suposição correta aumenta sua descrença. Não é só adicionar uma dose fixa de surpresa — é multiplicar o quão inacreditável a situação parece.

Então, quando tentamos definir matematicamente a Surpresa, queremos que ela tenha:

1. Propriedade aditiva: Se dois eventos independentes rolam, a surpresa combinada deles deve ser a soma das surpresas individuais.
1. Exemplo: Adivinhar 1 lançamento de dado corretamente → Surpresa = S. Adivinhar 2 lançamentos de dado corretamente → Surpresa = S + S = 2S.
2. Relação inversa com a probabilidade. Quanto menos provável for um evento, mais surpreendente ele vai ser.
1. Exemplo: Jogar uma moeda ao ar (50%) é menos surpreendente do que ganhar na loteria (0,000001%).
3. Sem surpresas para certos eventos. Se algo sempre acontece (probabilidade = 1), a surpresa deve ser zero.
1. Exemplo: “O sol nasceu hoje.” → Não é nenhuma surpresa.
4. Escalonamento contínuo. Uma pequena mudança na probabilidade deve levar a uma mudança suave e lógica na surpresa (sem saltos repentinos).

À primeira vista, como tem muitos requisitos, a gente pode achar que a definição matemática vai ser bem complicada. Mas não é assim!

Todos os requisitos acima podem ser resolvidos usando a função logaritmo. A função logaritmo isolada (muitas vezes, log(x) e ln(x) são usados de forma intercambiável) tem a seguinte forma:

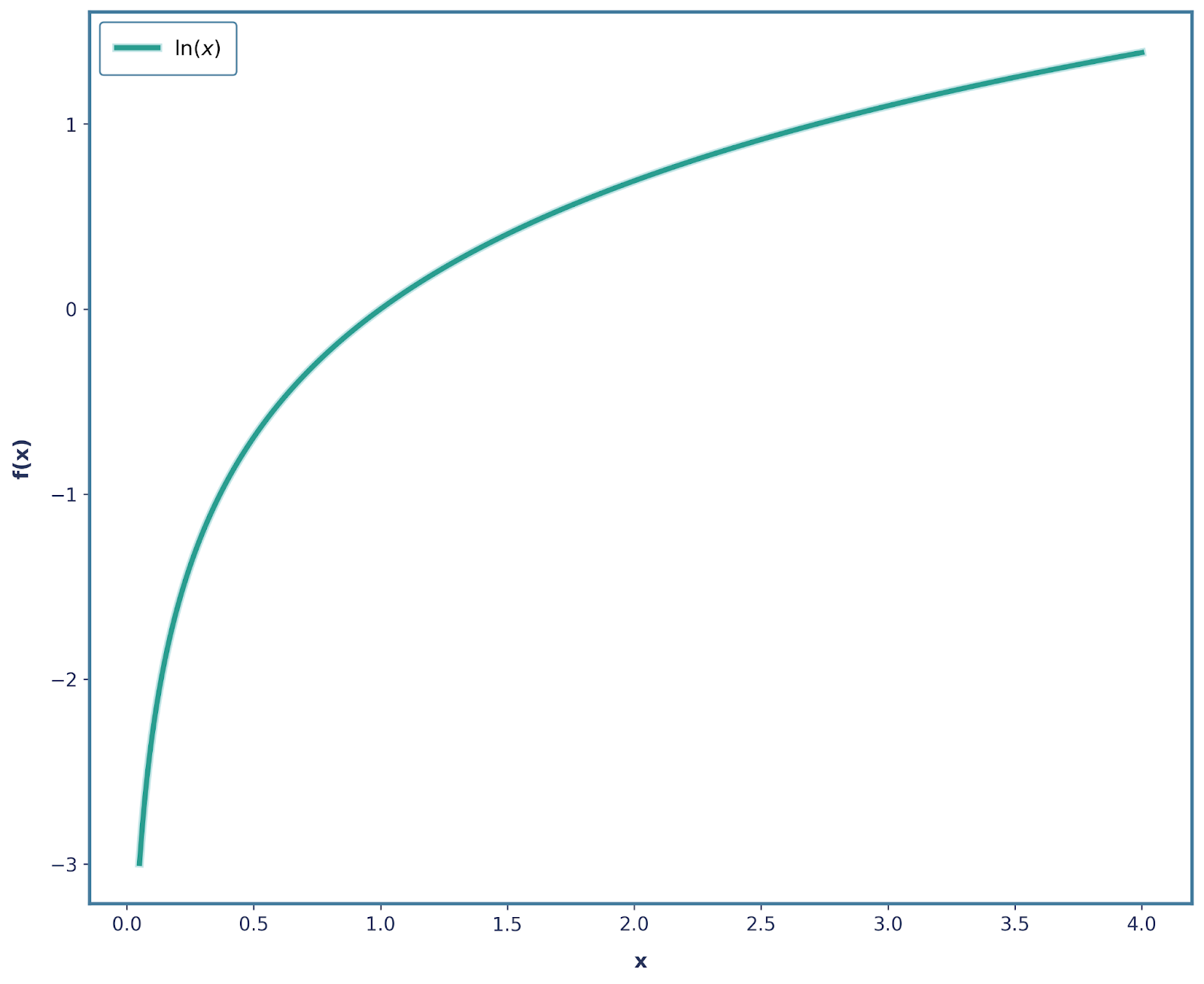
Já atendemos a boa parte dos nossos requisitos. Vamos focar primeiro napropriedade aditiva de . Lembra que a gente falou que, se dois eventos independentes rolam, a surpresa total deve ser a soma das surpresas individuais? Bem, é exatamente isso que a função log faz!

Veja como:

A chance de rolar um 6 em um dado justo é ⅙, e vamos definir a surpresa do evento assim:

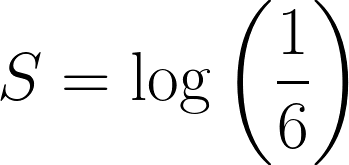
Agora, pense em jogar um dado três vezes seguidas e tirar um 6 , a probabilidade combinada seria: ⅙ * ⅙ * ⅙ = 1/216. 

Em termos de surpresa, seria:

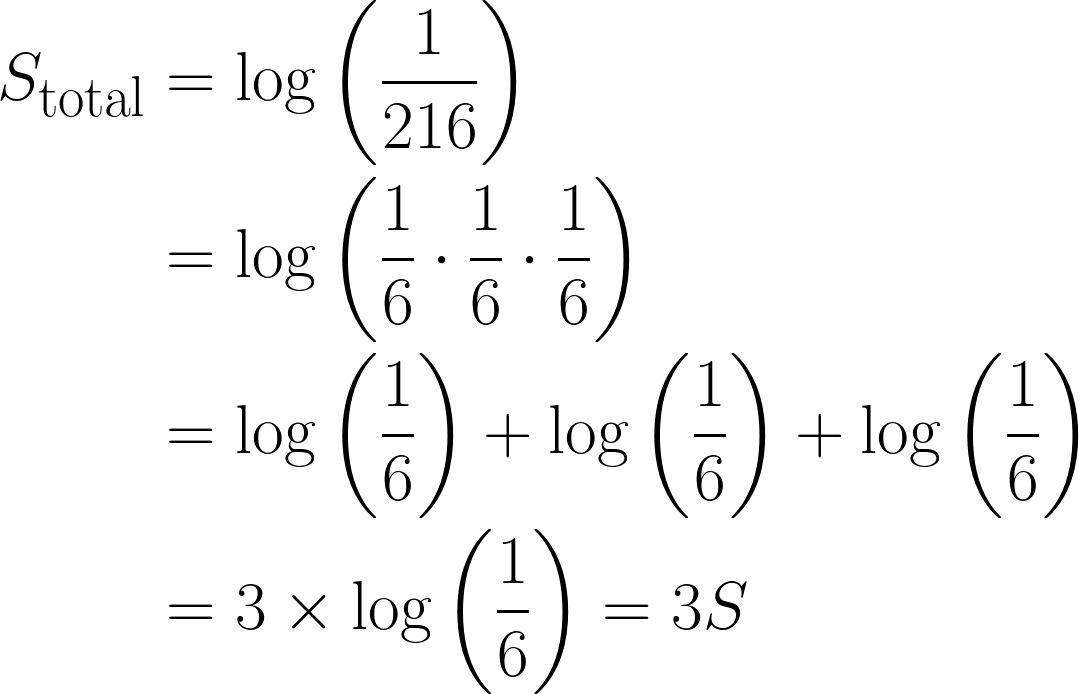
Essa é uma observação bem importante, já que a surpresa total aumentou em três vezes, por causa do logaritmo que usamos. Além disso, isso também satisfaz a Propriedade 3, onde log(1) = 0, já que um evento com certeza total não tem nenhum elemento de surpresa. 

Além disso, a Propriedade 4 também é satisfeita, pois log(x) é uma função monotônica contínua! Mas a Propriedade 2 não tá certa, porque nossa surpresa diminui quando a probabilidade diminui (já que ela fica mais negativa). 

Dá pra resolver isso fácil, colocando um sinal de menos! Então, nossa função agora é -log(x), que tem a forma abaixo. 

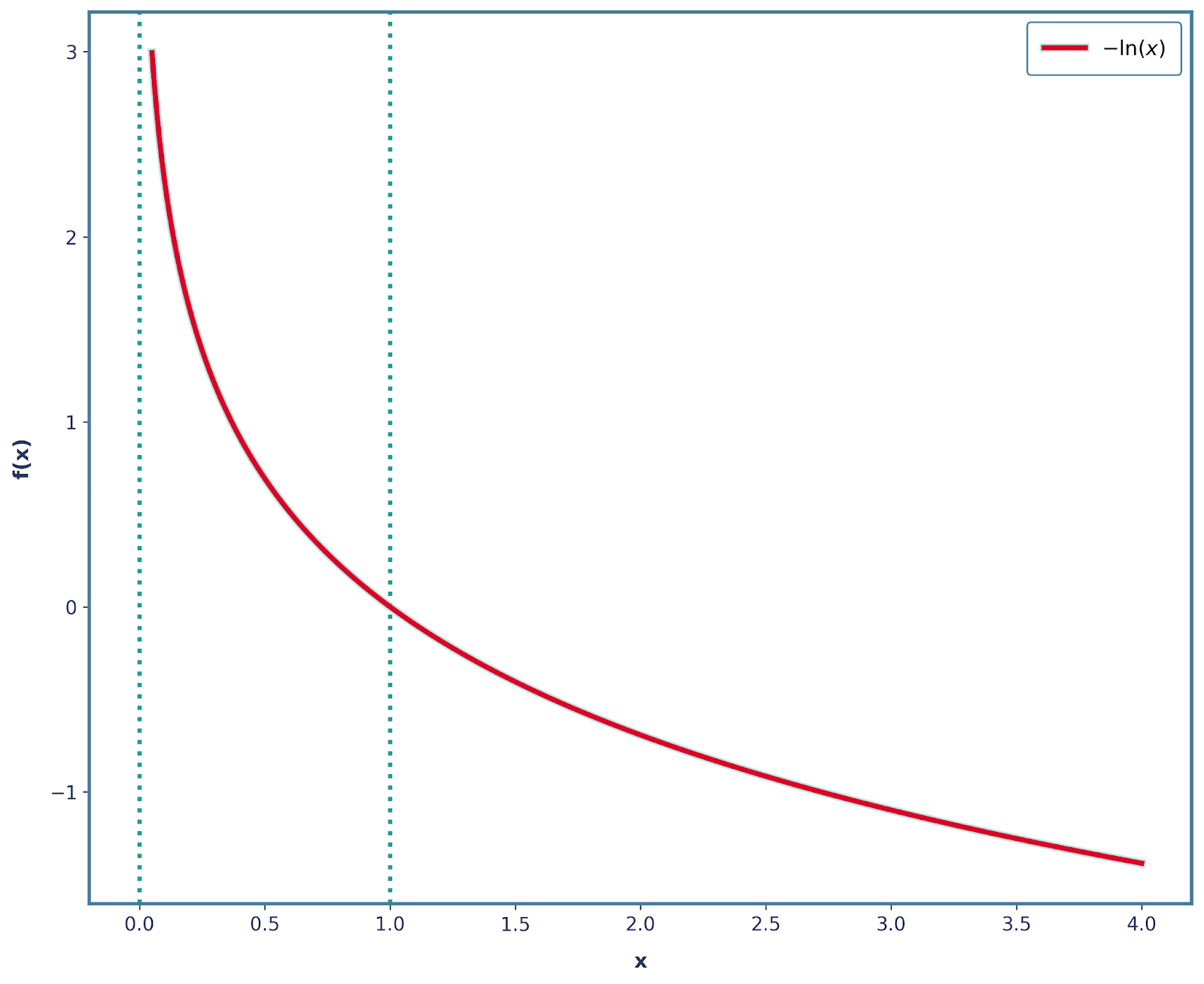
Também é importante notar que todas as outras 3 propriedades continuam a ser satisfeitas com esta alteração. Então, a gente pode definir matematicamente a surpresa como: 

Entropia

Em machine learning, não estamos interessados apenas na surpresa de um único evento, mas na surpresa média em todos os eventos possíveis. Isso é o que chamam de surpresa esperada. Mais especificamente, estamos interessados em descobrir a surpresa esperada da distribuição.

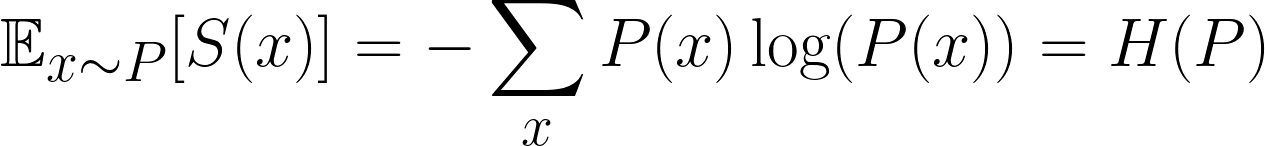
Essa é uma fórmula famosa e é a surpresa esperada, ou mais conhecida como Entropia. Mas, pra deixar tudo mais confuso, a gente costuma usar P e Q pra falar das nossas distribuições, então não confunda com p, que é pra provavelmente!

Intuitivamente falando, tudo o que estamos fazendo é multiplicar a probabilidade de cada resultado pela sua surpresae, em seguida, somando todos os resultados possíveis.

A partir daqui, vamos dizer que P(x) é a nossa distribuição subjacente real e Q(x)é a distribuição que estamos tentando aproximar de P(x)(ou seja, Q(X)é a distribuição “errada”). Isso é bem comum no machine learning — nossos modelos estão sempre tentando estimar o mundo real.

Então, agora vem a grande pergunta:

E se a gente calcular a nossa surpresa usando a distribuição errada?

Ainda podemos calcular a surpresa, mas em vez de usar P(x), agora a medimos em relação a Q(x). Isso nos dá uma nova expectativa:

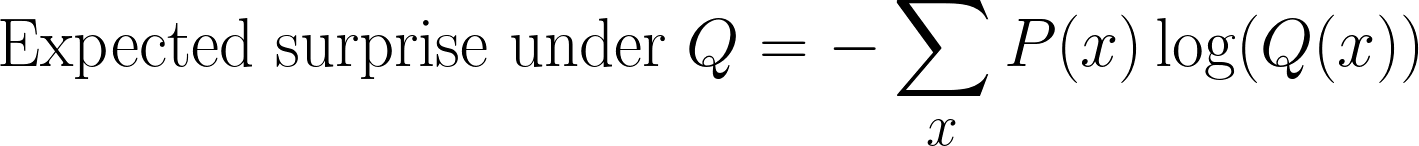
Esse é um passo que costuma ser confuso quando a gente está calculando a divergência KL. Ainda estamos fazendo amostragens de acordo com P(x) (porque essa é a distribuição real), mas estamos medindo a surpresa usando Q(x)(a crença do nosso modelo).

Essa quantidade às vezes é chamada de entropia cruzada entre P(x)e Q(x).

Fórmula da divergência KL

Até agora, a gente definiu duas coisas:

1. Entropia: a surpresa esperada se usarmos a distribuição real P(x)
2. Entropia cruzada: a surpresa esperada se usarmos o errada distribuição Q(x)

Para chegar na fórmula da divergência KL, é só tirar uma coisa da outra e pronto: 

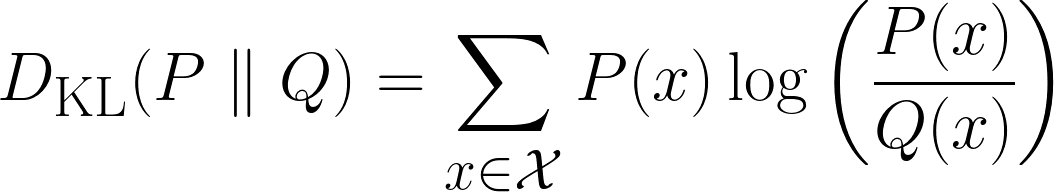
E sim, a pergunta que você vai fazer é: por quê? 

Vamos voltar à intuição da surpresa.

• A entropia nos diz a quantidade mínima de surpresa possível se soubéssemos a verdadeira distribuição P(x). Pense nisso como o “custo ideal”.
• A entropia cruzada mostra a quantidade real de surpresa que a gente tem ao usar a aproximação Q(x). Pense nisso como o “custo real”.

Então, quando calculamos a divergência KL subtraindo essas quantidades, estamos perguntando quanto a mais estamos pagando por usar a distribuição errada Q(x) em vez da verdadeira P(x). É o preço que se paga por ter as crenças erradas.

Uma coisa importante a se notar é que, se Q(x) for igual a P(x), então a divergência KL vai ser igual a 0. Isso faz sentido — se as previsões do nosso modelo batem com a distribuição real,não temnenhuma surpresa extra e, portanto, nenhuma penalidade.

Isso é diferente da entropia cruzada, que não chega a zero mesmo quando P(x) é igual a Q(x); ela é igual à entropia de P(x).

Então, a gente pode pensar na KL-Divergence como sendo “ancorado” em zero, o que significa que só começa a aumentar quando nossa distribuição prevista começa a divergir da verdadeira.

Exemplos

Boa em chegar à equação! Para entender melhor, vamos ver um exemplo. 

Imagina que a gente tem que adivinhar qual é o gênero de filme favorito de um usuário. Com base em dados anteriores, obtivemos a distribuição real dos quatro gêneros de filmes (ou seja, este é o nossoP(x) ).

Agora, juntos, criamos um modelo que previu isso (ou seja, este é o nosso Q(x)).

Tem uma diferença clara na nossa distribuição, mas qual é a diferença? É aqui que vamos usar a divergência KL, com a equação abaixo:

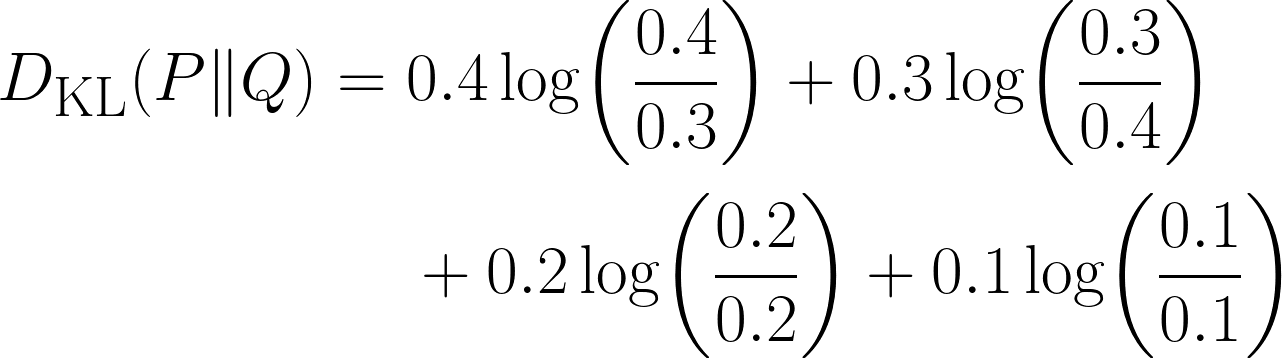
Repara como o termo fica 0 quando as duas distribuições têm a mesma probabilidade para esse resultado. 

Codificação

Também podemos resolver o problema acima usando Python:

import numpy as np
from scipy.stats import entropy      # Important module from scipy

P = np.array([0.4, 0.3, 0.2, 0.1])   # This is our true distribution
Q = np.array([0.3, 0.4, 0.2, 0.1])   # This is our model’s prediction

kl_nats = entropy(P, Q)              # natural log ⇒ nats
kl_bits = entropy(P, Q, base=2)      # log₂ ⇒ bits

print(f"KL(P‖Q) = {kl_nats} nats")
print(f"KL(P‖Q) = {kl_bits} bits")

Esse código é bem simples e intuitivo, tirando o fato de que não usamos o termo KL-Divergence em nenhum lugar do código! Em vez disso, useimuitas vezes a entropia .

Isso nos leva a um ponto importante - KL-Divergence é frequentemente chamada de Entropia Relativa. Então, a gente tá calculando a divergência KL, já que o módulo de entropia tá calculando a entropia relativa entre as duas distribuições.

Isso parece meio confuso, então vou dar uma pausa e resumir tudo:

Propriedades da divergência KL

Agora que já calculamos nosso primeiro exemplo usando a fórmula da divergência KL, vamos dar uma olhada em algumas das propriedades mais importantes dela.

1. Não negatividade: A divergência KL nunca é negativa. Isso faz sentido intuitivamente, já que o menor valor que pode ter é 0, que é quando a nossa distribuição prevista é exatamente igual à distribuição real. E nunca podemos ter um custo negativo, já que não podemos ficar “menos surpresos” do que a surpresa mínima teórica.
2. Ancorado no zero: A divergência KL dá zero quando a distribuição que a gente espera bate com a distribuição real.
3. Unidades: Bits vs nats: Quando calculamos a divergência KL, usamos logaritmos. Mas a base desse logaritmo é que decide a unidade do resultado final:

• Se usarmos a base log 2, o resultado é medido em bits.
• Se usarmos o logaritmo natural (ln), o resultado é medido em nats (abreviação de “unidades naturais de informação”).

4. Assimetria: Essa é uma propriedade importante - a divergência KL nãoé simétrica. Usarum Q(x) d para aproximar P(x) dá um valor diferente do que usar P(x) para aproximar Q(x). É por isso que a divergência KL ( ) não é uma medida de distância de verdade — ela não funciona como as distâncias normais.

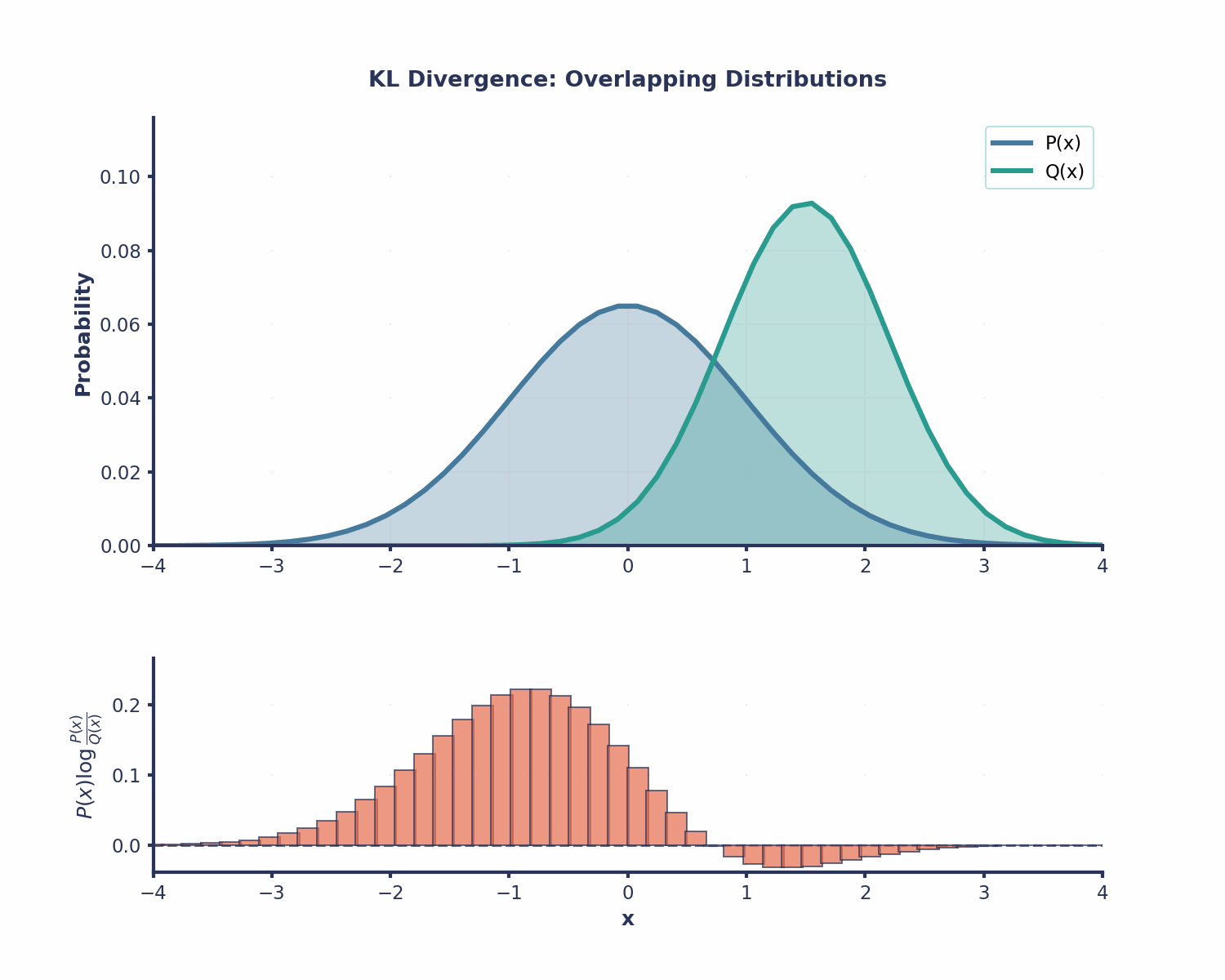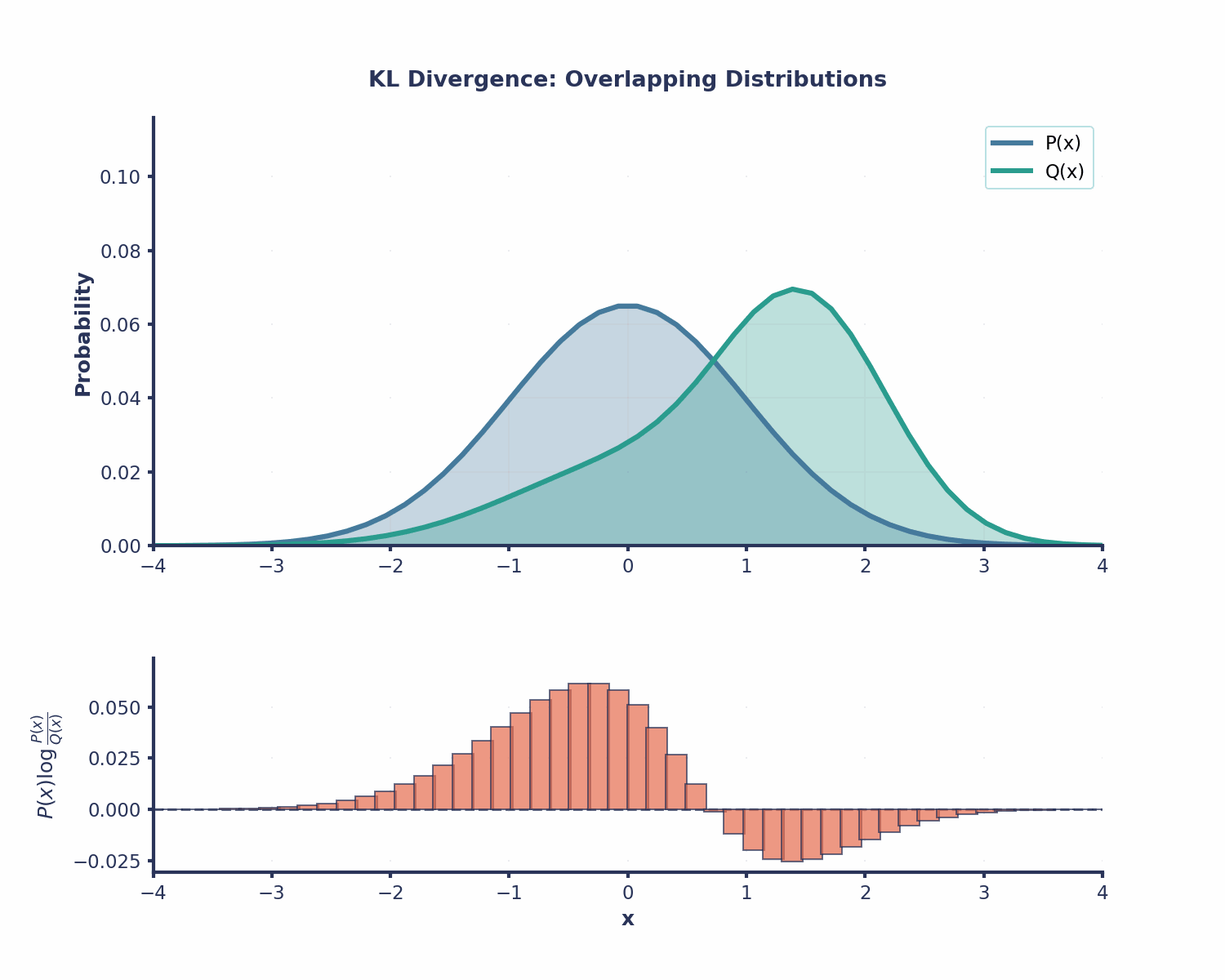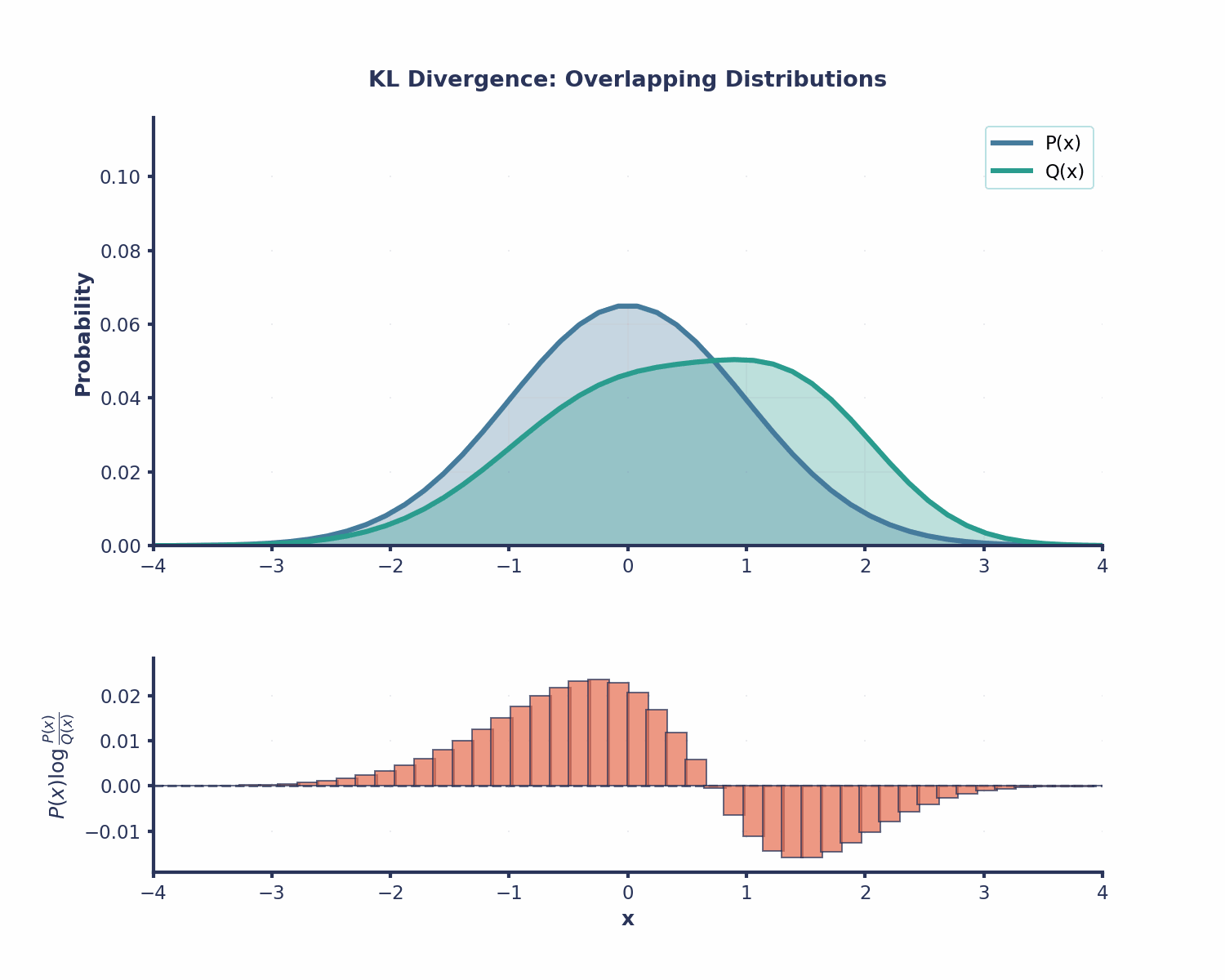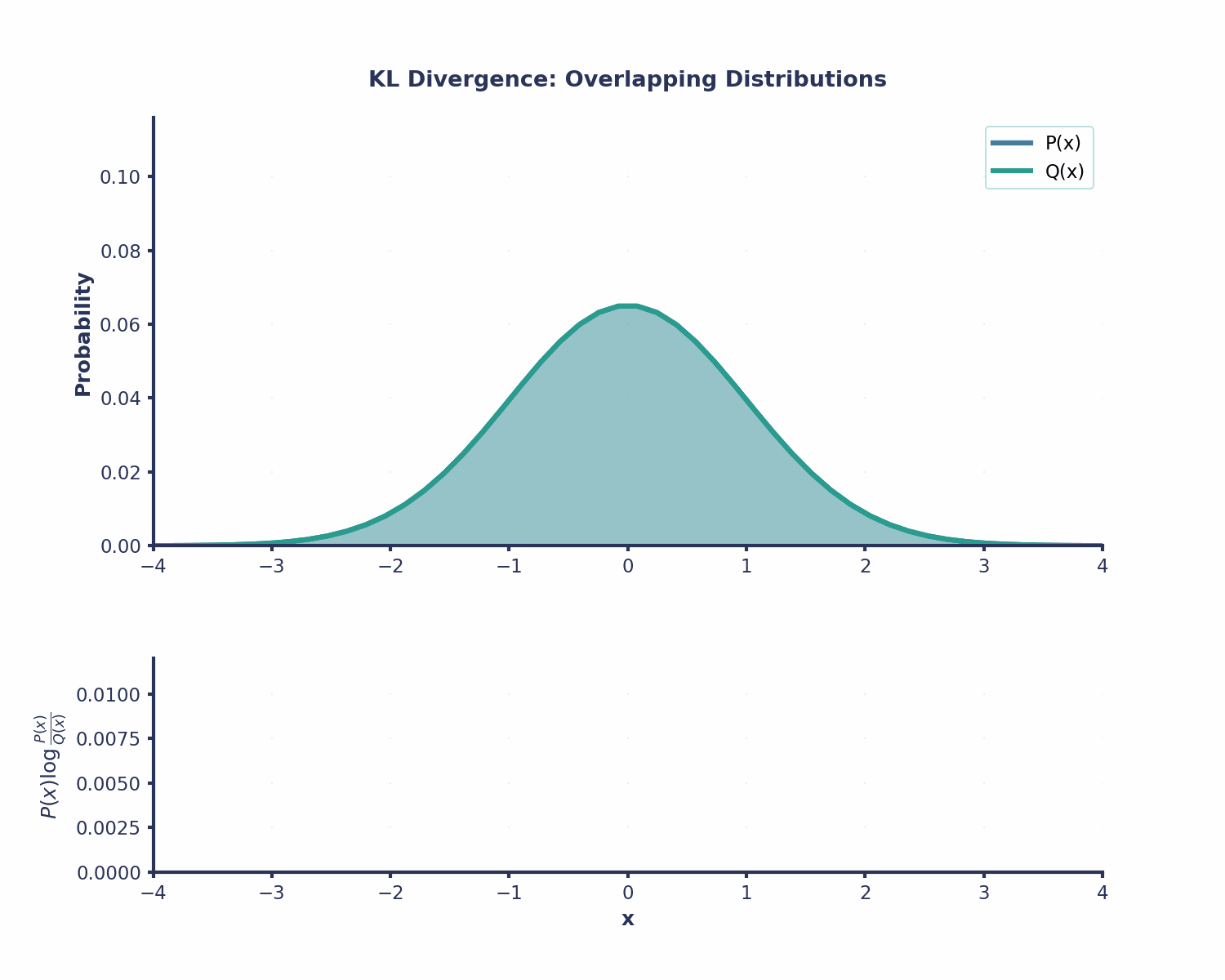
Aplicações da divergência KL no machine learning

A divergência KL é útil em várias áreas do machine learning:

• Avaliação do modelo: medindo o quanto suas previsões estão longe dos rótulos reais
• Inferência variacional: minimizando DKL(q(z∣x)∥p(z∣x))D_{\text{KL}}(q(z|x) \| p(z|x))DKL​(q(z∣x)∥p(z∣x)), como em Autoencoders Variacionais.
• Aprendizagem por reforço: A Otimização da Política de Região de Confiança (TRPO) usa restrições KL.
• Modelagem de linguagem: comparando previsões de tokens com a verdade fundamental

Limitações da divergência KL e soluções 

Como tudo na vida, também tem umas limitações no uso da divergência KL. Vamos ver isso de um jeito mais detalhado:

1. Incompatibilidade de suporte explode KL: Em casos raros em que Q(x)=0 e P(x)>0, o termo fracionário log(P/Q) torna-se infinito. Para resolver isso, podemos adicionar o suavização ε ou mudar para a divergência de Jensen-Shannon.
2. Características categóricas de alta cardinalidade: Ter vários valores levaria a contagens esparsas e estimativas KL ruidosas. Para resolver isso, podemos juntar categorias raras ou usar o alisamento bayesiano.
3. A assimetria pode ser bem enganadora: Isso é porque KL(P || Q) e KL(Q || P) não dão o mesmo resultado. Uma possível solução é usar a divergência de Jensen-Shannon.
4. Unidades: Muitas vezes, a gente esquece de incluir as unidades de divergência KL, e isso é um problema, porque tantoos nats ( ) quanto os bits ( ) são usados com frequência. Portanto, sempre diga qual é a base do logaritmo!

Divergência de Jensen-Shannon

Você deve ter notado que eu já falei sobre a Divergência de Jensen-Shannon antes, então vamos dar uma olhada rápida nisso. 

Embora seja um pouco mais complicado e mais pesado em termos computacionais do que a divergência KL, a divergência Jensen-Shannon é simétrica. Ainda não é uma medida de distância de verdade, porque não cumpre a desigualdade triangular. Mas, se a gente tirar a raiz quadrada da JS-Divergence, ela passa a satisfazer a desigualdade triangular e vira uma métrica legal. 

É também uma versãosuavizada da divergência KL, que sempre fica entre 0 e 1 bit (se usarmos log base 2). Se olharmos novamente para a equação, cada termo KL é medido em relação ao ponto médio compartilhado M, nem P nem Q serão nunca divididos por zero e, portanto, não haverá infinitos. 

Conclusão

Resumindo, a divergência KL é uma ferramenta importante que usamos pra medir o custo extra de informação que temos quando deixamos a distribuição Q do nosso modelo substituir a distribuição real P. Ela fica zero se elas forem iguais e maior quando não forem, e sempre não negativa. A divergência KL conecta entropia e entropia cruzada e aparece em funções de perda, inferência variacional e restrições de política. 

Agora, a KL-Divergence é ótima, mas ainda é uma ferramenta que usamos quando lidamos com problemas relacionados a Machine Learning e Deep Learning. Para poder aplicar isso mais adiante, não deixe de conferir nossa programa de carreira Cientista de Machine Learning em Python e nossa programa de carreira de Engenheiro de Machine Learning, que falam sobre aprendizado supervisionado, não supervisionado e profundo.

Se você também está pronto para começar a conectar a divergência KL com outros conceitos matemáticos, dê uma olhada nesses recursos:

• Função de perda de entropia cruzada em machine learning: Melhorando a precisão do modelo: Aprenda como a entropia cruzada é usada pra otimizar a precisão do modelo tanto no Pytorch quanto no Tensorflow.
• Desmistificando conceitos matemáticos para o aprendizado profundo: Explore a cobertura completa de conceitos matemáticos importantes em Deep Learning, junto com código em Python.
• Entendendo a deriva de dados e a deriva de modelos: Detecção de desvio no Python: Descubra como a divergência KL pode ser usada pra resolver um problema importante em ML: a deriva do modelo.