Cross-Entropy Loss Function in Machine Learning: Verbesserung der Modellgenauigkeit

Entropie verstehen

Das Konzept der Kreuzentropie geht auf die Informationstheorie zurück, in der die Informationsentropie, auch bekannt als Shannon-Entropie, 1948 von Claude Shannon in einem Aufsatz mit dem Titel "A Mathematical Theory of Communication" formell eingeführt wurde. Bevor wir uns mit der Kreuzentropie befassen, wollen wir uns mit der Entropie beschäftigen.

Die Entropie berechnet den Grad der Zufälligkeit oder Unordnung in einem System. Im Kontext der Informationstheorie ist die Entropie einer Zufallsvariablen die durchschnittliche Unsicherheit, Überraschung oder Information, die den möglichen Ergebnissen innewohnt. Vereinfacht gesagt, misst sie die Unsicherheit eines Ereignisses.

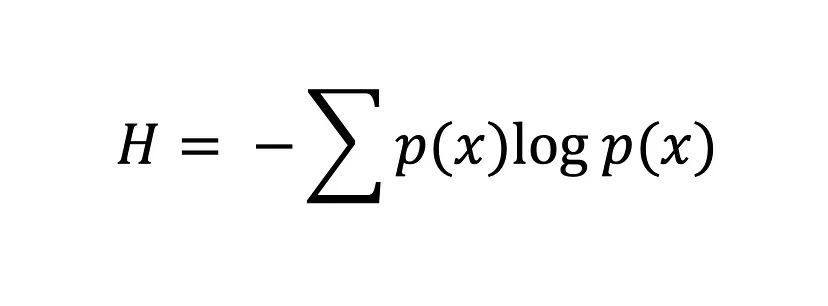
Die Shannon-Entropie-Gleichung

Je größer der Wert der Entropie H(x) ist, desto größer ist die Unsicherheit der Wahrscheinlichkeitsverteilung, und je kleiner der Wert, desto geringer ist die Unsicherheit.

Was ist Cross-Entropie?

Die Kreuzentropie, auch bekannt als logarithmischer Verlust oder Log-Verlust, ist eine beliebte Verlustfunktion, die beim maschinellen Lernen verwendet wird, um die Leistung eines Klassifikationsmodells zu messen.

Sie misst die durchschnittliche Anzahl von Bits, die benötigt wird, um ein Ereignis aus einer Wahrscheinlichkeitsverteilung p mit dem optimalen Code für eine andere Wahrscheinlichkeitsverteilung q zu identifizieren. Mit anderen Worten: Die Kreuzentropie misst die Differenz zwischen der ermittelten Wahrscheinlichkeitsverteilung eines Klassifikationsmodells und den vorhergesagten Werten.

Die Cross-Entropie-Verlustfunktion wird verwendet, um die optimale Lösung zu finden, indem die Gewichte eines maschinellen Lernmodells während des Trainings angepasst werden. Das Ziel ist es, den Fehler zwischen dem tatsächlichen und dem vorhergesagten Ergebnis zu minimieren. Ein niedrigerer Wert der Kreuzentropie bedeutet eine bessere Leistung. 

Wenn du mit der Kullback-Leibler (KL)-Divergenz vertraut bist, fragst du dich vielleicht: "Was ist der Unterschied zwischen Kreuzentropie und KL-Divergenz?" Und das ist eine berechtigte Frage. Beide Konzepte werden häufig verwendet, um Unterschiede oder Ähnlichkeiten von Wahrscheinlichkeitsverteilungen zu messen. Obwohl sie einige Gemeinsamkeiten haben, dienen sie unterschiedlichen Zwecken.

Wie bereits erwähnt, misst die Kreuzentropie die durchschnittliche Anzahl von Bits, die erforderlich ist, um ein Ereignis aus einer Wahrscheinlichkeitsverteilung (P) mit dem optimalen Code für eine andere Wahrscheinlichkeitsverteilung (Q) zu identifizieren, und wird in der Regel beim maschinellen Lernen verwendet, um die Leistung eines Modells zu bewerten, bei dem das Ziel darin besteht, den Fehler zwischen der vorhergesagten Wahrscheinlichkeitsverteilung und der wahren Verteilung zu minimieren.

Im Gegensatz dazu misst die KL-Divergenz die Differenz zwischen zwei Wahrscheinlichkeitsverteilungen, P und Q. Die KL-Divergenz quantifiziert den Informationsverlust, der entsteht, wenn Q zur Annäherung an P verwendet wird. Dies ist unglaublich nützlich bei unüberwachten Lernaufgaben, bei denen es darum geht, Strukturen in den Daten aufzudecken, indem die Divergenz zwischen der wahren und der gelernten Datenverteilung minimiert wird.

Kreuzentropie als Verlustfunktion

Beim maschinellen Lernen helfen Verlustfunktionen den Modellen dabei, festzustellen, wie falsch sie liegen, und sich auf dieser Grundlage zu verbessern. Sie sind mathematische Funktionen, die den Unterschied zwischen vorhergesagten und tatsächlichen Werten in einem maschinellen Lernmodell quantifizieren, aber das ist nicht alles, was sie tun.

Das Fehlermaß einer Verlustfunktion dient auch als Orientierungshilfe während des Optimierungsprozesses, indem es dem Modell Rückmeldung darüber gibt, wie gut es zu den Daten passt. Daher implementieren die meisten maschinellen Lernmodelle während der Optimierungsphase eine Verlustfunktion, bei der die Modellparameter so gewählt werden, dass das Modell den Fehler minimiert und zu einer optimalen Lösung gelangt - je kleiner der Fehler, desto besser das Modell.

Wir können den Fehler zwischen zwei Wahrscheinlichkeitsverteilungen mithilfe der Cross-Entropie-Verlustfunktion messen. Nehmen wir zum Beispiel an, wir führen eine binäre Klassifizierungsaufgabe durch (eine Klassifizierungsaufgabe mit zwei Klassen, 0 und 1).

In diesem Fall müssen wir die binäre Kreuzentropie verwenden, die die durchschnittliche Kreuzentropie über alle Datenproben hinweg ist:

Binäre Kreuzentropieformel [Quelle: Cross-Entropy Loss Function]

Wenn wir den Verlust eines einzelnen Datenpunktes berechnen würden, bei dem der richtige Wert y=1 ist, würde unsere Gleichung folgendermaßen aussehen:

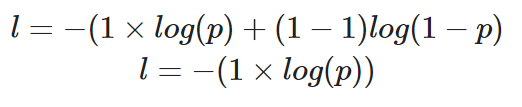
Berechnung der binären Kreuzentropie für eine einzelne Instanz, bei der der wahre Wert 1 ist

Die vorhergesagte Wahrscheinlichkeit, p, bestimmt den Wert des Verlustes, l. Wenn der Wert von p hoch ist, wird das Modell für eine korrekte Vorhersage belohnt - dies wird durch einen niedrigen Wert des Verlusts l dargestellt.

Eine niedrige Vorhersagewahrscheinlichkeit p würde jedoch darauf hindeuten, dass das Modell falsch ist, und die binäre Kreuzentropie-Verlustfunktion spiegelt dies wider, indem sie den Wert von l erhöht.

Für eine Mehrklassen-Klassifizierungsaufgabe kann die Cross-Entropie (oder kategoriale Cross-Entropie, wie sie oft genannt wird) einfach wie folgt erweitert werden:

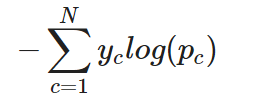
Kategoriale Kreuzentropie für eine einzelne Instanz

Mit anderen Worten: Um die Cross-Entropie auf eine Klassifizierungsaufgabe mit mehreren Klassen anzuwenden, wird der Verlust für jede Klasse separat berechnet und dann summiert, um den Gesamtverlust zu ermitteln.

Implementierung von Cross-Entropy Loss in PyTorch und TensorFlow

In diesem Teil des Tutorials lernen wir, wie man die Cross-Entropie-Verlustfunktion in TensorFlow und PyTorch verwendet.

Beginnen wir mit der Erstellung des Datensatzes. Wir werden die Funktion make_classification von Scikit nutzen, um uns zu helfen:

from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split

 # create training data
X, y = make_classification(
    n_samples=10000,
    n_informative=10,
    random_state=2022
)

# split into train and test
X_new, X_test = X[:9000, :], X[9000:, ]
y_new, y_test = y[:9000], y[9000:]

X_train, X_val, y_train, y_val = train_test_split(
    X_new, y_new,
    test_size=0.3
)
print(f"Train data: {X_train.shape}\n\
Train labels: {y_train.shape}\n\
Test data: {X_test.shape}\n\
Test labels: {y_test.shape}")

"""
Train data: (6300, 20)
Train labels: (6300,)
Test data: (1000, 20)
Test labels: (1000,)
"""

Kreuzentropie in TensorFlow

Das Modell, das wir erstellen werden, besteht aus einer Eingabeschicht, einer verborgenen Schicht und einer Ausgabeschicht.

Da es sich um eine binäre Klassifizierungsaufgabe handelt, werden wir die binäre Kreuzentropie als Verlustfunktion verwenden.

# building and training model
model = tf.keras.Sequential([
                            tf.keras.layers.Dense(10,
                                                  input_shape=(X_train.shape[1],),
                                                  activation="relu"),
                            tf.keras.layers.Dense(10,
                                                  activation="relu"),
                            tf.keras.layers.Dense(1, activation="sigmoid")
])

model.compile(
    loss="binary_crossentropy", # loss function here
    optimizer="adam",
    metrics=["accuracy"])

history = model.fit(X_train, y_train, epochs=20, validation_data=[X_val, y_val], verbose=0)

Als Nächstes werden wir den Verlust aufzeichnen, um zu sehen, ob sich das Modell verbessert - das heißt, der Fehler nimmt mit jeder Epoche ab, bis es sich nicht mehr verbessern kann.

# plotting the loss of the models
fig, ax = plt.subplots(figsize=(8,5))
plt.plot(history.history['loss'])
plt.plot(history.history['val_loss'])
plt.title('model loss')
plt.ylabel('loss')
plt.xlabel('epoch')
plt.xticks(np.arange(0,20, step=1))
plt.legend(['train', 'test'], loc='upper right')
plt.show()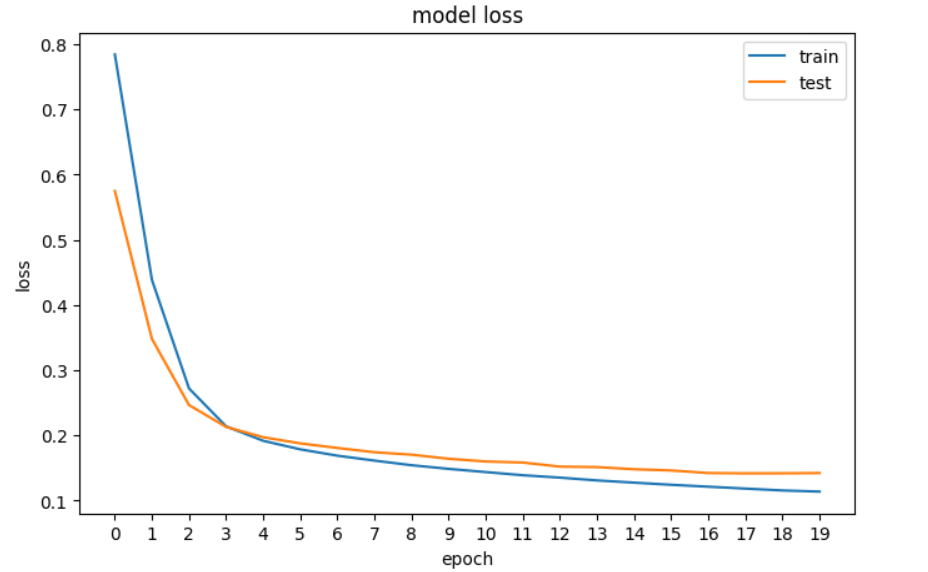

Eine Darstellung des Verlusts unseres neuronalen Netzes in TensorFlow.

Kreuzentropie in PyTorch

In PyTorch werden die Eingaben, Ausgaben und Parameter des Modells mit Tensoren kodiert, was bedeutet, dass wir unsere Numpy-Arrays in Tensoren umwandeln müssen. Das ist das erste, was wir im folgenden Code tun. Dann bauen wir das neuronale Netz auf und geben seine Dimensionen aus.

# convert numpy arrays to tensors 
X_train_tensor = torch.tensor(X_train, dtype=torch.float32)
X_val_tensor = torch.tensor(X_val, dtype=torch.float32)
y_train_tensor = torch.tensor(y_train, dtype=torch.float32).reshape(-1, 1)
y_val_tensor = torch.tensor(y_val, dtype=torch.float32).reshape(-1, 1)

# build the model
input_dim = X_train.shape[1]
hidden_dim = 10
output_dim = 1

model = nn.Sequential(
    nn.Linear(input_dim, hidden_dim),
    nn.ReLU(),
    nn.Linear(hidden_dim, hidden_dim),
    nn.ReLU(),
    nn.Linear(hidden_dim, output_dim),
    nn.Sigmoid()
    )

print(model)

"""
Sequential(
  (0): Linear(in_features=20, out_features=10, bias=True)
  (1): ReLU()
  (2): Linear(in_features=10, out_features=10, bias=True)
  (3): ReLU()
  (4): Linear(in_features=10, out_features=1, bias=True)
  (5): Sigmoid()
)
"""

Als Nächstes definieren wir die binäre Cross-Entropy-Verlustfunktion und den Optimierer:

loss_fn = nn.BCELoss()  # binary cross entropy
optimizer = optim.Adam(model.parameters(), lr=0.001)

Und nun zum Planen des Verlustes:

# plotting the loss of the models
fig, ax = plt.subplots(figsize=(8,5))
plt.plot(train_loss)
plt.plot(val_loss)
plt.title('model loss')
plt.ylabel('loss')
plt.xlabel('epoch')
plt.xticks(np.arange(0,20, step=1))
plt.legend(['train', 'test'], loc='upper right')
plt.show()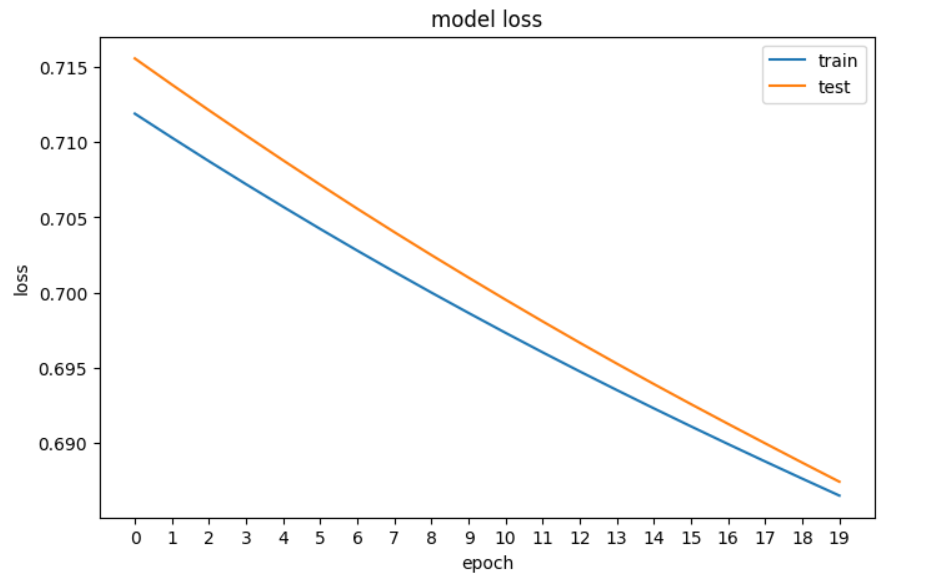

Eine Darstellung des Verlusts unseres neuronalen Netzes in PyTorch

Die wichtigsten Erkenntnisse

Hier ist eine kurze Zusammenfassung dessen, was wir über den Cross-Entropie-Verlust gelernt haben:

• Die Entropie berechnet den Grad der Zufälligkeit oder Unordnung innerhalb eines Systems, um die Unsicherheit eines Ereignisses zu messen. Wenn ein Ergebnis sicher ist, ist das Maß der Entropie niedrig.
• Die Kreuzentropie ist eine beliebte Verlustfunktion, die beim maschinellen Lernen verwendet wird, um die Leistung eines Klassifikationsmodells zu messen. Sie misst die Differenz zwischen der ermittelten Wahrscheinlichkeitsverteilung eines Klassifikationsmodells und den vorhergesagten Werten. Bei der Anwendung auf binäre Klassifizierungsaufgaben wird er üblicherweise als Log Loss bezeichnet.
• Die binäre Kreuzentropie wird für die binäre Klassifizierung verwendet, während die kategoriale Kreuzentropie für die Mehrklassen-Klassifizierung genutzt wird.
• Die Kreuzentropie ähnelt der KL-Divergenz, aber sie dienen unterschiedlichen Zwecken: Die Kreuzentropie wird typischerweise beim maschinellen Lernen verwendet, um die Leistung eines Modells zu bewerten, bei dem das Ziel darin besteht, den Fehler zwischen der vorhergesagten Wahrscheinlichkeitsverteilung und der wahren Verteilung zu minimieren, während die KL-Divergenz eher bei unüberwachten Lernaufgaben nützlich ist, bei denen das Ziel darin besteht, die Struktur in den Daten aufzudecken, indem die Divergenz zwischen der wahren und der gelernten Datenverteilung minimiert wird.

Um weiter zu lernen, schau dir unsere Ressourcen an:

• Neuronale Netzmodelle (NN) in R erstellen
• Einführung in Deep Learning in Python