Verlustfunktionen beim maschinellen Lernen erklärt

Verlustfunktionen in Kürze

Die wichtigste Erkenntnis ist, dass die Verlustfunktion eine messbare Methode ist, um die Leistung und Genauigkeit eines maschinellen Lernmodells zu messen. In diesem Fall dient die Verlustfunktion als Leitfaden für den Lernprozess innerhalb eines Modells oder maschinellen Lernalgorithmus.

Die Rolle der Verlustfunktion ist entscheidend für das Training von maschinellen Lernmodellen und umfasst Folgendes:

• Leistungsmessung: Verlustfunktionen bieten ein klares Maß zur Bewertung der Leistung eines Modells, indem sie den Unterschied zwischen Vorhersagen und tatsächlichen Ergebnissen quantifizieren.
• Richtung für Verbesserungen: Verlustfunktionen steuern die Modellverbesserung, indem sie den Algorithmus anweisen, die Parameter (Gewichte) iterativ anzupassen, um den Verlust zu verringern und die Vorhersagen zu verbessern.
• Ausgleich von Verzerrung und Varianz: Effektive Verlustfunktionen helfen dabei, Modellverzerrungen (Übervereinfachung) und Varianz (Überanpassung) auszugleichen, was für die Generalisierung des Modells auf neue Daten wichtig ist.
• Beeinflussung des Modellverhaltens: Bestimmte Verlustfunktionen können das Verhalten des Modells beeinflussen, z. B. indem sie robuster gegenüber Datenausreißern sind oder bestimmte Fehlertypen bevorzugen.

In den folgenden Abschnitten werden wir die Rolle der einzelnen Verlustfunktionen untersuchen und ein detailliertes Verständnis der Verlustfunktion entwickeln.

Was ist eine Verlustfunktion?

Die Verlustfunktion, die auch als Fehlerfunktion bezeichnet wird, ist eine entscheidende Komponente beim maschinellen Lernen, die den Unterschied zwischen den vorhergesagten Ausgaben eines maschinellen Lernalgorithmus und den tatsächlichen Zielwerten quantifiziert. Bei einem Regressionsproblem zur Vorhersage von Autopreisen auf der Grundlage historischer Daten bewertet eine Verlustfunktion die Vorhersage eines neuronalen Netzes auf der Grundlage einer Trainingsstichprobe aus dem Trainingsdatensatz. Die Verlustfunktion quantifiziert den Abstand bzw. die Fehlerspanne zwischen dem vom Netzwerk vorhergesagten und dem tatsächlichen Fahrzeugpreis.

Der daraus resultierende Wert, der Verlust, spiegelt die Genauigkeit der Vorhersagen des Modells wider. Während des Trainings verwendet ein Lernalgorithmus wie der Backpropagation-Algorithmus den Gradienten der Verlustfunktion in Bezug auf die Parameter des Modells, um diese Parameter anzupassen und den Verlust zu minimieren, wodurch die Leistung des Modells auf dem Datensatz effektiv verbessert wird.

Oft werden die Begriffe Verlustfunktion und Kostenfunktion synonym verwendet; trotzdem haben beide Begriffe unterschiedliche Definitionen:

Wie bereits erwähnt, gibt die Verlustfunktion, auch Fehlerfunktion genannt, an, wie gut eine einzelne Vorhersage des maschinellen Lernalgorithmus im Vergleich zum tatsächlichen Zielwert ist. Die wichtigste Erkenntnis ist, dass eine Verlustfunktion auf ein einzelnes Trainingsbeispiel angewendet wird und Teil des gesamten Lernprozesses des Modells ist, der das Signal liefert, mit dem der Lernalgorithmus des Modells die Gewichte und Parameter aktualisiert.

Die Kostenfunktion, die manchmal auch als Zielfunktion bezeichnet wird, ist ein Durchschnitt der Verlustfunktion einer ganzen Trainingsmenge, die mehrere Trainingsbeispiele enthält. Die Kostenfunktion quantifiziert die Leistung des Modells auf dem gesamten Trainingsdatensatz.

Schauen wir uns genauer an, wie Verlustfunktionen funktionieren.

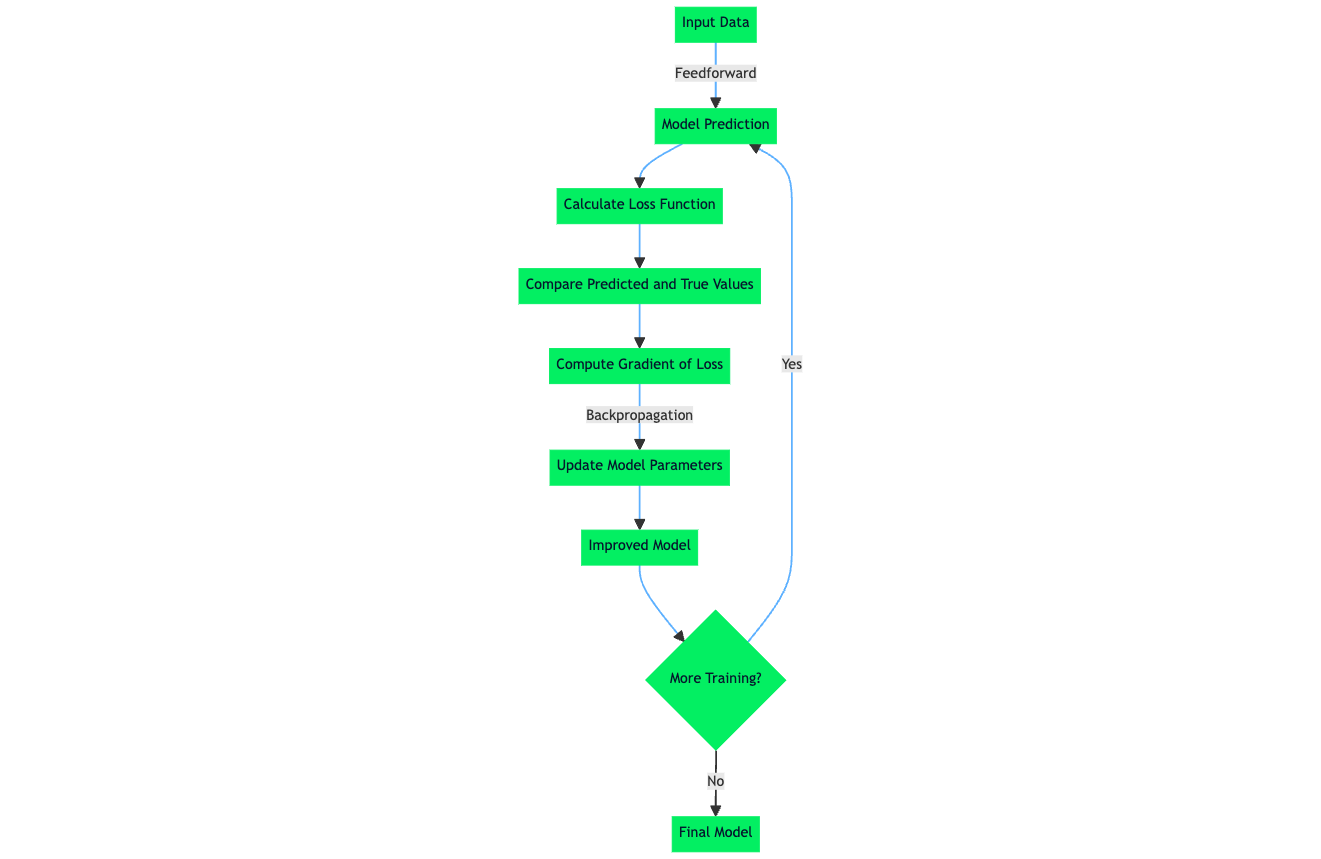
Wie Verlustfunktionen funktionieren

Es gibt zwar verschiedene Arten von Verlustfunktionen, aber im Grunde funktionieren sie alle, indem sie die Differenz zwischen den Vorhersagen eines Modus und dem tatsächlichen Zielwert im Datensatz quantifizieren. Der offizielle Begriff für diese numerische Quantifizierung ist der Vorhersagefehler. Der Lernalgorithmus und die Mechanismen in einem maschinellen Lernmodell werden so optimiert, dass der Vorhersagefehler minimiert wird. Das bedeutet, dass der Lernalgorithmus nach der Berechnung des Werts für die Verlustfunktion, der durch den Vorhersagefehler bestimmt wird, diese Informationen nutzt, um Gewichtungen und Parameter zu aktualisieren, was im nächsten Trainingsdurchgang zu einem geringeren Vorhersagefehler führt.

Wenn man sich mit Verlustfunktionen, Algorithmen für maschinelles Lernen und dem Lernprozess in neuronalen Netzen beschäftigt, kommt man auf das Thema empirische Risikominimierung (ERM). ERM ist ein Ansatz zur Auswahl der optimalen Parameter eines maschinellen Lernalgorithmus, der das empirische Risiko minimiert. Das empirische Risiko ist in diesem Fall der Trainingsdatensatz.

Die Risikominimierungskomponente des ERM ist der Prozess, durch den der interne Lernalgorithmus den Fehler der Vorhersage des maschinellen Lernalgorithmus für einen bekannten Datensatz minimiert, so dass das Modell eine erwartete Leistung und Genauigkeit in einem Szenario hat, in dem ein ungesehener Datensatz oder eine Datenstichprobe eine ähnliche statische Datenverteilung aufweisen könnte wie der Datensatz, für den das Modell ursprünglich trainiert wurde.

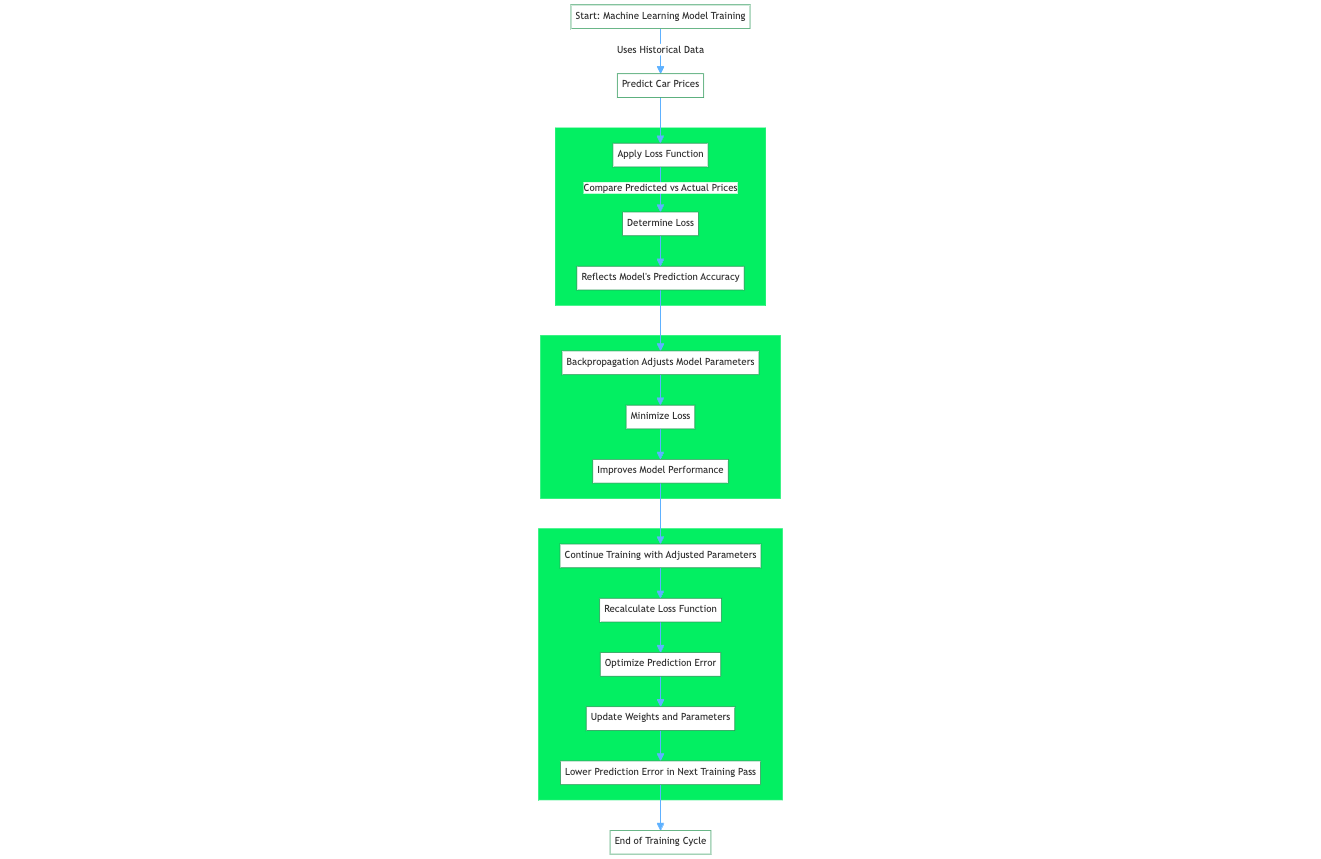
Arten von Verlustfunktionen

Verlustfunktionen beim maschinellen Lernen können nach den Aufgaben des maschinellen Lernens kategorisiert werden, auf die sie anwendbar sind. Die meisten Verlustfunktionen gelten für Regressions- und Klassifikationsprobleme beim maschinellen Lernen. Das Modell soll kontinuierliche Ausgabewerte für Regressionsaufgaben des maschinellen Lernens vorhersagen. Im Gegensatz dazu wird von dem Modell erwartet, dass es für Klassifizierungsaufgaben diskrete Labels liefert, die einer Datensatzklasse entsprechen.

Im Folgenden findest du Standardverlustfunktionen und ihre Einordnung in die Probleme des maschinellen Lernens, für die sie sich gut eignen. Die meisten dieser Verlustfunktionen werden später in diesem Artikel im Detail behandelt.

Verlustfunktionen für Regression

Mittlerer quadratischer Fehler (MSE) / L2-Verlust

Der mittlere quadratische Fehler (MSE) oder L2-Verlust ist eine Verlustfunktion, die das Ausmaß des Fehlers zwischen der Vorhersage eines maschinellen Lernalgorithmus und der tatsächlichen Ausgabe quantifiziert, indem sie den Durchschnitt der quadratischen Differenz zwischen den Vorhersagen und den Zielwerten bildet. Die Quadratur der Differenz zwischen den Vorhersagen und den tatsächlichen Zielwerten führt zu einer höheren Strafe für größere Abweichungen vom Zielwert. Ein Mittelwert der Fehler normalisiert die Gesamtfehler in Bezug auf die Anzahl der Stichproben in einem Datensatz oder einer Beobachtung.

Die mathematische Gleichung für den mittleren quadratischen Fehler (MSE) oder L2-Verlust lautet:

MSE = (1/n) * Σ(yᵢ - ȳ)²

Wo:

• n ist die Anzahl der Proben im Datensatz
• yᵢ ist der vorhergesagte Wert für die i-te Probe
• ȳ ist der Zielwert für die i-te Probe

Wann du MSE verwenden solltest

Bei der Entwicklung von Modellen für maschinelles Lernen ist es wichtig zu wissen, wann MSE eingesetzt werden sollte. MSE ist eine Standardverlustfunktion, die bei den meisten Regressionsaufgaben verwendet wird, da sie das Modell anweist, die quadratischen Unterschiede zwischen den vorhergesagten und den Zielwerten zu minimieren.

MSE wird für ML-Szenarien empfohlen, in denen es für den Lernprozess förderlich ist, das Vorhandensein von Ausreißern deutlich zu bestrafen. Diese Eigenschaften von MSE sind jedoch nicht immer für Szenarien und Anwendungsfälle geeignet, bei denen Ausreißer auf Rauschen in den Daten und nicht auf positive Signale zurückzuführen sind.

Ein Beispiel für den Einsatz der MSE-Verlustfunktion ist die Vorhersage von Immobilienpreisen oder, allgemeiner ausgedrückt, die Modellierung von Prognosen. Bei der Vorhersage von Hauspreisen werden Merkmale wie die Anzahl der Zimmer, die Lage, die Fläche, die Entfernung zu Annehmlichkeiten und andere numerische Merkmale berücksichtigt. Da die Hauspreise in einem bestimmten Gebiet normal verteilt sind, ist das Ziel, Ausreißer zu bestrafen, entscheidend für die Fähigkeit des Modells, genaue Hauspreise vorherzusagen.

Ein kleiner prozentualer Fehler in der Immobilienbranche kann eine beträchtliche Menge Geld ausmachen. Ein Fehler von 5 % bei einem Haus mit 200.000 USD ist zum Beispiel 10.000 USD und damit erheblich. Daher hilft die Quadrierung der Fehler (wie beim MSE) dabei, größeren Fehlern ein höheres Gewicht zu geben und so das Modell mit höherwertigen Eigenschaften präziser zu machen.

Mittlerer absoluter Fehler (MAE) / L1-Verlust

Der mittlere absolute Fehler (MAE), auch bekannt als L1-Verlust, ist eine Verlustfunktion, die bei Regressionsaufgaben verwendet wird und die durchschnittlichen absoluten Differenzen zwischen den vorhergesagten Werten eines maschinellen Lernmodells und den tatsächlichen Zielwerten berechnet. Im Gegensatz zum mittleren quadratischen Fehler (Mean Squared Error, MSE) werden bei der MAE die Differenzen nicht quadriert, sondern alle Fehler unabhängig von ihrer Größe gleich gewichtet.

Die mathematische Gleichung für den mittleren absoluten Fehler (MAE) oder L1-Verlust lautet:

MAE = (1/n) * Σ|yᵢ - ȳ|

Wo:

• n ist die Anzahl der Proben im Datensatz
• yᵢ ist der vorhergesagte Wert für die i-te Probe
• ȳ ist der Zielwert für die i-te Probe

Wann sollte MAE verwendet werden?

MAE misst die durchschnittliche absolute Differenz zwischen den vorhergesagten und den tatsächlichen Werten. Im Gegensatz zum MSE werden beim MAE die Differenzen nicht quadriert, was ihn weniger anfällig für Ausreißer macht. Im Vergleich zum mittleren quadratischen Fehler (Mean Squared Error, MSE) ist der mittlere absolute Fehler (Mean Absolute Error, MAE) von Natur aus weniger anfällig für Ausreißer, da er allen Fehlern unabhängig von ihrer Größe das gleiche Gewicht zuweist.

Das bedeutet, dass ein Ausreißer zwar den MSE erheblich verzerren kann, indem er einen unverhältnismäßig großen Fehler zum Quadrat beisteuert, seine Auswirkungen auf den MAE aber sehr viel geringer sind. Der Einfluss eines Ausreißers auf die Gesamtfehlermetrik ist minimal, wenn MAE als Verlustfunktion verwendet wird. Im Gegensatz dazu verstärkt der MSE den Effekt von Ausreißern durch die Quadrierung der Fehlerterme und wirkt sich somit stärker auf die Fehlerschätzung des Modells aus.

Ein Szenario, in dem MAE eine geeignete Verlustfunktion ist, ist ein Szenario, in dem wir Ausreißer nicht stark oder gar nicht bestrafen wollen, z. B. bei der Vorhersage von Lieferzeiten für einen Lebensmittellieferanten.

Ein Lieferdienstunternehmen wie UberEats, Deliveroo oder DoorDash könnte ein Schätzmodell für die Lieferung entwickeln, um die Kundenzufriedenheit zu erhöhen. Die Zeit, die ein Lieferdienst braucht, um die Lebensmittel auszuliefern, wird durch verschiedene Faktoren wie Wetter, Verkehrsstörungen, Baustellen usw. beeinflusst.

Der Umgang mit diesen Faktoren ist entscheidend für die Schätzung der Lieferzeiten. Eine Möglichkeit, damit umzugehen, ist, diese Ereignisse als Ausreißer zu klassifizieren, aber die Entscheidung so zu treffen, dass sie das trainierte Modell nicht beeinflussen. MAE ist in diesem Szenario eine geeignete Verlustfunktion, da sie Datenpunkte, die Ausreißer aufgrund von Baustellen oder seltenen Ereignissen sind, mit geringerer Strenge behandelt und so die Auswirkungen der Ausreißer auf die Fehlermetrik und den Lernprozess des Modells reduziert.

MAE fügt insbesondere eine einheitliche Fehlergewichtung zu allen Datenpunkten hinzu; in dem beschriebenen Szenario könnte die Bestrafung von Ausreißerdatenpunkten zu einer Über- oder Unterschätzung der Lieferzeiten führen.

Huber Loss / Glatter mittlerer absoluter Fehler

Huber Loss oder Smooth Mean Absolute Error ist eine Verlustfunktion, die die vorteilhaften Eigenschaften der Verlustfunktionen Mean Absolute Error und Mean Squared Error in einer einzigen Verlustfunktion zusammenfasst. Die hybride Natur von Huber Loss macht ihn weniger empfindlich gegenüber Ausreißern, genau wie MAE, bestraft aber auch kleinere Fehler innerhalb der Datenstichprobe, ähnlich wie MSE. Die Huber-Loss-Funktion wird auch beim maschinellen Regressionslernen verwendet.

Die mathematische Gleichung für den Huber-Verlust lautet wie folgt:

L(δ, y, f(x)) = (1/2) * (f(x) - y)^2   if |f(x) - y| <= δ
               = δ * |f(x) - y| - (1/2) * δ^2   if |f(x) - y| > δ

Wo:

• L steht für die Huber-Loss-Funktion
• δ ist der Delta-Parameter, der den Schwellenwert für den Wechsel zwischen der quadratischen und der linearen Komponente der Verlustfunktion bestimmt
• y ist der wahre Wert oder Zielwert
• f(x) ist der vorhergesagte Wert

Wann man Huber Loss / Smooth Mean Absolute Error verwenden sollte

Die Huber-Loss-Funktion kombiniert effektiv zwei Komponenten für die unterschiedliche Behandlung von Fehlern, wobei der Übergangspunkt zwischen diesen Komponenten durch den Schwellenwert δ bestimmt wird:

• Quadratische Komponente bei kleinen Fehlern: Für Fehler, die kleiner als δ sind, wird die quadratische Komponente verwendet (1/2) * (f(x) - y)^2
• Lineare Komponente bei großen Fehlern: Für Fehler, die größer als δ sind, wird die lineare Komponente angewendet δ * |f(x) - y| - (1/2) * δ^2

Der Huber-Verlust arbeitet in zwei Modi, die je nach Größe der berechneten Differenz zwischen dem tatsächlichen Zielwert und der Vorhersage des maschinellen Lernalgorithmus umgeschaltet werden. Der Schlüsselbegriff bei Huber Loss ist Delta (δ). Delta ist ein Schwellenwert, der die numerische Grenze festlegt, bei der der Huber Loss die quadratische Anwendung des Verlusts oder die lineare Berechnung verwendet.

Die quadratische Komponente von Huber Loss charakterisiert die Vorteile von MSE, die Ausreißer bestrafen; innerhalb von Huber Loss wird dies auf Fehler angewandt, die kleiner als Delta sind, was eine genauere Vorhersage des Modells gewährleistet.

Angenommen, der berechnete Fehler, also die Differenz zwischen dem tatsächlichen und dem vorhergesagten Wert, ist größer als das Delta. In diesem Fall nutzt Huber Loss die lineare Berechnung des Verlusts ähnlich wie MAE, wobei die Empfindlichkeit gegenüber der Fehlergröße geringer ist, um sicherzustellen, dass das trainierte Modell große Fehler nicht überbewertet, insbesondere wenn der Datensatz Ausreißer oder unwahrscheinliche Datenproben enthält.

Verlustfunktionen für die Klassifizierung

Binärer Cross-Entropie-Verlust / Log-Verlust

Binary Cross-Entropy Loss (BCE) ist ein Leistungsmaß für Klassifizierungsmodelle, das eine Vorhersage mit einem Wahrscheinlichkeitswert ausgibt, der typischerweise zwischen 0 und 1 liegt, und dieser Vorhersagewert entspricht der Wahrscheinlichkeit, dass eine Datenprobe zu einer Klasse oder Kategorie gehört. Beim binären Cross-Entropie-Verlust gibt es zwei verschiedene Klassen. Eine Variante des Cross-Entropie-Verlusts, die kategoriale Cross-Entropie, ist auf Mehrklassen-Klassifizierungsszenarien anwendbar.

Um den binären Cross-Entropie-Verlust zu verstehen, der manchmal auch Log-Verlust genannt wird, ist es hilfreich, die Komponenten der Begriffe zu diskutieren.

• Verlust: Dies ist eine mathematische Quantifizierung der Spanne/Differenz zwischen der Vorhersage eines maschinellen Lernalgorithmus und dem tatsächlichen Zielwert.
• Entropie: Eine einfache Definition von Entropie ist, dass sie den Grad der Zufälligkeit oder Unordnung in einem System berechnet
• Cross Entropy: Dieser Begriff wird in der Informationstheorie häufig verwendet und misst die Unterschiede zwischen zwei Wahrscheinlichkeitsverteilungen, die zur Identifizierung einer Beobachtung verwendet werden können.
• Binär: Dies ist ein Ausdruck von numerischen Ziffern, der einen der beiden Zustände, 0 oder 1, verwendet. Dies wird auf die Definition der binären Klassifizierung ausgedehnt, bei der wir zwei Klassen (A und B) mit Hilfe der binären Darstellung unterscheiden, wobei der Klasse A die numerische Darstellung 0 und der Klasse B die 1 zugewiesen wird.

Der binäre Cross-Entropie-Verlust (oder Log-Verlust) ist eine Quantifizierung der Differenz zwischen der Vorhersage eines maschinellen Lernalgorithmus und der tatsächlichen Zielvorhersage, die sich aus dem negativen Wert der Summierung des Logarithmuswerts der Wahrscheinlichkeiten der vom maschinellen Lernalgorithmus gemachten Vorhersagen gegen die Gesamtzahl der Datenproben errechnet. BCE wird in Anwendungsfällen des maschinellen Lernens eingesetzt, bei denen es sich um logistische Regressionsprobleme und um das Training künstlicher neuronaler Netze handelt, die die Wahrscheinlichkeit der Zugehörigkeit einer Datenprobe zu einer Klasse vorhersagen und die sigmoide Aktivierungsfunktion intern nutzen sollen.

Die mathematische Gleichung für den Binary Cross-Entropy Loss, auch bekannt als Log Loss, lautet:

L(y, f(x)) = -[y * log(f(x)) + (1 - y) * log(1 - f(x))]

Wo:

• L steht für die binäre Cross-Entropy-Verlustfunktion
• y ist das wahre binäre Label (0 oder 1)
• f(x) ist die vorhergesagte Wahrscheinlichkeit für die positive Klasse (zwischen 0 und 1)

Wann wird der binäre Cross-Entropie-Verlust / Log-Verlust verwendet?

Die obige Gleichung gilt speziell für ein Szenario, in dem der Algorithmus für maschinelles Lernen eine Klassifizierung zwischen zwei Klassen vornimmt. Dies ist ein binäres Klassifizierungsszenario.

Wie in der Gleichung durch das negative Symbol angegeben: '-' BCE berechnet den Verlust, indem es das Negativ von zwei Termen und bei mehreren Vorhersagen oder Datenproben den Durchschnitt des Negativs der beiden folgenden Terme ermittelt:

1. Der Logarithmus der vom Modell vorhergesagten Wahrscheinlichkeit, dass die positive Klasse vorhanden ist y * log(f(x))
2. Der Logarithmus von 1 minus der vorhergesagten Wahrscheinlichkeit für die negative Klasse: (1 - y) * log(1 - f(x))

Die BCE-Verlustfunktion bestraft ungenaue Vorhersagen, d. h. Vorhersagen, die sich deutlich von der positiven Klasse unterscheiden oder, mit anderen Worten, eine hohe Entropie aufweisen. Wenn BCE als Komponente in Lernalgorithmen verwendet wird, ermutigt dies das Modell, seine Vorhersagen zu verfeinern, die Wahrscheinlichkeiten für die entsprechende Klasse während des Trainings sind.

Scharnierverlust

Hinge Loss ist eine Verlustfunktion, die beim maschinellen Lernen verwendet wird, um Klassifikatoren zu trainieren, die den Abstand zwischen Datenpunkten und der Entscheidungsgrenze vergrößern. Sie wird daher hauptsächlich für Klassifizierungen mit maximaler Marge verwendet. Um einen maximalen Spielraum zwischen den Datenpunkten und den Grenzen zu gewährleisten, bestraft der Scharnierverlust Vorhersagen des maschinellen Lernmodells, die falsch klassifiziert sind, d. h. Vorhersagen, die auf der falschen Seite der Spielraumgrenze liegen, und auch Vorhersagen, die richtig klassifiziert sind, sich aber in unmittelbarer Nähe der Entscheidungsgrenze befinden.

Diese Eigenschaft der Hinge-Loss-Funktion stellt sicher, dass maschinelle Lernmodelle in der Lage sind, die genaue Zuordnung von Datenpunkten zu ihrem Zielwert mit einem Vertrauen vorherzusagen, das den Schwellenwert der Entscheidungsgrenze übersteigt. Diese Herangehensweise an das maschinelle Lernen von Algorithmen verbessert die Verallgemeinerungsfähigkeiten des Modells, sodass es Datenpunkte mit einem hohen Grad an Sicherheit genau klassifizieren kann.

Die mathematische Gleichung für den Scharnierverlust lautet:

L(y, f(x)) = max(0, 1 - y * f(x))

Wo:

• L steht für den Scharnierverlust
• y ist das wahre Label oder der Zielwert (-1 oder 1)
• f(x) ist der vorhergesagte Wert oder die Ausgabe der Entscheidungsfunktion

Die Wahl der richtigen Verlustfunktion

Die Auswahl der geeigneten Verlustfunktion für einen Algorithmus des maschinellen Lernens ist von entscheidender Bedeutung, da die Leistung des Modells stark von der Fähigkeit des Algorithmus abhängt, seine internen Gewichte zu erlernen oder anzupassen, um sie an einen Datensatz anzupassen.

Die Leistung eines maschinellen Lernmodells oder -algorithmus wird durch die verwendete Verlustfunktion bestimmt, vor allem weil die Komponente der Verlustfunktion den Lernalgorithmus beeinflusst, der verwendet wird, um den Fehlerverlust oder den Kostenfunktionswert des Modells zu minimieren. Die Verlustfunktion wirkt sich im Wesentlichen auf die Fähigkeit des Modells aus, zu lernen und den Wert seiner internen Gewichte an die Muster in einem Datensatz anzupassen.

Wenn die Verlustfunktion richtig gewählt ist, kann der Lernalgorithmus während der Trainingsphase effektiv zu einem optimalen Verlust konvergieren und gut auf ungesehene Datenproben verallgemeinern. Eine angemessen gewählte Verlustfunktion dient als Leitfaden, der den Lernalgorithmus in Richtung Genauigkeit und Zuverlässigkeit lenkt und sicherstellt, dass er die zugrundeliegenden Muster in den Daten erfasst und gleichzeitig ein Overfitting oder Underfitting vermeidet.

Faktoren, die bei der Auswahl einer Verlustfunktion zu berücksichtigen sind

Wenn du die Art des maschinellen Lernproblems verstehst, kannst du die Kategorie der zu verwendenden Verlustfunktion bestimmen. Für verschiedene Machine-Learning-Probleme gelten unterschiedliche Verlustfunktionen.

Klassifizierung vs. Regression

Bei Aufgaben des maschinellen Lernens zur Klassifizierung geht es normalerweise darum, Datenpunkte einer bestimmten Kategorie zuzuordnen. Bei dieser Art von maschinellen Lernaufgaben ist die Ausgabe des maschinellen Lernmodells in der Regel eine Reihe von Wahrscheinlichkeiten, die bestimmen, wie wahrscheinlich es ist, dass ein Datenpunkt einer bestimmten Bezeichnung entspricht.

Die Kreuzentropie-Verlustfunktion wird häufig für Klassifizierungsaufgaben verwendet. Bei einer Regressionsaufgabe des maschinellen Lernens, bei der das Ziel darin besteht, dass ein maschinelles Lernmodell eine Vorhersage auf der Grundlage einer Reihe von Eingaben erstellt, sind Verlustfunktionen wie der mittlere quadratische Fehler oder der mittlere absolute Fehler besser geeignet.

Binäre vs. Multiklassen-Klassifizierung

Bei der binären Klassifizierung werden die Datenproben in zwei verschiedene Kategorien eingeteilt, während bei der Multiklassenklassifizierung, wie der Name schon sagt, die Datenproben in mehr als zwei Kategorien eingeteilt werden. Bei Klassifizierungsproblemen des maschinellen Lernens, die nur zwei Klassen umfassen (binäre Klassifizierung), ist es am besten, eine binäre Kreuzentropie-Verlustfunktion zu verwenden. In Situationen, in denen mehr als zwei Klassen das Ziel der Vorhersage sind, sollte die kategoriale Kreuzentropie verwendet werden.

Empfindlichkeit

Ein weiterer zu berücksichtigender Faktor ist die Empfindlichkeit der Verlustfunktion gegenüber Ausreißern. In manchen Szenarien ist es wünschenswert, dass Ausreißer und Datenproben, die die gesamte statistische Verteilung des Datensatzes verzerren, während des Trainings bestraft werden; in solchen Szenarien sind Verlustfunktionen wie der mittlere quadratische Fehler geeignet.

Es gibt zwar Szenarien, in denen eine geringere Sensibilität für Ausreißer erforderlich ist, aber das sind Szenarien, in denen Ausreißer "nie vorkommen" oder unwahrscheinlich sind. Bei diesem Ziel könnte die Bestrafung von Ausreißern zu einem nicht leistungsfähigen Modell führen. Eine Verlustfunktion wie der mittlere absolute Fehler ist in solchen Szenarien anwendbar. Um das Beste aus beiden Welten zu erhalten, sollten Praktiker die Huber-Verlustfunktion in Betracht ziehen, die Komponenten enthält, die Ausreißer mit niedrigen Fehlerwerten bestrafen und die Empfindlichkeit des Modells gegenüber Ausreißern mit großen Fehlerwerten verringern.

Berechnungseffizienz

Computerressourcen sind im Bereich des maschinellen Lernens, in der Wirtschaft und in der Forschung ein wichtiges Gut. Der Zugang zu großen Rechnerkapazitäten ermöglicht es den Praktikern, mit großen Datensätzen zu experimentieren und komplexere Machine-Learning-Probleme zu lösen. Einige Verlustfunktionen sind rechenintensiver als andere, vor allem wenn die Anzahl der Datensätze groß ist. Daher ist die Berechnungseffizienz einer Verlustfunktion ein Faktor, der bei der Auswahl einer Verlustfunktion berücksichtigt werden muss.

Auswirkungen von Ausreißern und Datenverteilung

Ausreißer sind Datenproben, die aus der allgemeinen statistischen Verteilung eines Datensatzes herausfallen; sie werden manchmal auch als Anomalien oder Unregelmäßigkeiten bezeichnet. Wie mit Ausreißern umgegangen wird, bestimmt die Leistung und Genauigkeit des trainierten maschinellen Lernmodells.

Wie bereits erwähnt, wirken sich Ausreißer in Datensätzen auf die in Verlustfunktionen verwendeten Fehlerwerte aus, je nachdem, welche Verlustfunktion verwendet wird. Die Wirkung von Ausreißern auf die Verlustfunktionen überträgt sich auf das Ergebnis des Lernprozesses des maschinellen Lernalgorithmus, was zu beabsichtigtem oder unbeabsichtigtem Verhalten des maschinellen Lernalgorithmus oder Modells führen kann.

Der mittlere quadratische Fehler bestraft zum Beispiel Ausreißer, die zu großen Fehlerwerten/Termen beitragen; das bedeutet, dass während des Trainingsprozesses die Modellgewichte angepasst werden, um zu lernen, wie diese Ausreißer berücksichtigt werden können. Auch hier gilt: Wenn dies nicht das beabsichtigte Verhalten des maschinellen Lernmodells ist, wird das nach dem Training erstellte Modell eine schlechte Generalisierung auf ungesehene Daten aufweisen. Für Szenarien, in denen die Auswirkungen von Ausreißern gemildert werden müssen, sind Funktionen wie MAE und Huber Loss besser geeignet.

Verlustfunktionen implementieren

Beispiele für die Umsetzung gängiger Verlustfunktionen

Implementierung von MAE in Python

# Python implementation of Mean Absolute Error (MAE)

def mean_absolute_error(actual:list, predicted:list) -> float:
    """
    Calculate the Mean Absolute Error between actual and predicted values

    :param actual: list, actual values
    :param predicted: list, predicted values
    :return: float, the calculated MAE
    """
    # Ensure the length of the two lists are the same
    if len(actual) != len(predicted):
        raise ValueError("The length of actual values and predicted values must be the same")

    # Calculate the absolute differences
    absolute_diffs = [abs(act - pred) for act, pred in zip(actual, predicted)]
    
    # Calculate the mean of the absolute differences
    mae = sum(absolute_diffs) / len(actual)
    
    return mae

# Example usage:
# actual values
y_true = [3, -0.5, 2, 7]

# predicted values
y_pred = [2.5, 0.0, 2, 8]

# Calculate MAE
mae_value = mean_absolute_error(y_true, y_pred)
print(mae_value)
# 0.5

Implementierung von MSE in Python

# Python implementation of Mean Squared Error (MSE) / L2 Loss

def mean_squared_error(actual:list, predicted:list) -> float:
    """
    Calculate the Mean Squared Error between actual and predicted values

    :param actual: list, actual values
    :param predicted: list ,predicted values
    :return: float, the calculated MSE
    """
    # Ensure the length of the two lists are the same
    if len(actual) != len(predicted):
        raise ValueError("The length of actual values and predicted values must be the same")

    # Calculate the squared differences
		# (yᵢ - ȳ)²
    squared_diffs = [(act - pred) ** 2 for act, pred in zip(actual, predicted)]
    
    # Calculate the mean of the squared differences
    mse = sum(squared_diffs) / len(actual)
    
    return mse

# Example usage:
# actual values
y_true = [1, 2, 3, 4, 5]

# predicted values
y_pred = [1.1, 2.2, 2.9, 4.1, 4.9]

# Calculate MSE
mse_value = mean_squared_error(y_true, y_pred)
print(mse_value)
# 0.015999999999999993

Die Verwendung von Bibliotheken für die Implementierung von Verlustfunktionen

Zwar ist eine benutzerdefinierte Implementierung von Verlustfunktionen möglich, und Deep-Learning-Bibliotheken wie TensorFlow und PyTorch unterstützen die Verwendung benutzerdefinierter Verlustfunktionen in neuronalen Netzwerkimplementierungen, aber Bibliotheken wie Scikit-learn, TensorFlow und PyTorch bieten integrierte Implementierungen von häufig verwendeten Verlustfunktionen.

Diese vorintegrierten Funktionen ermöglichen eine einfache Nutzung und abstrahieren die Komplexität, die mit der Implementierung dieser Verlustfunktionen verbunden ist, wodurch der Entwicklungsprozess für maschinelle Lernmodelle vereinfacht wird.

Die Verwendung dieser Deep-Learning-Bibliotheken bietet Vorteile gegenüber reinen Python-Implementierungen, von denen einige sind:

• Einfachheit der Nutzung
• Effizienz und Optimierung
• Unterstützung für GPUs und parallele Berechnungen
• Unterstützung der Entwicklergemeinschaft

Mittlerer absoluter Fehler (MAE) mit der scikit-learn-Bibliothek

from sklearn.metrics import mean_absolute_error

# actual values
y_true = [3, -0.5, 2, 7]

# predicted values
y_pred = [2.5, 0.0, 2, 8]

# Calculate MAE using scikit-learn
mae_value = mean_absolute_error(y_true, y_pred)
print(mae_value)
#0.5

Mittlerer quadratischer Fehler (MSE) mit der Scikit-Learn-Bibliothek

from sklearn.metrics import mean_squared_error

# actual values
y_true = [1, 2, 3, 4, 5]

# predicted values
y_pred = [1.1, 2.2, 2.9, 4.1, 4.9]

# Calculate MSE using scikit-learn
mse_value = mean_squared_error(y_true, y_pred)
print(mse_value)
# 0.016

Fazit

Zusammenfassend lässt sich sagen, dass die Wahl der richtigen Verlustfunktion für ein effektives maschinelles Lernmodelltraining entscheidend ist. Dieser Artikel beleuchtet die wichtigsten Verlustfunktionen, ihre Rolle in Algorithmen für maschinelles Lernen und ihre Eignung für verschiedene Aufgaben. Vom mittleren quadratischen Fehler (Mean Squared Error, MSE) bis zum Huber-Loss hat jede Funktion ihre eigenen Vorteile, sei es beim Umgang mit Ausreißern oder beim Ausgleich von Verzerrungen und Varianz.

Die Entscheidung, ob man benutzerdefinierte oder vorgefertigte Verlustfunktionen aus Bibliotheken wie Scikit-learn, TensorFlow und PyTorch verwendet, hängt von den spezifischen Projektanforderungen, der Recheneffizienz und der Erfahrung des Nutzers ab. Diese Bibliotheken sind einfach zu implementieren, werden von der Community unterstützt und regelmäßig aktualisiert.

Trotz der Weiterentwicklung des maschinellen Lernens bleibt die Bedeutung von Verlustfunktionen konstant. Künftige Trends werden vielleicht noch speziellere Verlustfunktionen hervorbringen, aber die grundlegenden Prinzipien werden wahrscheinlich bestehen bleiben. Wenn du tiefer in das maschinelle Lernen und seine Anwendungen eintauchen möchtest, solltest du den DataCamp-Track "Machine Learning Scientist with Python" besuchen.