Cursus
L'apprentissage automatique fournit des modèles informatiques capables de faire des prédictions, des classifications et des décisions basées sur des données. En tant que domaine d'étude, l'apprentissage automatique est un sous-ensemble du domaine de l'intelligence artificielle, qui englobe les processus impliqués dans la construction d'un modèle informatique doté de capacités qui imitent l'intelligence humaine et, dans certains cas, la surpassent.
L'apprentissage automatique et les algorithmes et techniques associés impliquent fondamentalement la conception, la mise en œuvre et la formation d'algorithmes pour reconnaître des modèles dans des données exposées et effectuer des prédictions ou des classifications.
Les algorithmes d'apprentissage automatique apprennent par différentes méthodes, mais un élément fondamental du processus d'apprentissage des algorithmes et modèles d'apprentissage automatique est la fonction de perte. La fonction de perte est un processus mathématique qui quantifie la marge d'erreur entre la prédiction d'un modèle et la valeur cible réelle. Dans la suite de cet article, nous étudierons en détail la fonction de perte.
Devenez un scientifique ML
Les fonctions de perte en bref
L'essentiel est que la fonction de perte est un moyen mesurable d'évaluer les performances et la précision d'un modèle d'apprentissage automatique. Dans ce cas, la fonction de perte sert de guide pour le processus d'apprentissage au sein d'un modèle ou d'un algorithme d'apprentissage automatique.
Le rôle de la fonction de perte est crucial dans la formation des modèles d'apprentissage automatique et comprend les éléments suivants :
- Mesure de la performance: Les fonctions de perte permettent d'évaluer clairement les performances d'un modèle en quantifiant la différence entre les prévisions et les résultats réels.
- Améliorations à apporter: Les fonctions de perte guident l'amélioration du modèle en demandant à l'algorithme d'ajuster les paramètres (poids) de manière itérative afin de réduire les pertes et d'améliorer les prévisions.
- Équilibrer le biais et la variance: Des fonctions de perte efficaces permettent d'équilibrer le biais du modèle (simplification excessive) et la variance (surajustement), ce qui est essentiel pour la généralisation du modèle à de nouvelles données.
- Influencer le comportement du modèle: Certaines fonctions de perte peuvent affecter le comportement du modèle, par exemple en le rendant plus robuste face aux données aberrantes ou en donnant la priorité à certains types d'erreurs.
Nous étudierons les rôles de certaines fonctions de perte dans les sections suivantes et nous développerons une intuition et une compréhension détaillées de la fonction de perte.
Qu'est-ce qu'une fonction de perte ?
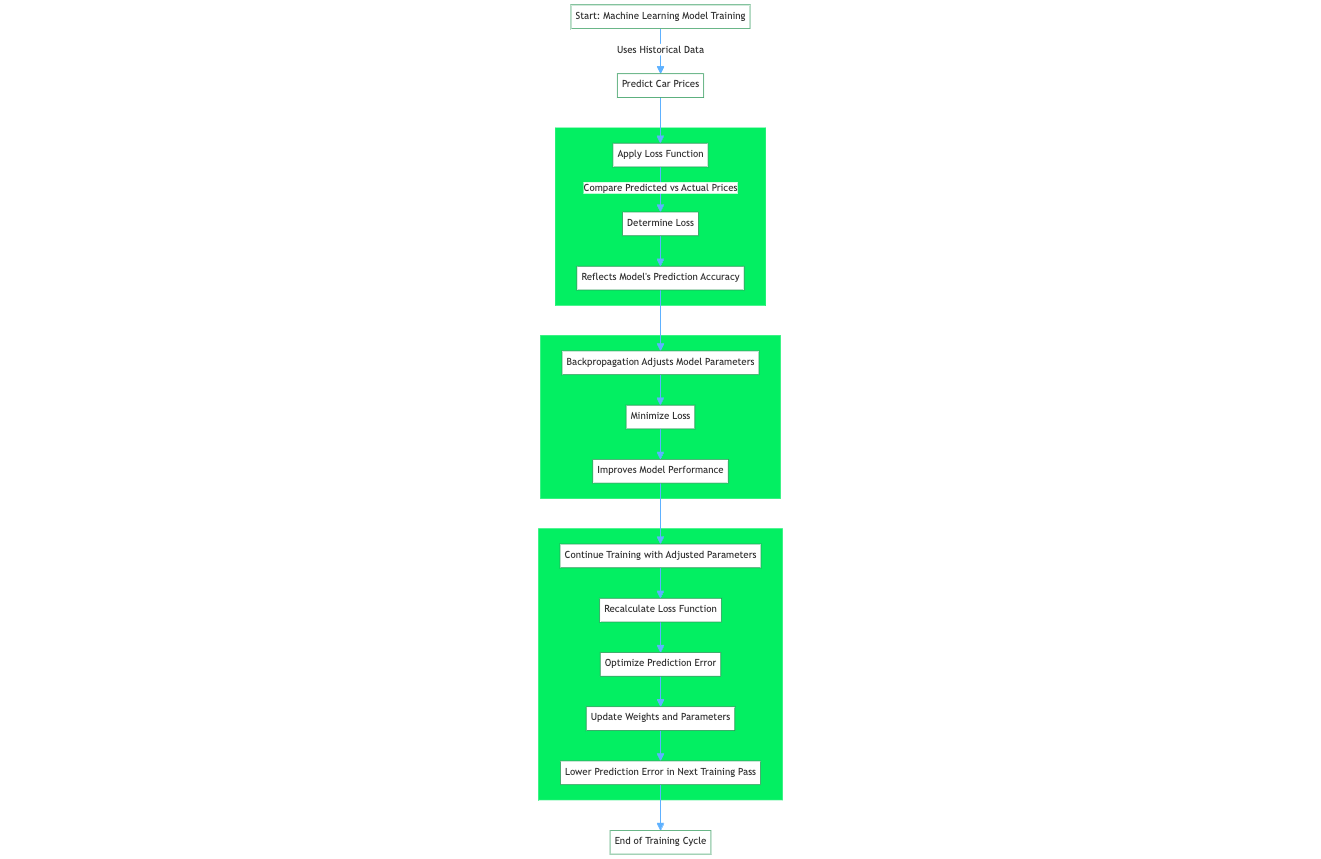
La fonction de perte, également appelée fonction d'erreur, est un élément essentiel de l'apprentissage automatique qui quantifie la différence entre les sorties prédites par un algorithme d'apprentissage automatique et les valeurs cibles réelles. Par exemple, dans le cadre d'un problème de régression visant à prédire les prix des voitures sur la base de données historiques, une fonction de perte évalue la prédiction d'un réseau neuronal sur la base d'un échantillon d'apprentissage provenant de l'ensemble de données d'apprentissage. La fonction de perte quantifie l'écart ou la marge d'erreur entre le prix de la voiture prédit par le réseau et le prix réel.
La valeur résultante, la perte, reflète la précision des prédictions du modèle. Pendant la formation, un algorithme d'apprentissage tel que l'algorithme de rétropropagation utilise le gradient de la fonction de perte par rapport aux paramètres du modèle pour ajuster ces paramètres et minimiser la perte, améliorant ainsi efficacement les performances du modèle sur l'ensemble de données.
Les termes "fonction de perte" et "fonction de coût" sont souvent utilisés de manière interchangeable, mais ils ont tous deux des définitions distinctes :
Comme indiqué précédemment, la fonction de perte, également connue sous le nom de fonction d'erreur, quantifie la qualité d'une prédiction unique de l'algorithme d'apprentissage automatique par rapport à la valeur cible réelle. L'essentiel est qu' une fonction de perte s'applique à un seul exemple d'apprentissage et fait partie du processus d'apprentissage global du modèle qui fournit le signal par lequel l'algorithme d'apprentissage du modèle met à jour les poids et les paramètres.
La fonction de coût, parfois appelée fonction objective, est une moyenne de la fonction de perte d'un ensemble de formation contenant plusieurs exemples de formation. La fonction de coût quantifie les performances du modèle sur l'ensemble des données d'apprentissage.
Voyons plus en détail comment fonctionnent les fonctions de perte.
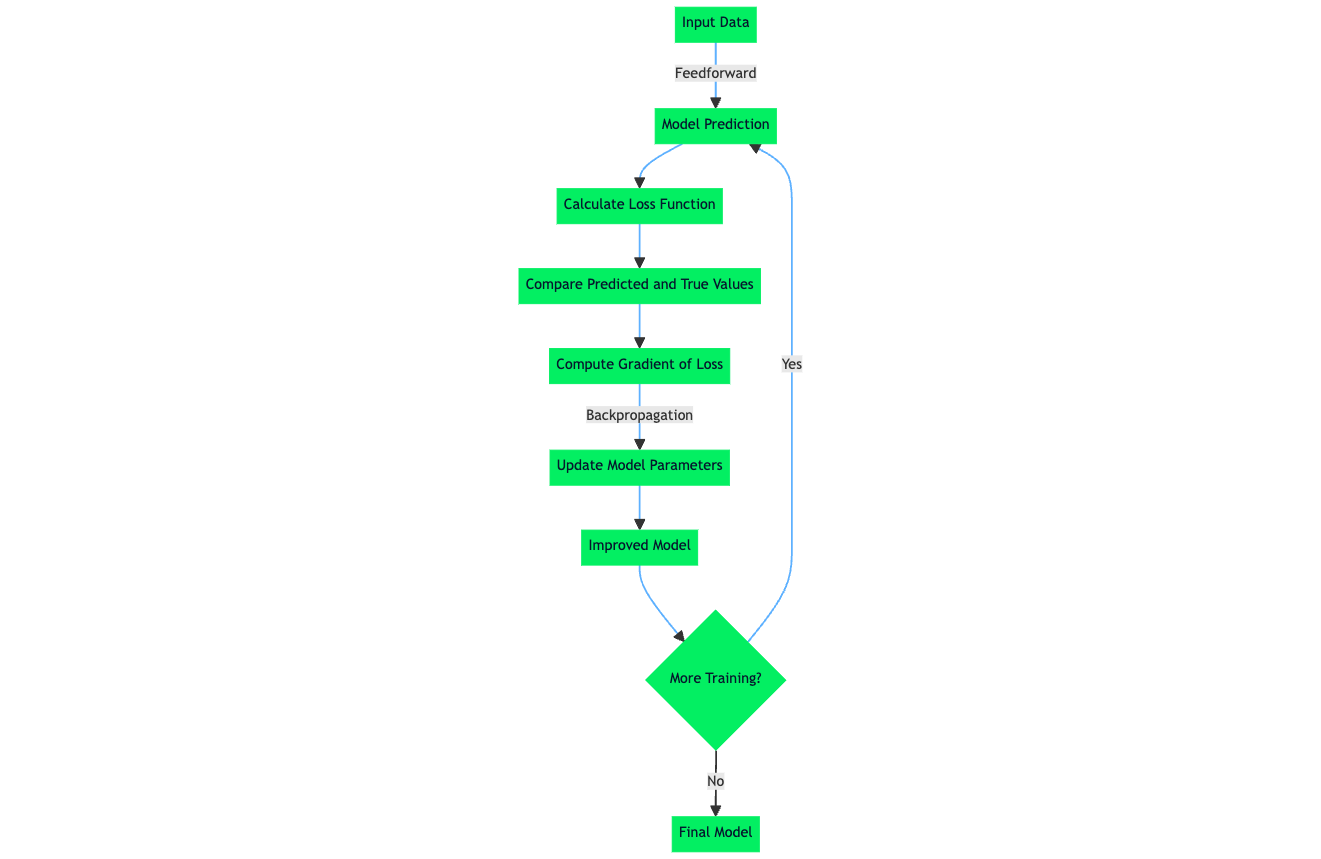
Fonctionnement des fonctions de perte
Bien qu'il existe différents types de fonctions de perte, elles fonctionnent toutes en quantifiant la différence entre les prédictions d'un mode et la valeur cible réelle dans l'ensemble de données. Le terme officiel pour cette quantification numérique est l'erreur de prédiction. L'algorithme d'apprentissage et les mécanismes d'un modèle d'apprentissage automatique sont optimisés pour minimiser l'erreur de prédiction, ce qui signifie qu'après le calcul de la valeur de la fonction de perte, qui est déterminée par l'erreur de prédiction, l'algorithme d'apprentissage tire parti de cette information pour procéder à des mises à jour de poids et de paramètres qui, en fait, au cours de la prochaine période d'apprentissage, conduisent à une erreur de prédiction plus faible.
Lorsque l'on explore le sujet des fonctions de perte, des algorithmes d'apprentissage automatique et du processus d'apprentissage au sein des réseaux neuronaux, la question de la minimisation empirique du risque (MRE) se pose. L'ERM est une approche permettant de sélectionner les paramètres optimaux d'un algorithme d'apprentissage automatique qui minimise le risque empirique. Le risque empirique, dans ce cas, est l'ensemble de données de formation.
La composante "minimisation du risque" de l'ERM est le processus par lequel l'algorithme d'apprentissage interne minimise l'erreur de prédiction de l'algorithme d'apprentissage automatique pour un ensemble de données connu, de sorte que le modèle a une performance et une précision attendues dans un scénario où un ensemble de données ou un échantillon de données non vu qui pourrait avoir une distribution de données statiques similaire à l'ensemble de données sur lequel le modèle a été initialement formé.
Types de fonctions de perte
Les fonctions de perte dans l'apprentissage automatique peuvent être classées en fonction des tâches d'apprentissage automatique auxquelles elles s'appliquent. La plupart des fonctions de perte s'appliquent aux problèmes de régression et de classification de l'apprentissage automatique. Le modèle est censé prédire des valeurs de sortie continues pour les tâches d'apprentissage automatique par régression. En revanche, le modèle est censé fournir des étiquettes discrètes correspondant à une classe de l'ensemble de données pour les tâches de classification.
Vous trouverez ci-dessous des fonctions de perte standard et leur classification en fonction des problèmes d'apprentissage automatique auxquels elles se prêtent. La plupart de ces fonctions de perte sont traitées en détail plus loin dans cet article.
|
Fonction de perte |
Applicabilité à la classification |
Applicabilité à la régression |
|
Erreur quadratique moyenne (EQM) / Perte L2 |
✖️ |
✔️ |
|
Erreur absolue moyenne (MAE) / Perte L1 |
✖️ |
✔️ |
|
Perte d'entropie croisée binaire / Perte logarithmique |
✔️ |
✖️ |
|
Perte catégorielle d'entropie croisée |
✔️ |
✖️ |
|
Perte de charnière |
✔️ |
✖️ |
|
Perte de Huber / Erreur absolue moyenne lisse |
✖️ |
✔️ |
|
Perte de logs |
✔️ |
✖️ |
Fonctions de perte pour la régression
Erreur quadratique moyenne (EQM) / Perte L2
L'erreur quadratique moyenne (EQM) ou perte L2 est une fonction de perte qui quantifie l'ampleur de l'erreur entre la prédiction d'un algorithme d'apprentissage automatique et une sortie réelle en prenant la moyenne de la différence quadratique entre les prédictions et les valeurs cibles. La mise au carré de la différence entre les prédictions et les valeurs cibles réelles entraîne une pénalité plus élevée pour les écarts plus importants par rapport à la valeur cible. La moyenne des erreurs normalise les erreurs totales par rapport au nombre d'échantillons d'un ensemble de données ou d'une observation.
L'équation mathématique de l'erreur quadratique moyenne (EQM) ou de la perte L2 est la suivante :
MSE = (1/n) * Σ(yᵢ - ȳ)²Où ?
- n est le nombre d'échantillons dans l'ensemble de données
- yᵢ est la valeur prédite pour le i-ième échantillon
- ȳ est la valeur cible pour le i-ième échantillon
Quand utiliser MSE ?
Il est essentiel de savoir quand utiliser l'ESM dans le cadre du développement de modèles d'apprentissage automatique. L'EQM est une fonction de perte standard utilisée dans la plupart des tâches de régression, car elle demande au modèle d'optimiser pour minimiser les différences au carré entre les valeurs prédites et les valeurs cibles.
MSE est recommandé pour les scénarios de ML dans lesquels il est favorable au processus d'apprentissage de pénaliser de manière significative la présence de valeurs aberrantes. Toutefois, ces caractéristiques de l'EQM ne sont pas toujours adaptées aux scénarios et aux cas d'utilisation dans lesquels les valeurs aberrantes sont dues au bruit des données plutôt qu'à des signaux positifs.
La prévision des prix de l'immobilier ou, plus généralement, la modélisation prédictive, est un exemple de scénario dans lequel la fonction de perte MSE est exploitée. Pour prédire les prix des logements, il faut utiliser des caractéristiques telles que le nombre de pièces, l'emplacement, la superficie, la distance par rapport aux commodités et d'autres caractéristiques numériques. Les prix des logements dans une zone localisée sont normalement distribués, de sorte que l'objectif consistant à pénaliser les valeurs aberrantes est essentiel à la capacité du modèle à prédire des prix précis.
Dans le domaine de l'immobilier, une petite erreur de pourcentage peut se traduire par une somme d'argent considérable. Par exemple, une erreur de 5 % sur une maison de 200 000 dollars représente 10 000 dollars, ce qui est considérable. Par conséquent, la mise au carré des erreurs (comme dans le cas de l'EQM) permet de donner plus de poids aux erreurs les plus importantes, poussant ainsi le modèle à être plus précis avec des propriétés de plus grande valeur.
Erreur absolue moyenne (MAE) / Perte L1
L'erreur absolue moyenne (MAE), également connue sous le nom de perte L1, est une fonction de perte utilisée dans les tâches de régression qui calcule les différences absolues moyennes entre les valeurs prédites par un modèle d'apprentissage automatique et les valeurs cibles réelles. Contrairement à l'erreur quadratique moyenne (MSE), la MAE n'élève pas les différences au carré, traitant toutes les erreurs avec le même poids, quelle que soit leur ampleur.
L'équation mathématique de l'erreur absolue moyenne (MAE) ou de la perte L1 est la suivante :
MAE = (1/n) * Σ|yᵢ - ȳ|Où ?
- n est le nombre d'échantillons dans l'ensemble de données
- yᵢ est la valeur prédite pour le i-ième échantillon
- ȳ est la valeur cible pour le i-ième échantillon
Quand utiliser MAE
Le MAE mesure la différence absolue moyenne entre les valeurs prédites et les valeurs réelles. Contrairement à MSE, MAE n'élève pas les différences au carré, ce qui le rend moins sensible aux valeurs aberrantes. Par rapport à l'erreur quadratique moyenne (MSE), l'erreur absolue moyenne (MAE) est intrinsèquement moins sensible aux valeurs aberrantes, car elle attribue un poids égal à toutes les erreurs, quelle que soit leur ampleur.
Cela signifie que si une valeur aberrante peut fausser de manière significative l'EQM en contribuant à une erreur disproportionnée lorsqu'elle est élevée au carré, son impact sur l'EQM est beaucoup plus limité. L'influence d'une valeur aberrante sur la métrique d'erreur globale est minime lorsque l'on utilise la MAE comme fonction de perte. En revanche, l'EQM amplifie l'effet des valeurs aberrantes en raison de la mise au carré des termes d'erreur, ce qui affecte l'estimation de l'erreur du modèle de manière plus substantielle.
Un scénario dans lequel MAE est une fonction de perte applicable est celui dans lequel nous ne voulons pas pénaliser les valeurs aberrantes de manière considérable ou pas du tout, par exemple, la prédiction des délais de livraison pour une entreprise de livraison de produits alimentaires.
Une société de services de livraison comme UberEats, Deliveroo ou DoorDash pourrait élaborer un modèle d'estimation des livraisons afin d'accroître la satisfaction des clients. Le temps nécessaire à un service de livraison pour acheminer des denrées alimentaires dépend de plusieurs facteurs tels que les conditions météorologiques, les incidents de circulation, les travaux routiers, etc.
Le traitement de ces facteurs est crucial pour l'estimation des délais de livraison. L'une des méthodes consiste à classer ces événements comme des valeurs aberrantes, mais à prendre la décision de s'assurer qu'ils n'affectent pas le modèle en cours d'apprentissage. La MAE est une fonction de perte appropriée dans ce scénario, car elle traite les points de données aberrants dus à des travaux routiers ou à des événements rares avec moins de sévérité, ce qui réduit l'effet des aberrations sur la métrique d'erreur et le processus d'apprentissage du modèle.
L'EAM ajoute notamment une pondération d'erreur uniforme à tous les points de données ; dans le scénario décrit, la pénalisation des points de données aberrants pourrait entraîner une surestimation ou une sous-estimation des délais de livraison.
Perte de Huber / Erreur absolue moyenne lisse
La perte de Huber ou erreur absolue moyenne lisse est une fonction de perte qui reprend les caractéristiques avantageuses des fonctions de perte erreur absolue moyenne et erreur quadratique moyenne et les combine en une seule fonction de perte. La nature hybride de la perte de Huber la rend moins sensible aux valeurs aberrantes, tout comme la MAE, mais pénalise également les erreurs mineures au sein de l'échantillon de données, tout comme la MSE. La fonction de perte de Huber est également utilisée dans les tâches d'apprentissage automatique de la régression.
L'équation mathématique de la perte de Huber est la suivante :
L(δ, y, f(x)) = (1/2) * (f(x) - y)^2 if |f(x) - y| <= δ
= δ * |f(x) - y| - (1/2) * δ^2 if |f(x) - y| > δOù ?
- L représente la fonction de perte de Huber
- δ est le paramètre delta, qui détermine le seuil de commutation entre les composantes quadratique et linéaire de la fonction de perte.
- y est la valeur réelle ou la valeur cible
- f(x) est la valeur prédite
Quand utiliser la perte de Huber / l'erreur absolue moyenne lisse ?
La fonction de perte de Huber combine effectivement deux composantes pour traiter les erreurs différemment, le point de transition entre ces composantes étant déterminé par le seuil δ :
- Composante quadratique pour les petites erreurs : Pour les erreurs inférieures à δ, il utilise la composante quadratique
(1/2) * (f(x) - y)^2 - Composante linéaire pour les erreurs importantes : Pour les erreurs supérieures à δ, il applique la composante linéaire
δ * |f(x) - y| - (1/2) * δ^2
La perte de Huber fonctionne selon deux modes qui sont commutés en fonction de l'importance de la différence calculée entre la valeur cible réelle et la prédiction de l'algorithme d'apprentissage automatique. Le terme clé de la perte de Huber est le delta (δ). Le delta est un seuil qui détermine la limite numérique à partir de laquelle la perte de Huber utilise l'application quadratique de la perte ou le calcul linéaire.
La composante quadratique de la perte de Huber caractérise les avantages de l'EQM qui pénalise les valeurs aberrantes ; dans le cadre de la perte de Huber, elle s'applique aux erreurs inférieures au delta, ce qui garantit une prédiction plus précise du modèle.
Supposons que l'erreur calculée, qui est la différence entre les valeurs réelles et prédites, soit supérieure au delta. Dans ce cas, la perte de Huber utilise le calcul linéaire de la perte similaire au MAE, où la sensibilité à la taille de l'erreur est moindre pour s'assurer que le modèle formé ne pénalise pas trop les erreurs importantes, en particulier si l'ensemble de données contient des valeurs aberrantes ou des échantillons de données peu susceptibles de se produire.
Fonctions de perte pour la classification
Perte d'entropie croisée binaire / Perte logarithmique
La perte d'entropie croisée binaire (BCE) est une mesure de performance pour les modèles de classification qui produit une prédiction avec une valeur de probabilité généralement comprise entre 0 et 1, et cette valeur de prédiction correspond à la probabilité qu'un échantillon de données appartienne à une classe ou à une catégorie. Dans le cas de la perte d'entropie croisée binaire, il existe deux classes distinctes. Mais surtout, une variante de la perte d'entropie croisée, l'entropie croisée catégorielle, s'applique aux scénarios de classification multiclasse.
Pour comprendre la perte d'entropie croisée binaire, parfois appelée perte logarithmique, il est utile d'examiner les composantes des termes.
- Perte: Il s'agit d'une quantification mathématique de la marge/différence entre la prédiction d'un algorithme d'apprentissage automatique et la valeur cible réelle.
- Entropie: Une définition simple de l'entropie est qu'il s'agit d'un calcul du degré d'aléatoire ou de désordre au sein d'un système
- Entropie croisée: Il s'agit d'un terme couramment utilisé dans la théorie de l'information, qui mesure les différences entre deux distributions de probabilité pouvant être utilisées pour identifier une observation.
- Binaire: Il s'agit d'une expression de chiffres numériques utilisant l'un des deux états, 0 ou 1. Ce principe est étendu à la définition de la classification binaire, dans laquelle nous définissons deux classes (A et B) à l'aide d'une représentation binaire, la classe A étant représentée numériquement par 0 et la classe B par 1.
La perte d'entropie croisée binaire (ou perte logarithmique) est une quantification de la différence entre la prédiction d'un algorithme d'apprentissage automatique et la prédiction cible réelle, calculée à partir de la valeur négative de la sommation de la valeur logarithmique des probabilités des prédictions faites par l'algorithme d'apprentissage automatique par rapport au nombre total d'échantillons de données. BCE se retrouve dans les cas d'utilisation de l'apprentissage automatique qui sont des problèmes de régression logistique et dans la formation de réseaux neuronaux artificiels conçus pour prédire la probabilité qu'un échantillon de données appartienne à une classe et pour exploiter la fonction d'activation sigmoïde en interne.
L'équation mathématique de la perte d'entropie croisée binaire, également connue sous le nom de perte logarithmique, est la suivante :
L(y, f(x)) = -[y * log(f(x)) + (1 - y) * log(1 - f(x))]Où ?
- L représente la fonction de perte de l'entropie croisée binaire.
- y est la véritable étiquette binaire (0 ou 1)
- f(x) est la probabilité prédite de la classe positive (entre 0 et 1)
Quand utiliser la perte d'entropie croisée binaire / la perte logarithmique ?
L'équation ci-dessus s'applique spécifiquement à un scénario dans lequel l'algorithme d'apprentissage automatique effectue une classification entre deux classes. Il s'agit d'un scénario de classification binaire.
Comme indiqué dans l'équation par le symbole négatif : BCE calcule la perte en déterminant la valeur négative de deux termes et, pour plusieurs prédictions ou échantillons de données, la moyenne de la valeur négative des deux termes suivants :
- Le logarithme de la probabilité prédite par le modèle que la classe positive soit présente y * log(f(x))
- Le logarithme de 1 moins la probabilité prédite de la classe négative : (1 - y) * log(1 - f(x))
La fonction de perte BCE pénalise les prédictions inexactes, c'est-à-dire les prédictions qui présentent une différence significative par rapport à la classe positive ou, en d'autres termes, qui ont une quantification élevée de l'entropie. Lorsque BCE est utilisé comme composant dans les algorithmes d'apprentissage, cela encourage le modèle à affiner ses prédictions, qui sont des probabilités pour la classe appropriée au cours de sa formation.
Perte de charnière
La perte de charnière est une fonction de perte utilisée dans l'apprentissage automatique pour former des classificateurs qui optimisent l'augmentation de la marge entre les points de données et la limite de décision. Il est donc principalement utilisé pour les classifications à marge maximale. Pour garantir une marge maximale entre les points de données et les limites, la perte de charnière pénalise les prédictions du modèle d'apprentissage automatique qui sont mal classées, c'est-à-dire les prédictions qui se situent du mauvais côté de la limite de la marge, ainsi que les prédictions qui sont correctement classées mais qui se trouvent à proximité de la limite de décision.
Cette caractéristique de la fonction de perte charnière garantit que les modèles d'apprentissage automatique sont capables de prédire la classification précise des points de données à leur valeur cible avec une confiance qui dépasse le seuil de la limite de décision. Cette approche de l'apprentissage automatique des algorithmes améliore les capacités de généralisation du modèle, ce qui le rend efficace pour classer avec précision des points de données avec un degré élevé de certitude.
L'équation mathématique de la perte de charnière est la suivante :
L(y, f(x)) = max(0, 1 - y * f(x))Où ?
- L représente la perte de la charnière
- y est la véritable étiquette ou la valeur cible (-1 ou 1)
- f(x) est la valeur prédite ou la sortie de la fonction de décision
Choisir la bonne fonction de perte
Il est essentiel de sélectionner la fonction de perte appropriée à appliquer à un algorithme d'apprentissage automatique, car les performances du modèle dépendent fortement de la capacité de l'algorithme à apprendre ou à adapter ses poids internes pour s'adapter à un ensemble de données.
La performance d'un modèle ou d'un algorithme d'apprentissage automatique est définie par la fonction de perte utilisée, principalement parce que la composante de la fonction de perte affecte l'algorithme d'apprentissage utilisé pour minimiser la perte d'erreur du modèle ou la valeur de la fonction de coût. Essentiellement, la fonction de perte a un impact sur la capacité du modèle à apprendre et à adapter la valeur de ses poids internes pour s'adapter aux modèles d'un ensemble de données.
Lorsqu'elle est correctement sélectionnée, la fonction de perte permet à l'algorithme d'apprentissage de converger efficacement vers une perte optimale au cours de sa phase d'apprentissage et de bien se généraliser à des échantillons de données non vus. Une fonction de perte correctement sélectionnée agit comme un guide, orientant l'algorithme d'apprentissage vers la précision et la fiabilité, en veillant à ce qu'il capture les modèles sous-jacents dans les données tout en évitant l'ajustement excessif ou insuffisant.
Facteurs à prendre en compte lors de la sélection d'une fonction de perte
Comprendre le type de problème d'apprentissage automatique à résoudre permet de déterminer la catégorie de fonction de perte à utiliser. Différentes fonctions de perte s'appliquent à divers problèmes d'apprentissage automatique.
Classification et régression
Les tâches d'apprentissage automatique de la classification impliquent généralement l'affectation de points de données à une catégorie spécifique. Dans ce type de tâche d'apprentissage automatique, le résultat du modèle d'apprentissage automatique est généralement un ensemble de probabilités qui déterminent la probabilité qu'un point de données corresponde à une certaine étiquette.
La fonction de perte d'entropie croisée est couramment utilisée pour les tâches de classification. Dans une tâche de régression d'apprentissage automatique où l'objectif est qu'un modèle d'apprentissage automatique produise une prédiction sur la base d'un ensemble d'entrées, les fonctions de perte telles que l'erreur quadratique moyenne ou l'erreur absolue moyenne sont mieux adaptées.
Classification binaire ou multiclasse
La classification binaire consiste à classer les échantillons de données dans deux catégories distinctes, tandis que la classification multiclasse, comme son nom l'indique, consiste à classer les échantillons de données dans plus de deux catégories. Pour les problèmes de classification de l'apprentissage automatique qui ne comportent que deux classes (classification binaire), il est préférable d'utiliser une fonction de perte d'entropie croisée binaire. Dans les situations où plus de deux classes sont visées par les prédictions, il convient d'utiliser l'entropie croisée catégorielle.
Sensibilité
Un autre facteur à prendre en compte est la sensibilité de la fonction de perte aux valeurs aberrantes. Dans certains cas, il est souhaitable de s'assurer que les valeurs aberrantes et les échantillons de données qui faussent la distribution statistique globale de l'ensemble de données sont pénalisés pendant l'apprentissage ; dans ce cas, les fonctions de perte telles que l'erreur quadratique moyenne sont appropriées.
Dans certains scénarios, il est nécessaire d'être moins sensible aux valeurs aberrantes, mais il s'agit de scénarios dans lesquels les valeurs aberrantes ne se produisent jamais ou ne sont pas susceptibles de se produire. Pour cet objectif, la pénalisation des valeurs aberrantes pourrait produire un modèle non performant. La fonction de perte telle que l'erreur absolue moyenne est applicable dans de tels scénarios. Pour obtenir le meilleur des deux mondes, les praticiens devraient envisager la fonction de perte de Huber, dont les composantes pénalisent les valeurs aberrantes avec de faibles valeurs d'erreur et réduisent la sensibilité du modèle aux valeurs aberrantes avec de grandes valeurs d'erreur.
Efficacité informatique
Les ressources informatiques sont une marchandise dans le domaine de l'apprentissage automatique, du commerce et de la recherche. L'accès à une grande capacité de calcul permet aux praticiens d'expérimenter avec de grands ensembles de données et de résoudre des problèmes d'apprentissage automatique plus complexes. Certaines fonctions de perte sont plus exigeantes que d'autres en termes de calcul, en particulier lorsque le nombre d'ensembles de données est élevé. L'efficacité de calcul d'une fonction de perte est donc un facteur à prendre en compte lors du processus de sélection d'une fonction de perte.
|
Facteur |
Description |
|
Type de problème d'apprentissage |
Classification et régression ; classification binaire et multiclasse. |
|
Sensibilité du modèle aux valeurs aberrantes |
Certaines fonctions de perte sont plus sensibles aux valeurs aberrantes (par exemple, MSE), tandis que d'autres sont plus robustes (par exemple, MAE). |
|
Comportement modèle souhaité |
Influence le comportement du modèle, par exemple, la perte de charnière dans les SVM se concentre sur la maximisation de la marge. |
|
Efficacité du calcul |
Certaines fonctions de perte sont plus exigeantes en termes de calcul, ce qui influe sur le choix en fonction des ressources disponibles. |
|
Propriétés de Convergence |
La douceur et la convexité d'une fonction de perte peuvent influer sur la facilité et la rapidité de l'apprentissage. |
|
L'ampleur de la tâche |
Pour les tâches à grande échelle, il est essentiel de disposer d'une fonction de perte qui s'adapte bien et qui peut être optimisée efficacement. |
Impact des valeurs aberrantes et de la distribution des données
Les valeurs aberrantes sont des échantillons de données qui sortent de la distribution statistique globale d'un ensemble de données ; elles sont parfois appelées anomalies ou irrégularités. La façon dont les valeurs aberrantes sont gérées détermine la performance et la précision du modèle d'apprentissage automatique formé.
Comme indiqué précédemment, les valeurs aberrantes dans les ensembles de données affectent les valeurs d'erreur utilisées dans les fonctions de perte, en fonction de la fonction de perte utilisée. L'effet des valeurs aberrantes sur les fonctions de perte se propage au résultat du processus d'apprentissage de l'algorithme d'apprentissage automatique, ce qui peut entraîner un comportement intentionnel ou non de l'algorithme ou du modèle d'apprentissage automatique.
Par exemple, l'erreur quadratique moyenne pénalise les valeurs aberrantes qui contribuent à des valeurs/termes d'erreur élevés ; cela signifie que, pendant le processus de formation, les poids du modèle sont ajustés pour apprendre à tenir compte de ces valeurs aberrantes. Là encore, s'il ne s'agit pas du comportement prévu du modèle d'apprentissage automatique, le modèle finalisé créé après la formation présentera une faible généralisation aux données inédites. Pour les scénarios où il est nécessaire d'atténuer l'impact des valeurs aberrantes, des fonctions telles que le MAE et la perte de Huber sont plus adaptées.
|
Fonction de perte |
Applicabilité à la classification |
Applicabilité à la régression |
Sensibilité aux valeurs aberrantes |
|
Erreur quadratique moyenne (EQM) |
✖️ |
✔️ |
Haut |
|
Erreur absolue moyenne (MAE) |
✖️ |
✔️ |
Faible |
|
Entropie croisée |
✔️ |
✖️ |
Moyen |
|
Perte de charnière |
✔️ |
✖️ |
Faible |
|
Perte de Huber |
✖️ |
✔️ |
Moyen |
|
Perte de logs |
✔️ |
✖️ |
Moyen |
Mise en œuvre des fonctions de perte
Exemples de mise en œuvre de fonctions de perte courantes
Mise en œuvre de MAE en Python
# Python implementation of Mean Absolute Error (MAE)
def mean_absolute_error(actual:list, predicted:list) -> float:
"""
Calculate the Mean Absolute Error between actual and predicted values
:param actual: list, actual values
:param predicted: list, predicted values
:return: float, the calculated MAE
"""
# Ensure the length of the two lists are the same
if len(actual) != len(predicted):
raise ValueError("The length of actual values and predicted values must be the same")
# Calculate the absolute differences
absolute_diffs = [abs(act - pred) for act, pred in zip(actual, predicted)]
# Calculate the mean of the absolute differences
mae = sum(absolute_diffs) / len(actual)
return mae
# Example usage:
# actual values
y_true = [3, -0.5, 2, 7]
# predicted values
y_pred = [2.5, 0.0, 2, 8]
# Calculate MAE
mae_value = mean_absolute_error(y_true, y_pred)
print(mae_value)
# 0.5Mise en œuvre de l'ESM en Python
# Python implementation of Mean Squared Error (MSE) / L2 Loss
def mean_squared_error(actual:list, predicted:list) -> float:
"""
Calculate the Mean Squared Error between actual and predicted values
:param actual: list, actual values
:param predicted: list ,predicted values
:return: float, the calculated MSE
"""
# Ensure the length of the two lists are the same
if len(actual) != len(predicted):
raise ValueError("The length of actual values and predicted values must be the same")
# Calculate the squared differences
# (yᵢ - ȳ)²
squared_diffs = [(act - pred) ** 2 for act, pred in zip(actual, predicted)]
# Calculate the mean of the squared differences
mse = sum(squared_diffs) / len(actual)
return mse
# Example usage:
# actual values
y_true = [1, 2, 3, 4, 5]
# predicted values
y_pred = [1.1, 2.2, 2.9, 4.1, 4.9]
# Calculate MSE
mse_value = mean_squared_error(y_true, y_pred)
print(mse_value)
# 0.015999999999999993L'utilisation de bibliothèques pour la mise en œuvre de fonctions de perte
Bien qu'il soit possible de personnaliser l'implémentation des fonctions de perte et que les bibliothèques d'apprentissage profond telles que TensorFlow et PyTorch prennent en charge l'utilisation de fonctions de perte personnalisées dans les implémentations de réseaux neuronaux, des bibliothèques telles que Scikit-learn, TensorFlow et PyTorch proposent des implémentations intégrées de fonctions de perte couramment utilisées.
Ces fonctionnalités pré-intégrées facilitent l'exploitation et éliminent les complexités liées à la mise en œuvre de ces fonctions de perte, rationalisant ainsi le processus de développement des modèles d'apprentissage automatique.
L'utilisation de ces bibliothèques d'apprentissage profond présente des avantages par rapport aux implémentations purement Python, dont certains sont les suivants :
- Facilité d'utilisation
- Efficacité et optimisation
- Prise en charge de l'informatique parallèle et du GPU
- Soutien à la communauté des développeurs
Erreur absolue moyenne (MAE) à l'aide de la bibliothèque scikit-learn
from sklearn.metrics import mean_absolute_error
# actual values
y_true = [3, -0.5, 2, 7]
# predicted values
y_pred = [2.5, 0.0, 2, 8]
# Calculate MAE using scikit-learn
mae_value = mean_absolute_error(y_true, y_pred)
print(mae_value)
#0.5Erreur quadratique moyenne (EQM) à l'aide de la bibliothèque scikit-learn
from sklearn.metrics import mean_squared_error
# actual values
y_true = [1, 2, 3, 4, 5]
# predicted values
y_pred = [1.1, 2.2, 2.9, 4.1, 4.9]
# Calculate MSE using scikit-learn
mse_value = mean_squared_error(y_true, y_pred)
print(mse_value)
# 0.016Conclusion
En résumé, le choix de la bonne fonction de perte est crucial pour une formation efficace des modèles d'apprentissage automatique. Cet article présente les principales fonctions de perte, leur rôle dans les algorithmes d'apprentissage automatique et leur adéquation à différentes tâches. De l'erreur quadratique moyenne (MSE) à la perte de Huber, chaque fonction présente des avantages uniques, qu'il s'agisse de traiter les valeurs aberrantes ou d'équilibrer le biais et la variance.
La décision d'utiliser des fonctions de perte personnalisées ou préconstruites à partir de bibliothèques telles que Scikit-learn, TensorFlow et PyTorch dépend des besoins spécifiques du projet, de l'efficacité de calcul et de l'expertise de l'utilisateur. Ces bibliothèques offrent une grande facilité de mise en œuvre, un soutien continu de la communauté et des mises à jour régulières.
Malgré l'évolution de l'apprentissage automatique, l'importance des fonctions de perte reste constante. Les tendances futures peuvent apporter des fonctions de perte plus spécialisées, mais les principes fondamentaux persisteront probablement. Pour une plongée plus profonde dans l'apprentissage automatique et ses applications, explorez la piste Machine Learning Scientist with Python de DataCamp.