Explicação das funções de perda no aprendizado de máquina

O aprendizado de máquina fornece modelos computacionais com a capacidade de fazer previsões, classificações e decisões com base em dados. Como um campo de estudo, o aprendizado de máquina é um subconjunto do domínio da inteligência artificial, que engloba os processos envolvidos na criação de um modelo computacional com recursos que imitam a inteligência humana e, em alguns casos, a superam.

O aprendizado de máquina e os algoritmos e técnicas associados envolvem fundamentalmente o projeto, a implementação e o treinamento de algoritmos para reconhecer padrões em dados expostos e realizar previsões ou classificações.

Os algoritmos de aprendizado de máquina aprendem por meio de diferentes métodos, mas um componente fundamental do processo de aprendizado dos algoritmos e modelos de aprendizado de máquina é a função de perda. A função de perda é um processo matemático que quantifica a margem de erro entre a previsão de um modelo e o valor-alvo real. Mais adiante neste artigo, exploraremos a função de perda em detalhes.

Funções de perda em resumo

A principal conclusão é que a função de perda é uma forma mensurável de avaliar o desempenho e a precisão de um modelo de aprendizado de máquina. Nesse caso, a função de perda atua como um guia para o processo de aprendizado em um modelo ou algoritmo de aprendizado de máquina.

O papel da função de perda é crucial no treinamento de modelos de aprendizado de máquina e inclui o seguinte:

• Medição de desempenho: As funções de perda oferecem uma métrica clara para avaliar o desempenho de um modelo, quantificando a diferença entre as previsões e os resultados reais.
• Direção para aprimoramento: As funções de perda orientam o aprimoramento do modelo, direcionando o algoritmo para ajustar os parâmetros (pesos) iterativamente para reduzir a perda e melhorar as previsões.
• Equilibrar a tendência e a variação: Funções de perda eficazes ajudam a equilibrar a tendência do modelo (simplificação excessiva) e a variância (ajuste excessivo), o que é essencial para a generalização do modelo para novos dados.
• Influenciando o comportamento do modelo: Determinadas funções de perda podem afetar o comportamento do modelo, como ser mais robusto em relação a outliers de dados ou priorizar tipos específicos de erros.

Vamos explorar os papéis de funções de perda específicas em seções posteriores e criar uma intuição e um entendimento detalhados da função de perda.

O que é uma função de perda?

A função de perda, também chamada de função de erro, é um componente crucial no aprendizado de máquina que quantifica a diferença entre as saídas previstas de um algoritmo de aprendizado de máquina e os valores-alvo reais. Por exemplo, em um problema de regressão para prever preços de carros com base em dados históricos, uma função de perda avalia uma previsão de rede neural com base em uma amostra de treinamento do conjunto de dados de treinamento. A função de perda quantifica a diferença ou a margem de erro entre o preço do carro previsto pela rede e o preço real.

O valor resultante, a perda, reflete a precisão das previsões do modelo. Durante o treinamento, um algoritmo de aprendizado, como o algoritmo de retropropagação, usa o gradiente da função de perda em relação aos parâmetros do modelo para ajustar esses parâmetros e minimizar a perda, melhorando efetivamente o desempenho do modelo no conjunto de dados.

Frequentemente, os termos função de perda e função de custo são usados de forma intercambiável; apesar disso, ambos os termos têm definições distintas:

Conforme mencionado anteriormente, a função de perda, também conhecida como função de erro, quantifica a qualidade de uma única previsão do algoritmo de aprendizado de máquina em comparação com o valor-alvo real. A principal conclusão é que uma função de perda se aplica a um único exemplo de treinamento e faz parte do processo geral de aprendizado do modelo que fornece o sinal pelo qual o algoritmo de aprendizado do modelo atualiza os pesos e os parâmetros.

A função de custo, às vezes chamada de função objetiva, é uma média da função de perda de todo um conjunto de treinamento que contém vários exemplos de treinamento. A função de custo quantifica o desempenho do modelo em todo o conjunto de dados de treinamento.

Vamos nos aprofundar em como funcionam as funções de perda.

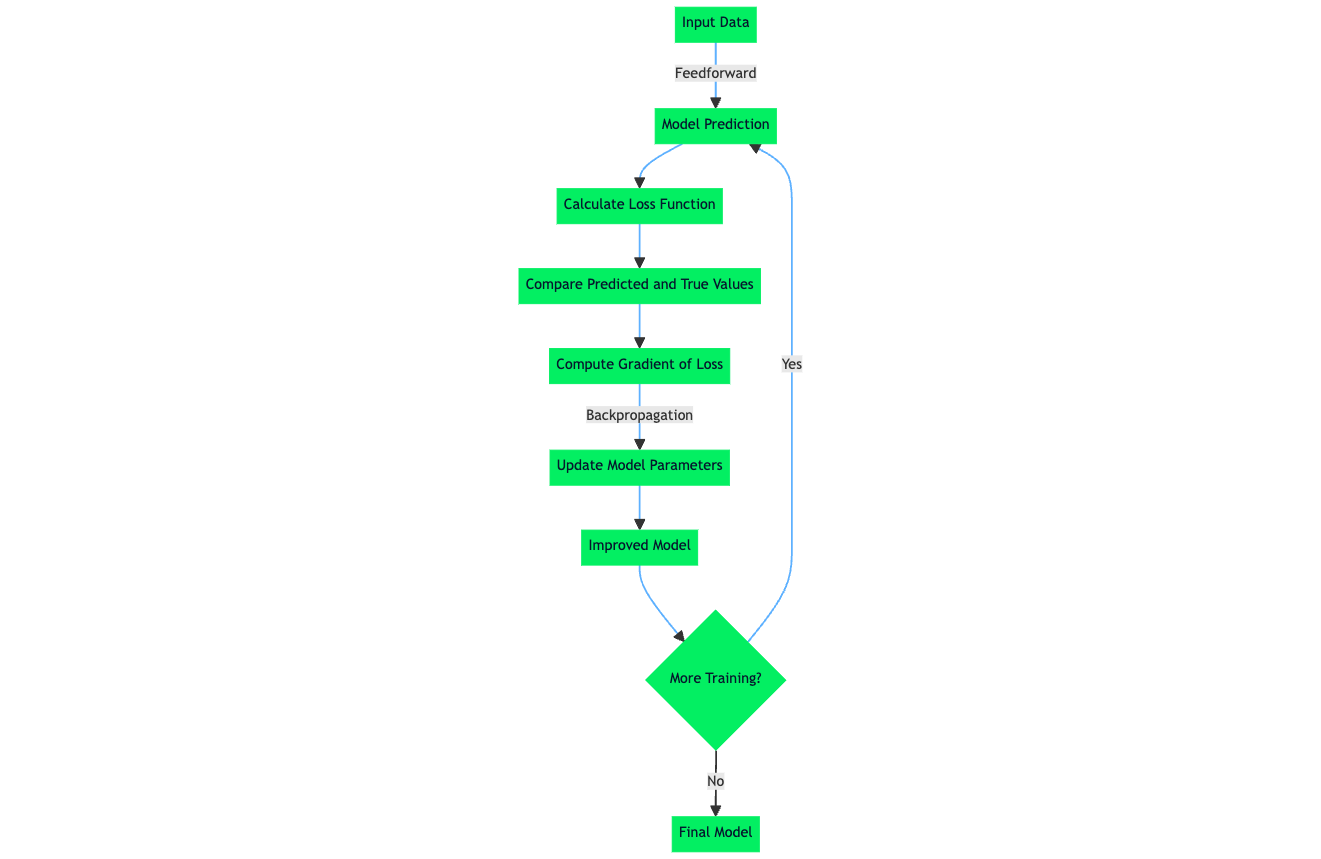
Como funcionam as funções de perda

Embora existam diferentes tipos de funções de perda, fundamentalmente, todas elas operam quantificando a diferença entre as previsões de um modo e o valor-alvo real no conjunto de dados. O termo oficial para essa quantificação numérica é o erro de previsão. O algoritmo e os mecanismos de aprendizado em um modelo de aprendizado de máquina são otimizados para minimizar o erro de previsão, o que significa que, após um cálculo do valor da função de perda, que é determinado pelo erro de previsão, o algoritmo de aprendizado aproveita essas informações para realizar atualizações de pesos e parâmetros que, na verdade, durante a próxima passagem de treinamento, levam a um erro de previsão menor.

Ao explorar o tópico de função de perda, algoritmos de aprendizado de máquina e o processo de aprendizado em redes neurais, surge o tópico de Empirical Risk Minimization (ERM). O ERM é uma abordagem para selecionar os parâmetros ideais de um algoritmo de aprendizado de máquina que minimiza o risco empírico. O risco empírico, nesse caso, é o conjunto de dados de treinamento.

O componente de minimização de risco do ERM é o processo pelo qual o algoritmo de aprendizado interno minimiza o erro de previsão do algoritmo de aprendizado de máquina para um conjunto de dados conhecido, de modo que o modelo tenha um desempenho e uma precisão esperados em um cenário em que um conjunto de dados ou uma amostra de dados não vistos possam ter uma distribuição de dados estática semelhante à do conjunto de dados no qual o modelo foi inicialmente treinado.

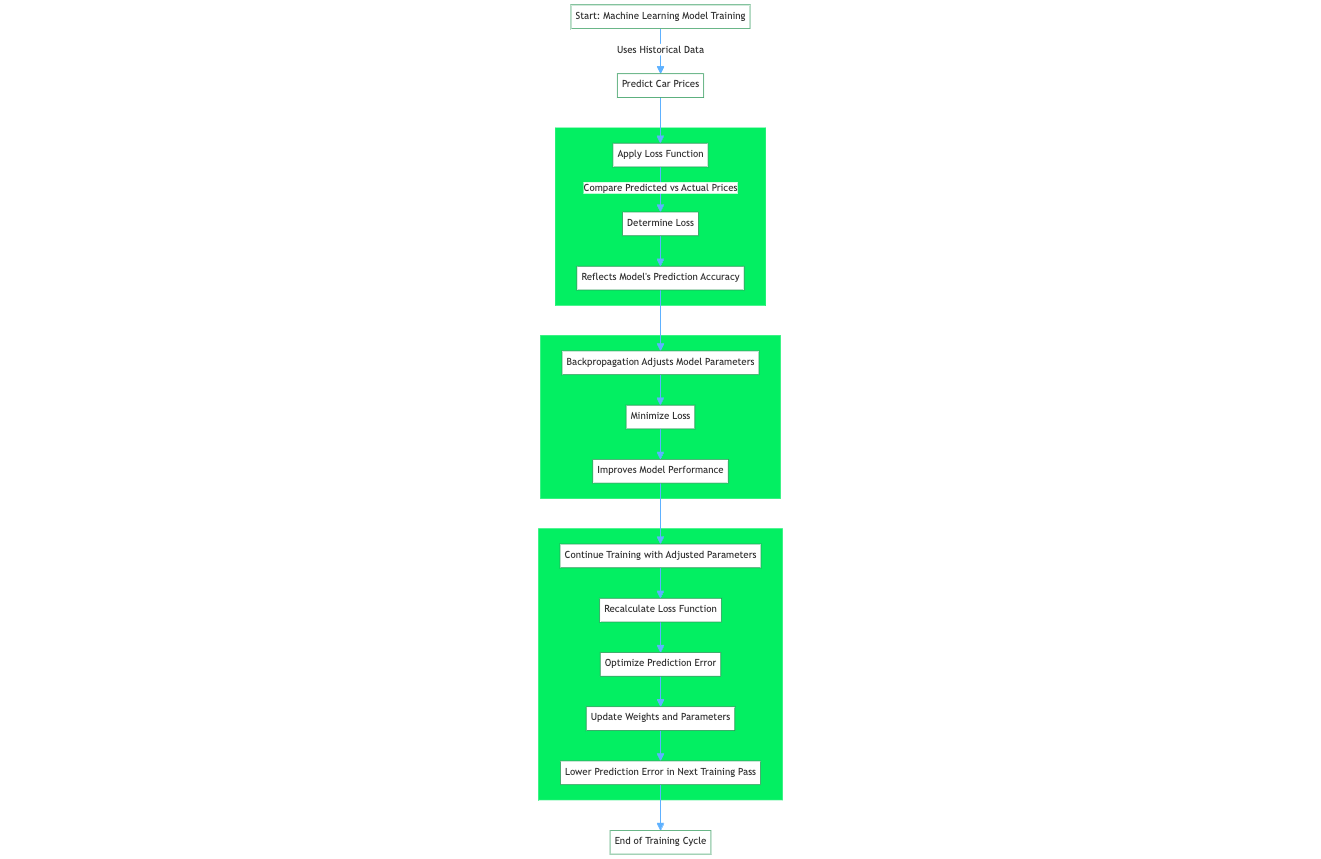
Tipos de funções de perda

As funções de perda no aprendizado de máquina podem ser categorizadas com base nas tarefas de aprendizado de máquina às quais são aplicáveis. A maioria das funções de perda se aplica a problemas de aprendizado de máquina de regressão e classificação. Espera-se que o modelo preveja valores de saída contínuos para tarefas de aprendizado de máquina de regressão. Em contrapartida, espera-se que o modelo forneça rótulos discretos correspondentes a uma classe de conjunto de dados para tarefas de classificação.

Abaixo estão as funções de perda padrão e sua classificação em problemas de aprendizado de máquina aos quais elas se prestam bem. A maioria dessas funções de perda é abordada em detalhes mais adiante neste artigo.

Funções de perda para regressão

Erro Quadrático Médio (MSE) / Perda L2

O erro quadrático médio (MSE) ou perda L2 é uma função de perda que quantifica a magnitude do erro entre a previsão de um algoritmo de aprendizado de máquina e uma saída real, considerando a média da diferença quadrada entre as previsões e os valores-alvo. O quadrado da diferença entre as previsões e os valores-alvo reais resulta em uma penalidade maior atribuída a desvios mais significativos do valor-alvo. Uma média dos erros normaliza o total de erros em relação ao número de amostras em um conjunto de dados ou observação.

A equação matemática do erro quadrático médio (MSE) ou perda L2 é:

MSE = (1/n) * Σ(yᵢ - ȳ)²

Onde:

• n é o número de amostras no conjunto de dados
• yᵢ é o valor previsto para a i-ésima amostra
• ȳ é o valor-alvo para a i-ésima amostra

Quando usar o MSE

Entender quando usar o MSE é fundamental no desenvolvimento de modelos de aprendizado de máquina. O MSE é uma função de perda padrão utilizada na maioria das tarefas de regressão, pois direciona o modelo a ser otimizado para minimizar as diferenças quadráticas entre os valores previstos e os valores-alvo.

O MSE é recomendado para cenários de ML em que é favorável ao processo de aprendizado penalizar significativamente a presença de outliers. No entanto, essas características do MSE nem sempre são adequadas para cenários e casos de uso em que os valores discrepantes se devem ao ruído dos dados, em vez de sinais positivos.

Um exemplo de cenário em que a função de perda MSE é aproveitada é a previsão de preços de imóveis ou, de forma mais ampla, a modelagem preditiva. A previsão de preços de imóveis envolve o uso de características como número de cômodos, localização, área, distância das comodidades e outras características numéricas. Os preços das casas em uma área localizada são normalmente distribuídos, portanto, o objetivo de penalizar os outliers é essencial para a capacidade do modelo de prever preços de casas precisos.

Um pequeno erro percentual no setor imobiliário pode equivaler a uma quantia significativa de dinheiro. Por exemplo, um erro de 5% em uma casa de US$ 200.000 é de US$ 10.000, o que é substancial. Portanto, elevar os erros ao quadrado (como é feito no MSE) ajuda a dar maior peso aos erros maiores, fazendo com que o modelo seja mais preciso com propriedades de valor mais alto.

Erro Absoluto Médio (MAE) / Perda L1

O erro absoluto médio (MAE), também conhecido como perda L1, é uma função de perda usada em tarefas de regressão que calcula as diferenças absolutas médias entre os valores previstos de um modelo de aprendizado de máquina e os valores-alvo reais. Ao contrário do erro quadrático médio (MSE), o MAE não eleva as diferenças ao quadrado, tratando todos os erros com o mesmo peso, independentemente de sua magnitude.

A equação matemática do erro absoluto médio (MAE) ou perda L1 é:

MAE = (1/n) * Σ|yᵢ - ȳ|

Onde:

• n é o número de amostras no conjunto de dados
• yᵢ é o valor previsto para a i-ésima amostra
• ȳ é o valor-alvo para a i-ésima amostra

Quando usar o MAE

O MAE mede a diferença média absoluta entre os valores previstos e os valores reais. Ao contrário do MSE, o MAE não eleva as diferenças ao quadrado, o que o torna menos sensível a valores discrepantes. Em comparação com o erro quadrático médio (MSE), o erro absoluto médio (MAE) é inerentemente menos sensível a outliers porque atribui um peso igual a todos os erros, independentemente de sua magnitude.

Isso significa que, embora um outlier possa distorcer significativamente o MSE, contribuindo com um erro desproporcionalmente grande quando elevado ao quadrado, seu impacto no MAE é muito mais contido. A influência de um outlier na métrica de erro geral é mínima quando se usa o MAE como uma função de perda. Por outro lado, o MSE amplifica o efeito dos outliers devido ao quadrado dos termos de erro, afetando mais substancialmente a estimativa de erro do modelo.

Um cenário em que o MAE é uma função de perda aplicável é aquele em que não queremos penalizar os outliers consideravelmente ou de forma alguma, por exemplo, prever os tempos de entrega para uma empresa de entrega de alimentos.

Uma empresa de serviços de entrega, como UberEats, Deliveroo ou DoorDash, pode criar um modelo de estimativa de entrega para aumentar a satisfação do cliente. O tempo que um serviço de entrega leva para entregar os alimentos é afetado por vários fatores, como clima, incidentes de trânsito, obras na estrada etc.

O manuseio desses fatores é fundamental para a estimativa dos prazos de entrega. Um método de lidar com isso é classificar esses eventos como discrepantes, mas tomar a decisão de garantir que não afetem o modelo que está sendo treinado. O MAE é uma função de perda adequada nesse cenário, pois tratará os pontos de dados que são discrepantes devido a obras na estrada ou eventos raros com menos gravidade, reduzindo o efeito dos discrepantes na métrica de erro e no processo de aprendizado do modelo.

O MAE adiciona, notavelmente, uma ponderação de erro uniforme a todos os pontos de dados; no cenário descrito, a penalização de pontos de dados discrepantes poderia resultar em uma superestimação ou subestimação dos tempos de entrega.

Perda de Huber / Erro Absoluto Médio Suave

A perda de Huber ou Smooth Mean Absolute Error é uma função de perda que utiliza as características vantajosas das funções de perda Mean Absolute Error e Mean Squared Error e as combina em uma única função de perda. A natureza híbrida da Perda de Huber faz com que ela seja menos sensível a outliers, assim como o MAE, mas também penaliza erros menores dentro da amostra de dados, semelhante ao MSE. A função de perda Huber também é utilizada em tarefas de aprendizado de máquina de regressão.

A equação matemática da perda de Huber é a seguinte:

L(δ, y, f(x)) = (1/2) * (f(x) - y)^2   if |f(x) - y| <= δ
               = δ * |f(x) - y| - (1/2) * δ^2   if |f(x) - y| > δ

Onde:

• L representa a função de perda de Huber
• δ é o parâmetro delta, que determina o limite para alternar entre os componentes quadráticos e lineares da função de perda
• y é o valor real ou o valor-alvo
• f(x) é o valor previsto

Quando usar a perda de Huber / erro absoluto médio suave

A função Huber Loss combina efetivamente dois componentes para tratar os erros de forma diferente, com o ponto de transição entre esses componentes determinado pelo limite δ:

• Componente quadrático para erros pequenos: Para erros menores que δ, ele usa o componente quadrático (1/2) * (f(x) - y)^2
• Componente linear para erros grandes: Para erros maiores que δ, ele aplica o componente linear δ * |f(x) - y| - (1/2) * δ^2

A perda de Huber opera em dois modos que são alternados com base no tamanho da diferença calculada entre o valor-alvo real e a previsão do algoritmo de aprendizado de máquina. O termo-chave da perda de Huber é delta (δ). Delta é um limite que determina o limite numérico no qual a perda Huber utiliza a aplicação quadrática da perda ou o cálculo linear.

O componente quadrático da perda de Huber caracteriza as vantagens do MSE que penalizam os outliers; na perda de Huber, isso é aplicado a erros menores que delta, o que garante uma previsão mais precisa do modelo.

Suponha que o erro calculado, que é a diferença entre os valores reais e previstos, seja maior que o delta. Nesse caso, a Perda de Huber utiliza o cálculo linear de perda semelhante ao MAE, em que há menos sensibilidade ao tamanho do erro para garantir que o modelo treinado não esteja penalizando excessivamente os erros grandes, especialmente se o conjunto de dados contiver outliers ou amostras de dados improváveis de ocorrer.

Funções de perda para classificação

Perda de entropia cruzada binária / Perda de log

A perda de entropia cruzada binária (BCE) é uma medida de desempenho para modelos de classificação que produz uma previsão com um valor de probabilidade normalmente entre 0 e 1, e esse valor de previsão corresponde à probabilidade de uma amostra de dados pertencer a uma classe ou categoria. No caso da perda de entropia cruzada binária, há duas classes distintas. Mas, notavelmente, uma variante da perda de entropia cruzada, a entropia cruzada categórica, aplica-se a cenários de classificação multiclasse.

Para entender a perda de entropia cruzada binária, às vezes chamada de perda de registro, é útil discutir os componentes dos termos.

• Perda: Essa é uma quantificação matemática da margem/diferença entre a previsão de um algoritmo de aprendizado de máquina e o valor-alvo real.
• Entropia: Uma definição simples de entropia é que ela é um cálculo do grau de aleatoriedade ou desordem em um sistema
• Entropia cruzada: Esse é um termo comumente utilizado na teoria da informação e mede as diferenças entre duas distribuições de probabilidade que podem ser usadas para identificar uma observação.
• Binário: Essa é uma expressão de dígitos numéricos que usa um dos dois estados, 0 ou 1. Isso é estendido para a definição de classificação binária, em que definimos duas classes (A e B) usando representação binária, em que a classe A recebe a representação numérica 0 e a classe B recebe 1.

A perda de entropia cruzada binária (ou perda de log) é uma quantificação da diferença entre a previsão de um algoritmo de aprendizado de máquina e a previsão real do alvo, calculada a partir do valor negativo da soma do valor do logaritmo das probabilidades das previsões feitas pelo algoritmo de aprendizado de máquina em relação ao número total de amostras de dados. O BCE é encontrado em casos de uso de aprendizado de máquina que são problemas de regressão logística e no treinamento de redes neurais artificiais projetadas para prever a probabilidade de uma amostra de dados pertencer a uma classe e aproveitar a função de ativação sigmoide internamente.

A equação matemática da perda de entropia cruzada binária, também conhecida como perda de log, é:

L(y, f(x)) = -[y * log(f(x)) + (1 - y) * log(1 - f(x))]

Onde:

• L representa a função de perda de entropia cruzada binária
• y é o rótulo binário verdadeiro (0 ou 1)
• f(x) é a probabilidade prevista da classe positiva (entre 0 e 1)

Quando usar a perda de entropia cruzada binária / perda de log

A equação acima se aplica especificamente a um cenário em que o algoritmo de aprendizado de máquina fará uma classificação entre duas classes. Esse é um cenário de classificação binária.

Conforme observado na equação pelo símbolo negativo: '-', o BCE calcula a perda determinando o negativo de dois termos e, para várias previsões ou amostras de dados, a média do negativo dos dois termos seguintes:

1. O logaritmo da probabilidade prevista do modelo foi a presença da classe positiva y * log(f(x))
2. O logaritmo de 1 menos a probabilidade prevista da classe negativa: (1 - y) * log(1 - f(x))

A função de perda BCE penaliza previsões imprecisas, que são previsões que têm uma diferença significativa da classe positiva ou, em outras palavras, têm uma alta quantificação de entropia. Quando o BCE é utilizado como um componente nos algoritmos de aprendizado, isso incentiva o modelo a refinar suas previsões, que são probabilidades para a classe apropriada durante o treinamento.

Perda da dobradiça

A Perda de Hinge é uma função de perda utilizada no aprendizado de máquina para treinar classificadores que otimizam para aumentar a margem entre os pontos de dados e o limite de decisão. Por isso, ele é usado principalmente para classificações de margem máxima. Para garantir a margem máxima entre os pontos de dados e os limites, a perda de margem penaliza as previsões do modelo de aprendizado de máquina que são classificadas incorretamente, que são previsões que caem no lado errado do limite da margem, e também as previsões que são classificadas corretamente, mas estão muito próximas do limite de decisão.

Essa característica da função Hinge Loss garante que os modelos de aprendizado de máquina sejam capazes de prever a classificação precisa dos pontos de dados para seu valor-alvo com confiança que exceda o limite do limite de decisão. Essa abordagem de aprendizado de algoritmo de máquina aprimora os recursos de generalização do modelo, tornando-o eficaz para classificar com precisão os pontos de dados com um alto grau de certeza.

A equação matemática da perda da dobradiça é:

L(y, f(x)) = max(0, 1 - y * f(x))

Onde:

• L representa a perda da dobradiça
• y é o rótulo verdadeiro ou o valor-alvo (-1 ou 1)
• f(x) é o valor previsto ou o resultado da função de decisão

Escolha da função de perda correta

A seleção da função de perda adequada a ser aplicada a um algoritmo de aprendizado de máquina é essencial, pois o desempenho do modelo depende muito da capacidade do algoritmo de aprender ou adaptar seus pesos internos para se ajustar a um conjunto de dados.

O desempenho de um modelo ou algoritmo de aprendizado de máquina é definido pela função de perda utilizada, principalmente porque o componente da função de perda afeta o algoritmo de aprendizado usado para minimizar a perda de erro do modelo ou o valor da função de custo. Essencialmente, a função de perda afeta a capacidade do modelo de aprender e adaptar o valor de seus pesos internos para ajustar os padrões em um conjunto de dados.

Quando adequadamente selecionada, a função de perda permite que o algoritmo de aprendizado converse efetivamente para uma perda ideal durante a fase de treinamento e generalize bem para amostras de dados não vistas. Uma função de perda adequadamente selecionada atua como um guia, direcionando o algoritmo de aprendizado para a precisão e a confiabilidade, garantindo que ele capture os padrões subjacentes nos dados e, ao mesmo tempo, evite o excesso ou a falta de ajuste.

Fatores a serem considerados ao selecionar uma função de perda

Entender o tipo de problema de aprendizado de máquina em questão ajuda a determinar uma categoria de função de perda a ser utilizada. Diferentes funções de perda se aplicam a vários problemas de aprendizado de máquina.

Classificação vs. Regressão

As tarefas de aprendizado de máquina de classificação geralmente envolvem a atribuição de pontos de dados a um rótulo de categoria específico. Com esse tipo de tarefa de aprendizado de máquina, a saída do modelo de aprendizado de máquina é normalmente um conjunto de probabilidades que determinam a probabilidade de um ponto de dados ser um determinado rótulo.

A função de perda de entropia cruzada é comumente usada para tarefas de classificação. Em uma tarefa de regressão de aprendizado de máquina em que o objetivo é que um modelo de aprendizado de máquina produza uma previsão com base em um conjunto de entradas, as funções de perda, como o erro quadrático médio ou o erro absoluto médio, são mais adequadas.

Classificação binária vs. multiclasse

A classificação binária envolve a categorização de amostras de dados em duas categorias distintas, enquanto a classificação multiclasse, como o nome sugere, envolve a categorização de amostras de dados em mais de duas categorias. Para problemas de classificação de aprendizado de máquina que envolvem apenas duas classes (classificação binária), é melhor aproveitar uma função de perda de entropia cruzada binária. Em situações em que mais de duas classes são alvos de previsões, a entropia cruzada categórica deve ser utilizada.

Sensibilidade

Outro fator a ser considerado é a sensibilidade da função de perda aos outliers. Em alguns cenários, é desejável garantir que os outliers e as amostras de dados que distorcem a distribuição estatística geral do conjunto de dados sejam penalizados durante o treinamento; nesses cenários, as funções de perda, como o erro quadrático médio, são adequadas.

Embora existam cenários em que seja necessária menos sensibilidade aos valores atípicos, esses são cenários em que os valores atípicos podem ser "nunca eventos" ou improváveis de acontecer. Para esse objetivo, penalizar os outliers pode produzir um modelo de baixo desempenho. A função de perda, como o erro absoluto médio, é aplicável em tais cenários. Para obter o melhor dos dois mundos, os profissionais devem considerar a função de perda de Huber, que tem componentes que penalizam os outliers com valores de erro baixos e reduzem a sensibilidade do modelo aos outliers com valores de erro grandes.

Eficiência computacional

O recurso computacional é uma commodity no domínio do aprendizado de máquina, comercial e de pesquisa. O acesso à grande capacidade de computação permite que os profissionais tenham flexibilidade para fazer experiências com grandes conjuntos de dados e resolver problemas mais complexos de aprendizado de máquina. Algumas funções de perda são mais exigentes do ponto de vista computacional do que outras, especialmente quando o número de conjuntos de dados é grande. Isso faz com que a eficiência computacional de uma função de perda seja um fator a ser considerado durante o processo de seleção de uma função de perda.

Impacto dos outliers e da distribuição de dados

Os outliers são amostras de dados que estão fora da distribuição estatística geral de um conjunto de dados; às vezes são chamados de anomalias ou irregularidades. O modo como os outliers são gerenciados determina o desempenho e a precisão do modelo de aprendizado de máquina treinado.

Como mencionado anteriormente, os outliers nos conjuntos de dados afetam os valores de erro utilizados nas funções de perda, dependendo da função de perda utilizada. O efeito dos outliers nas funções de perda se propaga para o resultado do processo de aprendizado do algoritmo de aprendizado de máquina, o que pode levar a um comportamento intencional ou não intencional do algoritmo ou modelo de aprendizado de máquina.

Por exemplo, o erro quadrático médio penaliza os outliers que contribuem para grandes valores/termos de erro; isso significa que, durante o processo de treinamento, os pesos do modelo são ajustados para aprender a acomodar esses outliers. Novamente, se esse não for o comportamento pretendido do modelo de aprendizado de máquina, o modelo finalizado criado após o treinamento terá uma generalização ruim para dados não vistos. Para cenários em que é necessário atenuar o impacto dos valores discrepantes, funções como MAE e perda de Huber são mais aplicáveis.

Implementação de funções de perda

Exemplos de implementação de funções de perda comuns

Implementação do MAE em Python

# Python implementation of Mean Absolute Error (MAE)

def mean_absolute_error(actual:list, predicted:list) -> float:
    """
    Calculate the Mean Absolute Error between actual and predicted values

    :param actual: list, actual values
    :param predicted: list, predicted values
    :return: float, the calculated MAE
    """
    # Ensure the length of the two lists are the same
    if len(actual) != len(predicted):
        raise ValueError("The length of actual values and predicted values must be the same")

    # Calculate the absolute differences
    absolute_diffs = [abs(act - pred) for act, pred in zip(actual, predicted)]
    
    # Calculate the mean of the absolute differences
    mae = sum(absolute_diffs) / len(actual)
    
    return mae

# Example usage:
# actual values
y_true = [3, -0.5, 2, 7]

# predicted values
y_pred = [2.5, 0.0, 2, 8]

# Calculate MAE
mae_value = mean_absolute_error(y_true, y_pred)
print(mae_value)
# 0.5

Implementação do MSE em Python

# Python implementation of Mean Squared Error (MSE) / L2 Loss

def mean_squared_error(actual:list, predicted:list) -> float:
    """
    Calculate the Mean Squared Error between actual and predicted values

    :param actual: list, actual values
    :param predicted: list ,predicted values
    :return: float, the calculated MSE
    """
    # Ensure the length of the two lists are the same
    if len(actual) != len(predicted):
        raise ValueError("The length of actual values and predicted values must be the same")

    # Calculate the squared differences
		# (yᵢ - ȳ)²
    squared_diffs = [(act - pred) ** 2 for act, pred in zip(actual, predicted)]
    
    # Calculate the mean of the squared differences
    mse = sum(squared_diffs) / len(actual)
    
    return mse

# Example usage:
# actual values
y_true = [1, 2, 3, 4, 5]

# predicted values
y_pred = [1.1, 2.2, 2.9, 4.1, 4.9]

# Calculate MSE
mse_value = mean_squared_error(y_true, y_pred)
print(mse_value)
# 0.015999999999999993

O uso de bibliotecas para a implementação da função de perda

Embora a implementação personalizada de funções de perda seja viável, e bibliotecas de aprendizagem profunda como TensorFlow e PyTorch suportem o uso de funções de perda personalizadas em implementações de redes neurais, bibliotecas como Scikit-learn, TensorFlow e PyTorch oferecem implementações integradas de funções de perda comumente usadas.

Essas funcionalidades pré-integradas facilitam o aproveitamento e abstraem as complexidades envolvidas na implementação dessas funções de perda, simplificando o processo de desenvolvimento de modelos de aprendizado de máquina.

A utilização dessas bibliotecas de aprendizagem profunda oferece vantagens em relação às implementações puras em Python, algumas das quais são:

• Facilidade de uso
• Eficiência e otimização
• Suporte a GPU e computação paralela
• Suporte à comunidade de desenvolvedores

Erro médio absoluto (MAE) usando a biblioteca scikit-learn

from sklearn.metrics import mean_absolute_error

# actual values
y_true = [3, -0.5, 2, 7]

# predicted values
y_pred = [2.5, 0.0, 2, 8]

# Calculate MAE using scikit-learn
mae_value = mean_absolute_error(y_true, y_pred)
print(mae_value)
#0.5

Erro médio quadrático (MSE) usando a biblioteca scikit-learn

from sklearn.metrics import mean_squared_error

# actual values
y_true = [1, 2, 3, 4, 5]

# predicted values
y_pred = [1.1, 2.2, 2.9, 4.1, 4.9]

# Calculate MSE using scikit-learn
mse_value = mean_squared_error(y_true, y_pred)
print(mse_value)
# 0.016

Conclusão

Em resumo, a escolha da função de perda correta é fundamental para o treinamento eficaz do modelo de aprendizado de máquina. Este artigo destacou as principais funções de perda, suas funções nos algoritmos de aprendizado de máquina e sua adequação a diferentes tarefas. Do erro médio quadrático (MSE) à perda de Huber, cada função tem suas vantagens exclusivas, seja para lidar com outliers ou equilibrar a tendência e a variação.

A decisão de usar funções de perda personalizadas ou pré-criadas de bibliotecas como Scikit-learn, TensorFlow e PyTorch depende das necessidades específicas do projeto, da eficiência computacional e da experiência do usuário. Essas bibliotecas oferecem facilidade de implementação, suporte contínuo da comunidade e atualizações regulares.

Apesar da evolução do aprendizado de máquina, a importância das funções de perda permanece constante. As tendências futuras podem trazer funções de perda mais especializadas, mas os princípios fundamentais provavelmente persistirão. Para se aprofundar no aprendizado de máquina e seus aplicativos, explore o curso Machine Learning Scientist with Python do DataCamp.