Die Pareto-Verteilung verstehen: Ein umfassender Leitfaden

Hast du schon mal eine Pizza-Party veranstaltet und dabei etwas Interessantes festgestellt? Ja, das habe ich. Bei meinem letzten Treffen habe ich beobachtet, dass die meisten Leute nur ein oder zwei Stücke gegessen haben, aber eine Handvoll Gäste hat fast die Hälfte der Pizzen verschlungen. Als ich diese Entwicklung beobachtete, wurde mir klar, dass es sich hier um einen Fall handelt: Ich war Zeuge eines realen Beispiels für eines der faszinierendsten Muster in der Datenwissenschaft - die Pareto-Verteilung.

Ich liebe dieses Beispiel, weil es perfekt wiedergibt, worum es bei der Pareto-Verteilung geht: die Beobachtung, dass in vielen Situationen eine kleine Gruppe für einen großen Teil des Ergebnisses verantwortlich ist.

Als Datenwissenschaftler weiß ich zu schätzen, wie diese Verteilung uns hilft, Situationen zu verstehen und zu modellieren, in denen die "wenigen Wichtigen" die "vielen Unwichtigen" dominieren. Überlege es dir: 20 % der Kunden eines Unternehmens erwirtschaften oft 80 % des Umsatzes, oder 20 % der Inhalte einer Website sorgen für 80 % der Besucher. Dieses Muster ist so verbreitet, dass es als Pareto-Prinzip oder als "80/20-Regel" bekannt geworden ist, obwohl die genauen Verhältnisse variieren können.

Das Besondere an der Pareto-Verteilung ist, dass sie nicht nur eine zufällige Beobachtung ist, sondern ein leistungsstarkes mathematisches Werkzeug, mit dem wir diese unausgewogenen Muster in Daten modellieren und vorhersagen können. Ganz gleich, ob du wirtschaftliche Ungleichheit analysierst, Geschäftsabläufe optimierst oder Naturphänomene untersuchst, das Verständnis der Pareto-Verteilung kann wertvolle Erkenntnisse darüber liefern, warum die Dinge nicht immer gleichmäßig verteilt sind - und was das für unsere Analyse bedeutet.

Die einzigartige Fähigkeit der Pareto-Verteilung, Ungleichgewichte aufzuzeigen, hat sie in Bereichen von der Wirtschaft bis zu den Naturwissenschaften unentbehrlich gemacht. Wenn du ähnliche statistische Muster erforschen willst, solltest du dir die Grundlagen der Wahrscheinlichkeitsrechnung in Python oder Multivariate Wahrscheinlichkeitsverteilungen in R ansehen, um dein analytisches Instrumentarium zu erweitern. Für visuelle Lernende ist der Spickzettel "Einführung in die Wahrscheinlichkeitsrechnung " ein hervorragendes Nachschlagewerk für die wichtigsten Prinzipien.

Was ist die Pareto-Verteilung?

Als der italienische Ökonom Vilfredo Pareto 1896 in seinen Garten blickte, bemerkte er etwas Seltsames: 20% seiner Erbsenschoten enthielten 80% der Erbsen. Diese Beobachtung veranlasste ihn, ähnliche Muster im Landbesitz zu erforschen. Dabei stellte er fest, dass 80 % des italienischen Bodens 20 % der Bevölkerung gehörten. Was als Gartenbeobachtung begann, entwickelte sich zu einem der vielseitigsten Werkzeuge der Statistik, um ungleichmäßige Verteilungen zu verstehen.

Historischer Hintergrund

Ende des 19. Jahrhunderts gingen die Forschungen von Vilfredo Pareto weit über Erbsenschoten und Landbesitz hinaus. Er analysierte die Verteilung des Reichtums in verschiedenen Ländern und Zeiträumen und entdeckte dabei eine konsistente mathematische Beziehung. In jeder Gesellschaft, die er untersuchte, besaß die wohlhabende Minderheit die Mehrheit des Vermögens. Dieses Muster trat so konsequent auf, dass andere Forscher begannen, seine Ideen auf verschiedene Bereiche anzuwenden, von der Wirtschaft bis zu den Naturwissenschaften.

Die Verteilung wurde bekannt, als der Unternehmensberater Joseph Juran 1937 auf Paretos Arbeit stieß. Juran nannte das Muster das "Pareto-Prinzip" und wandte es auf die Qualitätskontrolle an, indem er zeigte, dass die meisten Produktionsfehler auf eine kleine Anzahl von Ursachen zurückzuführen sind. Diese Anwendung trug dazu bei, das industrielle Qualitätsmanagement zu verändern und weckte ein breiteres Interesse an Paretos Ideen.

Wesentliche Merkmale 

Die Pareto-Verteilung unterscheidet sich von anderen statistischen Verteilungen durch mehrere einzigartige Eigenschaften:

1. Potenzgesetz-Verhalten: Im Gegensatz zur Glockenkurve (Normalverteilung), bei der die Extremwerte exponentiell selten werden, folgt die Pareto-Verteilung einem Potenzgesetz. Das bedeutet, dass Extremwerte häufiger auftreten, als du vielleicht erwartest.
2. Skaleninvarianz: Wenn du einen Teil einer Pareto-Verteilung heranzoomst, sieht das Muster ähnlich aus wie das Ganze. Diese Eigenschaft, die als Skaleninvarianz bekannt ist, erklärt, warum die Verteilung in so unterschiedlichen Kontexten auftritt.
3. Das 80/20-Prinzip: Auch wenn die genauen Zahlen variieren können (z.B. 90/10 oder 70/30), bleibt der Kerngedanke bestehen: Ein kleiner Prozentsatz der Ursachen erzeugt einen großen Prozentsatz der Wirkungen.
4. Schwerer Schwanz: Der "Schwanz" der Verteilung (der Teil, der größere Werte darstellt) nimmt langsamer ab als bei Exponentialverteilungen. Diese mathematische Eigenschaft erklärt, warum Extremwerte - wie Milliardäre in der Vermögensverteilung - häufiger vorkommen, als es eine Normalverteilung vorhersagen würde.

Aufgrund dieser Eigenschaften eignet sich die Pareto-Verteilung besonders gut zur Modellierung von Situationen, in denen sich Ressourcen, Wirkungen oder Ergebnisse auf eine kleine Teilmenge einer Bevölkerung konzentrieren.

Mathematische Formulierung der Pareto-Verteilung

Lass uns die Mathematik hinter der Pareto-Verteilung in verdauliche Stücke zerlegen. Auch wenn die Formeln auf den ersten Blick einschüchternd wirken, werde ich dich Schritt für Schritt durch die einzelnen Komponenten führen.

Pareto-Verteilungsformel

Die Wahrscheinlichkeitsdichtefunktion (PDF) der Pareto-Verteilung hat diese Form:

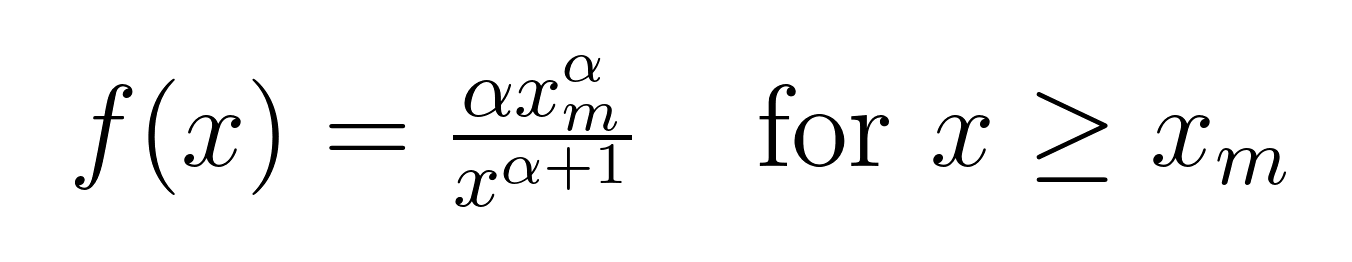
Lass uns entschlüsseln, was jedes Symbol bedeutet:

• x ist unsere Zufallsvariable (wie Reichtum, Stadtgröße oder Website-Verkehr)
• xₘ ist der kleinstmögliche Wert von x (auch Skalenparameter genannt)
• α (Alpha) ist der Formparameter, der bestimmt, wie schnell das Heck abfällt

Die kumulative Verteilungsfunktion (CDF) gibt uns die Wahrscheinlichkeit, dass ein Wert kleiner oder gleich x ist:

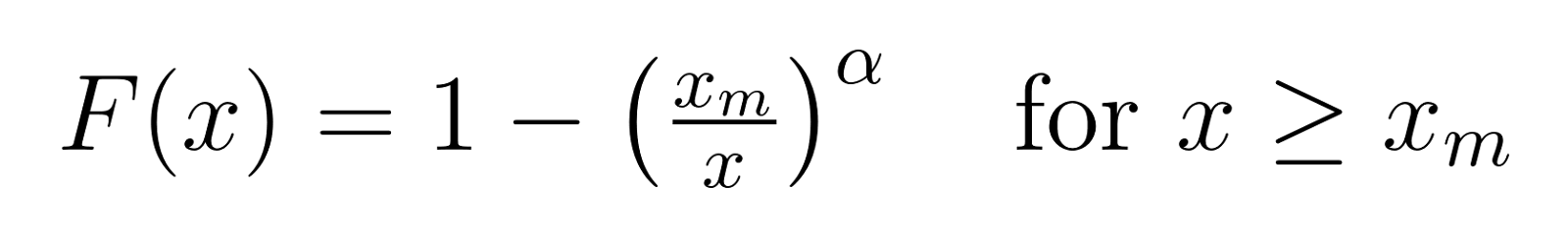
Um diese Formeln konkreter zu machen, schauen wir uns an, was verschiedene Werte von α bedeuten:

Das Pareto-Prinzip verstehen

Die berühmte 80/20-Regel ergibt sich natürlich aus der Pareto-Verteilung, wenn α ≈ 1,16.

Bei der Datenanalyse hilft uns dieses Prinzip:

1. Identifizierung von Faktoren mit hohem Einfluss in unserem Datensatz
2. Ressourcen auf die einflussreichsten Variablen konzentrieren
3. Vorhersagen, wo Extremwerte auftreten könnten
4. Setze realistische Erwartungen an die Datenverteilung

Bei der Analyse von Kundendaten könnten wir zum Beispiel feststellen, dass:

• 20% der Produkte generieren 80% des Umsatzes
• 20% der Fehlerbehebungen lösen 80% der Kundenbeschwerden
• 20% der Marketingkampagnen führen zu 80% der Neuanmeldungen

Diese Erkenntnisse helfen Unternehmen, fundierte Entscheidungen darüber zu treffen, worauf sie ihre Bemühungen konzentrieren sollten, um eine maximale Wirkung zu erzielen.

Anwendungen der Pareto-Verteilung

Von der Wirtschaftspolitik bis hin zu Naturkatastrophen - die Pareto-Verteilung taucht an überraschenden Orten auf.

Wirtschaft und Wohlstandsverteilung

Wenn du das Finanzviertel eines Landes betrittst, siehst du die Pareto-Verteilung in Aktion. Banken und Wirtschaftswissenschaftler nutzen ihn, um die Vermögenskonzentration zu verfolgen, Einkommensunterschiede zu modellieren und die Steuerpolitik zu analysieren. Als Ökonomen zum Beispiel den weltweiten Reichtum im Jahr 2023 untersuchten, stellten sie fest, dass die reichsten 1% der Erwachsenen 44% des weltweiten Reichtums besitzen. Diese Verteilung hilft politischen Entscheidungsträgern, das Wohlstandsgefälle zu verstehen und wirtschaftliche Interventionen zu entwerfen. Wenn du dich für Ideen zur Vermögensverteilung interessierst, haben wir Tutorials zum Gini-Koeffizienten und zur Lorenzkurve.

Geschäft und Marketing

In der Wirtschaft hilft das Pareto-Prinzip Unternehmen, intelligenter zu arbeiten, nicht härter. Nehmen wir an, eine E-Commerce-Website analysiert ihre Kundendaten:

• Kundensegmentierung: Identifiziere und behalte die VIP-Kunden, die den meisten Umsatz generieren
• Inventarverwaltung: Konzentriere dich auf die Produkte mit dem höchsten Umsatz und optimiere die Lagerung
• Ressourcenzuweisung: Vertriebsteams auf vielversprechende Leads ausrichten und Kernfunktionen priorisieren

Naturphänomene und wissenschaftliche Forschung

Auch die Natur folgt dem Pareto-Muster. Wissenschaftlerinnen und Wissenschaftler nutzen diese Verteilung, um sie zu untersuchen:

• Geografische Muster: Stadtbevölkerung, Flussnetzwerke, Größe der Waldbrände
• Geologische Ereignisse: Erdbebenstärken und Nachbeben
• Biologische Systeme: Artenreichtum in Ökosystemen

Nehmen wir Erdbeben - ihre Stärkeverteilung folgt einem Pareto-Muster, mit vielen kleinen Erschütterungen und seltenen verheerenden Beben. Dieses Verständnis hilft Seismologen, bessere Vorhersagemodelle und Risikobewertungen zu entwickeln.

Visualisierung der Pareto-Verteilung

Die Datenvisualisierung bringt die einzigartigen Eigenschaften der Pareto-Verteilung zum Leben. Sehen wir uns an, wie diese Verteilung grafisch aussieht und was ihre Form über die Daten aussagt, die wir analysieren.

Grafische Darstellung

Die gängigste Art, die Pareto-Verteilung zu visualisieren, ist ihre Wahrscheinlichkeitsdichtefunktion (PDF). Das zeigt uns, wie die Werte über unseren Datensatz verteilt sind.

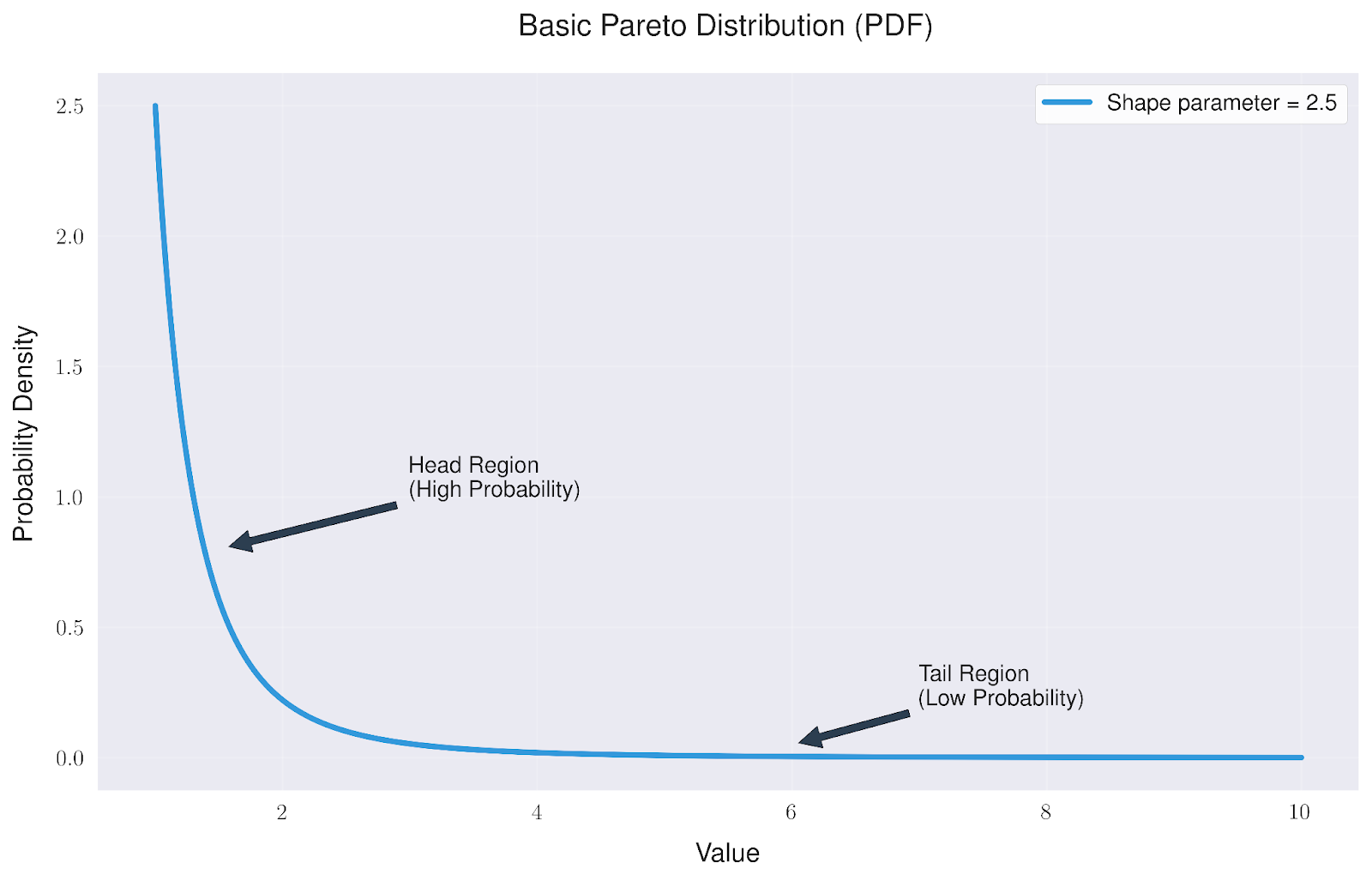
Die grundlegende Pareto-Verteilung hat eine charakteristische Form, die uns zwei wichtige Dinge verrät:

1. Die "Kopf"-Region zeigt eine hohe Konzentration von Wahrscheinlichkeiten in der Nähe des Mindestwertes
2. Der "Schwanz"-Bereich reicht weit nach rechts und zeigt, dass Extremwerte zwar selten sind, aber häufiger vorkommen als in vielen anderen Verteilungen

Was die Pareto-Verteilung besonders interessant macht, ist, wie sie sich mit verschiedenen Formparametern verändert. Diese Parameter beeinflussen direkt, wie extrem unsere Werte sein können.

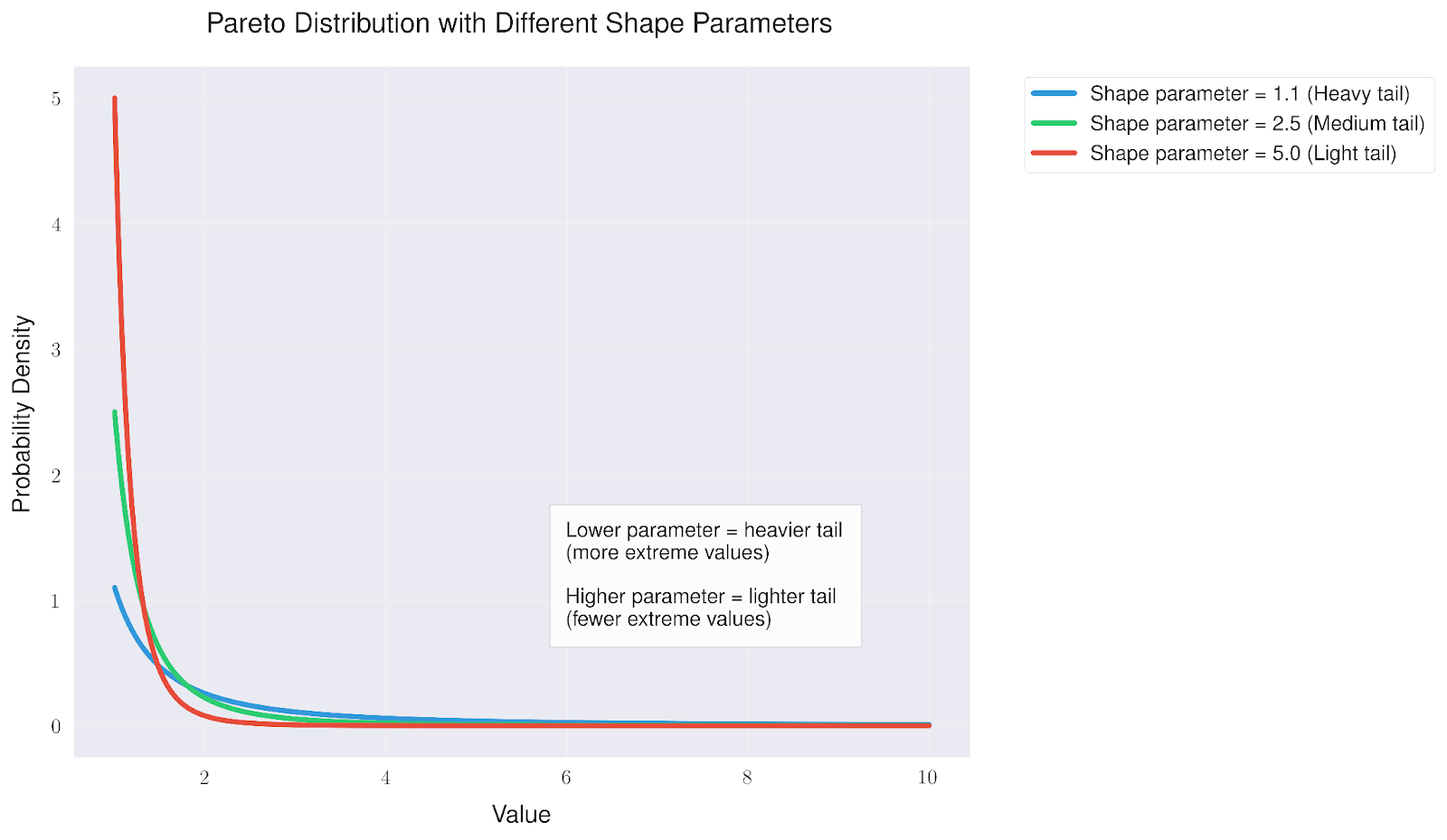
Ein Blick auf die verschiedenen Formparameter zeigt, dass:

• Niedrigere Werte (wie 1,1) erzeugen einen "dicken Schwanz", in dem extreme Werte wahrscheinlicher sind.
• Mittlere Werte (um 2,5) bieten ein Gleichgewicht zwischen häufigen und extremen Ereignissen
• Höhere Werte (wie 5,0) erzeugen einen "leichten Schweif", in dem extreme Werte immer seltener werden

Dank dieser Flexibilität eignet sich die Pareto-Verteilung für die Modellierung verschiedener Phänomene in der realen Welt, von der Verteilung des Reichtums (oft mit starkem Schwanz) bis hin zu Produktionsfehlern (meist mit leichterem Schwanz).

Die Vermögensverteilung ist oft stark schwanzlastig, was eine nicht zu vernachlässigende Wahrscheinlichkeit für extrem hohe Werte bedeutet, sodass seltene, aber massive Ereignisse (wie Milliardäre) große Auswirkungen haben. Das macht Sinn, denn es gibt einen Zinseszinseffekt, weil Menschen mit Geld investieren können. Verteilungen mit leichtem Schwanz (wie einige Arten von Produktionsfehlern) zerfallen aufgrund begrenzter, stabiler Prozesse schneller, d. h. Extremwerte sind viel unwahrscheinlicher, da große Abweichungen selten sind.

Tools für die Visualisierung

Um die Pareto-Verteilung zu visualisieren, setzen wir vor allem auf statistische Programmiersprachen und spezielle Software. Python ist eine beliebte Wahl, denn es bietet leistungsstarke Bibliotheken wie scipy.stats für Berechnungen sowie matplotlib und seaborn für die Erstellung klarer, veröffentlichungsreifer Visualisierungen. Mit seinen robusten eingebauten statistischen Funktionen und dem vielseitigen ggplot2-Paket für die grafische Darstellung ist R auch in diesem Bereich hervorragend. 

Excel eignet sich zwar hervorragend für die Erstellung von Pareto-Diagrammen (Balkendiagramme, die das 80/20-Prinzip zeigen), aber es ist nicht das beste Werkzeug, um die Pareto-Wahrscheinlichkeitsverteilung selbst zu visualisieren und damit zu arbeiten. Für die richtige statistische Analyse und Visualisierung der Pareto-Verteilung empfehlen wir dir, die oben genannten Programmiertools zu verwenden.

Um dein Verständnis für die Visualisierung von Wahrscheinlichkeitsverteilungen zu vertiefen, können dir mehrere Ressourcen als wertvolle Ausgangspunkte dienen. Das Tutorial über Wahrscheinlichkeitsverteilungen in Python bietet praktische Erfahrungen mit der Implementierung verschiedener Verteilungen, einschließlich detaillierter Beispiele unter Verwendung der statistischen Bibliotheken von Python. Für diejenigen, die sich für die visuellen Aspekte interessieren, behandelt der Artikel Datenvisualisierungen, die Verteilungen erfassen Techniken, die speziell dafür entwickelt wurden, statistische Verteilungen effektiv darzustellen. Der Spickzettel zur Datenvisualisierung schließlich dient als Schnellreferenz für die Auswahl und Erstellung geeigneter Visualisierungen für verschiedene Arten von Verteilungsdaten. Diese Ressourcen bieten eine gute Grundlage für das Verständnis und die Visualisierung der Pareto-Verteilung.

Beschränkungen und Herausforderungen der Pareto-Verteilung

Jedes statistische Instrument hat seine Grenzen, und die Pareto-Verteilung ist da keine Ausnahme. Es ist zwar ein mächtiges Objektiv für die Betrachtung bestimmter Datentypen, aber es ist genauso wichtig zu wissen, wann es nicht eingesetzt werden sollte, wie zu wissen, wann es perfekt passt. Ich möchte dir einige wichtige Punkte nennen, auf die du bei der Arbeit mit dieser Verteilung achten solltest.

Annahmen und Beschränkungen

Stell dir die Pareto-Verteilung wie ein spezielles Kameraobjektiv vor - es funktioniert hervorragend für bestimmte Aufnahmen, kann aber andere verzerren. Ihre Grundannahmen sind die technischen Spezifikationen, die wir beachten müssen:

Erstens gibt es die Anforderung des Mindestwerts. Im Gegensatz zu einigen anderen Verteilungen, die mit jeder beliebigen Zahl umgehen können, braucht die Pareto-Verteilung einen eindeutigen Startpunkt über Null. Das ist wie ein Mindesteinsatz in einem Casino - du kannst nicht mit weniger als diesem Betrag spielen. Das wird besonders knifflig, wenn deine Daten Nullen oder negative Werte enthalten, z. B. bei der Verfolgung von Gewinn- und Verlustszenarien.

Die Verteilung geht auch davon aus, dass jedes Ereignis für sich steht, unabhängig von den anderen. Aber das echte Leben funktioniert selten so. Zum Beispiel die Anhäufung von Reichtum: Wenn du Geld hast, ist es oft einfacher, mehr Geld zu verdienen. Diese Zusammenhänge können dazu führen, dass die Pareto-Verteilung weniger genau ist, als wir hoffen.

Am interessantesten ist vielleicht, dass die Verteilung von einer Skaleninvarianz ausgeht - der Idee, dass relative Unterschiede wichtiger sind als absolute. Das trifft zwar oft zu, aber in der Realität wird diese Regel manchmal gebrochen. Die Verdopplung des Vermögens einer Person wirkt sich zum Beispiel bei verschiedenen Vermögensstufen sehr unterschiedlich aus.

Fehlinterpretationen und häufige Fallstricke

Meiner Erfahrung nach gibt es mehrere Fallen, in die selbst erfahrene Analysten bei der Arbeit mit der Pareto-Verteilung tappen können. 

Die häufigste ist die Übergeneralisierung. Nur weil du ein 80/20-ähnliches Muster siehst, bedeutet das nicht automatisch, dass es sich um eine Pareto-Verteilung handelt. Das ist so, als würdest du jeden Vogel, den du siehst, für einen Adler halten - die Form mag ähnlich sein, aber auf die Details kommt es an. Teste immer, ob deine Verteilung passt, bevor du Schlussfolgerungen ziehst.

Eine weitere Herausforderung stellt die Parameterschätzung dar. Der Formparameter (α) kann besonders empfindlich auf Ausreißer reagieren, vor allem bei kleineren Datensätzen. Es ist, als würde man versuchen, die Durchschnittsgröße einer Population zu messen - ein paar sehr große oder kleine Personen können deine Ergebnisse erheblich verfälschen, wenn deine Stichprobe zu klein ist.

Wenn es um die Vorhersage von Extremereignissen geht, kann der schwere Schwanz der Pareto-Verteilung sowohl ein Segen als auch ein Fluch sein. Sie ist zwar gut geeignet, um die Möglichkeit extremer Ergebnisse zu modellieren, aber manchmal suggeriert sie auch, dass diese wahrscheinlicher sind, als sie tatsächlich sind. Das ist besonders wichtig bei Szenarien zur Risikobewertung - du willst seltene Ereignisse weder über- noch unterschätzen.

Schließlich gibt es noch das, was ich "Kontextblindheit" nenne - wir sind so sehr von der mathematischen Eleganz der Verteilung gefangen, dass wir vergessen zu fragen, ob sie für unsere spezielle Situation sinnvoll ist. Denk daran, dass die Karte nicht das Gebiet ist und die Pareto-Verteilung nur eine Karte unter vielen ist.

Ziehe im Zweifelsfall alternative Verteilungen in Betracht und überprüfe deine Annahmen immer anhand des realen Wissens über deinen Bereich. Schließlich sollte die Statistik unserem Verständnis der Realität dienen und nicht umgekehrt.

Das Pareto-Prinzip im echten Leben

Der Bauplan der Natur in der Ökosystemdynamik

In natürlichen Ökosystemen zeigt sich das Pareto-Prinzip durch das faszinierende Konzept der Schlüsselarten - jener wenigen Organismen, die einen überragenden Einfluss auf ihre Umwelt ausüben. Denk daran, wie Wölfe im Yellowstone alles von Elchpopulationen bis hin zu Flussmustern beeinflussen, oder wie Korallenriffe, die nur einen winzigen Teil des Ozeans ausmachen, fast ein Viertel aller Meeresarten beherbergen. Diese natürliche 80/20-Verteilung zeigt sich in allem, von der Größe der Baumkronen bis zur Verteilung der Niederschläge über die Jahreszeiten.

Die Sinfonie der Wohlstandsverteilung

Stell dir die Verteilung des Reichtums wie eine Orchesteraufführung vor, bei der einige Schlüsselinstrumente die Hauptmelodie tragen, während andere den wichtigen Hintergrund liefern. So wie die erste Geige oft das Orchester anführt, besitzt ein kleiner Prozentsatz von Einzelpersonen die Mehrheit des weltweiten Reichtums und schafft so eine komplexe wirtschaftliche Zusammensetzung. Dieses Muster hat tiefgreifende Auswirkungen auf die Wirtschaftspolitik und wirft die Frage auf, wie die Dynamik, die durch die Vermögenskonzentration entstehen kann, und die soziale Harmonie, die eine breitere Beteiligung erfordert, erhalten werden können. Das Verständnis dieser musikalischen Parallele hilft uns, sowohl die Effizienz als auch die Herausforderungen der Vermögenskonzentration zu verstehen.

Die Innovationsregel: Wenn weniger mehr schafft

Im Bereich der Innovation zeigt sich das Pareto-Prinzip darin, dass bahnbrechende Ideen nur aus einer überraschend kleinen Anzahl von Versuchen hervorgehen. Unternehmen wie Apple und Google haben herausgefunden, dass etwa 20 % ihrer Produkte 80 % ihres Umsatzes generieren, während in der wissenschaftlichen Forschung ein kleiner Teil der Arbeiten die meisten Zitate erhält. Dieses Muster zeigt sich in allen kreativen Branchen, von den Hits in den Musikkatalogen bis zu den Blockbuster-Filmen in den Studio-Portfolios.

Soziale Wellen: der Netzwerkeffekt

Das Pareto-Prinzip wirkt sich darauf aus, wie sich Informationen in sozialen Netzwerken verbreiten. Einige wenige Influencer, die vielleicht 20% der Nutzer repräsentieren, sorgen oft für 80% des Engagements auf sozialen Plattformen. Das gleiche Muster zeigt sich bei der Viralität von Inhalten, bei denen ein kleiner Prozentsatz der Beiträge die Mehrheit der Likes und Interaktionen auf sich vereint.

Fazit

Die Pareto-Verteilung zeigt, wie statistische Werkzeuge aussagekräftige Konzentrationsmuster in Daten aufdecken können. Um dein Verständnis für solche Konzepte zu erweitern, bieten wir dir wertvolle Lernmöglichkeiten. Unser Kurs Grundlagen der Wahrscheinlichkeitsrechnung in R führt in die Grundprinzipien ein, während der Kurs Einführung in die Portfolioanalyse in R zeigt, wie diese Ideen auf finanzielle Zusammenhänge angewendet werden. Außerdem bietet unser Poker Probabilistik & Statistik mit Python-Tutorial eine einzigartige Möglichkeit, Wahrscheinlichkeitskonzepte in der Praxis zu erforschen, was das Lernen sowohl spannend als auch praktisch macht. Diese Ressourcen bieten eine solide Grundlage, um statistische Erkenntnisse in einer Reihe von praktischen Szenarien anzuwenden.