Fonction de perte d'entropie croisée dans l'apprentissage automatique : Améliorer la précision des modèles

Comprendre l'entropie

Le concept d'entropie croisée trouve ses racines dans le domaine de la théorie de l'information, où l 'entropie de l'information, également connue sous le nom d'entropie de Shannon, a été formellement introduite en 1948 par Claude Shannon dans un document intitulé "A Mathematical Theory of Communication" (Théorie mathématique de la communication). Avant d'aborder la question de l'entropie croisée, abordons celle de l'entropie.

L'entropie calcule le degré de hasard ou de désordre d'un système. Dans le contexte de la théorie de l'information, l'entropie d'une variable aléatoire est l'incertitude moyenne, la surprise ou l'information inhérente aux résultats possibles. Pour simplifier, elle mesure l'incertitude d'un événement.

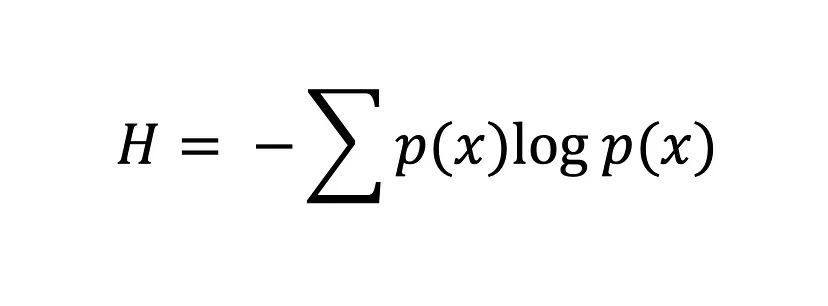
L'équation de l'entropie de Shannon

Plus la valeur de l'entropie, H(x), est élevée, plus l'incertitude de la distribution de probabilité est grande, et plus la valeur est petite, moins l'incertitude est grande.

Qu'est-ce que l'entropie croisée ?

L'entropie croisée, également connue sous le nom de perte logarithmique ou de perte logarithmique, est une fonction de perte populaire utilisée dans l'apprentissage automatique pour mesurer les performances d'un modèle de classification.

Il mesure le nombre moyen de bits nécessaires pour identifier un événement à partir d'une distribution de probabilité, p, en utilisant le code optimal pour une autre distribution de probabilité, q. En d'autres termes, l'entropie croisée mesure la différence entre la distribution de probabilité découverte d'un modèle de classification et les valeurs prédites.

La fonction de perte d'entropie croisée est utilisée pour trouver la solution optimale en ajustant les poids d'un modèle d'apprentissage automatique pendant la formation. L'objectif est de minimiser l'erreur entre les résultats réels et les résultats prévus. Une valeur d'entropie croisée plus faible indique une meilleure performance. 

Si vous connaissez la divergence de Kullback-Leibler (KL), vous vous demandez peut-être : "Quelle est la différence entre l'entropie croisée et la divergence de KL ?". C'est une bonne question. Ces deux concepts sont largement utilisés pour mesurer les différences ou les similitudes entre les distributions de probabilité. Bien qu'ils présentent certaines similitudes, ils ont des objectifs différents.

Comme indiqué ci-dessus, l'entropie croisée mesure le nombre moyen de bits nécessaires pour identifier un événement à partir d'une distribution de probabilité, P, en utilisant le code optimal pour une autre distribution de probabilité, Q. Elle est généralement utilisée dans l'apprentissage automatique pour évaluer les performances d'un modèle dont l'objectif est de minimiser l'erreur entre la distribution de probabilité prédite et la distribution réelle.

En revanche, la divergence de KL mesure la différence entre deux distributions de probabilité, P et Q. En d'autres termes, la divergence de KL quantifie la perte d'informations lorsque Q est utilisé pour approximer P. Ceci est extrêmement utile dans les tâches d'apprentissage non supervisé où l'objectif est de découvrir la structure des données en minimisant la divergence entre la vraie distribution et la distribution des données apprises.

L'entropie croisée comme fonction de perte

Dans l'apprentissage automatique, les fonctions de perte aident les modèles à déterminer à quel point ils se trompent et à s'améliorer en fonction de cette erreur. Il s'agit de fonctions mathématiques qui quantifient la différence entre les valeurs prédites et les valeurs réelles dans un modèle d'apprentissage automatique, mais ce n'est pas tout.

La mesure de l'erreur d'une fonction de perte sert également de guide pendant le processus d'optimisation en fournissant au modèle un retour d'information sur la façon dont il s'adapte aux données. C'est pourquoi la plupart des modèles d'apprentissage automatique mettent en œuvre une fonction de perte au cours de la phase d'optimisation, où les paramètres du modèle sont choisis pour aider le modèle à minimiser l'erreur et à parvenir à une solution optimale - plus l'erreur est petite, meilleur est le modèle.

Nous pouvons mesurer l'erreur entre deux distributions de probabilité à l'aide de la fonction de perte d'entropie croisée. Par exemple, supposons que nous menions une tâche de classification binaire (une tâche de classification avec deux classes, 0 et 1).

Dans ce cas, nous devons utiliser l'entropie croisée binaire, qui est l'entropie croisée moyenne de tous les échantillons de données :

Formule d'entropie croisée binaire [Source : Fonction de perte d'entropie croisée]

Si nous devions calculer la perte d'un seul point de données où la valeur correcte est y=1, voici à quoi ressemblerait notre équation :

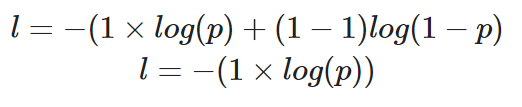
Calcul de l'entropie croisée binaire pour une seule instance où la valeur réelle est 1

La probabilité prédite, p, détermine la valeur de la perte, l. Si la valeur de p est élevée, le modèle sera récompensé pour avoir fait une prédiction correcte, ce qui sera illustré par une faible valeur de perte, l.

Cependant, une faible probabilité prédite, p, signifierait que le modèle est incorrect, et la fonction de perte d'entropie croisée binaire le reflétera en augmentant la valeur de l.

Pour une tâche de classification multi-classes, l'entropie croisée (ou l'entropie croisée catégorielle, comme on l'appelle souvent) peut être simplement étendue comme suit :

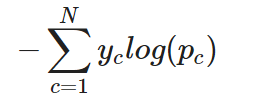
Entropie croisée catégorielle pour une seule instance

En d'autres termes, pour appliquer l'entropie croisée à une tâche de classification multi-classes, la perte pour chaque classe est calculée séparément, puis additionnée pour déterminer la perte totale.

Implémentation de la perte d'entropie croisée dans PyTorch et TensorFlow

Dans cette partie du tutoriel, nous allons apprendre à utiliser la fonction de perte d'entropie croisée dans TensorFlow et PyTorch.

Commençons par créer le jeu de données. Nous utiliserons la fonction Scikit learns make_classification pour nous aider :

from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split

 # create training data
X, y = make_classification(
    n_samples=10000,
    n_informative=10,
    random_state=2022
)

# split into train and test
X_new, X_test = X[:9000, :], X[9000:, ]
y_new, y_test = y[:9000], y[9000:]

X_train, X_val, y_train, y_val = train_test_split(
    X_new, y_new,
    test_size=0.3
)
print(f"Train data: {X_train.shape}\n\
Train labels: {y_train.shape}\n\
Test data: {X_test.shape}\n\
Test labels: {y_test.shape}")

"""
Train data: (6300, 20)
Train labels: (6300,)
Test data: (1000, 20)
Test labels: (1000,)
"""

L'entropie croisée dans TensorFlow

Le modèle que nous allons construire se compose d'une couche d'entrée, d'une couche cachée et d'une couche de sortie.

Comme il s'agit d'une tâche de classification binaire, nous utiliserons l'entropie croisée binaire comme fonction de perte.

# building and training model
model = tf.keras.Sequential([
                            tf.keras.layers.Dense(10,
                                                  input_shape=(X_train.shape[1],),
                                                  activation="relu"),
                            tf.keras.layers.Dense(10,
                                                  activation="relu"),
                            tf.keras.layers.Dense(1, activation="sigmoid")
])

model.compile(
    loss="binary_crossentropy", # loss function here
    optimizer="adam",
    metrics=["accuracy"])

history = model.fit(X_train, y_train, epochs=20, validation_data=[X_val, y_val], verbose=0)

Ensuite, nous tracerons la perte pour voir si le modèle s'améliore, c'est-à-dire que l'erreur diminue à chaque époque jusqu'à ce qu'il ne puisse plus s'améliorer.

# plotting the loss of the models
fig, ax = plt.subplots(figsize=(8,5))
plt.plot(history.history['loss'])
plt.plot(history.history['val_loss'])
plt.title('model loss')
plt.ylabel('loss')
plt.xlabel('epoch')
plt.xticks(np.arange(0,20, step=1))
plt.legend(['train', 'test'], loc='upper right')
plt.show()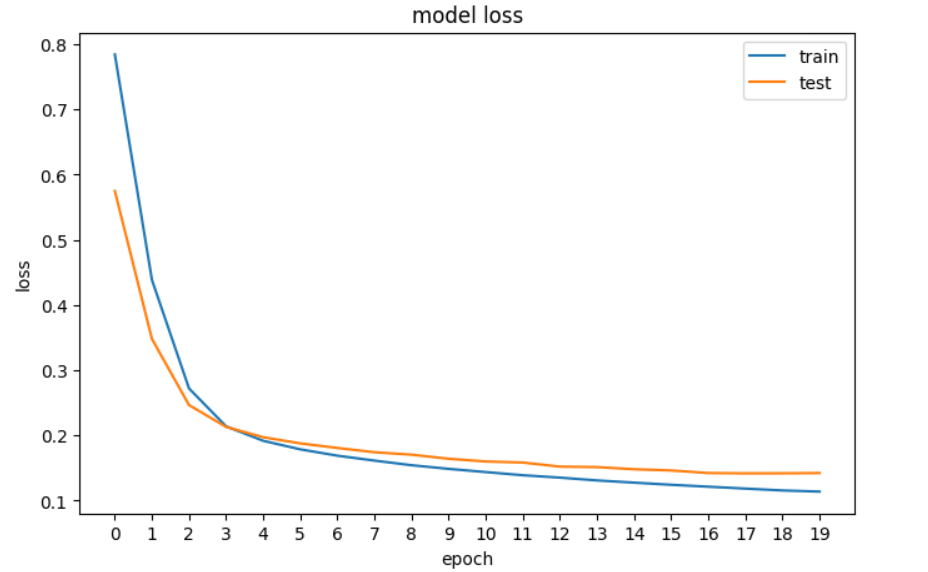

Tracé de la perte de notre réseau neuronal dans TensorFlow.

L'entropie croisée dans PyTorch

Dans PyTorch, les entrées, les sorties et les paramètres du modèle sont codés à l'aide de tenseurs, ce qui signifie que nous devons convertir nos tableaux Numpy en tenseurs. C'est la première chose que nous faisons dans le code ci-dessous, puis nous construisons le réseau neuronal et imprimons ses dimensions.

# convert numpy arrays to tensors 
X_train_tensor = torch.tensor(X_train, dtype=torch.float32)
X_val_tensor = torch.tensor(X_val, dtype=torch.float32)
y_train_tensor = torch.tensor(y_train, dtype=torch.float32).reshape(-1, 1)
y_val_tensor = torch.tensor(y_val, dtype=torch.float32).reshape(-1, 1)

# build the model
input_dim = X_train.shape[1]
hidden_dim = 10
output_dim = 1

model = nn.Sequential(
    nn.Linear(input_dim, hidden_dim),
    nn.ReLU(),
    nn.Linear(hidden_dim, hidden_dim),
    nn.ReLU(),
    nn.Linear(hidden_dim, output_dim),
    nn.Sigmoid()
    )

print(model)

"""
Sequential(
  (0): Linear(in_features=20, out_features=10, bias=True)
  (1): ReLU()
  (2): Linear(in_features=10, out_features=10, bias=True)
  (3): ReLU()
  (4): Linear(in_features=10, out_features=1, bias=True)
  (5): Sigmoid()
)
"""

Nous définissons ensuite la fonction de perte de l'entropie croisée binaire et l'optimiseur :

loss_fn = nn.BCELoss()  # binary cross entropy
optimizer = optim.Adam(model.parameters(), lr=0.001)

Et maintenant, il s'agit de tracer la perte :

# plotting the loss of the models
fig, ax = plt.subplots(figsize=(8,5))
plt.plot(train_loss)
plt.plot(val_loss)
plt.title('model loss')
plt.ylabel('loss')
plt.xlabel('epoch')
plt.xticks(np.arange(0,20, step=1))
plt.legend(['train', 'test'], loc='upper right')
plt.show()

Tracé de la perte de notre réseau neuronal dans PyTorch

Principaux enseignements

Voici un bref récapitulatif de ce que nous avons appris sur la perte d'entropie croisée :

• L'entropie calcule le degré de hasard ou de désordre au sein d'un système afin de mesurer l'incertitude d'un événement. Si un résultat est certain, la mesure de l'entropie sera faible.
• L'entropie croisée est une fonction de perte populaire utilisée dans l'apprentissage automatique pour mesurer la performance d'un modèle de classification. Elle mesure la différence entre la distribution de probabilité découverte d'un modèle de classification et les valeurs prédites. Lorsqu'elle est appliquée à des tâches de classification binaire, elle est communément appelée perte logarithmique.
• L'entropie croisée binaire est utilisée pour la classification binaire et l'entropie croisée catégorielle pour la classification multi-classes.
• L'entropie croisée est similaire à la divergence KL, mais elles ont des objectifs différents : l'entropie croisée est généralement utilisée dans l'apprentissage automatique pour évaluer les performances d'un modèle dont l'objectif est de minimiser l'erreur entre la distribution de probabilité prédite et la distribution réelle, tandis que la divergence KL est plus utile dans les tâches d'apprentissage non supervisé où l'objectif est de découvrir la structure des données en minimisant la divergence entre la distribution réelle et la distribution apprise des données.

Pour poursuivre votre apprentissage, consultez nos ressources :

• Construction de modèles de réseaux neuronaux (NN) en R
• Introduction à l'apprentissage profond en Python