UMAP verstehen: Ein umfassender Leitfaden zur Dimensionsreduktion

Bei Problemen im Bereich des maschinellen Lernens haben wir oft mit Datensätzen zu tun, die Hunderte oder sogar Tausende von Merkmalen haben, und diese Größenordnung macht es oft schwierig, die Daten sinnvoll zu visualisieren und zu analysieren. Mit den üblichen Plotting-Methoden kann man nur zwei oder drei Dimensionen gleichzeitig zeigen, was es echt schwer macht, die Struktur von hochdimensionalen Daten zu verstehen. Hier kommen Techniken zur Dimensionsreduktion wie UMAP (Uniform Manifold Approximation and Projection) ins Spiel.

Mit der Zeit hat sich UMAP zu einer beliebten Methode entwickelt, um komplexe Datensätze aus verschiedenen Bereichen zu visualisieren. Dieses Tutorial zeigt dir alles, was du über UMAP wissen musst, von den Grundlagen bis zur praktischen Umsetzung und häufigen Herausforderungen, damit du diese Technik ab jetzt in deinen Projekten nutzen kannst.

Was ist UMAP?

UMAP ist ein nichtlinearer Algorithmus zur Dimensionsreduktion, der hochdimensionale Daten in einen Raum mit geringerer Dimension (normalerweise 2D oder 3D) projiziert und dabei die grundlegende Struktur der Daten beibehält. UMAP steht für „Uniform Manifold Approximation and Projection” und basiert auf dem Manifold Learning und der topologischen Datenanalyse.

Andere Methoden zur Dimensionsreduktion, wie zum Beispiel t-SNE, sind gut darin, lokale Nachbarschaften zu erhalten, verzerren aber am Ende die globalen Beziehungen. Der Hauptvorteil von UMAP ist, dass es einen guten Mittelweg zwischen den lokalen Nachbarschaften und den globalen Beziehungen findet. Es wird angenommen, dass die Daten auf einer Riemannschen Mannigfaltigkeit liegen und dass diese Mannigfaltigkeit lokal mit einer unscharfen topologischen Struktur modelliert werden kann. Dank dieser mathematischen Grundlage kann UMAP aussagekräftigere Visualisierungen erstellen, bei denen ähnliche Datenpunkte gruppiert werden, während die Gesamttopologie des Datensatzes erhalten bleibt.

Der Algorithmus baut eine hochdimensionale Graphendarstellung der Daten auf und optimiert dann einen niedrigdimensionalen Graphen, damit er strukturell so ähnlich wie möglich ist. UMAP ist nicht nur für die Visualisierung nützlich, sondern auch als Vorverarbeitungsschritt für Clustering-Algorithmen oder sogar als allgemeine nichtlineare Technik zur Dimensionsreduktion für Machine-Learning-Pipelines.

Wie UMAP funktioniert

Wir werden den Prozess in ein paar wichtige Schritte aufteilen, um zu verstehen, wie UMAP funktioniert. Die komplette mathematische Theorie braucht fortgeschrittene Konzepte aus der Topologie und der topologischen Datenanalyse. Deshalb schauen wir uns in diesem Tutorial den Kernalgorithmus mal intuitiv an.

Schritt 1: Erstellen des hochdimensionalen Graphen

UMAP fängt damit an, einen gewichteten Graphen zu erstellen, der die Beziehungen im hochdimensionalen Raum zeigt. Für jeden Datenpunkt findet es die k nächsten Nachbarn (wobei k ein Wert ist, den wir anpassen können). Im Gegensatz zu einfachen k-NN-Graphen nutzt UMAP aber einen probabilistischen Ansatz. Es berechnet die Wahrscheinlichkeit, dass zwei Punkte miteinander verbunden sind, basierend auf ihrem Abstand, und nutzt dabei eine glatte Annäherung, die von der lokalen Dichte um jeden Punkt abhängt.

Der entscheidende Punkt hier ist, dass sich UMAP an die lokale Struktur unserer Daten anpasst. In dichten Gebieten müssen Punkte echt nah beieinander liegen, um als Nachbarn zu gelten, während der Algorithmus in dünn besiedelten Gebieten seinen Suchradius vergrößert. 

Dieses adaptive Verhalten wird durch die Formel gesteuert:

p(i,j) = exp(-(d(xi, xj) - ρi) / σi)

Dabei ist d(xi, xj) der Abstand zwischen den Punkten, ρi der Abstand zum nächsten Nachbarn und σi ein Skalierungsfaktor, der für jeden Punkt berechnet wird.

Schritt 2: Erstellen einer unscharfen topologischen Darstellung

UMAP wandelt dann diese lokalen Wahrscheinlichkeitsverteilungen in eine unscharfe topologische Struktur aus der topologischen Datenanalyse um. Es macht den Graphen symmetrisch, indem es die Wahrscheinlichkeiten aus beiden Richtungen zusammenfasst:

p(i,j) = p(i|j) + p(j|i) - p(i|j) * p(j|i)

Dadurch entsteht eine sogenannte unscharfe simpliciale Menge, die die vielfältige Struktur der hochdimensionalen Daten erfasst.

Schritt 3: Optimierung der niedrigdimensionalen Darstellung

Der letzte Schritt besteht darin, eine niedrigdimensionale Darstellung zu finden, die die unscharfe topologische Struktur beibehält. UMAP fängt damit an, Punkte im niedrigdimensionalen Raum zu setzen (mit einer spektralen Einbettung) und nutzt dann Gradientenabstieg, um die Kreuzentropie zwischen den hochdimensionalen und niedrigdimensionalen unscharfen topologischen Darstellungen zu minimieren.

Die Optimierung nutzt Anziehungskräfte, um Punkte, die nah beieinander liegen sollten (basierend auf der hochdimensionalen Struktur), zusammenzuziehen, und Abstoßungskräfte, um Punkte, die weit voneinander entfernt sein sollten, auseinanderzudrücken. Diese Push-Pull-Dynamik sorgt für die typischen Visualisierungen, bei denen Cluster gut voneinander getrennt sind und trotzdem ihre innere Struktur behalten.

Praktische Anwendungen von UMAP

UMAP kann in vielen Bereichen eingesetzt werden, wo es nützlich ist, hochdimensionale Daten zu verstehen. 

Einige dieser praktischen Anwendungen sind:

• Einzelzellgenomik und Bioinformatik: In der Genomforschung ist UMAP zum Standard für die Visualisierung von Einzelzell-RNA-Sequenzierungsdaten geworden. Forscher nutzen es, um Zelltypen zu erkennen, Entwicklungsverläufe zu verfolgen und den Verlauf von Krankheiten zu verstehen. UMAP macht verschiedene Zellgruppen und ihre Beziehungen sichtbar, die man in den Rohdaten nicht erkennen könnte, indem es Tausende von Genexpressionsmessungen in ein 2D-Diagramm packt.
• Natürliche Sprachverarbeitung: Textdaten können, wenn sie in hochdimensionale Einbettungen umgewandelt werden, mit UMAP visualisiert werden, um semantische Beziehungen zu verstehen. Es wird oft benutzt, um Wort-Embeddings und Dokument-Cluster zu zeigen und Sprachmodelle zu debuggen, indem es zeigt, wie verschiedene Konzepte im Embedding-Raum miteinander zusammenhängen.
• Computersicht und Bildanalyse: UMAP hilft dabei, die von neuronalen Netzen gelernten Merkmalsdarstellungen zu visualisieren, sodass man besser versteht, welche Muster das Modell gelernt hat. Es wird auch in Gesichtserkennungssystemen verwendet, um zu zeigen, wie Gesichter anhand ihrer Merkmale gruppiert werden, und in der medizinischen Bildgebung, um ähnliche Fälle oder Anomalien zu erkennen.
• Datenauswertung und Erkennung von Ausreißern: UMAP hilft dabei, versteckte Muster aufzudecken und Ausreißer in komplexen Datensätzen zu erkennen, indem es sie in einen verständlichen visuellen Raum projiziert. Dieser visuelle Ansatz zur Erkennung von Ausreißern ist besonders nützlich, wenn herkömmliche statistische Methoden mit hochdimensionalen Wechselwirkungen Probleme haben.
• Kundensegmentierung und Marktanalyse: Marketingteams nutzen UMAP, um das Verhalten von Kunden anhand von verschiedenen Merkmalen wie Kaufhistorie, demografischen Daten und Interaktionskennzahlen zu visualisieren. Das hilft dabei, verschiedene Kundengruppen zu erkennen und die Beziehungen zwischen den verschiedenen Gruppen zu verstehen.
• Arzneimittelforschung: Pharmazeutische Forscher nutzen UMAP, um Räume chemischer Verbindungen zu visualisieren. So können sie vielversprechende Wirkstoffkandidaten identifizieren, indem sie sehen, welche Verbindungen sich in der Nähe bekannter wirksamer Medikamente gruppieren und gleichzeitig weit entfernt von toxischen Verbindungen sind.

Nachdem wir jetzt das Konzept, die mathematischen Grundlagen und die praktischen Anwendungen von UMAP verstanden haben, lass uns zur Umsetzung übergehen.

Implementierung von UMAP in Python

Probieren wir UMAP mal mit einem echten Datensatz aus, um zu sehen, wie es in der Praxis funktioniert. Wir nehmen den Olivetti Faces-Datensatz, der Graustufenbilder von Gesichtern von 40 verschiedenen Leuten enthält. Der Olivetti-Datensatz kann von Kaggle oder über die Python-Bibliothek scikit-learn runtergeladen werden.

Der Olivetti Faces-Datensatz hat:

• 400 Graustufenbilder (64 x 64 Pixel = 4096 Dimensionen)
• 40 verschiedene Leute
• 10 Bilder pro Person (unterschiedliche Gesichtsausdrücke, Lichtverhältnisse)

Das ist super für UMAP, weil wir erwarten, dass Bilder derselben Person zusammen gruppiert werden, auch wenn es Unterschiede in Ausdruck und Beleuchtung gibt.

Schritt 1: Bibliotheken importieren und die Daten laden

Zuerst importieren wir die benötigten Bibliotheken und laden unseren Datensatz:

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import matplotlib.cm as cm
from sklearn.datasets import fetch_olivetti_faces
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
import umap
import warnings
warnings.filterwarnings('ignore')

# Load the Olivetti faces dataset
faces = fetch_olivetti_faces(shuffle=True, random_state=42)
X = faces.data
y = faces.target

print(f"Dataset shape: {X.shape}")
print(f"Number of individuals: {len(np.unique(y))}")
print(f"Number of images per individual: {X.shape[0] // len(np.unique(y))}")

# Display sample faces
fig, axes = plt.subplots(2, 5, figsize=(12, 6))
for i, ax in enumerate(axes.flat):
   ax.imshow(X[i].reshape(64, 64), cmap='gray')
   ax.set_title(f'Person {y[i]}')
   ax.axis('off')
plt.suptitle('Sample Faces from the Dataset')
plt.tight_layout()
plt.show()

Aus dem obigen Code können wir den Datensatz wie folgt visualisieren:

Schritt 2: Wende UMAP mit den Standardparametern an.

Der Olivetti-Gesichtsdatensatz ist schon mit Pixelwerten zwischen 0 und 1 normalisiert, also können wir UMAP direkt drauf anwenden:

# Create UMAP instance with default parameters
reducer = umap.UMAP(random_state=42)

# Fit and transform the data
embedding = reducer.fit_transform(X)

# Create a custom colormap for 40 distinct classes
colors = cm.get_cmap('hsv', 40)  

# Create visualization
plt.figure(figsize=(12, 10))
scatter = plt.scatter(embedding[:, 0], embedding[:, 1], c=y,
                    cmap=colors, s=50, alpha=0.8, edgecolors='black', linewidth=0.5)
plt.colorbar(scatter, label='Person ID', ticks=np.arange(0, 40, 5))
plt.title('UMAP Projection of Olivetti Faces (Default Parameters)')
plt.xlabel('UMAP 1')
plt.ylabel('UMAP 2')
plt.grid(True, alpha=0.3)
plt.show()

Wir sehen ein farbiges Streudiagramm als UMAP-Visualisierung:

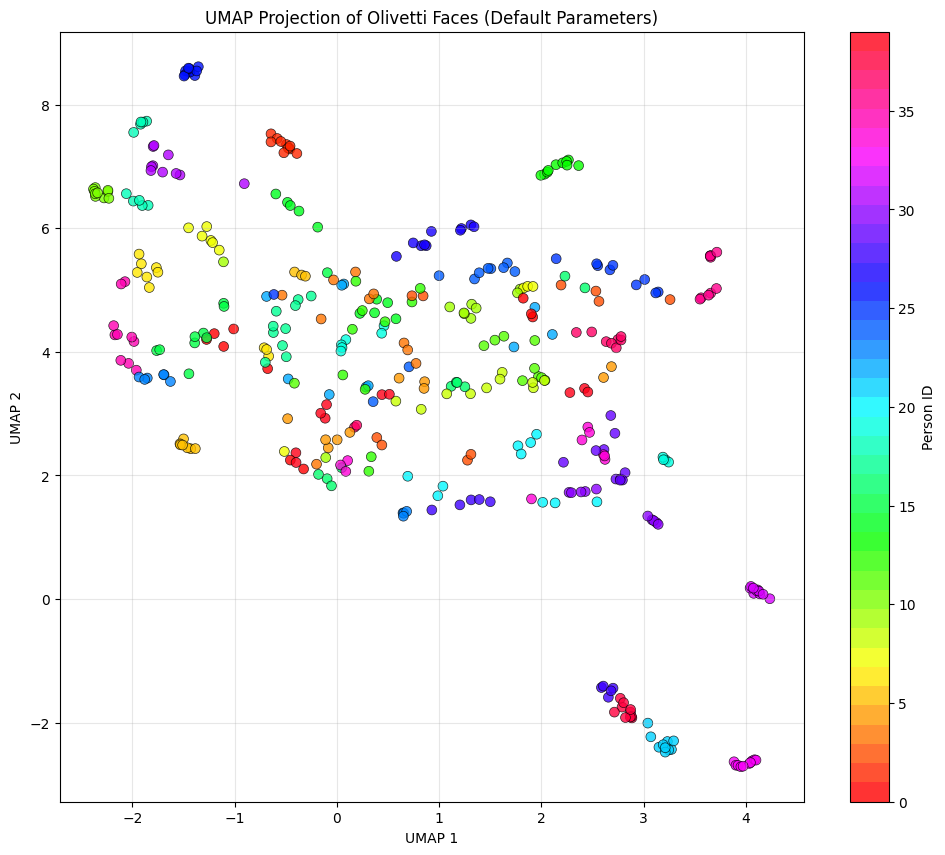
Hier sind ein paar Sachen, die du beachten solltest, um das Diagramm besser zu verstehen:

• Jeder Punkt steht für ein Gesicht.
• Die Farben stehen für verschiedene Leute (Personen-ID 0–39).
• Nähe bedeutet Ähnlichkeit: Nah beieinander liegende Punkte sind Flächen, die UMAP im 4096-dimensionalen Raum als ähnlich ansieht.

Auch wenn das in der Praxis nicht so läuft, würden wir uns wünschen, dass alle 10 Bilder derselben Person (derselben Farbe) zusammen gruppiert werden. Auf dem Bild sehen wir, dass einige ähnliche Farben zusammen gruppiert sind, als wir das UMAP mit den Standardparametern erstellt haben.

Schritt 3: Entdecke die wichtigsten UMAP-Parameter

UMAP hat ein paar wichtige Parameter, die sein Verhalten steuern. Schauen wir mal, wie sie die Ergebnisse beeinflussen:

# Create subplots for different parameter settings
fig, axes = plt.subplots(2, 3, figsize=(18, 12))
axes = axes.ravel()

# Different parameter configurations
param_configs = [
   {'n_neighbors': 5, 'min_dist': 0.1},
   {'n_neighbors': 15, 'min_dist': 0.1},
   {'n_neighbors': 50, 'min_dist': 0.1},
   {'n_neighbors': 15, 'min_dist': 0.0},
   {'n_neighbors': 15, 'min_dist': 0.5},
   {'n_neighbors': 15, 'min_dist': 0.99}
]

# Apply UMAP with different parameters
for idx, params in enumerate(param_configs):
   reducer = umap.UMAP(random_state=42, **params)
   embedding = reducer.fit_transform(X_scaled)
  
   ax = axes[idx]
   scatter = ax.scatter(embedding[:, 0], embedding[:, 1], c=y,
                       cmap='tab20', s=30, alpha=0.8)
   ax.set_title(f"n_neighbors={params['n_neighbors']}, "
                f"min_dist={params['min_dist']}")
   ax.set_xlabel('UMAP 1')
   ax.set_ylabel('UMAP 2')
   ax.grid(True, alpha=0.3)

plt.tight_layout()
plt.show()

Die Visualisierung der Ausgabe sieht so aus:

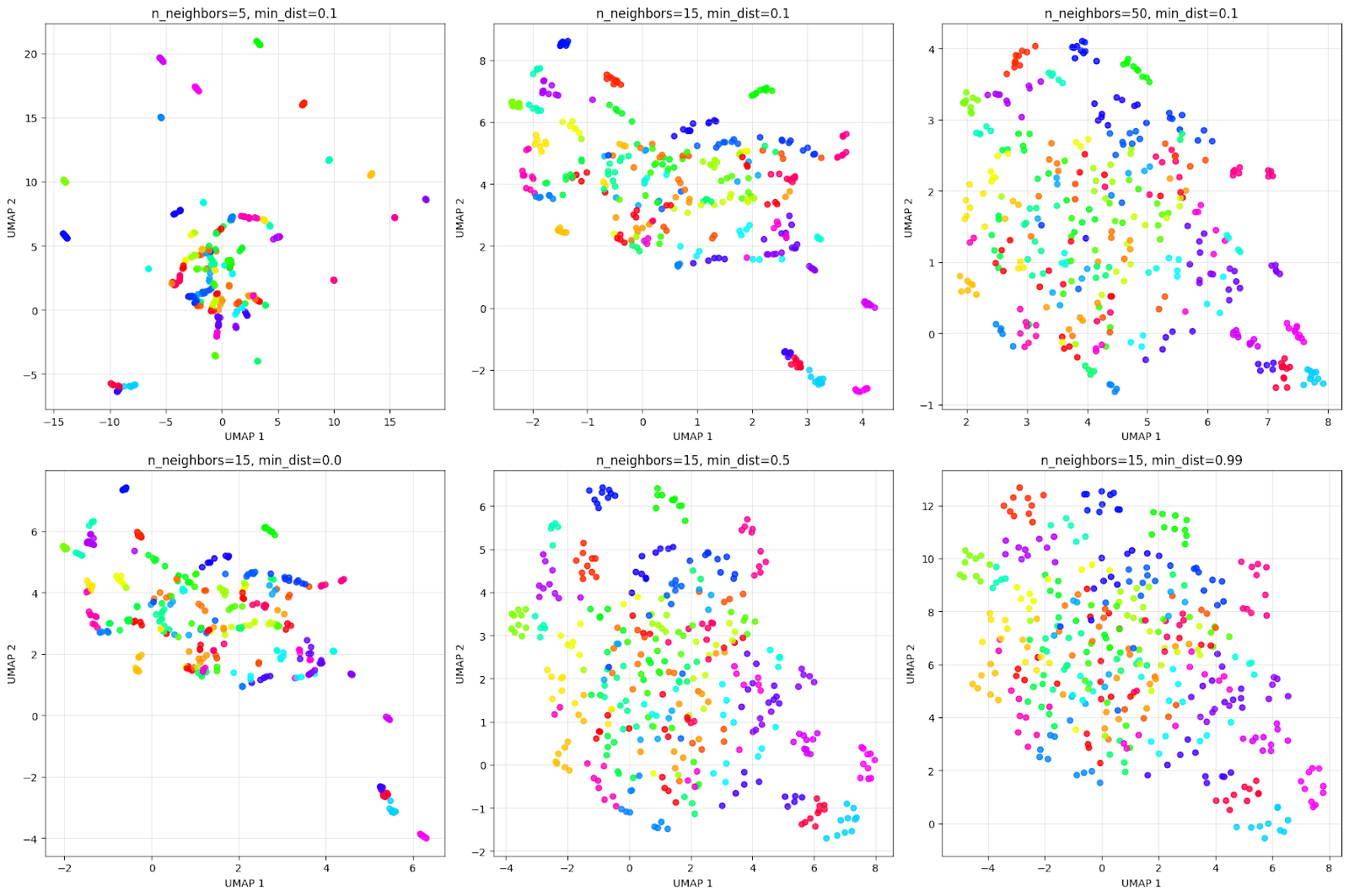
Das obige Raster zeigt, wie Parameter die Visualisierung beeinflussen. Wenn man die obere Zeile des n_neighbors-Effekts betrachtet:

• n_neighbors=5: Sehr lokale Sichtweise, erzeugt viele kleine, enge Cluster.
• n_neighbors=15: Ausgewogene Sichtweise, bietet eine gute Mischung aus lokaler und globaler Struktur.
• n_neighbors=50: Global gesehen konzentriert es sich auf die Gesamtstruktur und führt möglicherweise ähnliche Personen zusammen.

Schau dir mal die untere Zeile des min_dist-Effekts an:

• min_dist=0.0: Die Punkte liegen echt nah beieinander, wie man in der Tabelle sehen kann. Dadurch entstehen echt kompakte, dichte Cluster.
• min_dist=0.5: Mittlerer Abstand, der zu weiter auseinander liegenden Clustern führt.
• min_dist=0.99: Der maximale Abstand sorgt dafür, dass die Punkte gleichmäßig verteilt sind, aber die Clusterstruktur geht dabei verloren.

Es ist immer gut, mit diesen Einstellungen rumzuprobieren, um das beste Clustering-Ergebnis für das jeweilige Problem zu kriegen.

Alternativen zu UMAP für die Dimensionsreduktion

Lass uns unser Beispiel mit dem Olivetti-Datensatz weitermachen, um UMAP mit PCA und t-SNE zu vergleichen und ihre Unterschiede zu verstehen:

from sklearn.decomposition import PCA
from sklearn.manifold import TSNE

# Create figure with subplots
fig, axes = plt.subplots(1, 3, figsize=(18, 6))

colors = cm.get_cmap('hsv', 40)

# PCA
pca = PCA(n_components=2, random_state=42)
pca_result = pca.fit_transform(X)
axes[0].scatter(pca_result[:, 0], pca_result[:, 1], c=y,
               cmap=colors, s=50, alpha=0.8)
axes[0].set_title('PCA Projection')
axes[0].set_xlabel('PC 1')
axes[0].set_ylabel('PC 2')
axes[0].grid(True, alpha=0.3)

# t-SNE
tsne = TSNE(n_components=2, random_state=42, perplexity=30)
tsne_result = tsne.fit_transform(X)
axes[1].scatter(tsne_result[:, 0], tsne_result[:, 1], c=y,
               cmap=colors, s=50, alpha=0.8)
axes[1].set_title('t-SNE Projection')
axes[1].set_xlabel('t-SNE 1')
axes[1].set_ylabel('t-SNE 2')
axes[1].grid(True, alpha=0.3)

# UMAP
umap_reducer = umap.UMAP(n_neighbors=15, min_dist=0.1, random_state=42)
umap_result = umap_reducer.fit_transform(X)
scatter = axes[2].scatter(umap_result[:, 0], umap_result[:, 1], c=y,
                        cmap=colors, s=50, alpha=0.8)
axes[2].set_title('UMAP Projection')
axes[2].set_xlabel('UMAP 1')
axes[2].set_ylabel('UMAP 2')
axes[2].grid(True, alpha=0.3)

plt.tight_layout()
plt.show()

Wir sehen das Vergleichsdiagramm wie folgt:

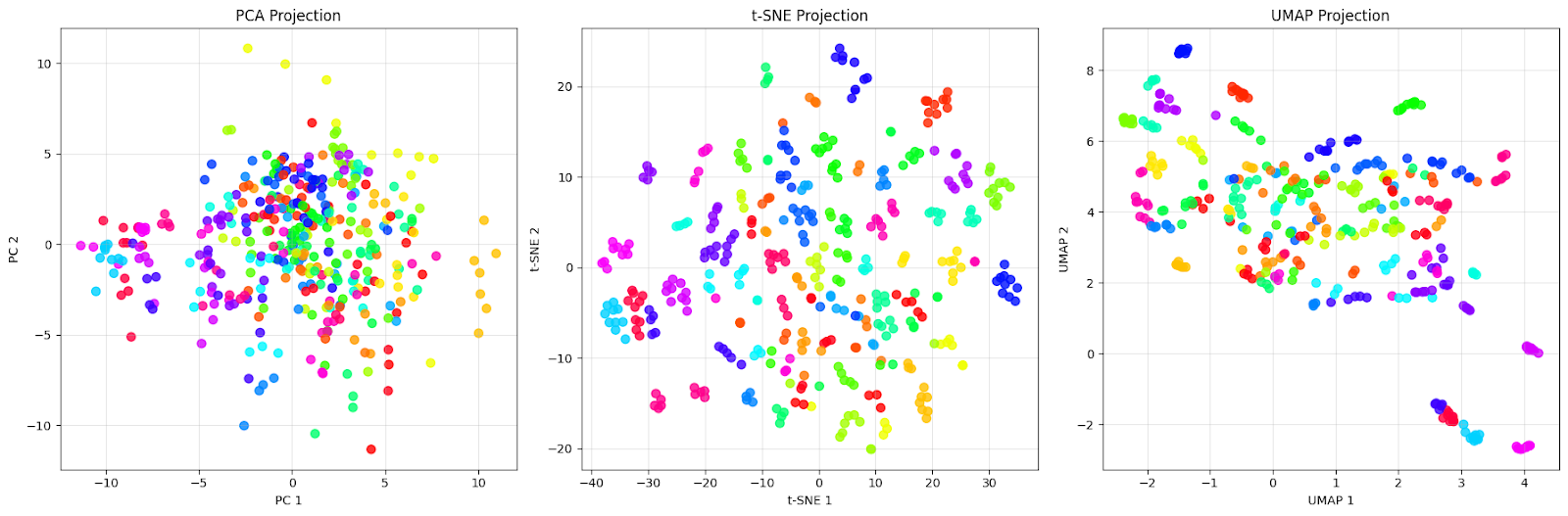
Die PCA-Projektion (links) zeigt eine dichte Cloud, die sich um den Ursprung dreht, mit vielen Überschneidungen zwischen den verschiedenfarbigen Punkten. Genau das erwarten wir von PCA – sie erfasst die Richtungen der maximalen Varianz in den Daten, schafft es aber nicht, die verschiedenen Personen effektiv voneinander zu trennen. Wir können sehen, dass Gesichter von verschiedenen Leuten (unterschiedliche Farben) komplett durcheinander sind, sodass es fast unmöglich ist, bestimmte Gruppen zu erkennen.

Die t-SNE- Projektion (Mitte) zeigt eine Verbesserung mit gut voneinander getrennten Clustern. Jede Farbe (die für eine andere Person steht) bildet eine eigene, kompakte Gruppe mit klaren Grenzen zwischen den verschiedenen Personen. Schau mal, wie t-SNE fast perfekte lokale Gruppierungen macht, bei denen Gesichter derselben Person ganz nah beieinander liegen und von anderen Gruppen weggeschoben werden. Das ist die Stärke von t-SNE: Es ist super darin, lokale Nachbarschaften zu erhalten und visuell unterschiedliche Cluster zu erstellen. 

Die UMAP-Projektion (rechts) geht anders vor. Die Cluster sind zwar im Vergleich zu t-SNE weiter auseinander, aber das zeigt, dass UMAP versucht, sowohl die lokale als auch die globale Struktur zu behalten. Wir können sehen, dass jede Person immer noch erkennbare Gruppen bildet, aber mit mehr Unterschieden innerhalb der Gruppen. Einige Cluster überlappen sich ein bisschen oder liegen näher beieinander, was auf echte Gemeinsamkeiten zwischen diesen Personen hindeuten könnte.

Dieser Vergleich zeigt was Wichtiges: „Besser“ hängt davon ab, was wir erreichen wollen. Wenn wir für die Präsentation oder erste Untersuchung eine möglichst klare visuelle Trennung brauchen, sind die engen Cluster von t-SNE super für diesen Datensatz. Wenn wir aber die Gesamtstruktur der Daten und die Beziehungen zwischen den verschiedenen Gruppen verstehen wollen, ist UMAP mit seiner Erhaltung globaler Beziehungen besser für diesen Datensatz geeignet.

Häufige Probleme mit UMAP und wie man sie löst

Wie bei allen Algorithmen und Techniken gibt's auch bei der Anwendung von UMAP auf echte Daten ein paar Herausforderungen. 

Ich hab mich intensiv damit beschäftigt und hier sind ein paar Probleme, die mir aufgefallen sind und immer wieder auftauchen:

1. Die richtigen Parameter auswählen

Die häufigste Herausforderung ist, die richtigen Werte für „ n_neighbors “ und „ min_dist “ zu finden. Diese Einstellungen beeinflussen die Darstellung ziemlich stark, und es gibt keine Lösung, die für alle passt. 

Der Parameter„n_neighbors“ im „ “ sorgt für ein Gleichgewicht zwischen lokaler und globaler Strukturbeibehaltung. Kleinere Werte (5–15) konzentrieren sich auf die Erhaltung sehr lokaler Nachbarschaften, erfassen feinkörnige Strukturen, können aber größere Muster fragmentieren. Höhere Werte (30–100) zeigen breitere Verbindungsmuster, machen globale Strukturen sichtbar, können aber lokale Details überdecken. 

Der Parameter„min_dist“im „ “ bestimmt, wie dicht die Punkte im niedrigdimensionalen Layout gepackt werden, aber er hat keinen Einfluss auf die hochdimensionale Graphkonstruktion. Werte nahe 0 lassen Punkte dicht packen, was zu optisch kompakten Clustern führt, während Werte nahe 1 die Punkte gleichmäßiger über den Projektionsraum verteilen.

Am besten fängst du mit den Standardwerten an (n_neighbors=15, min_dist=0.1) und passt sie dann an deine Daten an:

• Bei Datensätzen mit klaren, gut voneinander getrennten Clustern können wir kleinere n_neighbors (5-15) nehmen, um die lokale Struktur zu behalten.
• Für Datensätze mit einer eher kontinuierlichen oder hierarchischen Struktur können wir größere n_neighbors (30–100) nehmen, um globale Beziehungen zu erfassen.
• Abnehmend min_dist (in Richtung 0) für eine engere visuelle Clusterbildung in der Projektion
• Erhöhen min_dist (in Richtung 0,5–1,0) für gleichmäßiger verteilte Punkte, die man besser sehen kann

2. Rechenleistung bei großen Datensätzen

UMAP kann bei riesigen Datensätzen (Millionen von Punkten) ziemlich langsam sein, was die interaktive Erkundung echt schwierig macht. Wir können ein paar der folgenden Techniken ausprobieren, um die Leistung zu verbessern:

• Reduzierung der Anzahl der Epochen für eine schnellere Konvergenz: umap.UMAP(n_epochs=200) (Standardwert ist None, was automatisch anhand der Datensatzgröße ausgewählt wird)
• Verwendung einer zufälligen Initialisierung anstelle einer spektralen Initialisierung für sehr große Datensätze: umap.UMAP(init='random')
• Wir nehmen eine Teilstichprobe unserer Daten für die erste Untersuchung und wenden sie dann auf den ganzen Datensatz an.
• Mit dem n_jobs für die parallele Verarbeitung: umap.UMAP(n_jobs=-1)
• Einstellung low_memory=False wenn wir genug RAM haben und schneller rechnen wollen, auch wenn das mehr Speicher braucht
• Mit RAPIDS cuML für die GPU-Beschleunigung auf kompatibler Hardware.
• Für große Datensätze können wir densmap=False (Standard) nehmen, weil DensMAP-Erhaltung mehr Rechenaufwand braucht.

3. Entfernungen in UMAP-Projektionen interpretieren

Anders als bei PCA lassen sich die Abstände in UMAP-Projektionen nicht direkt interpretieren. Punkte, die nah beieinander liegen, sind im ursprünglichen Raum vielleicht gar nicht ähnlich. Um diese Einschränkung zu umgehen, solltest du Folgendes beachten:

• Überprüfe die in UMAP gefundenen Cluster anhand der ursprünglichen Merkmale.
• Nutze UMAP hauptsächlich für die Visualisierung und die Entwicklung von Hypothesen.
• Kombiniere UMAP mit anderen Validierungstechniken, wie zum Beispiel Silhouette-Scores
• Mehr Dimensionen (3D oder 4D) für Analyseaufgaben behalten

4. Reproduzierbarkeitsprobleme

UMAP nutzt eine zufällige Initialisierung, was bei verschiedenen Durchläufen zu unterschiedlichen Ergebnissen führen kann, sodass es schwierig ist, Visualisierungen genau zu reproduzieren. Wir können die Reproduzierbarkeit sicherstellen, indem wir diese Vorgehensweisen befolgen:

• Stell immer den Parameter „ random_state “ ein: umap.UMAP(random_state=42)
• Für kritische Analysen: UMAP mehrmals laufen lassen und nach konsistenten Mustern suchen
• Benutzung des Parameters „ init “, um die Anfangspositionen festzulegen, wenn es auf exakte Reproduzierbarkeit ankommt

5. Umgang mit gemischten Datentypen

Die Standard-Distanzmetrik von UMAP geht von kontinuierlichen numerischen Daten aus, was bei Datensätzen mit kategorialen oder gemischten Merkmalen Probleme machen kann. Bei der Arbeit mit gemischten Datentypen können wir diese Ansätze in Betracht ziehen:

• Kategoriale Variablen richtig vorbereiten (One-Hot-Kodierung oder Einbettung)
• Benutzerdefinierte Distanzmetriken verwenden, die gemischte Datentypen verarbeiten
• Benutzung des Parameters „ metric “ mit Optionen wie „hamming“ für Binärdaten
• UMAP separat auf verschiedene Merkmalstypen anwenden und dann die Erkenntnisse kombinieren

6. Ausreißer, die die Visualisierung verzerren

Extreme Ausreißer können die Hauptdatenverteilung komprimieren, sodass es schwierig wird, die Struktur der meisten Punkte zu erkennen. Ein paar Techniken, die wir nutzen können, um das zu schaffen, sind:

• Identifizieren und Entfernen von extremen Ausreißern vor der Anwendung von UMAP
• Robuste Skalierung anstelle von Standard-Skalierung verwenden
• Anpassen des Parameters „ local_connectivity “, damit er robuster gegenüber Ausreißern ist
• Mit der Transformationsmethode von UMAP Ausreißer nach der Anpassung an saubere Daten projizieren

Diese Liste ist zwar nicht komplett, deckt aber die häufigsten Probleme ab, die bei der Arbeit mit UMAP auftauchen. Wenn wir diese Probleme und ihre Lösungen verstehen, können wir UMAP optimal nutzen.

Fazit

In diesem Tutorial haben wir uns angesehen, wie UMAP sowohl theoretisch als auch praktisch funktioniert, es auf echte Daten angewendet, mit anderen Methoden verglichen und uns mit typischen Problemen beschäftigt. Das Wichtigste ist, dass UMAP gut für die explorative Datenanalyse bei komplexen, hochdimensionalen Datensätzen ist, weil es die lokale und globale Struktur gut im Gleichgewicht hält.

Um dein Fachwissen über Techniken zur Dimensionsreduktion zu vertiefen, solltest du dir unsere Kurs „Dimensionsreduktion in Python” an, wo du praktische Erfahrungen mit UMAP und anderen Techniken wie PCA und t-SNE sammeln kannst. Für einen umfassenderen Überblick darüber, wie Dimensionsreduktion in Machine-Learning-Workflows passt, schau dir den Beitrag „Machine Learning Scientist with Python“ an. Machine Learning Scientist mit Python lehrt Ihnen sowohl überwachte als auch unüberwachte Lerntechniken und hilft Ihnen dabei, End-to-End-Lösungen für reale Datenherausforderungen zu entwickeln.