Entendendo o UMAP: Um guia completo sobre redução de dimensionalidade

Muitas vezes a gente encontra conjuntos de dados com centenas ou até milhares de características em problemas de machine learning, e essa escala geralmente traz desafios para visualizar e analisar os dados de forma significativa. Os métodos tradicionais de plotagem só conseguem mostrar duas ou três dimensões de uma vez, o que torna quase impossível entender a estrutura dos dados de alta dimensão. É aí que as técnicas de redução de dimensionalidade, como o UMAP (Aproximação e Projeção Uniformes de Variedades), entram em cena.

Com o tempo, o UMAP virou um método super útil pra visualizar conjuntos de dados complexos em várias áreas. Este tutorial vai te mostrar tudo o que você precisa saber sobre o UMAP, desde o básico até a implementação prática e os desafios comuns, ajudando você a começar a usar essa técnica nos seus projetos a partir de agora.

O que é o UMAP?

O UMAP é um algoritmo de redução de dimensionalidade não linear que projeta dados de alta dimensionalidade em um espaço de dimensionalidade inferior (normalmente 2D ou 3D), preservando a estrutura essencial dos dados. UMAP significa Uniform Manifold Approximation and Projection (Aproximação e Projeção Uniformes de Variedades) e baseia-se na aprendizagem de variedades e na análise topológica de dados.

Outros métodos de redução de dimensionalidade, como o t-SNE, são bons em preservar vizinhanças locais, mas acabam distorcendo as relações globais. A principal vantagem do UMAP é que ele consegue um equilíbrio entre as comunidades locais e as relações globais. Ele assume que os dados estão em uma variedade Riemanniana e que essa variedade pode ser modelada localmente com uma estrutura topológica difusa. Essa base matemática permite que o UMAP crie visualizações mais significativas, onde pontos de dados parecidos se juntam, mantendo a topologia geral do conjunto de dados.

O algoritmo funciona construindo uma representação gráfica de alta dimensão dos dados e, em seguida, otimizando um gráfico de baixa dimensão para que seja o mais parecido possível em termos estruturais. Além da visualização, o UMAP é útil como etapa de pré-processamento para algoritmos de agrupamento ou mesmo como uma técnica geral de redução de dimensionalidade não linear para pipelines de machine learning.

Como funciona o UMAP

Vamos dividir o processo em várias etapas importantes para entender como o UMAP funciona. A teoria matemática completa envolve conceitos avançados de topologia e análise de dados topológicos, então, para este tutorial, vamos adotar uma abordagem intuitiva ao algoritmo central.

Passo 1: Construindo o gráfico de alta dimensão

O UMAP começa construindo um gráfico ponderado que representa as relações no espaço de alta dimensão. Para cada ponto de dados, ele identifica seus k vizinhos mais próximos (onde k é um parâmetro que podemos ajustar). Mas, diferente dos gráficos k-NN simples, o UMAP usa uma abordagem probabilística. Ele calcula a probabilidade de dois pontos estarem conectados com base na distância entre eles, usando uma aproximação suave que depende da densidade local ao redor de cada ponto.

A ideia principal aqui é que o UMAP se adapta à estrutura local dos nossos dados. Em regiões densas, os pontos precisam estar bem próximos para serem considerados vizinhos, enquanto em regiões esparsas, o algoritmo amplia seu raio de busca. 

Esse comportamento adaptativo é controlado pela fórmula:

p(i,j) = exp(-(d(xi, xj) - ρi) / σi)

Onde d(xi, xj) é a distância entre os pontos, ρi é a distância até o vizinho mais próximo e σi é um fator de escala calculado para cada ponto.

Passo 2: Criando uma representação topológica difusa

O UMAP então transforma essas distribuições de probabilidade locais numa estrutura topológica difusa a partir da análise de dados topológicos. Ele simetriza o gráfico combinando as probabilidades de ambas as direções:

p(i,j) = p(i|j) + p(j|i) - p(i|j) * p(j|i)

Isso cria o que chamamos de conjunto simplicial difuso, que capta a estrutura múltipla dos dados de alta dimensão.

Passo 3: Otimizando a representação de baixa dimensão

A etapa final envolve encontrar uma representação de baixa dimensão que preserve a estrutura topológica difusa. O UMAP começa com pontos no espaço de baixa dimensão (usando uma incorporação espectral) e, em seguida, usa o gradiente descendente para minimizar a entropia cruzada entre as representações topológicas difusas de alta e baixa dimensão.

A otimização usa forças de atração para juntar pontos que devem estar próximos (com base na estrutura de alta dimensão) e forças de repulsão para separar pontos que devem estar distantes. Essa dinâmica de empurrar e puxar cria as visualizações típicas, onde os clusters ficam bem separados, mas mantêm a estrutura interna.

Aplicações práticas do UMAP

O UMAP tem aplicações em vários campos onde é útil entender dados de alta dimensão. 

Algumas dessas aplicações no mundo real incluem:

• Genômica de célula única e bioinformática: Na pesquisa genômica, o UMAP virou o padrão para visualizar dados de sequenciamento de RNA de célula única. Os pesquisadores usam isso pra identificar tipos de células, acompanhar trajetórias de desenvolvimento e entender a progressão de doenças. Ao reduzir milhares de medições de expressão gênica a um gráfico 2D, o UMAP mostra populações celulares diferentes e suas relações, o que seria impossível de ver nos dados brutos.
• Processamento de linguagem natural: Os dados de texto, quando convertidos em incorporações de alta dimensão, podem ser visualizados usando o UMAP para entender as relações semânticas. É normalmente usado pra visualizar embeddings de palavras, clusters de documentos e pra depurar modelos de linguagem, mostrando como diferentes conceitos se relacionam entre si no espaço de embedding.
• Visão computacional e análise de imagens: O UMAP ajuda a visualizar representações de características aprendidas por redes neurais, facilitando a compreensão dos padrões que o modelo aprendeu. Também é usado em sistemas de reconhecimento facial para visualizar como os rostos se agrupam com base em suas características e em imagens médicas para identificar casos semelhantes ou anomalias.
• Exploração de dados e deteção de valores atípicos: O UMAP ajuda a revelar padrões ocultos e a detectar valores atípicos em conjuntos de dados complexos, projetando-os em um espaço visual interpretável. Essa abordagem visual para detectar valores atípicos é super útil quando os métodos estatísticos tradicionais têm dificuldade com interações de alta dimensão.
• Segmentação de clientes e análise de mercado: As equipes de marketing usam o UMAP para visualizar os padrões de comportamento dos clientes com base em vários recursos, como histórico de compras, dados demográficos e métricas de engajamento. Isso ajuda a identificar segmentos distintos de clientes e a entender as relações entre os diferentes grupos.
• Descoberta de medicamentos: Pesquisadores farmacêuticos usam o UMAP para visualizar espaços de compostos químicos, ajudando-os a identificar candidatos promissores a medicamentos, observando quais compostos se agrupam perto de medicamentos eficazes conhecidos e, ao mesmo tempo, distantes de compostos tóxicos.

Agora que entendemos o conceito, os fundamentos matemáticos e as aplicações práticas do UMAP, vamos passar para a implementação.

Implementação do UMAP em Python

Vamos implementar o UMAP em um conjunto de dados do mundo real para ver como ele funciona na prática. Vamos usar o conjunto de dados Olivetti Faces, que tem imagens em tons de cinza de rostos de 40 pessoas diferentes. O conjunto de dados Olivetti pode ser baixado do Kaggle ou pela biblioteca Python scikit-learn.

O conjunto de dados Olivetti Faces tem:

• 400 imagens em escala de cinza (64x64 pixels = 4096 dimensões)
• 40 pessoas diferentes
• 10 fotos por pessoa (expressões diferentes, condições de iluminação)

Isso é perfeito para o UMAP, porque esperamos que as imagens da mesma pessoa se agrupem, mesmo com variações na expressão e na iluminação.

Passo 1: Importar bibliotecas e carregar os dados

Primeiro, vamos importar as bibliotecas necessárias e carregar nosso conjunto de dados:

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import matplotlib.cm as cm
from sklearn.datasets import fetch_olivetti_faces
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
import umap
import warnings
warnings.filterwarnings('ignore')

# Load the Olivetti faces dataset
faces = fetch_olivetti_faces(shuffle=True, random_state=42)
X = faces.data
y = faces.target

print(f"Dataset shape: {X.shape}")
print(f"Number of individuals: {len(np.unique(y))}")
print(f"Number of images per individual: {X.shape[0] // len(np.unique(y))}")

# Display sample faces
fig, axes = plt.subplots(2, 5, figsize=(12, 6))
for i, ax in enumerate(axes.flat):
   ax.imshow(X[i].reshape(64, 64), cmap='gray')
   ax.set_title(f'Person {y[i]}')
   ax.axis('off')
plt.suptitle('Sample Faces from the Dataset')
plt.tight_layout()
plt.show()

A partir do código acima, podemos visualizar o conjunto de dados da seguinte forma:

Passo 2: Aplique o UMAP com os parâmetros padrão

O conjunto de dados Olivetti faces já vem pré-normalizado com valores de pixel entre 0 e 1, então podemos aplicar o UMAP direto:

# Create UMAP instance with default parameters
reducer = umap.UMAP(random_state=42)

# Fit and transform the data
embedding = reducer.fit_transform(X)

# Create a custom colormap for 40 distinct classes
colors = cm.get_cmap('hsv', 40)  

# Create visualization
plt.figure(figsize=(12, 10))
scatter = plt.scatter(embedding[:, 0], embedding[:, 1], c=y,
                    cmap=colors, s=50, alpha=0.8, edgecolors='black', linewidth=0.5)
plt.colorbar(scatter, label='Person ID', ticks=np.arange(0, 40, 5))
plt.title('UMAP Projection of Olivetti Faces (Default Parameters)')
plt.xlabel('UMAP 1')
plt.ylabel('UMAP 2')
plt.grid(True, alpha=0.3)
plt.show()

A gente vê um gráfico de dispersão colorido como uma visualização UMAP:

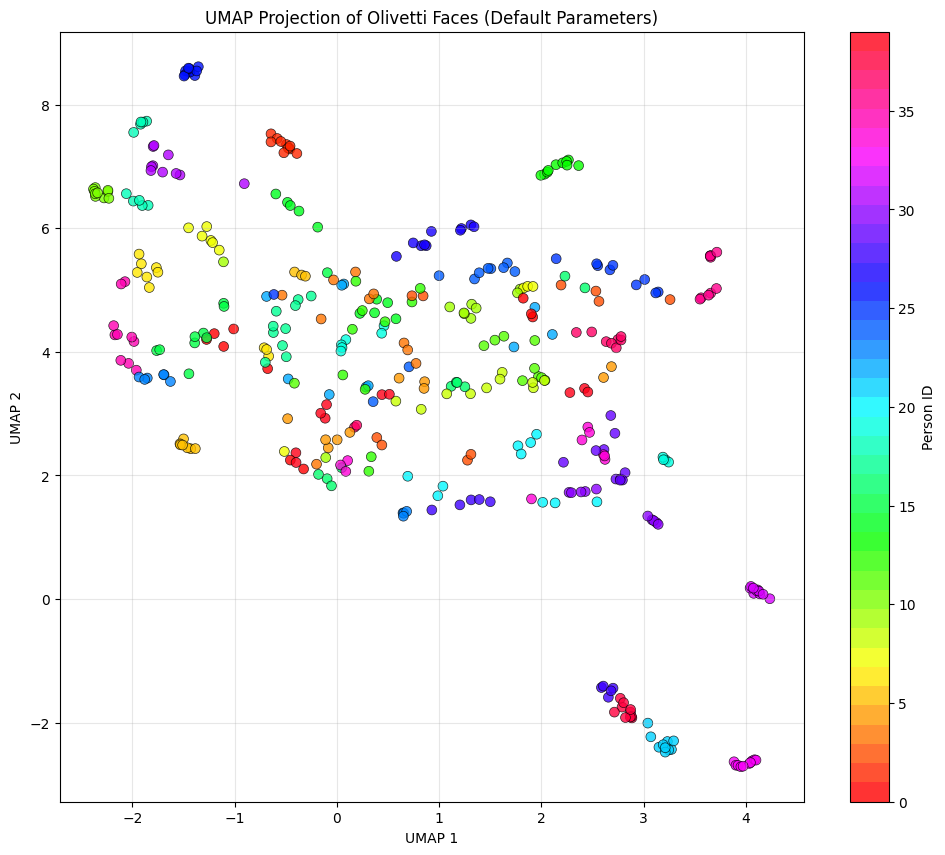
Aqui estão algumas coisas a serem observadas para entender melhor o diagrama:

• Cada ponto representa uma imagem facial.
• As cores representam pessoas diferentes (Identificação da pessoa 0–39)
• Proximidade significa semelhança: Pontos próximos uns dos outros são faces que o UMAP considera semelhantes no espaço de 4096 dimensões.

Embora isso não aconteça na vida real, o ideal seria que todas as 10 imagens da mesma pessoa (mesma cor) ficassem juntas. Na imagem, a gente vê algumas cores parecidas agrupadas quando criamos o UMAP usando os parâmetros padrão.

Passo 3: Explore os principais parâmetros do UMAP

O UMAP tem vários parâmetros importantes que controlam o seu comportamento. Vamos ver como eles afetam os resultados:

# Create subplots for different parameter settings
fig, axes = plt.subplots(2, 3, figsize=(18, 12))
axes = axes.ravel()

# Different parameter configurations
param_configs = [
   {'n_neighbors': 5, 'min_dist': 0.1},
   {'n_neighbors': 15, 'min_dist': 0.1},
   {'n_neighbors': 50, 'min_dist': 0.1},
   {'n_neighbors': 15, 'min_dist': 0.0},
   {'n_neighbors': 15, 'min_dist': 0.5},
   {'n_neighbors': 15, 'min_dist': 0.99}
]

# Apply UMAP with different parameters
for idx, params in enumerate(param_configs):
   reducer = umap.UMAP(random_state=42, **params)
   embedding = reducer.fit_transform(X_scaled)
  
   ax = axes[idx]
   scatter = ax.scatter(embedding[:, 0], embedding[:, 1], c=y,
                       cmap='tab20', s=30, alpha=0.8)
   ax.set_title(f"n_neighbors={params['n_neighbors']}, "
                f"min_dist={params['min_dist']}")
   ax.set_xlabel('UMAP 1')
   ax.set_ylabel('UMAP 2')
   ax.grid(True, alpha=0.3)

plt.tight_layout()
plt.show()

A visualização da saída é assim:

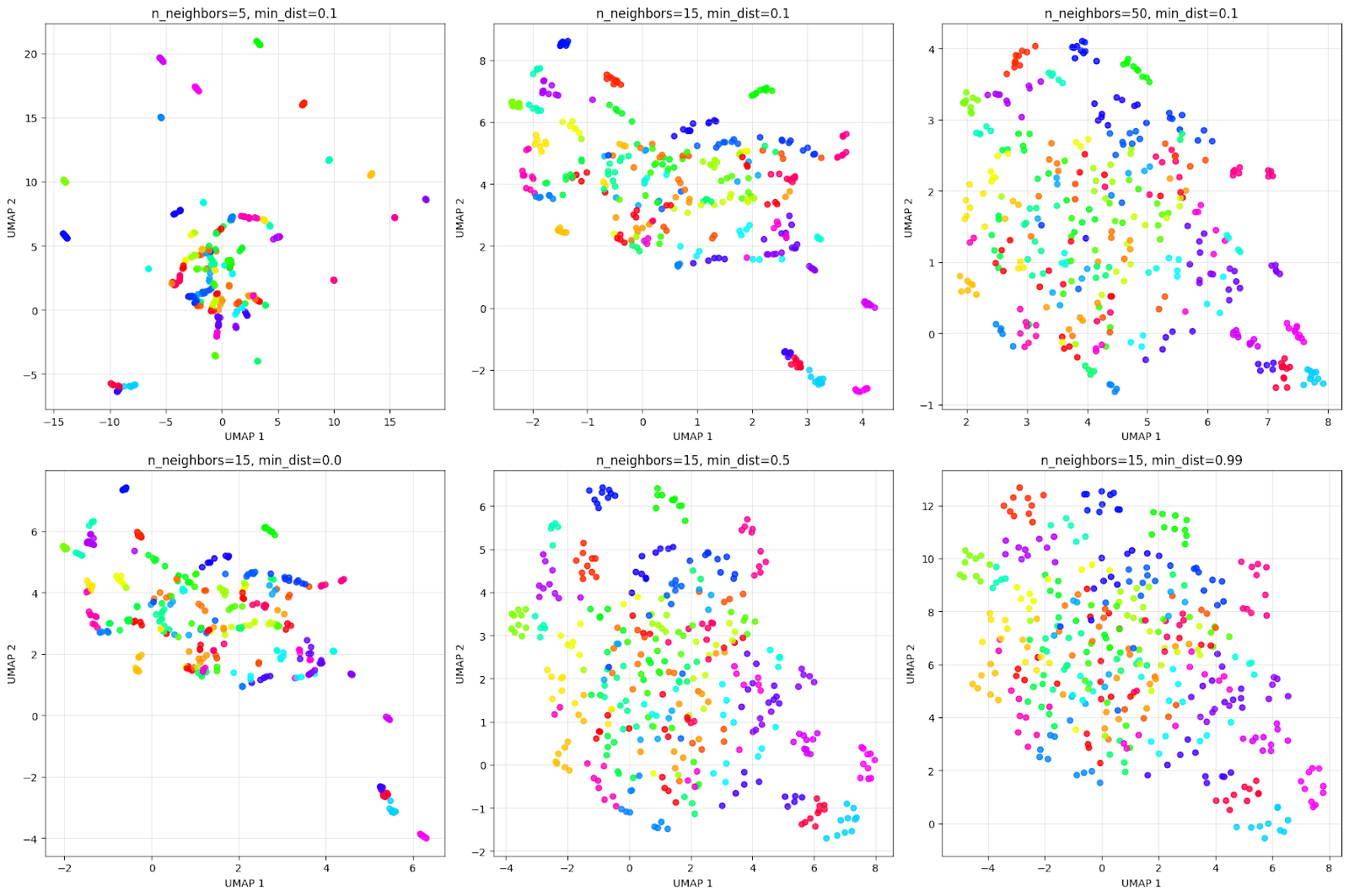
A grade acima mostra como os parâmetros afetam a visualização. Pensando no efeito da linha superior de n_neighbors:

• n_neighbors=5: Visão bem local, cria muitos grupos pequenos e compactos.
• n_neighbors=15: Visão equilibrada, oferece uma boa combinação entre estrutura local e global.
• n_neighbors=50: Visão global, foca na estrutura geral, podendo juntar pessoas parecidas.

Olha só a linha de baixo do efeito min_dist:

• min_dist=0.0: Os pontos estão bem próximos, como dá pra ver no grid. Isso cria aglomerados bem compactos e densos.
• min_dist=0.5: Espaçamento médio, resultando em grupos mais espalhados.
• min_dist=0.99: O espaçamento máximo faz com que os pontos fiquem distribuídos de maneira uniforme, mas perde a estrutura do agrupamento.

É sempre uma boa ideia testar esses parâmetros para conseguir o melhor resultado de agrupamento para o problema em questão.

Alternativas ao UMAP para redução de dimensionalidade

Vamos continuar nosso exemplo com o conjunto de dados Olivetti para comparar UMAP com PCA e t-SNE e entender suas diferenças:

from sklearn.decomposition import PCA
from sklearn.manifold import TSNE

# Create figure with subplots
fig, axes = plt.subplots(1, 3, figsize=(18, 6))

colors = cm.get_cmap('hsv', 40)

# PCA
pca = PCA(n_components=2, random_state=42)
pca_result = pca.fit_transform(X)
axes[0].scatter(pca_result[:, 0], pca_result[:, 1], c=y,
               cmap=colors, s=50, alpha=0.8)
axes[0].set_title('PCA Projection')
axes[0].set_xlabel('PC 1')
axes[0].set_ylabel('PC 2')
axes[0].grid(True, alpha=0.3)

# t-SNE
tsne = TSNE(n_components=2, random_state=42, perplexity=30)
tsne_result = tsne.fit_transform(X)
axes[1].scatter(tsne_result[:, 0], tsne_result[:, 1], c=y,
               cmap=colors, s=50, alpha=0.8)
axes[1].set_title('t-SNE Projection')
axes[1].set_xlabel('t-SNE 1')
axes[1].set_ylabel('t-SNE 2')
axes[1].grid(True, alpha=0.3)

# UMAP
umap_reducer = umap.UMAP(n_neighbors=15, min_dist=0.1, random_state=42)
umap_result = umap_reducer.fit_transform(X)
scatter = axes[2].scatter(umap_result[:, 0], umap_result[:, 1], c=y,
                        cmap=colors, s=50, alpha=0.8)
axes[2].set_title('UMAP Projection')
axes[2].set_xlabel('UMAP 1')
axes[2].set_ylabel('UMAP 2')
axes[2].grid(True, alpha=0.3)

plt.tight_layout()
plt.show()

Vamos ver o gráfico comparativo abaixo:

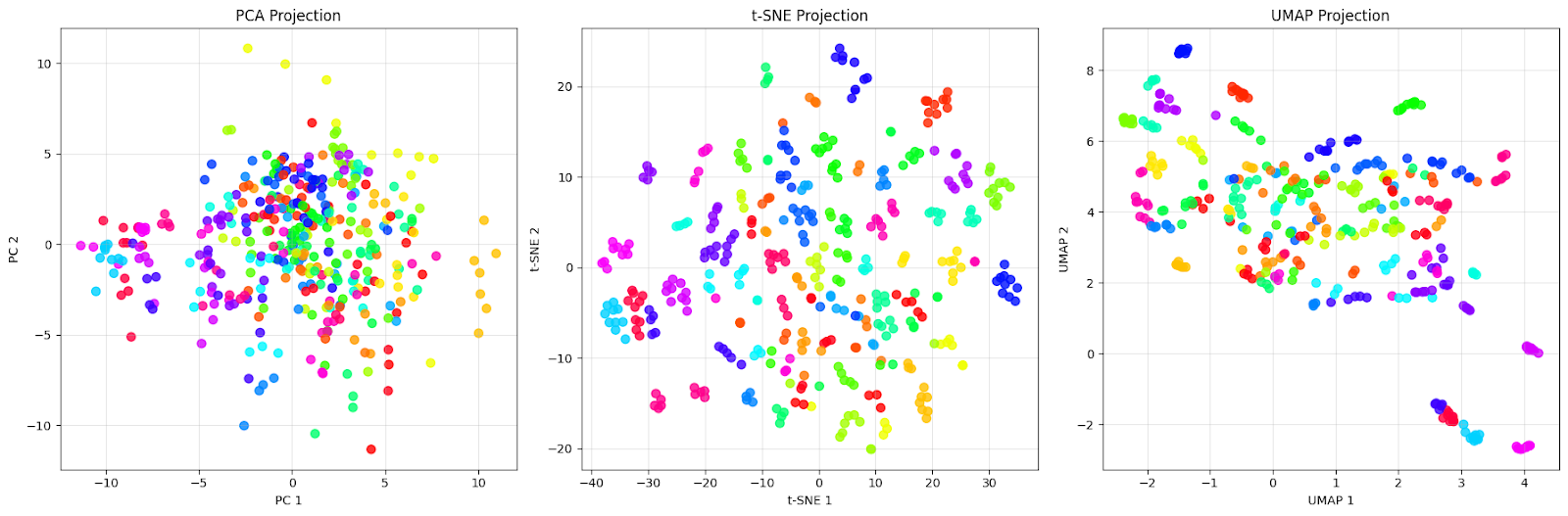
A projeção PCA (à esquerda) mostra uma nuvem densa de pontos concentrados em torno da origem, com uma grande sobreposição entre pontos de cores diferentes. É exatamente isso que esperamos da PCA — ela capta as direções de variação máxima nos dados, mas não consegue separar as diferentes pessoas de forma eficaz. Dá pra ver que os rostos de pessoas diferentes (cores diferentes) estão completamente misturados, o que torna quase impossível identificar grupos distintos.

A projeção t-SNE (no meio) mostra uma melhora com grupos bem separados. Cada cor (que representa uma pessoa diferente) forma um grupo distinto e compacto, com limites claros entre os diferentes indivíduos. Observe como o t-SNE cria agrupamentos locais quase perfeitos, nos quais os rostos da mesma pessoa são colocados muito próximos uns dos outros, enquanto são afastados de outros grupos. Essa é a força do t-SNE: ele é ótimo em preservar vizinhanças locais e criar agrupamentos visualmente distintos. 

A projeção UMAP (à direita) usa uma abordagem diferente. Embora os clusters estejam mais espalhados em comparação com o t-SNE, isso mostra como o UMAP tenta manter tanto a estrutura local quanto a global. A gente vê que cada pessoa ainda forma grupos reconhecíveis, mas com mais variação interna. Alguns grupos mostram uma pequena sobreposição ou estão mais próximos uns dos outros, o que pode indicar semelhanças reais entre esses indivíduos.

Essa comparação mostra uma coisa importante: “melhor” depende do nosso objetivo. Se precisarmos da separação visual mais clara possível para apresentação ou exploração inicial, os clusters compactos do t-SNE são excelentes para este conjunto de dados. Mas, se a gente quiser entender a estrutura geral dos dados e como os diferentes grupos se relacionam entre si, a preservação das relações globais do UMAP torna-o mais adequado para este conjunto de dados.

Desafios comuns com o UMAP e como resolvê-los

Como acontece com todos os algoritmos e técnicas, a gente enfrenta vários desafios ao aplicar o UMAP a dados do mundo real. 

Tendo trabalhado bastante nisso, aqui estão alguns desafios que percebi que sempre aparecem:

1. Escolhendo os parâmetros certos

O desafio mais comum é escolher valores adequados para n_neighbors e min_dist. Esses parâmetros afetam bastante a visualização, e não tem uma solução única que sirva para todos. 

O parâmetron_neighbors equilibra a preservação da estrutura local e global. Valores menores (5-15) focam em preservar bairros bem locais, capturando uma estrutura bem detalhada, mas podendo fragmentar padrões maiores. Valores maiores (30-100) destacam padrões de conectividade mais amplos, mostrando a estrutura global, mas podem esconder detalhes locais. 

O parâmetromin_dist controla o quanto os pontos ficam compactados no layout de baixa dimensão, mas não afeta a construção do gráfico de alta dimensão. Valores próximos a 0 permitem que os pontos sejam agrupados de forma mais densa, criando aglomerados visualmente compactos, enquanto valores próximos a 1 espalham os pontos de forma mais uniforme pelo espaço de projeção.

A melhor maneira é começar com os valores padrão (n_neighbors=15, min_dist=0.1) e ajustar de acordo com as características dos seus dados:

• Para conjuntos de dados com clusters claros e bem separados, podemos usar vizinhos menores. n_neighbors (5-15) para manter a estrutura local.
• Para conjuntos de dados com uma estrutura mais contínua ou hierárquica, podemos usar vizinhos maiores. n_neighbors (30-100) para capturar relações globais.
• Diminuindo min_dist (em direção a 0) para um agrupamento visual mais preciso na projeção
• Aumentando min_dist (para 0,5-1,0) para pontos distribuídos de forma mais uniforme e mais fáceis de distinguir visualmente

2. Desempenho computacional em grandes conjuntos de dados

O UMAP pode ser lento em conjuntos de dados muito grandes (milhões de pontos), dificultando a exploração interativa. A gente pode tentar algumas dessas técnicas abaixo para melhorar o desempenho:

• Reduzindo o número de épocas para uma convergência mais rápida: umap.UMAP(n_epochs=200) (o padrão é None, que seleciona automaticamente com base no tamanho do conjunto de dados)
• Usando inicialização aleatória em vez de espectral para conjuntos de dados muito grandes: umap.UMAP(init=“random”)
• Fazendo uma subamostragem dos nossos dados para uma exploração inicial e, em seguida, aplicando-a ao conjunto de dados completo.
• Usando o n_jobs para processamento paralelo: umap.UMAP(n_jobs=-1)
• Configurando low_memory=False se tivermos RAM suficiente e quisermos um cálculo mais rápido, mesmo que isso consuma mais memória.
• Usando RAPIDS cuML para aceleração por GPU em hardware compatível.
• Para conjuntos de dados grandes, podemos usar densmap=False (o padrão), já que a preservação DensMAP adiciona sobrecarga computacional.

3. Interpretando distâncias em projeções UMAP

Ao contrário da PCA, as distâncias nas projeções UMAP não têm uma interpretação direta. Pontos que parecem próximos podem não ser parecidos no espaço original. Para resolver essa limitação, é importante:

• Valide os clusters encontrados no UMAP usando as características originais.
• Use o UMAP principalmente para visualização e geração de hipóteses.
• Combine o UMAP com outras técnicas de validação, como pontuações de silhueta
• Guarde mais dimensões (3D ou 4D) para tarefas de análise

4. Problemas de reprodutibilidade

O UMAP usa inicialização aleatória, o que pode levar a resultados diferentes entre as execuções, dificultando a reprodução de visualizações exatas. A gente pode garantir a reprodutibilidade seguindo essas práticas:

• Sempre definindo o parâmetro random_state: umap.UMAP(random_state=42)
• Para análises críticas, execute o UMAP várias vezes e procure padrões consistentes.
• Usando o parâmetro init para especificar as posições iniciais se for necessária uma reprodutibilidade exata

5. Como lidar com tipos de dados misturados

A métrica de distância padrão do UMAP assume dados numéricos contínuos, o que pode ser problemático para conjuntos de dados com características categóricas ou mistas. Ao trabalhar com tipos de dados mistos, podemos pensar nessas abordagens:

• Pré-processar variáveis categóricas da maneira certa (codificação one-hot ou incorporação)
• Usando métricas de distância personalizadas que lidam com tipos de dados mistos
• Usando o parâmetro ` metric ` com opções como `'hamming'` para dados binários
• Aplicando o UMAP separadamente a diferentes tipos de recursos e, em seguida, juntando as ideias

6. Valores atípicos que distorcem a visualização

Valores extremos podem comprimir a distribuição dos dados principais, dificultando a visualização da estrutura na maioria dos pontos. Algumas técnicas que podemos usar para superar isso são:

• Identificando e removendo valores extremos antes de aplicar o UMAP
• Usando escala robusta em vez de escala padrão
• Ajustando o parâmetro “ local_connectivity ” para ficar mais resistente a valores atípicos
• Usando o método de transformação do UMAP para projetar outliers após o ajuste em dados limpos

Embora essa lista não seja completa, ela cobre os problemas mais comuns que a gente encontra ao trabalhar com o UMAP. Entender essas questões e suas soluções vai nos ajudar a aproveitar ao máximo o UMAP.

Conclusão

Neste tutorial, a gente viu como o UMAP funciona, tanto na teoria quanto na prática, colocamos em ação com dados reais, comparamos com outros métodos e falamos sobre os desafios mais comuns. A principal conclusão é que a capacidade do UMAP de equilibrar a preservação da estrutura local e global o torna útil para a análise exploratória de dados ao lidar com conjuntos de dados complexos e de alta dimensão.

Para aprofundar seus conhecimentos sobre técnicas de redução de dimensionalidade, considere explorar nosso Redução de dimensionalidade em Python, onde você vai ganhar experiência prática com o UMAP junto com outras técnicas, como PCA e t-SNE. Para uma visão mais ampla sobre como a redução de dimensionalidade se encaixa nos fluxos de trabalho de machine learning, o Cientista de machine learning com Python O programa ensina técnicas de aprendizado supervisionado e não supervisionado, ajudando você a criar soluções completas para desafios de dados do mundo real.