Comprendre l'UMAP : Guide complet sur la réduction de dimensionnalité

Dans le domaine de l'apprentissage automatique, nous sommes fréquemment confrontés à des ensembles de données comportant des centaines, voire des milliers de caractéristiques, ce qui rend souvent difficile la visualisation et l'analyse pertinentes des données. Les méthodes traditionnelles de graphiques ne peuvent afficher que deux ou trois dimensions à la fois, ce qui rend presque impossible la compréhension de la structure des données à haute dimension. C'est là que les techniques de réduction de dimensionnalité telles que l'UMAP (Uniform Manifold Approximation and Projection) s'avèrent utiles.

Au fil du temps, l'UMAP est devenue une méthode incontournable pour visualiser des ensembles de données complexes dans divers domaines. Ce tutoriel vous guidera à travers tout ce que vous devez savoir sur UMAP, depuis ses fondements jusqu'à sa mise en œuvre pratique et les défis courants, vous aidant ainsi à commencer à utiliser cette technique dans vos projets dès maintenant.

Qu'est-ce que l'UMAP ?

UMAP est un algorithme de réduction de dimensionnalité non linéaire qui projette des données à haute dimensionnalité dans un espace à plus faible dimensionnalité (généralement 2D ou 3D) tout en conservant la structure essentielle des données. UMAP signifie « Uniform Manifold Approximation and Projection » (approximation et projection uniformes de variétés) et repose sur l'apprentissage des variétés et l'analyse topologique des données.

D'autres méthodes de réduction de dimensionnalité, telles que t-SNE, sont efficaces pour préserver les voisinages locaux, mais finissent par déformer les relations globales. Le principal avantage de l'UMAP est qu'il établit un équilibre entre les quartiers locaux et les relations mondiales. Il suppose que les données se trouvent sur une variété riemannienne et que cette variété peut être modélisée localement avec une structure topologique floue. Cette base mathématique permet à UMAP de créer des visualisations plus pertinentes, dans lesquelles les points de données similaires sont regroupés tout en conservant la topologie globale de l'ensemble de données.

L'algorithme fonctionne en construisant une représentation graphique haute dimension des données, puis en optimisant un graphique basse dimension afin qu'il soit aussi similaire que possible sur le plan structurel. Outre la visualisation, UMAP est utile comme étape de prétraitement pour les algorithmes de regroupement ou même comme technique générale de réduction de dimensionnalité non linéaire pour les pipelines d'apprentissage automatique.

Fonctionnement de l'UMAP

Nous allons décomposer le processus en plusieurs étapes clés afin de comprendre le fonctionnement de l'UMAP. La théorie mathématique complète implique des concepts avancés issus de la topologie et de l'analyse topologique des données. Par conséquent, dans le cadre de ce tutoriel, nous adopterons une approche intuitive de l'algorithme de base.

Étape 1 : Construction du graphe à haute dimension

UMAP commence par construire un graphe pondéré qui représente les relations dans l'espace à haute dimension. Pour chaque point de données, il identifie ses k voisins les plus proches (où k est un paramètre que nous pouvons ajuster). Cependant, contrairement aux graphiques k-NN simples, UMAP utilise une approche probabiliste. Il calcule la probabilité que deux points soient connectés en fonction de leur distance, en utilisant une approximation lisse qui dépend de la densité locale autour de chaque point.

L'idée principale ici est que l'UMAP s'adapte à la structure locale de nos données. Dans les régions denses, les points doivent être très proches pour être considérés comme voisins, tandis que dans les régions clairsemées, l'algorithme élargit son rayon de recherche. 

Ce comportement adaptatif est régi par la formule suivante :

p(i,j) = exp(-(d(xi, xj) - ρi) / σi)

Où d(xi, xj) est la distance entre les points, ρi est la distance au voisin le plus proche et σi est un facteur d'échelle calculé pour chaque point.

Étape 2 : Création d'une représentation topologique floue

UMAP convertit ensuite ces distributions de probabilité locales en une structure topologique floue à partir de l'analyse des données topologiques. Il symétrise le graphique en combinant les probabilités des deux directions :

p(i,j) = p(i|j) + p(j|i) - p(i|j) * p(j|i)

Cela crée ce que l'on appelle un ensemble simplicial flou, qui capture la structure multiple des données à haute dimension.

Étape 3 : Optimisation de la représentation à faible dimension

La dernière étape consiste à trouver une représentation de faible dimension qui préserve la structure topologique floue. UMAP initialise les points dans l'espace à faible dimension (à l'aide d'un encodage spectral), puis utilise la descente de gradient pour minimiser l'entropie croisée entre les représentations topologiques floues à haute et à faible dimension.

L'optimisation utilise des forces d'attraction pour rapprocher les points qui devraient être proches (sur la base de la structure à haute dimension) et des forces de répulsion pour éloigner les points qui devraient être distants. Cette dynamique de tension et d'attraction crée des visualisations caractéristiques où les grappes sont bien séparées tout en conservant leur structure interne.

Applications pratiques de l'UMAP

UMAP trouve des applications dans de nombreux domaines où la compréhension des données à haute dimension est utile. 

Certaines de ces applications concrètes comprennent :

• Génomique unicellulaire et bio-informatique: Dans le domaine de la recherche génomique, UMAP est devenu la norme pour la visualisation des données de séquençage d'ARN unicellulaire. Les chercheurs l'utilisent pour identifier les types de cellules, suivre les trajectoires de développement et comprendre la progression des maladies. En réduisant des milliers de mesures d'expression génétique à un graphique en 2D, UMAP met en évidence des populations cellulaires distinctes et leurs relations, ce qui serait impossible à observer dans les données brutes.
• Traitement du langage naturel: Les données textuelles, lorsqu'elles sont converties en intégrations à haute dimension, peuvent être visualisées à l'aide de l'UMAP afin de comprendre les relations sémantiques. Il est couramment utilisé pour visualiser les plongements de mots, les grappes de documents et pour déboguer les modèles linguistiques en montrant comment différents concepts sont liés les uns aux autres dans l'espace de plongement.
• Vision par ordinateur et analyse d'images: UMAP permet de visualiser les représentations des caractéristiques apprises par les réseaux neuronaux, ce qui facilite la compréhension des modèles appris par le modèle. Il est également utilisé dans les systèmes de reconnaissance faciale pour visualiser comment les visages se regroupent en fonction de leurs caractéristiques, ainsi que dans l'imagerie médicale pour identifier des cas similaires ou des anomalies.
• Exploration des données et détection des valeurs aberrantes: UMAP contribue à révéler des modèles cachés et à détecter des valeurs aberrantes dans des ensembles de données complexes en les projetant dans un espace visuel interprétable. Cette approche visuelle de la détection des valeurs aberrantes est particulièrement utile lorsque les méthodes statistiques traditionnelles rencontrent des difficultés avec les interactions à haute dimension.
• Segmentation de la clientèle et analyse de marché: Les équipes marketing utilisent UMAP pour visualiser les modèles de comportement des clients en fonction de multiples caractéristiques telles que l'historique des achats, les données démographiques et les indicateurs d'engagement. Cela permet d'identifier des segments de clientèle distincts et de comprendre les relations entre les différents groupes.
• Découverte de médicaments: Les chercheurs pharmaceutiques utilisent UMAP pour visualiser les espaces des composés chimiques, ce qui les aide à identifier les candidats médicaments prometteurs en identifiant les composés qui se regroupent à proximité des médicaments efficaces connus tout en étant éloignés des composés toxiques.

Maintenant que nous avons compris le concept, les fondements mathématiques et les applications pratiques de l'UMAP, passons à la mise en œuvre.

Mise en œuvre de l'UMAP en Python

Mettons en œuvre UMAP sur un ensemble de données réelles afin d'observer son fonctionnement dans la pratique. Nous utiliserons l'ensemble de données Olivetti Faces, qui contient des images en niveaux de gris représentant les visages de 40 personnes différentes. L'ensemble de données Olivetti peut être téléchargé depuis Kaggle ou via la bibliothèque Python scikit-learn.

L'ensemble de données Olivetti Faces contient :

• 400 images en niveaux de gris (64 x 64 pixels = 4096 dimensions)
• Quarante personnes différentes
• 10 images par personne (différentes expressions, conditions d'éclairage)

Ceci est particulièrement adapté à l'UMAP, car nous nous attendons à ce que les images d'une même personne soient regroupées, malgré les variations d'expression et d'éclairage.

Étape 1 : Importez les bibliothèques et chargez les données.

Tout d'abord, importons les bibliothèques nécessaires et chargeons notre ensemble de données :

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import matplotlib.cm as cm
from sklearn.datasets import fetch_olivetti_faces
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
import umap
import warnings
warnings.filterwarnings('ignore')

# Load the Olivetti faces dataset
faces = fetch_olivetti_faces(shuffle=True, random_state=42)
X = faces.data
y = faces.target

print(f"Dataset shape: {X.shape}")
print(f"Number of individuals: {len(np.unique(y))}")
print(f"Number of images per individual: {X.shape[0] // len(np.unique(y))}")

# Display sample faces
fig, axes = plt.subplots(2, 5, figsize=(12, 6))
for i, ax in enumerate(axes.flat):
   ax.imshow(X[i].reshape(64, 64), cmap='gray')
   ax.set_title(f'Person {y[i]}')
   ax.axis('off')
plt.suptitle('Sample Faces from the Dataset')
plt.tight_layout()
plt.show()

À partir du code ci-dessus, nous pouvons visualiser l'ensemble de données comme suit :

Étape 2 : Veuillez appliquer UMAP avec les paramètres par défaut.

L'ensemble de données Olivetti faces est pré-normalisé avec des valeurs de pixels comprises entre 0 et 1, ce qui nous permet d'appliquer directement l'UMAP :

# Create UMAP instance with default parameters
reducer = umap.UMAP(random_state=42)

# Fit and transform the data
embedding = reducer.fit_transform(X)

# Create a custom colormap for 40 distinct classes
colors = cm.get_cmap('hsv', 40)  

# Create visualization
plt.figure(figsize=(12, 10))
scatter = plt.scatter(embedding[:, 0], embedding[:, 1], c=y,
                    cmap=colors, s=50, alpha=0.8, edgecolors='black', linewidth=0.5)
plt.colorbar(scatter, label='Person ID', ticks=np.arange(0, 40, 5))
plt.title('UMAP Projection of Olivetti Faces (Default Parameters)')
plt.xlabel('UMAP 1')
plt.ylabel('UMAP 2')
plt.grid(True, alpha=0.3)
plt.show()

Nous observons un graphique coloré sous forme de visualisation UMAP :

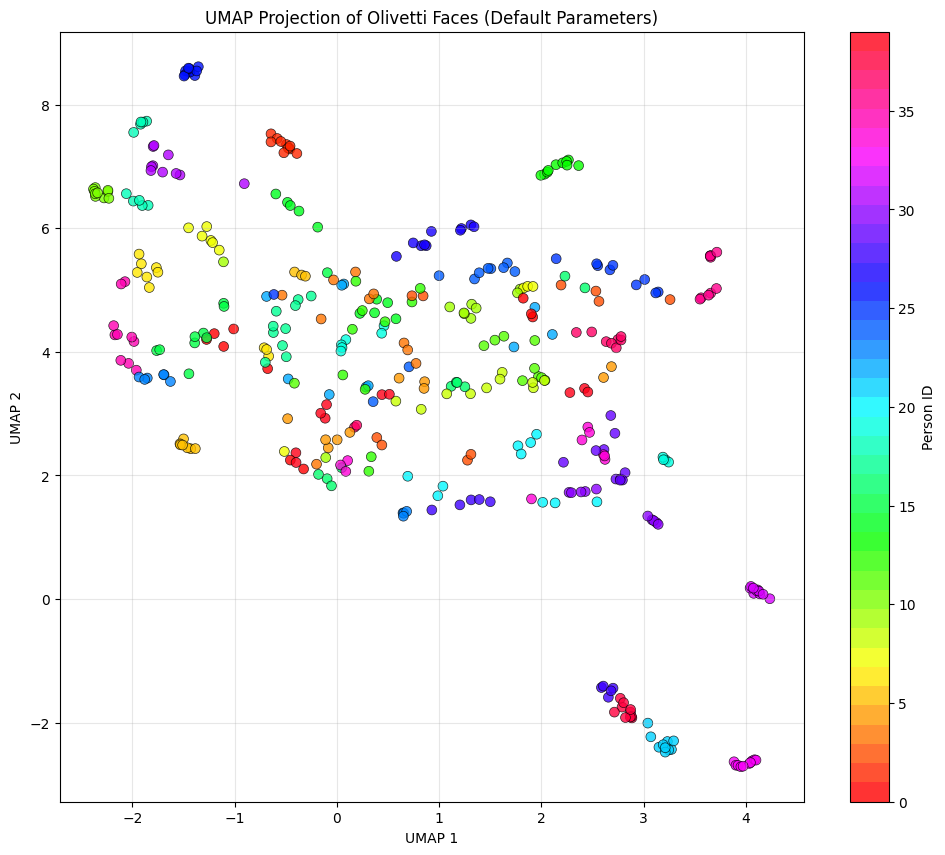
Voici quelques éléments à prendre en considération pour mieux comprendre le diagramme :

• Chaque point représente une image faciale.
• Les couleurs représentent différentes personnes (Identifiant de personne 0 à 39)
• La proximité implique la similitude : Les points proches les uns des autres représentent des visages que l'UMAP considère comme similaires dans l'espace à 4096 dimensions.

Bien que cela ne se produise pas dans la réalité, dans l'idéal, nous nous attendrions à ce que les 10 images d'une même personne (de même couleur) soient regroupées. Sur l'image, nous observons que certaines couleurs similaires sont regroupées lorsque nous avons créé l'UMAP à l'aide des paramètres par défaut.

Étape 3 : Découvrez les paramètres clés de l'UMAP

UMAP dispose de plusieurs paramètres importants qui contrôlent son fonctionnement. Examinons comment ils influencent les résultats :

# Create subplots for different parameter settings
fig, axes = plt.subplots(2, 3, figsize=(18, 12))
axes = axes.ravel()

# Different parameter configurations
param_configs = [
   {'n_neighbors': 5, 'min_dist': 0.1},
   {'n_neighbors': 15, 'min_dist': 0.1},
   {'n_neighbors': 50, 'min_dist': 0.1},
   {'n_neighbors': 15, 'min_dist': 0.0},
   {'n_neighbors': 15, 'min_dist': 0.5},
   {'n_neighbors': 15, 'min_dist': 0.99}
]

# Apply UMAP with different parameters
for idx, params in enumerate(param_configs):
   reducer = umap.UMAP(random_state=42, **params)
   embedding = reducer.fit_transform(X_scaled)
  
   ax = axes[idx]
   scatter = ax.scatter(embedding[:, 0], embedding[:, 1], c=y,
                       cmap='tab20', s=30, alpha=0.8)
   ax.set_title(f"n_neighbors={params['n_neighbors']}, "
                f"min_dist={params['min_dist']}")
   ax.set_xlabel('UMAP 1')
   ax.set_ylabel('UMAP 2')
   ax.grid(True, alpha=0.3)

plt.tight_layout()
plt.show()

La visualisation de la sortie est la suivante :

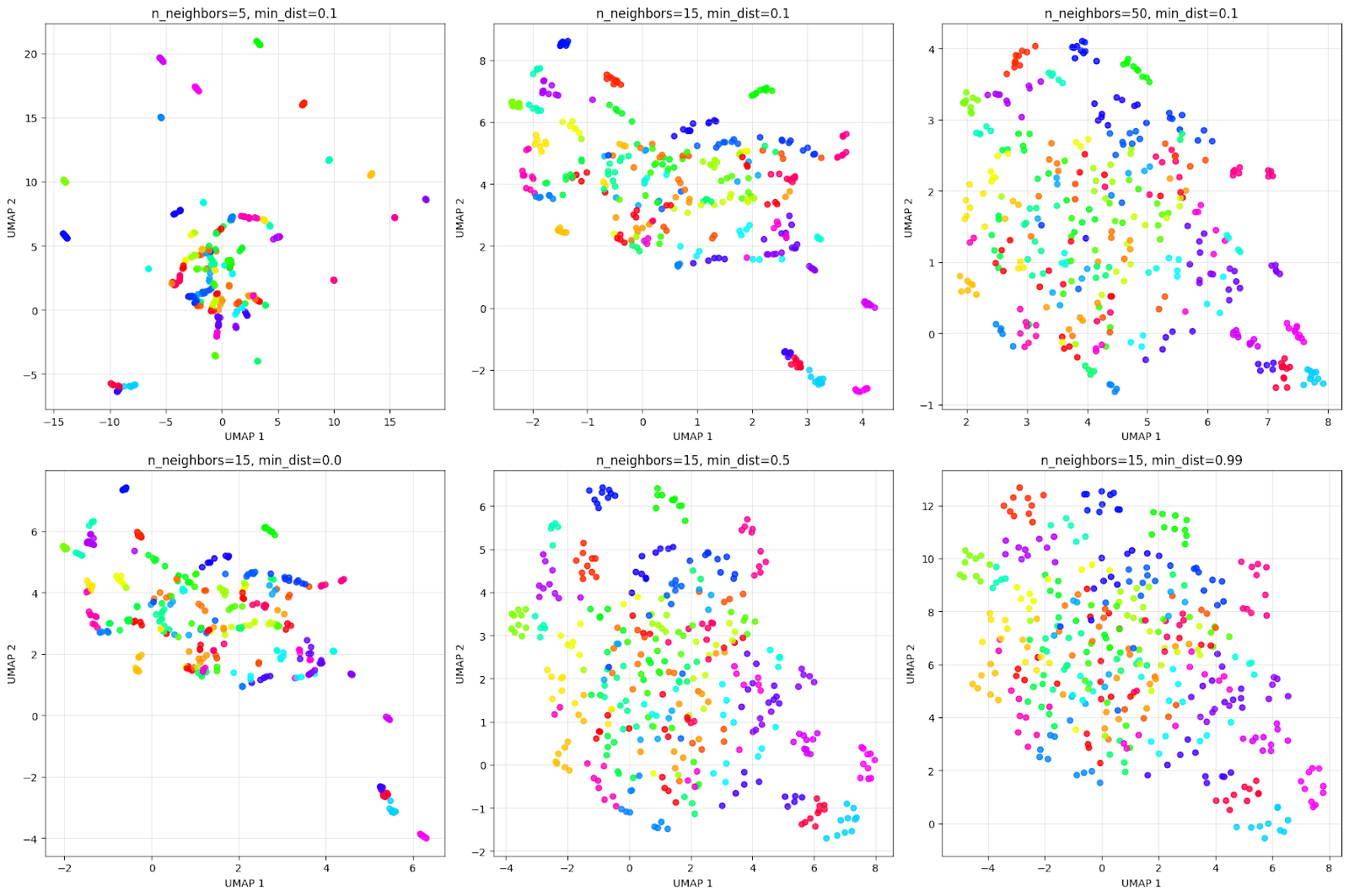
Le tableau ci-dessus illustre l'impact des paramètres sur la visualisation. En tenant compte de l'effet de la ligne supérieure de n_neighbors :

• n_voisins=5 : Vue très locale, crée de nombreux petits groupes compacts.
• n_voisins=15 : Une vision équilibrée, offrant un bon équilibre entre structure locale et structure mondiale.
• n_neighbors=50: Vue globale, elle se concentre sur la structure globale, en fusionnant éventuellement des individus similaires.

En considérant la ligne inférieure de l'effet min_dist :

• min_dist=0.0 : Les points sont extrêmement serrés, comme le montre la grille. Cela crée des grappes très serrées et denses.
• min_dist=0,5 : Espacement moyen entraînant des grappes plus dispersées.
• min_dist=0,99 : Un espacement maximal permet une répartition uniforme des points, mais entraîne une perte de la structure en grappes.

Il est toujours recommandé de tester ces paramètres afin d'obtenir le meilleur résultat de regroupement pour le problème en question.

Alternatives à l'UMAP pour la réduction de dimensionnalité

Poursuivons notre exemple avec l'ensemble de données Olivetti afin de comparer UMAP avec PCA et t-SNE et de comprendre leurs différences :

from sklearn.decomposition import PCA
from sklearn.manifold import TSNE

# Create figure with subplots
fig, axes = plt.subplots(1, 3, figsize=(18, 6))

colors = cm.get_cmap('hsv', 40)

# PCA
pca = PCA(n_components=2, random_state=42)
pca_result = pca.fit_transform(X)
axes[0].scatter(pca_result[:, 0], pca_result[:, 1], c=y,
               cmap=colors, s=50, alpha=0.8)
axes[0].set_title('PCA Projection')
axes[0].set_xlabel('PC 1')
axes[0].set_ylabel('PC 2')
axes[0].grid(True, alpha=0.3)

# t-SNE
tsne = TSNE(n_components=2, random_state=42, perplexity=30)
tsne_result = tsne.fit_transform(X)
axes[1].scatter(tsne_result[:, 0], tsne_result[:, 1], c=y,
               cmap=colors, s=50, alpha=0.8)
axes[1].set_title('t-SNE Projection')
axes[1].set_xlabel('t-SNE 1')
axes[1].set_ylabel('t-SNE 2')
axes[1].grid(True, alpha=0.3)

# UMAP
umap_reducer = umap.UMAP(n_neighbors=15, min_dist=0.1, random_state=42)
umap_result = umap_reducer.fit_transform(X)
scatter = axes[2].scatter(umap_result[:, 0], umap_result[:, 1], c=y,
                        cmap=colors, s=50, alpha=0.8)
axes[2].set_title('UMAP Projection')
axes[2].set_xlabel('UMAP 1')
axes[2].set_ylabel('UMAP 2')
axes[2].grid(True, alpha=0.3)

plt.tight_layout()
plt.show()

Nous observerons le graphique comparatif ci-dessous :

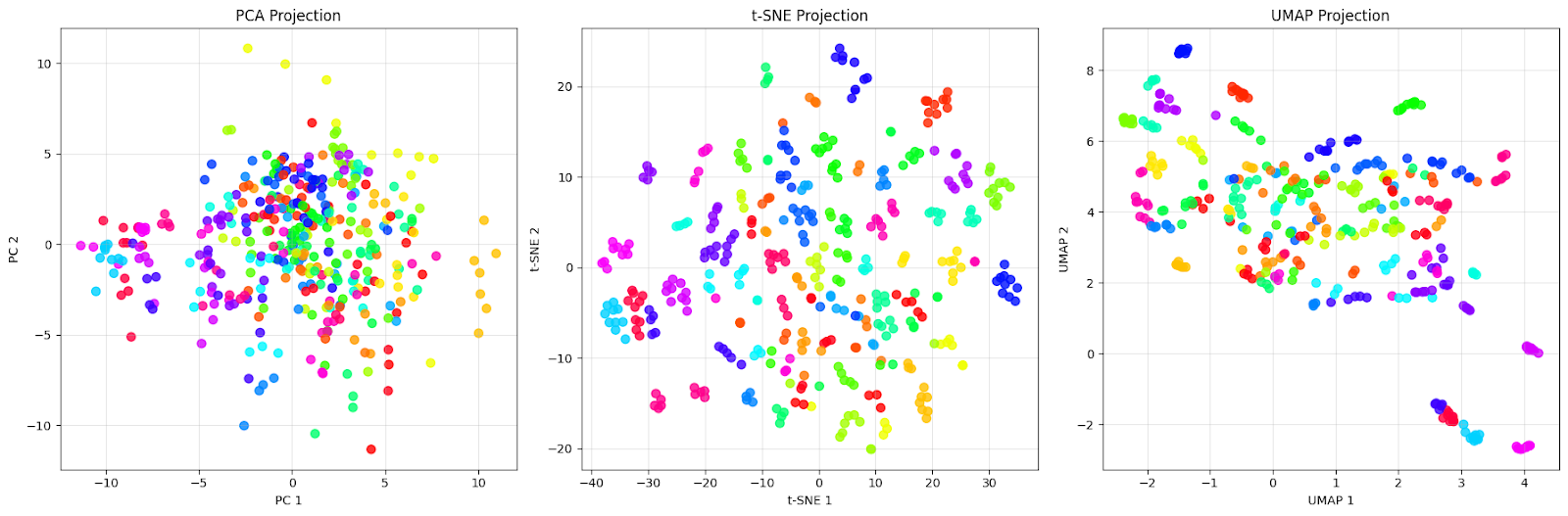
La projection PCA (à gauche) montre un cloud dense de points centrés autour de l'origine, avec un chevauchement important entre les points de différentes couleurs. C'est exactement ce que nous attendons de l'ACP : elle capture les directions de variance maximale dans les données, mais ne parvient pas à séparer efficacement les différentes personnes. Nous pouvons observer que les visages de différentes personnes (de différentes couleurs) sont complètement mélangés, rendant presque impossible l'identification de groupes distincts.

La projection t-SNE (au milieu) montre une amélioration avec des grappes bien séparées. Chaque couleur (représentant une personne différente) forme un groupe distinct et compact, avec des limites claires entre les différents individus. Veuillez noter comment t-SNE crée des regroupements locaux presque parfaits, où les visages d'une même personne sont rapprochés les uns des autres tout en étant éloignés des autres groupes. C'est là que réside la force du t-SNE : il excelle dans la préservation des voisinages locaux et la création de clusters visuellement distincts. 

La projection UMAP (à droite) adopte une approche différente. Bien que les grappes soient plus dispersées par rapport au t-SNE, cela reflète la volonté de l'UMAP de préserver à la fois la structure locale et globale. Nous pouvons observer que chaque individu forme toujours des groupes reconnaissables, mais avec davantage de variations internes. Certains groupes présentent un léger chevauchement ou sont positionnés plus près les uns des autres, ce qui pourrait indiquer des similitudes réelles entre ces individus.

Cette comparaison met en évidence un point important : la notion de « mieux » dépend de notre objectif. Si nous avons besoin d'une séparation visuelle aussi claire que possible pour la présentation ou l'exploration initiale, les clusters serrés de t-SNE sont excellents pour cet ensemble de données. Cependant, si nous souhaitons comprendre la structure globale des données et les relations entre les différents groupes, la préservation des relations globales par UMAP rend cette méthode plus appropriée pour cet ensemble de données.

Difficultés courantes rencontrées avec UMAP et solutions pour les surmonter

Comme pour tous les algorithmes et toutes les techniques, nous rencontrons plusieurs défis lorsque nous appliquons l'UMAP à des données réelles. 

Ayant beaucoup travaillé sur ce sujet, voici quelques défis récurrents que j'ai observés :

1. Choisir les paramètres appropriés

Le défi le plus courant consiste à sélectionner les valeurs appropriées pour n_neighbors et min_dist. Ces paramètres ont une incidence significative sur la visualisation, et il n'existe pas de solution universelle. 

Le paramètren_neighbors équilibre la préservation de la structure locale et globale. Les valeurs plus faibles (5-15) se concentrent sur la préservation des quartiers très locaux, capturant ainsi une structure très détaillée, mais risquant de fragmenter les schémas plus larges. Les valeurs plus élevées (30-100) mettent l'accent sur des modèles de connectivité plus larges, révélant la structure globale mais pouvant masquer les détails locaux. 

Le paramètremin_dist contrôle la densité des points dans la disposition à faible dimension, mais n'affecte pas la construction du graphe à haute dimension. Les valeurs proches de 0 permettent de regrouper les points de manière dense, créant ainsi des grappes visuellement compactes, tandis que les valeurs proches de 1 répartissent les points de manière plus uniforme dans l'espace de projection.

La meilleure approche consiste à commencer par les valeurs par défaut (n_neighbors=15, min_dist=0.1) et à les ajuster en fonction des caractéristiques de vos données :

• Pour les ensembles de données comportant des clusters clairs et bien séparés, nous pouvons utiliser des n_neighbors (5-15) afin de préserver la structure locale.
• Pour les ensembles de données présentant une structure plus continue ou hiérarchique, nous pouvons utiliser des n_neighbors (30-100) pour capturer les relations globales.
• Diminution min_dist (vers 0) pour un regroupement visuel plus serré dans la projection
• Augmentation de la min_dist (vers 0,5-1,0) pour obtenir des points plus uniformément répartis et plus faciles à distinguer visuellement.

2. Performances de calcul sur de grands ensembles de données

UMAP peut être lent sur des ensembles de données très volumineux (des millions de points), ce qui rend l'exploration interactive difficile. Nous pouvons mettre en pratique certaines des techniques ci-dessous afin d'améliorer les performances :

• Réduire le nombre d'époques pour une convergence plus rapide : umap.UMAP(n_epochs=200) (la valeur par défaut est None, qui sélectionne automatiquement en fonction de la taille de l'ensemble de données)
• Utilisation de l'initialisation aléatoire au lieu de l'initialisation spectrale pour les très grands ensembles de données : umap.UMAP(init='random')
• Sous-échantillonner nos données pour une exploration initiale, puis les appliquer à l'ensemble des données.
• En utilisant le n_jobs pour le traitement parallèle : umap.UMAP(n_jobs=-1)
• Paramétrage low_memory=False si nous disposons de suffisamment de RAM et souhaitons accélérer les calculs au détriment de l'utilisation de la mémoire.
• Utilisation de RAPIDS cuML pour l'accélération GPU sur du matériel compatible.
• Pour les ensembles de données volumineux, nous pouvons utiliser densmap=False (valeur par défaut), car la préservation DensMAP ajoute une charge de calcul supplémentaire.

3. Interprétation des distances dans les projections UMAP

Contrairement à l'ACP, les distances dans les projections UMAP n'ont pas d'interprétation directe. Les points qui semblent proches peuvent ne pas être similaires dans l'espace d'origine. Pour remédier à cette limitation, il est important de :

• Vérifiez les clusters trouvés dans UMAP en utilisant les caractéristiques originales.
• Utilisez principalement UMAP pour la visualisation et la génération d'hypothèses.
• Combiner UMAP avec d'autres techniques de validation, telles que les scores de silhouette.
• Conservez davantage de dimensions (3D ou 4D) pour les tâches d'analyse.

4. Problèmes de reproductibilité

UMAP utilise une initialisation aléatoire, ce qui peut entraîner des résultats différents d'une exécution à l'autre, rendant difficile la reproduction exacte des visualisations. Nous pouvons garantir la reproductibilité en suivant ces pratiques :

• Définir systématiquement le paramètre random_state: umap.UMAP(random_state=42)
• Pour les analyses critiques, il est recommandé d'exécuter UMAP à plusieurs reprises et de rechercher des modèles cohérents.
• Utilisation du paramètre init pour spécifier les positions initiales si une reproductibilité exacte est requise

5. Gestion des types de données mixtes

La mesure de distance par défaut de l'UMAP suppose des données numériques continues, ce qui peut poser problème pour les ensembles de données comportant des caractéristiques catégorielles ou mixtes. Lorsque nous travaillons avec des types de données mixtes, nous pouvons envisager les approches suivantes :

• Pré-traitement approprié des variables catégorielles (codage one-hot ou intégration)
• Utilisation de mesures de distance personnalisées qui gèrent des types de données mixtes
• Utilisation du paramètre metric avec des options telles que « hamming » pour les données binaires
• Appliquer UMAP séparément à différents types de caractéristiques, puis combiner les informations obtenues.

6. Valeurs aberrantes affectant la visualisation

Les valeurs aberrantes extrêmes peuvent comprimer la distribution principale des données, rendant difficile la visualisation de la structure dans la majorité des points. Voici quelques techniques que nous pouvons utiliser pour surmonter cette difficulté :

• Identification et suppression des valeurs aberrantes extrêmes avant l'application de l'UMAP
• Utilisation d'une mise à l'échelle robuste au lieu d'une mise à l'échelle standard
• Ajustement du paramètre d' local_connectivity e pour une meilleure résistance aux valeurs aberrantes
• Utilisation de la méthode de transformation UMAP pour projeter les valeurs aberrantes après ajustement sur des données propres

Bien que cette liste ne soit pas exhaustive, elle couvre les problèmes les plus courants rencontrés lors de l'utilisation d'UMAP. Comprendre ces problèmes et leurs solutions nous aidera à tirer le meilleur parti de l'UMAP.

Conclusion

Dans ce tutoriel, nous avons examiné le fonctionnement de l'UMAP tant sur le plan conceptuel que pratique, l'avons mis en œuvre sur des données réelles, l'avons comparé à d'autres méthodes et avons abordé les défis courants. Le point essentiel à retenir est que la capacité de l'UMAP à équilibrer la préservation des structures locales et globales le rend utile pour l'analyse exploratoire des données lorsqu'il s'agit de jeux de données complexes et de grande dimension.

Pour approfondir vos connaissances en matière de techniques de réduction de dimensionnalité, nous vous invitons à explorer notre cours sur la réduction de dimensionnalité en Python, où vous acquerrez une expérience pratique de l'UMAP ainsi que d'autres techniques telles que l'ACP et le t-SNE. Pour une perspective plus large sur la manière dont la réduction de dimensionnalité s'intègre dans les flux de travail du machine learning, le formation « Machine Learning Scientist with Python » vous enseigne les techniques d'apprentissage supervisé et non supervisé, vous aidant ainsi à élaborer des solutions complètes pour relever les défis liés aux données dans le monde réel.