Comprender UMAP: Guía completa sobre la reducción de dimensionalidad

A menudo nos encontramos con conjuntos de datos con cientos o incluso miles de características en problemas de machine learning, y esta escala suele plantear retos para la visualización y el análisis significativos de los datos. Los métodos tradicionales de gráficando solo pueden mostrar dos o tres dimensiones a la vez, lo que hace casi imposible comprender la estructura de los datos de alta dimensión. Aquí es donde las técnicas de reducción de dimensionalidad, como UMAP (aproximación y proyección uniformes de variedades), vienen al rescate.

Con el tiempo, UMAP se ha convertido en un método de referencia para visualizar conjuntos de datos complejos en diversos campos. Este tutorial te guiará a través de todo lo que necesitas saber sobre UMAP, desde sus fundamentos hasta su implementación práctica y los retos más comunes, ayudándote a empezar a utilizar esta técnica en tus proyectos a partir de ahora.

¿Qué es UMAP?

UMAP es un algoritmo de reducción de dimensionalidad no lineal que proyecta datos de alta dimensionalidad en un espacio de menor dimensionalidad (normalmente 2D o 3D) conservando la estructura esencial de los datos. UMAP son las siglas de Uniform Manifold Approximation and Projection (aproximación y proyección uniformes de variedades) y se basa en el aprendizaje de variedades y el análisis topológico de datos.

Otros métodos de reducción de dimensionalidad, como t-SNE, son buenos para preservar las vecindades locales, pero terminan distorsionando las relaciones globales. La ventaja principal de UMAP es que logra un equilibrio entre los barrios locales y las relaciones globales. Se supone que los datos se encuentran en una variedad riemanniana y que esta variedad puede modelarse localmente con una estructura topológica difusa. Esta base matemática permite a UMAP crear visualizaciones más significativas en las que los puntos de datos similares se agrupan manteniendo la topología general del conjunto de datos.

El algoritmo funciona construyendo una representación gráfica de alta dimensión de los datos y, a continuación, optimizando un gráfico de baja dimensión para que sea lo más similar posible en cuanto a estructura. Además de la visualización, UMAP resulta útil como paso previo al procesamiento para algoritmos de agrupamiento o incluso como técnica general de reducción de dimensionalidad no lineal para pipelines de machine learning.

Cómo funciona UMAP

Desglosaremos el proceso en varios pasos clave para comprender cómo funciona UMAP. La teoría matemática completa implica conceptos avanzados de topología y análisis de datos topológicos, por lo que en este tutorial adoptaremos un enfoque intuitivo del algoritmo central.

Paso 1: Construcción del gráfico de alta dimensión

UMAP comienza construyendo un gráfico ponderado que representa las relaciones en el espacio de alta dimensión. Para cada punto de datos, identifica sus k vecinos más cercanos (donde k es un parámetro que podemos ajustar). Sin embargo, a diferencia de los gráficos k-NN simples, UMAP utiliza un enfoque probabilístico. Calcula la probabilidad de que dos puntos estén conectados en función de su distancia, utilizando una aproximación suave que depende de la densidad local alrededor de cada punto.

La idea clave aquí es que UMAP se adapta a la estructura local de tus datos. En regiones densas, los puntos deben estar muy cerca para ser considerados vecinos, mientras que en regiones dispersas, el algoritmo amplía su radio de búsqueda. 

Este comportamiento adaptativo se controla mediante la fórmula:

p(i,j) = exp(-(d(xi, xj) - ρi) / σi)

Donde d(xi, xj) es la distancia entre puntos, ρi es la distancia al vecino más cercano y σi es un factor de escala calculado para cada punto.

Paso 2: Creación de una representación topológica difusa

A continuación, UMAP convierte estas distribuciones de probabilidad locales en una estructura topológica difusa a partir del análisis de datos topológicos. Simetriza el gráfico combinando las probabilidades de ambas direcciones:

p(i,j) = p(i|j) + p(j|i) - p(i|j) * p(j|i)

Esto crea lo que se denomina un conjunto simplicial difuso, que captura la estructura múltiple de los datos de alta dimensión.

Paso 3: Optimización de la representación de baja dimensión

El último paso consiste en encontrar una representación de baja dimensión que conserve la estructura topológica difusa. UMAP inicializa puntos en el espacio de baja dimensión (utilizando una incrustación espectral) y, a continuación, utiliza el descenso de gradiente para minimizar la entropía cruzada entre las representaciones topológicas difusas de alta y baja dimensión.

La optimización utiliza fuerzas de atracción para unir puntos que deberían estar cerca (basándose en la estructura de alta dimensión) y fuerzas de repulsión para separar puntos que deberían estar distantes. Esta dinámica de empuje y tracción crea las visualizaciones características en las que los clústeres están bien separados, al tiempo que mantienen su estructura interna.

Aplicaciones prácticas de UMAP

UMAP tiene aplicaciones en numerosos campos en los que resulta útil comprender los datos de alta dimensión. 

Algunas de estas aplicaciones en el mundo real incluyen:

• Genómica unicelular y bioinformática: En la investigación genómica, UMAP se ha convertido en el estándar para visualizar datos de secuenciación de ARN unicelular. Los investigadores lo utilizan para identificar tipos de células, rastrear trayectorias de desarrollo y comprender la progresión de las enfermedades. Al reducir miles de mediciones de expresión génica a un gráfico bidimensional, UMAP revela distintas poblaciones celulares y sus relaciones, algo que sería imposible de apreciar en los datos sin procesar.
• Procesamiento del lenguaje natural: Los datos de texto, cuando se convierten en incrustaciones de alta dimensión, pueden visualizarse utilizando UMAP para comprender las relaciones semánticas. Se utiliza habitualmente para visualizar incrustaciones de palabras, grupos de documentos y depurar modelos lingüísticos, mostrando cómo se relacionan entre sí diferentes conceptos en el espacio de incrustación.
• Visión artificial y análisis de imágenes: UMAP ayuda a visualizar las representaciones de características aprendidas por las redes neuronales, lo que facilita la comprensión de los patrones que ha aprendido el modelo. También se utiliza en sistemas de reconocimiento facial para visualizar cómo se agrupan los rostros en función de sus características, y en imágenes médicas para identificar casos similares o anomalías.
• Exploración de datos y detección de valores atípicos: UMAP ayuda a revelar patrones ocultos y a detectar valores atípicos en conjuntos de datos complejos proyectándolos en un espacio visual interpretable. Este enfoque visual para la detección de valores atípicos resulta especialmente valioso cuando los métodos estadísticos tradicionales tienen dificultades con las interacciones de alta dimensión.
• Segmentación de clientes y análisis de mercado: Los equipos de marketing utilizan UMAP para visualizar los patrones de comportamiento de los clientes basándose en múltiples características, como el historial de compras, los datos demográficos y las métricas de interacción. Esto ayuda a identificar segmentos de clientes diferenciados y a comprender las relaciones entre los distintos grupos.
• Descubrimiento de fármacos: Los investigadores farmacéuticos utilizan UMAP para visualizar espacios de compuestos químicos, lo que les ayuda a identificar candidatos prometedores para fármacos al ver qué compuestos se agrupan cerca de fármacos eficaces conocidos y se alejan de compuestos tóxicos.

Ahora que hemos comprendido el concepto, los fundamentos matemáticos y las aplicaciones prácticas de UMAP, pasemos a la implementación.

Implementación de UMAP en Python

Implementemos UMAP en un conjunto de datos del mundo real para ver cómo funciona en la práctica. Utilizaremos el conjunto de datos Olivetti Faces, que contiene imágenes en escala de grises de rostros de 40 personas diferentes. El conjunto de datos Olivetti se puede descargar desde Kaggle o a través de la biblioteca Python scikit-learn.

El conjunto de datos Olivetti Faces contiene:

• 400 imágenes en escala de grises (64 x 64 píxeles = 4096 dimensiones)
• 40 personas diferentes
• 10 imágenes por persona (diferentes expresiones, condiciones de iluminación)

Esto es perfecto para UMAP, ya que esperamos que las imágenes de la misma persona se agrupen, a pesar de las variaciones en la expresión y la iluminación.

Paso 1: Importar bibliotecas y cargar los datos

En primer lugar, importemos las bibliotecas necesarias y carguemos nuestro conjunto de datos:

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import matplotlib.cm as cm
from sklearn.datasets import fetch_olivetti_faces
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
import umap
import warnings
warnings.filterwarnings('ignore')

# Load the Olivetti faces dataset
faces = fetch_olivetti_faces(shuffle=True, random_state=42)
X = faces.data
y = faces.target

print(f"Dataset shape: {X.shape}")
print(f"Number of individuals: {len(np.unique(y))}")
print(f"Number of images per individual: {X.shape[0] // len(np.unique(y))}")

# Display sample faces
fig, axes = plt.subplots(2, 5, figsize=(12, 6))
for i, ax in enumerate(axes.flat):
   ax.imshow(X[i].reshape(64, 64), cmap='gray')
   ax.set_title(f'Person {y[i]}')
   ax.axis('off')
plt.suptitle('Sample Faces from the Dataset')
plt.tight_layout()
plt.show()

A partir del código anterior, podemos visualizar el conjunto de datos de la siguiente manera:

Paso 2: Aplica UMAP con los parámetros predeterminados.

El conjunto de datos Olivetti Faces viene pre-normalizado con valores de píxeles entre 0 y 1, por lo que podemos aplicar UMAP directamente:

# Create UMAP instance with default parameters
reducer = umap.UMAP(random_state=42)

# Fit and transform the data
embedding = reducer.fit_transform(X)

# Create a custom colormap for 40 distinct classes
colors = cm.get_cmap('hsv', 40)  

# Create visualization
plt.figure(figsize=(12, 10))
scatter = plt.scatter(embedding[:, 0], embedding[:, 1], c=y,
                    cmap=colors, s=50, alpha=0.8, edgecolors='black', linewidth=0.5)
plt.colorbar(scatter, label='Person ID', ticks=np.arange(0, 40, 5))
plt.title('UMAP Projection of Olivetti Faces (Default Parameters)')
plt.xlabel('UMAP 1')
plt.ylabel('UMAP 2')
plt.grid(True, alpha=0.3)
plt.show()

Se nos presenta un gráfico de dispersión en color como visualización UMAP:

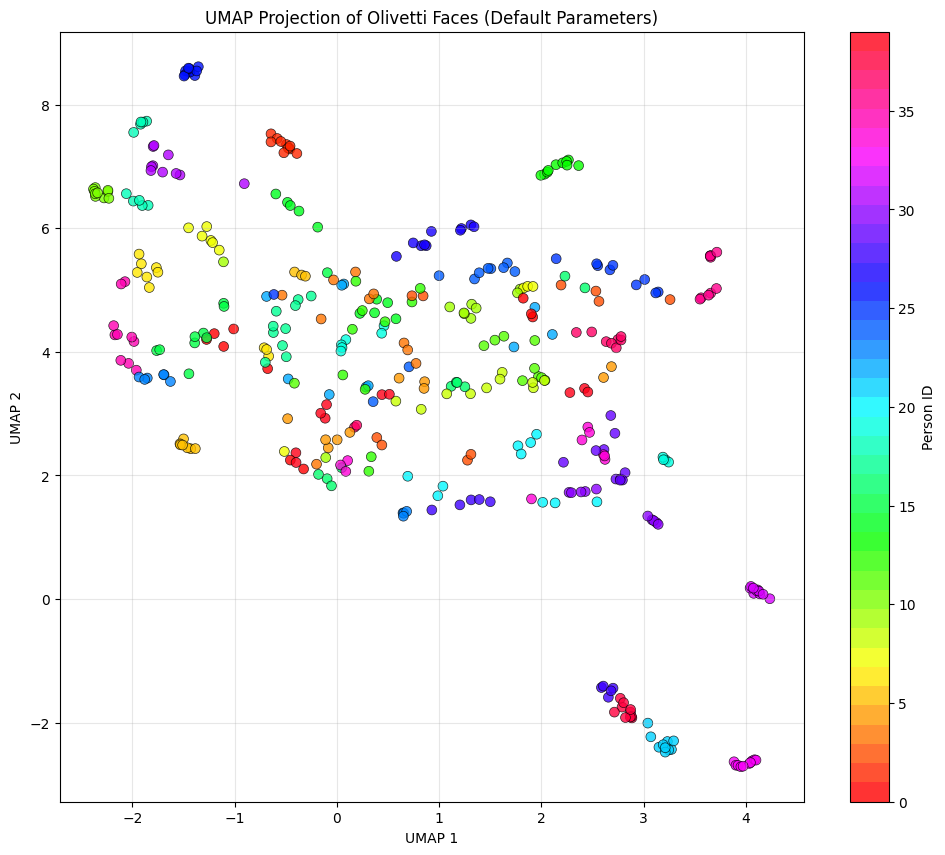
Aquí hay algunas cosas que debes tener en cuenta para comprender mejor el diagrama:

• Cada punto representa una imagen facial.
• Los colores representan a diferentes personas (ID de persona 0-39).
• La proximidad implica similitud: Los puntos cercanos entre sí son caras que UMAP considera similares en el espacio de 4096 dimensiones.

Aunque no ocurre en situaciones reales, lo ideal sería que las 10 imágenes de la misma persona (del mismo color) se agruparan juntas. En la imagen, vemos algunos de los colores similares agrupados cuando creamos el UMAP utilizando los parámetros predeterminados.

Paso 3: Explora los parámetros clave de UMAP

UMAP tiene varios parámetros importantes que controlan su comportamiento. Veamos cómo afectan a los resultados:

# Create subplots for different parameter settings
fig, axes = plt.subplots(2, 3, figsize=(18, 12))
axes = axes.ravel()

# Different parameter configurations
param_configs = [
   {'n_neighbors': 5, 'min_dist': 0.1},
   {'n_neighbors': 15, 'min_dist': 0.1},
   {'n_neighbors': 50, 'min_dist': 0.1},
   {'n_neighbors': 15, 'min_dist': 0.0},
   {'n_neighbors': 15, 'min_dist': 0.5},
   {'n_neighbors': 15, 'min_dist': 0.99}
]

# Apply UMAP with different parameters
for idx, params in enumerate(param_configs):
   reducer = umap.UMAP(random_state=42, **params)
   embedding = reducer.fit_transform(X_scaled)
  
   ax = axes[idx]
   scatter = ax.scatter(embedding[:, 0], embedding[:, 1], c=y,
                       cmap='tab20', s=30, alpha=0.8)
   ax.set_title(f"n_neighbors={params['n_neighbors']}, "
                f"min_dist={params['min_dist']}")
   ax.set_xlabel('UMAP 1')
   ax.set_ylabel('UMAP 2')
   ax.grid(True, alpha=0.3)

plt.tight_layout()
plt.show()

La visualización de la salida es la siguiente:

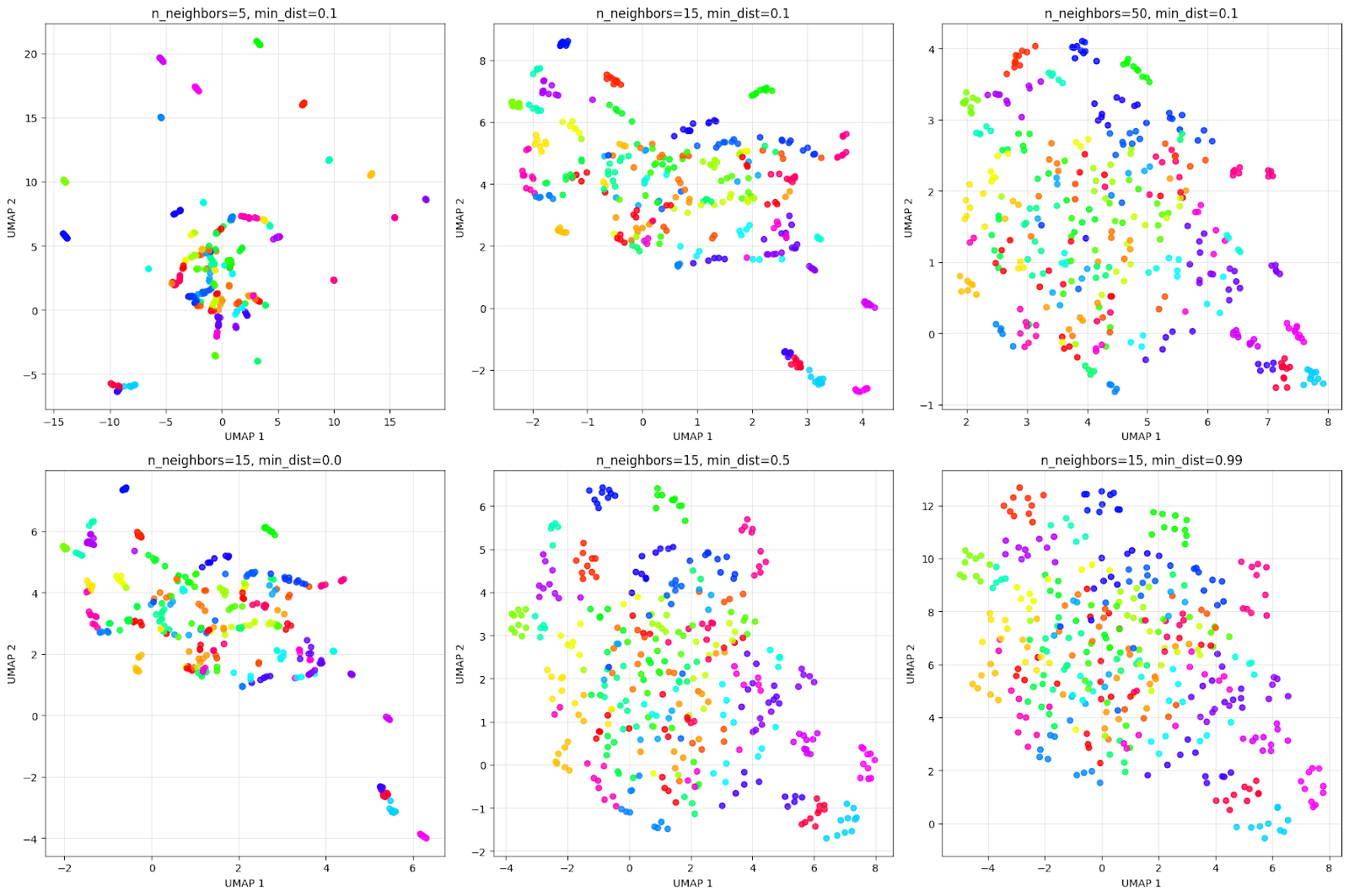
La parilla anterior ilustra cómo los parámetros afectan a la visualización. Teniendo en cuenta el efecto de la fila superior de n_neighbors:

• n_neighbors=5: Vista muy local, crea muchos grupos pequeños y compactos.
• n_neighbors=15: Visión equilibrada, ofrece una buena combinación de estructura local y global.
• n_neighbors=50: Visión global: se centra en la estructura general, fusionando potencialmente a individuos similares.

Teniendo en cuenta la fila inferior del efecto min_dist:

• min_dist=0.0: Los puntos están muy igualados, como se puede ver en la parilla. Esto crea racimos muy compactos y densos.
• min_dist=0.5: El espaciamiento medio da lugar a racimos más dispersos.
• min_dist=0.99: El espaciado máximo da como resultado una distribución uniforme de los puntos, pero pierde la estructura de agrupamiento.

Siempre es recomendable experimentar con estos parámetros para obtener el mejor resultado de agrupamiento para el problema en cuestión.

Alternativas a UMAP para la reducción de dimensionalidad

Continuemos con nuestro ejemplo con el conjunto de datos Olivetti para comparar UMAP con PCA y t-SNE y comprender sus diferencias:

from sklearn.decomposition import PCA
from sklearn.manifold import TSNE

# Create figure with subplots
fig, axes = plt.subplots(1, 3, figsize=(18, 6))

colors = cm.get_cmap('hsv', 40)

# PCA
pca = PCA(n_components=2, random_state=42)
pca_result = pca.fit_transform(X)
axes[0].scatter(pca_result[:, 0], pca_result[:, 1], c=y,
               cmap=colors, s=50, alpha=0.8)
axes[0].set_title('PCA Projection')
axes[0].set_xlabel('PC 1')
axes[0].set_ylabel('PC 2')
axes[0].grid(True, alpha=0.3)

# t-SNE
tsne = TSNE(n_components=2, random_state=42, perplexity=30)
tsne_result = tsne.fit_transform(X)
axes[1].scatter(tsne_result[:, 0], tsne_result[:, 1], c=y,
               cmap=colors, s=50, alpha=0.8)
axes[1].set_title('t-SNE Projection')
axes[1].set_xlabel('t-SNE 1')
axes[1].set_ylabel('t-SNE 2')
axes[1].grid(True, alpha=0.3)

# UMAP
umap_reducer = umap.UMAP(n_neighbors=15, min_dist=0.1, random_state=42)
umap_result = umap_reducer.fit_transform(X)
scatter = axes[2].scatter(umap_result[:, 0], umap_result[:, 1], c=y,
                        cmap=colors, s=50, alpha=0.8)
axes[2].set_title('UMAP Projection')
axes[2].set_xlabel('UMAP 1')
axes[2].set_ylabel('UMAP 2')
axes[2].grid(True, alpha=0.3)

plt.tight_layout()
plt.show()

Veremos el gráfico comparativo a continuación:

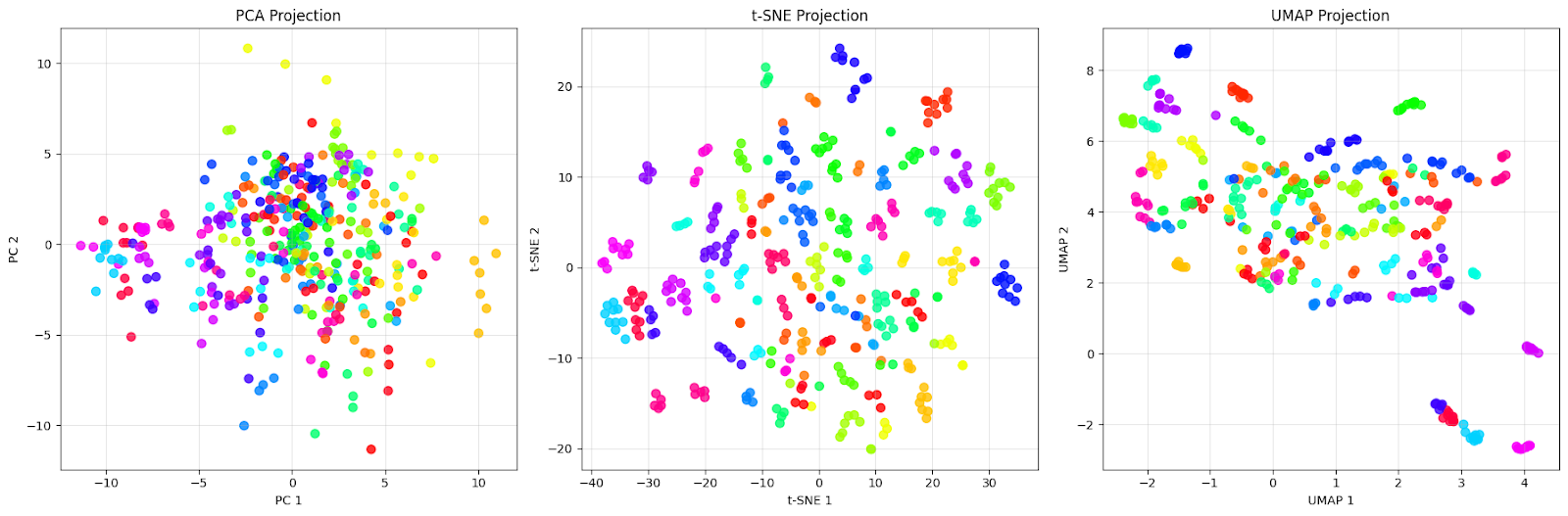
La proyección PCA (izquierda) muestra una densa nube de puntos centrados alrededor del origen con un amplio solapamiento entre los puntos de diferentes colores. Esto es exactamente lo que esperamos del PCA: captura las direcciones de máxima varianza en los datos, pero no logra separar eficazmente a las diferentes personas. Podemos ver que los rostros de diferentes individuos (diferentes colores) están completamente mezclados, lo que hace casi imposible identificar grupos distintos.

La proyección t-SNE (en el centro) muestra una mejora con grupos bien separados. Cada color (que representa a una persona diferente) forma un grupo distinto y compacto, con límites claros entre los distintos individuos. Observa cómo t-SNE crea agrupaciones locales casi perfectas en las que los rostros de una misma persona se agrupan muy cerca entre sí, al tiempo que se alejan de otros grupos. Esta es la ventaja de t-SNE: destaca por preservar los vecindarios locales y crear grupos visualmente diferenciados. 

La proyección UMAP (derecha) adopta un enfoque diferente. Aunque los clústeres están más dispersos en comparación con t-SNE, esto refleja el intento de UMAP de preservar tanto la estructura local como la global. Podemos ver que cada persona sigue formando grupos reconocibles, pero con más variación interna. Algunos grupos muestran un ligero solapamiento o están situados más cerca unos de otros, lo que podría indicar similitudes reales entre esos individuos.

Esta comparación ilustra un punto importante: «mejor» depende de nuestro objetivo. Si necesitamos la separación visual más clara posible para la presentación o la exploración inicial, los clústeres compactos de t-SNE son excelentes para este conjunto de datos. Sin embargo, si queremos comprender la estructura general de los datos y cómo se relacionan entre sí los diferentes grupos, la preservación de las relaciones globales que ofrece UMAP lo hace más adecuado para este conjunto de datos.

Problemas comunes con UMAP y cómo resolverlos

Al igual que con todos los algoritmos y técnicas, te enfrentas a varios retos al aplicar UMAP a datos del mundo real. 

Después de haber trabajado mucho en esto, estas son algunas de las dificultades que he observado y que se repiten constantemente:

1. Elegir los parámetros adecuados

El reto más habitual es seleccionar los valores adecuados para n_neighbors y min_dist. Estos parámetros afectan significativamente a la visualización, y no existe una solución única que se adapte a todos los casos. 

El parámetron_neighbors equilibra la preservación de la estructura local frente a la global. Los valores más pequeños (5-15) se centran en preservar barrios muy locales, capturando una estructura muy detallada, pero con el riesgo de fragmentar patrones más amplios. Los valores más altos (30-100) enfatizan patrones de conectividad más amplios, revelando la estructura global, pero ocultando potencialmente los detalles locales. 

El parámetromin_dist controla la densidad con la que se agrupan los puntos en el diseño de baja dimensión, pero no afecta a la construcción del gráfico de alta dimensión. Los valores cercanos a 0 permiten agrupar los puntos de forma densa, creando agrupaciones visualmente compactas, mientras que los valores cercanos a 1 distribuyen los puntos de forma más uniforme por el espacio de proyección.

El mejor enfoque es comenzar con los valores predeterminados (n_neighbors=15, min_dist=0.1) y ajustarlos en función de las características de tus datos:

• Para conjuntos de datos con clústeres claros y bien separados, podemos utilizar un número menor de n_neighbors (5-15) para conservar la estructura local.
• Para conjuntos de datos con una estructura más continua o jerárquica, podemos utilizar n_neighbors (30-100) para capturar relaciones globales.
• Disminución min_dist (hacia 0) para obtener una agrupación visual más precisa en la proyección.
• Aumentar min_dist (hacia 0,5-1,0) para obtener puntos distribuidos de manera más uniforme y más fáciles de distinguir visualmente.

2. Rendimiento computacional en grandes conjuntos de datos

UMAP puede ser lento con conjuntos de datos muy grandes (millones de puntos), lo que dificulta la exploración interactiva. Podemos probar algunas de las siguientes técnicas para mejorar el rendimiento:

• Reducir el número de épocas para una convergencia más rápida: umap.UMAP(n_epochs=200) (el valor predeterminado es None, que se selecciona automáticamente en función del tamaño del conjunto de datos).
• Uso de inicialización aleatoria en lugar de espectral para conjuntos de datos muy grandes: umap.UMAP(init='random')
• Submuestreo de nuestros datos para la exploración inicial y posterior aplicación al conjunto de datos completo.
• Usando el n_jobs para el procesamiento paralelo: umap.UMAP(n_jobs=-1)
• Configuración low_memory=False si tienes suficiente RAM y deseas un cálculo más rápido a costa del uso de memoria.
• Uso de RAPIDS cuML para la aceleración de GPU en hardware compatible.
• Para conjuntos de datos grandes, podemos usar densmap=False (el valor predeterminado), ya que la preservación DensMAP añade una sobrecarga computacional.

3. Interpretación de distancias en proyecciones UMAP

A diferencia del PCA, las distancias en las proyecciones UMAP no tienen una interpretación directa. Los puntos que parecen cercanos pueden no ser similares en el espacio original. Para abordar esta limitación, es importante:

• Valida los clústeres encontrados en UMAP utilizando las características originales.
• Utiliza UMAP principalmente para la visualización y la generación de hipótesis.
• Combina UMAP con otras técnicas de validación, como las puntuaciones de silueta.
• Conserva más dimensiones (3D o 4D) para las tareas de análisis.

4. Problemas de reproducibilidad

UMAP utiliza una inicialización aleatoria, lo que puede dar lugar a resultados diferentes entre ejecuciones, lo que dificulta la reproducción de visualizaciones exactas. Podemos garantizar la reproducibilidad siguiendo estas prácticas:

• Siempre se establece el parámetro random_state: umap.UMAP(random_state=42)
• Para realizar análisis críticos, ejecuta UMAP varias veces y busca patrones consistentes.
• Uso del parámetro init para especificar posiciones iniciales si se requiere una reproducibilidad exacta.

5. Manejo de tipos de datos mixtos

La métrica de distancia predeterminada de UMAP asume datos numéricos continuos, lo que puede ser problemático para conjuntos de datos con características categóricas o mixtas. Cuando trabajamos con tipos de datos mixtos, podemos considerar estos enfoques:

• Preprocesamiento adecuado de variables categóricas (codificación one-hot o incrustación)
• Uso de métricas de distancia personalizadas que manejan tipos de datos mixtos
• Uso del parámetro metric con opciones como «hamming» para datos binarios.
• Aplicar UMAP por separado a diferentes tipos de características y luego combinar los resultados.

6. Valores atípicos que distorsionan la visualización

Los valores atípicos extremos pueden comprimir la distribución principal de los datos, lo que dificulta ver la estructura en la mayoría de los puntos. Algunas técnicas que podemos utilizar para superar esto son:

• Identificar y eliminar valores atípicos extremos antes de aplicar UMAP.
• Usar escalado robusto en lugar de escalado estándar
• Ajustar el parámetro « local_connectivity » para que sea más robusto ante valores atípicos.
• Uso del método de transformación UMAP para proyectar valores atípicos tras ajustarlos a datos limpios.

Aunque esta lista no es exhaustiva, cubre los problemas más comunes a los que te enfrentas al trabajar con UMAP. Comprender estos problemas y sus soluciones nos ayudará a sacar el máximo partido a UMAP.

Conclusión

A través de este tutorial, hemos explorado cómo funciona UMAP tanto a nivel conceptual como práctico, lo hemos implementado en datos reales, lo hemos comparado con métodos alternativos y hemos abordado retos comunes. La conclusión principal es que la capacidad de UMAP para equilibrar la preservación de la estructura local y global lo hace útil para el análisis exploratorio de datos cuando se trata de conjuntos de datos complejos y de alta dimensión.

Para profundizar tus conocimientos sobre las técnicas de reducción de dimensionalidad, te recomendamos que explores nuestro Reducción de dimensionalidad en Python, donde obtendrás experiencia práctica con UMAP junto con otras técnicas como PCA y t-SNE. Para obtener una perspectiva más amplia sobre cómo encaja la reducción de dimensionalidad en los flujos de trabajo de machine learning, el Curso de científico de machine learning con Python te enseña técnicas de aprendizaje supervisado y no supervisado, lo que te ayudará a crear soluciones integrales para los retos que plantean los datos del mundo real.