Kurs
Die Glockenkurve, die viele Namen hat, wie z.B. die Normalverteilung oder die Gauß-Verteilung, wird dir praktisch überall auffallen, vor allem, wenn du dich mit Statistik oder Datenwissenschaft beschäftigst. Es fühlt sich an, ist aber kein Zufall der Natur: Es stellt sich heraus, dass vieles von dem, was wir messen, das Ergebnis vieler kleiner Faktoren ist, die sich addieren, was auf ein zugrunde liegendes additives Modell hindeutet. Das zentrale Grenzwertsatztheorem erklärt warum: Wenn eine Variable von vielen kleinen, unabhängigen Faktoren beeinflusst wird, neigt die Summe dieser Variablen dazu, einer Normalverteilung zu folgen, unabhängig davon, aus welchen Verteilungen sie ursprünglich stammen.
Durch die Umwandlung jeder Normalverteilung in eine spezielle Form, die sogenannte Standardnormalverteilung, können wir das Vorhandensein dieses additiven Modells nutzen und einen Schritt weiter gehen, indem wir diese Verteilung standardisieren, um sie in bestimmten Kontexten noch nützlicher zu machen. Wir werden erkunden, wie die Standardnormalverteilung verwendet wird, um Wahrscheinlichkeiten zu berechnen, statistische Schlüsse zu ziehen und statistische Tests mit Hilfe bekannter Eigenschaften der Verteilung anzuwenden. Am Ende dieses Artikels wirst du wissen, was die Standardnormalverteilung ist, warum wir sie standardisieren und wie das alles mit Variabilität, Wahrscheinlichkeit und Hypothesentests zusammenhängt. Ich hoffe, dass du dich am Ende auch für unseren Kurs "Einführung in die Statistik in R" oder unseren Lernpfad " Statistische Schlussfolgerungen in R " einträgst, um die Ideen in diesem Artikel weiter auszubauen.
Was ist die Standard-Normalverteilung?
Die Standardnormalverteilung ist eine besondere Form der Normalverteilung, bei der der Mittelwert gleich Null und die Standardabweichung gleich Eins ist. Wir sollten auch sagen, dass die Verteilung symmetrisch ist und dass die Wahrscheinlichkeiten für bestimmte Werte symmetrisch abnehmen, je weiter du dich vom Zentrum entfernst.

"Standard Normal Distribution" Bild von Dall-E
Die Gleichungen der Standard-Normalverteilung verstehen
Schauen wir uns die mathematischen Aspekte der Standard-Normalverteilung etwas genauer an.
Die PDF der Standard-Normalverteilung
Wenn du mit dem Begriff der Wahrscheinlichkeitsdichtefunktion (PDF) nicht vertraut bist, solltest du wissen, dass sie beschreibt, wie die Wahrscheinlichkeiten über die möglichen Werte einer kontinuierlichen Zufallsvariablen verteilt sind. Jede kontinuierliche Wahrscheinlichkeitsverteilung, wie die Exponentialverteilung, die t-Verteilung oder die Cauchy-Verteilung, hat ihre eigene Wahrscheinlichkeitsdichtefunktion, die die Kurve definiert. Die PDF der Standardnormalverteilung wird hier definiert: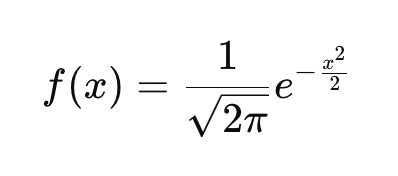
Diese Funktion sorgt dafür, dass die Fläche unter der Kurve zu 1 integriert wird. Wenn du dir die Gleichung ansiehst und verschiedene Werte von x einsetzt, erhältst du die Höhe der Kurve an diesen Punkten. In der Gleichung:
- x steht für eine beliebige reelle Zahl und ist die Eingangsvariable für die Funktion. Er erscheint im Exponenten der Funktion, der -x2/2 ist. Damit wird die Form der Kurve gesteuert.
- Da x2 immer nicht negativ ist und ein negatives Vorzeichen vorangestellt ist, ist der Exponent immer negativ oder Null.
- In dem speziellen Fall, in dem x=0 ist, ist der Exponent am größten, sodass f(x) seinen Höchstwert erreicht.
- Wenn sich x entweder in positiver oder negativer Richtung von 0 wegbewegt, erhöht sich x2, wodurch der Exponent negativer wird. Ein negativerer Exponent führt zu einem kleineren Funktionswert, was zusammen mit den anderen Dingen, die wir gesagt haben, bedeutet, dass f(x) auf beiden Seiten von x=0 symmetrisch abnimmt.
- Die Basis des Exponenten, die Eulersche Zahl, sorgt dafür, dass die Funktion schnell abfällt, wenn sich x in beide Richtungen weiter von Null entfernt.
- Die Konstante 1/√(2π) sorgt dafür, dass die Gesamtfläche unter der Kurve gleich 1 ist.
Die CDF der Standardnormalverteilung
Im Gegensatz zur PDF, die die relative Wahrscheinlichkeit verschiedener Werte angibt, sagt die CDF aus, wie hoch die Wahrscheinlichkeit ist, dass eine Variable kleiner oder gleich einem bestimmten Wert ist. Genau wie die PDF hat auch jede kontinuierliche Wahrscheinlichkeitsverteilung ihre eigene CDF.
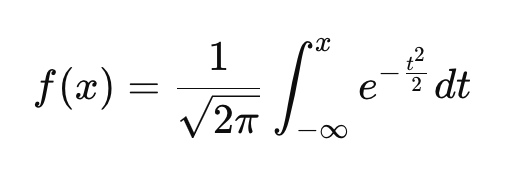
Diese Gleichung ist ein bisschen komplizierter, aber wir können sie durcharbeiten:
- Das Integral bedeutet, dass die CDF nicht die Höhe der Kurve bei x angibt, sondern die Gesamtwahrscheinlichkeit von -∞ bis x.
- Wenn x→-∞, nähert sich die CDF dem Wert 0.
- Wenn x=0 ist die CDF 0,5, da die Verteilung symmetrisch ist und die Hälfte der Wahrscheinlichkeit links von Null liegt.
- Als x→∞nähert sich die CDF dem Wert 1.
Warum wir uns für die Standard-Normalverteilung interessieren
In unserem Leitfaden zur Gauß-Verteilung findest du einige gute Ideen, wann du deine Daten an eine Normalverteilung anpassen solltest. Aber manchmal möchtest du deine Daten vielleicht speziell in eine Standardnormale umwandeln. Hier sind einige häufige Gründe dafür:
Die Standardnormale wird bei Hypothesentests verwendet
Eine Standard-Normalverteilung macht unsere Daten besser vergleichbar und mit bestimmten statistischen Methoden nutzbar. Indem wir Daten in Z-Werte umwandeln, können wir Beobachtungen mit verschiedenen Normalverteilungen vergleichen. Sie bildet insbesondere die Grundlage für Z-Tests, die wir verwenden, wenn wir feststellen wollen, ob sich ein Stichprobenmittelwert signifikant von einem Populationsmittelwert unterscheidet.
Der t-Test hingegen verwendet die Standardabweichung der Stichprobe als Schätzung der Standardabweichung der Grundgesamtheit, weshalb er sich auf die t-Verteilung stützt, die schwerere Schwänze hat als die Standardnormalverteilung. Lies unser Tutorium T-Test vs. Z-test: When to Use Each, in dem es um Dinge wie Populations- und Stichprobenvarianz geht.
Die Standardnormale vergleicht Daten auf einer gemeinsamen Skala
Da verschiedene Datensätze und Variablen unterschiedliche Einheiten und Maßstäbe haben können, können direkte Vergleiche schwierig sein. Aber wenn du sie in Z-Werte umwandelst, indem du den Mittelwert abziehst und durch die Standardabweichung teilst, kannst du verschiedene Verteilungen leicht miteinander vergleichen. Bei Anwendung auf einen normalverteilten Datensatz ergibt dies eine Standardnormalverteilung. Wenn wir zum Beispiel die SAT- und GRE-Ergebnisse, von denen ich annehme, dass sie normalverteilt sind, in Z-Werte umwandeln, können wir die Leistungen der Schüler/innen im Verhältnis zu ihren jeweiligen Testpopulationen vergleichen.
Die Standardnorm wird in der Qualitätskontrolle verwendet
Diese Norm ist bekannt dafür, dass sie für die Überwachung der Produktqualität in der Produktion wichtig ist. Durch eine genaue Betrachtung der Wahrscheinlichkeiten können die Hersteller feststellen, ob die Qualitätsschwankungen auf zufällige Schwankungen oder auf ein anderes Problem zurückzuführen sind. Das hängt mit den Hypothesentests zusammen, die wir bereits erwähnt haben, und auch mit einer Z-Score Tabelle, über die wir weiter unten sprechen werden.
Die Standardnormale wird in der statistischen Modellierung verwendet
Die Standardnormalverteilung spielt eine Rolle bei der Bewertung von Fehlern in Modellen wie der linearen Regression und der Zeitreihenprognose. Bei diesen Modellen gehen wir davon aus, dass die Residuen, also die Differenzen zwischen beobachteten und vorhergesagten Werten, nicht nur normalverteilt sind, sondern auch so standardisiert werden können, dass sie einer Standardnormalverteilung folgen.
Bei der linearen Regression sind standardisierte Residuen Residuen, die in standardisierte Werte umgewandelt wurden. Damit können wir messen, wie extrem ein Fehler in Standardabweichungseinheiten ist, was es einfacher macht, Ausreißer zu erkennen. Dies ist hilfreich, weil Heteroskedastizität in den Residuen, die in den Prädiktoren des Modells nicht offensichtlich sein kann, die Interpretation der Residuen verzerren kann.
Bei der Zeitreihenanalyse wird oft angenommen, dass die Prognosefehler einer Standardnormalverteilung folgen, wenn sie richtig standardisiert sind. Dies ist wichtig für die Erstellung von Vorhersageintervallen. Viele Zeitreihenmodelle, wie ARIMA, stützen sich auf Standard-Normalquantile, um Konfidenzgrenzen für Prognosen zu definieren. Auch wird bei der Zerlegung von Zeitreihen die Restkomponente, die unregelmäßige Schwankungen erfasst, oft als normalverteilt angesehen. Wenn du diese Restkomponente standardisierst, kannst du die Wahrscheinlichkeit von Extremwerten in deiner Zeitreihe ermitteln, von denen du weißt, dass sie nicht das Ergebnis des Trendzyklus oder der Saisonalität sind. In unserem Kurs "Forecasting in R" lernst du diese Art von Techniken.
Die Standardnormale wird beim maschinellen Lernen verwendet
Viele Algorithmen für maschinelles Lernen funktionieren am besten, wenn die Daten eine Standardgröße haben. Ich denke da an logistische Regression, k-means Clustering und neuronale Netze.
Ich denke dabei auch an die Hauptkomponentenanalyse, die oft als Vorverarbeitungstechnik verwendet wird. Bei der PCA wollen wir, dass unsere Eingangsmerkmale einen Mittelwert von Null und eine Einheitsvarianz haben, damit verhindert, dass Merkmale mit großen Werten dominieren. Ein üblicher Vorverarbeitungsschritt ist die Standardisierung der Daten, indem der Mittelwert abgezogen und durch die Standardabweichung geteilt wird. Dadurch wird sichergestellt, dass jedes Merkmal einen Mittelwert von Null und eine Einheitsvarianz hat. Es sollte jedoch klar sein, dass dadurch keine Normalität erzwungen wird. In manchen Fällen erwarte ich jedoch, dass die transformierten Daten sich der Normalität annähern, wenn die ursprüngliche Verteilung bereits annähernd normal ist.
Die Standardnorm wird für Wahrscheinlichkeitsberechnungen verwendet
Die kumulative Verteilungsfunktion der Standardnormalverteilung, über die wir vorhin gesprochen haben, ist gut tabelliert, d.h. sie ist vorberechnet und in allgemein zugänglichen Tabellen organisiert, was Wahrscheinlichkeitsberechnungen einfacher macht, weil du nur die Tabelle benutzen musst, um den richtigen Wert nachzuschlagen.
Um zum Beispiel die Wahrscheinlichkeit zu ermitteln, dass eine zufällig gewählte Körpergröße unter 1,80 m liegt, standardisieren wir die Körpergröße anhand der Normalverteilung der Grundgesamtheit und schlagen den Z-Score in einer Standardnormaltabelle nach. Ich habe eine Version der normalen Tabelle am Ende dieses Artikels eingefügt, falls du sie brauchen solltest.
Transformationen zur Anpassung von Daten an die Standard-Normalverteilung
Transformationen können dabei helfen, Daten in eine Standard-Normalverteilung umzuformen. Grob gesagt, wäre das ein zweiteiliger Prozess. Zuerst würden wir unsere Daten so umformen, dass sie normal werden, und dann würden wir eine Z-Score-Standardisierung durchführen.
Beachte, dass du die Z-Score-Standardisierung normalerweise nicht als ersten Schritt anwenden würdest, da Extremwerte die Standardabweichung verzerren können, da der Mittelwert und die Standardabweichung empfindlich auf Ausreißer reagieren. Außerdem erfordern einige Umwandlungen positive Daten. Wenn du zuerst die Z-Score-Standardisierung anwendest, können die mittelwertzentrierten Werte negative Zahlen enthalten, was bei Transformationen, die nur mit positiven Werten funktionieren, zu Problemen führen kann. Ich denke dabei speziell an Logarithmen. Es ist also am besten, wenn du der Reihe nach vorgehst: Schritt 1, dann Schritt 2.
Schritt 1: Daten umwandeln, um normal zu werden
Einige Ideen für die Umwandlung, die du verwenden könntest, sind:
Log-Transformation für schiefe Daten
Wenn Daten positiv verzerrt sind, kann eine Log-Transformation helfen, sie zu normalisieren. Wenn du zum Beispiel den Logarithmus auf Rohwerte anwendest, werden große Werte komprimiert, wodurch die Schiefe verringert und eine symmetrischere Verteilung geschaffen wird.
Quadratwurzeltransformation für Zähldaten
Bei Zähldaten oder mäßig schiefen Datensätzen können wir eine Quadratwurzeltransformation versuchen. Diese Methode verringert die Variabilität und erhält gleichzeitig eine symmetrischere Struktur, die die Daten näher an die Glockenkurvenform bringt.
Box-Cox-Transformation für flexible Anpassungen
Die Box-Cox-Transformation geht noch einen Schritt weiter, indem sie die Transformation an die Daten anpasst. Ihr Parameter λ bestimmt die genaue Formel, die angewandt wird, und macht sie sehr vielseitig für die Anpassung von Daten an die Eigenschaften der Standardnormalverteilung. Feature Engineering in R zeigt dir die Box-Cox-Methode, neben vielen anderen wichtigen und nützlichen Methoden.
Schritt 2: Z-Score-Standardisierung durchführen
Sobald eine Transformation durchgeführt wurde, können die Daten so standardisiert werden, dass sie der Standardnormalverteilung entsprechen. Dadurch werden die Daten so angepasst, dass sie einen Mittelwert von Null und eine Standardabweichung von Eins haben. Die Z-Score-Formel lautet:
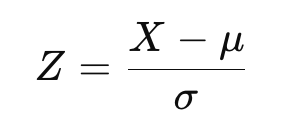
wobei X sind die transformierten Daten, μ ist der Mittelwert, und σ die Standardabweichung ist.
Wenn du mit der Unterscheidung zwischen Populations-Z-Score und Stichproben-Z-Score vertraut bist, wie wir sie in unserem Lernpfad zu statistischen Schlussfolgerungen in R behandeln, erkennst du die obige Gleichung vielleicht als die Gleichung für einen Populations-Z-Score. Wenn du mit einer Stichprobe und nicht mit der gesamten Grundgesamtheit arbeitest, würden wir stattdessen den Mittelwert und die Standardabweichung schätzen:
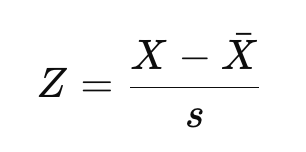
Dabei ist X-bar der Mittelwert der Stichprobe und s die Standardabweichung der Stichprobe.
Das Ergebnis wäre das gleiche, wenn du den Mittelwert und die Standardabweichung aus dem neuen, normalisierten Datensatz verwenden würdest. Manchmal sind Forscher aber auch daran interessiert, die Daten mit einer größeren Referenzpopulation zu vergleichen, indem sie stattdessen eine Art Benchmark-Mittelwert und Standardabweichung verwenden.
Stell dir vor, du betrachtest einen Einkommensdatensatz, der rechtsschief ist, und machst eine Log-Transformation, um ihn zu normalisieren. In diesem Fall würden wir den nationalen Mittelwert und die Standardabweichung anstelle der Werte aus unserer Stichprobe verwenden, um die Z-Werte zu berechnen. Der Zweck ist, einen aussagekräftigen Vergleich zwischen verschiedenen Datensätzen oder Studien zu ermöglichen.
Wenn du also eine Stichprobe verwendest, erhältst du technisch gesehen eine standardisierte Normalannäherung und nicht die exakte theoretische Standardnormalverteilung. Ich denke, diese Unterscheidung ist es wert, geklärt zu werden, auch wenn der Unterschied bei großen Datensätzen gering sein muss.
Visualisierung der Standard-Normalverteilung
Hier ist eine Möglichkeit, eine theoretische Standard-Normalverteilung in der Programmiersprache R zu erstellen. In diesem Code habe ich auch vertikale Linien für die Standardwerte, auch Z-Scores genannt, hinzugefügt.Auf kannst du für jeden beliebigen Wert sehen, wie viele Standardabweichungen über oder unter dem Mittelwert der Bevölkerung unser Wert liegt .
install.packages("ggplot2")
library(ggplot2)
ggplot(data.frame(x = c(-4, 4)), aes(x)) +
stat_function(fun = dnorm, geom = "area", fill = '#ffe6b7', color = 'black', alpha = 0.5, args = list( mean = 0, sd = 1)) +
labs(title = "Standard Normal Distribution", subtitle = "Standard Deviations and Z-Scores") +
theme(plot.title = element_text(hjust = 0.5, face = "bold")) +
theme(plot.subtitle = element_text(hjust = 0.5)) +
geom_vline(xintercept = 1, linetype = 'dotdash', color = "black") +
geom_vline(xintercept = -1, linetype = 'dotdash', color = "black") +
geom_vline(xintercept = 2, linetype = 'dotdash', color = "black") +
geom_vline(xintercept = -2, linetype = 'dotdash', color = "black") +
geom_vline(xintercept = 3, linetype = 'dotdash', color = "black") +
geom_vline(xintercept = -3, linetype = 'dotdash', color = "black") +
geom_text(aes(x=1, label="\n 1 σ", y=0.125), colour="#376795", angle=90, text=element_text(size=11)) +
geom_text(aes(x=2, label="\n 2 σ", y=0.125), colour="#376795", angle=90, text=element_text(size=11)) +
geom_text(aes(x=3, label="\n 3 σ", y=0.125), colour="#376795", angle=90, text=element_text(size=11)) +
geom_text(aes(x=-1, label="\n-1 σ", y=0.125), colour="#376795", angle=90, text=element_text(size=11)) +
geom_text(aes(x=-2, label="\n-2 σ", y=0.125), colour="#376795", angle=90, text=element_text(size=11)) +
geom_text(aes(x=-3, label="\n-3 σ", y=0.125), colour="#376795", angle=90, text=element_text(size=11))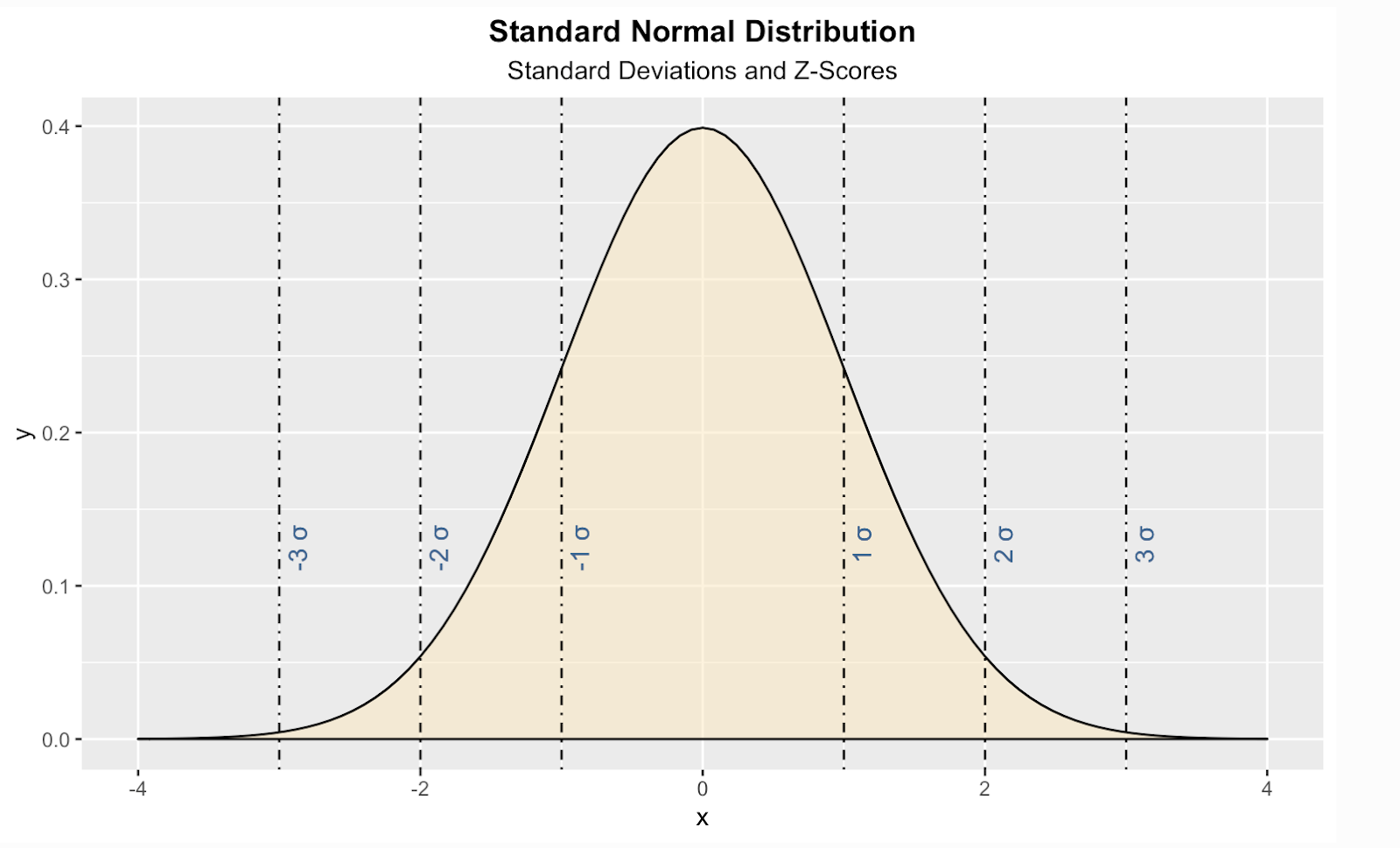
Du solltest wissen, dass es einige ähnliche Verteilungen gibt, die wie die Standardnormalverteilung aussehen können, es aber nicht sind:
| Vertrieb | Warum es nicht normal ist |
|---|---|
| t-Distribution | Etwas schwerere Schwänze, abhängig von den Freiheitsgraden |
| Logistische Verteilung | Etwas schwerere Schwänze als normal, andere Form |
| Laplace-Verteilung | Schärfere Spitze, stärkere Ausläufer, exponentieller Zerfall |
Die Standard-Normalverteilung und die Standard-Normal-Tabelle
Nun möchte ich auf etwas zurückkommen, das ich bereits erwähnt habe: die Idee einer Standardnormaltabelle, auch Z-Score-Tabelle oder Z-Tabelle genannt, die verwendet wird, um kumulative Wahrscheinlichkeiten für einen Z-Score zu finden, der die Anzahl der Standardabweichungen eines Wertes vom Mittelwert in einer Standardnormalverteilung darstellt. Diese Tabelle wird in der Statistik häufig für Hypothesentests, Konfidenzintervalle und Wahrscheinlichkeitsberechnungen verwendet. Anstatt die Wahrscheinlichkeiten manuell zu berechnen, kannst du anhand der Tabelle schnell den Anteil der Werte ermitteln, die unter einen bestimmten Z-Score fallen.
Es braucht etwas Übung, um die Tabelle zu lesen, und die Tabellen sehen manchmal anders aus als sonst. Hier siehst du sie in einem zweidimensionalen Format strukturiert. Das soll es einfacher machen, Wahrscheinlichkeiten für Z-Werte nachzuschlagen, wenn du mit Nachkommastellen arbeitest. In diesem Fall enthält die Spalte ganz links die ganze Zahl und die erste Dezimalstelle des Z-Scores. Die oberste Zeile steht für die zweite Nachkommastelle. Um die Wahrscheinlichkeit eines bestimmten Z-Scores zu ermitteln, suche die Zeile, die dem ersten Teil des Z-Scores entspricht, und dann die Spalte, die der zweiten Dezimalstelle entspricht. Der Wert am Schnittpunkt dieser Zeile und Spalte ist die kumulative Wahrscheinlichkeit, d. h. der Anteil der Datenpunkte, die unter diesen Z-Score fallen.
Am besten ist es, ein Beispiel zu zeigen: Angenommen, du berechnest einen Z-Score von 0,32 für das Testergebnis eines Schülers. Das bedeutet, dass der Wert 0,32 Standardabweichungen über dem Mittelwert liegt. Benutzen wir nun die Z-Tabelle, um die Wahrscheinlichkeit zu ermitteln, dass ein zufällig ausgewählter Wert kleiner als dieser Z-Wert ist.
- Schritt 1: Finde die Zeile für 0,3.
- Schritt 2: Finde die Spalte für 0,02.
- Schritt 3: Schau dir den Schnittpunkt der Zeile für 0,3 und der Spalte für 0,02 an. Der Wert an dieser Stelle ist 0,6915.
Die kumulative Wahrscheinlichkeit für Z = 0,32 beträgt 0,6554, was bedeutet, dass 65,54 % der Werte in einer Standardnormalverteilung weniger als 0,32 Standardabweichungen über dem Mittelwert liegen. Wenn du die Wahrscheinlichkeit bestimmen musst, dass ein Wert größer als ein bestimmter Z-Wert ist, ziehst du den Wert der Tabelle von 1 ab, bevor du die Zeile und die Spalte findest.
| Z | 0.01 | 0.02 | 0.03 | 0.04 | 0.05 | 0.06 | 0.07 | 0.08 | 0.09 |
|---|---|---|---|---|---|---|---|---|---|
| 0.1 | 0.5793 | 0.6179 | 0.6554 | 0.6915 | 0.7257 | 0.7580 | 0.7881 | 0.8159 | 0.8413 |
| 0.2 | 0.6179 | 0.6554 | 0.6915 | 0.7257 | 0.7580 | 0.7881 | 0.8159 | 0.8413 | 0.8643 |
| 0.3 | 0.6554 | 0.6915 | 0.7257 | 0.7580 | 0.7881 | 0.8159 | 0.8413 | 0.8643 | 0.8849 |
| 0.4 | 0.6915 | 0.7257 | 0.7580 | 0.7881 | 0.8159 | 0.8413 | 0.8643 | 0.8849 | 0.9032 |
| 0.5 | 0.7257 | 0.7580 | 0.7881 | 0.8159 | 0.8413 | 0.8643 | 0.8849 | 0.9032 | 0.9192 |
| 0.6 | 0.7580 | 0.7881 | 0.8159 | 0.8413 | 0.8643 | 0.8849 | 0.9032 | 0.9192 | 0.9332 |
| 0.7 | 0.7881 | 0.8159 | 0.8413 | 0.8643 | 0.8849 | 0.9032 | 0.9192 | 0.9332 | 0.9452 |
| 0.8 | 0.8159 | 0.8413 | 0.8643 | 0.8849 | 0.9032 | 0.9192 | 0.9332 | 0.9452 | 0.9554 |
| 0.9 | 0.8413 | 0.8643 | 0.8849 | 0.9032 | 0.9192 | 0.9332 | 0.9452 | 0.9554 | 0.9641 |
| 1.0 | 0.8643 | 0.8849 | 0.9032 | 0.9192 | 0.9332 | 0.9452 | 0.9554 | 0.9641 | 0.9713 |
Fazit
Ich hoffe, dir hat diese Erkundung der Standard-Normalverteilung gefallen. Lerne weiter mit uns hier im DataCamp. Ich habe bereits unseren Kurs "Einführung in die Statistik in R" und unseren Lernpfad " Statistische Inferenz in R " erwähnt. Wenn du aber Python bevorzugst, sind unser Kurs Statistisches Denken in Python und unser Kurs Versuchsplanung in Python eine gute Wahl.

FAQs zur Standard-Normalverteilung
Wie unterscheidet sich die Standard-Normalverteilung von einer Normalverteilung?
Die Standardnormalverteilung ist ein Sonderfall der Normalverteilung, bei der der Mittelwert 0 und die Standardabweichung 1 ist. Diese Standardisierung ermöglicht einfachere Wahrscheinlichkeitsberechnungen und Vergleiche zwischen verschiedenen Datensätzen.
Ergibt das Subtrahieren des Mittelwerts und das Dividieren durch die Standardabweichung eine Standardnormalverteilung?
Durch Subtraktion des Mittelwerts und Division durch die Standardabweichung wird ein Datensatz in eine standardisierte Form umgewandelt, aber es entsteht nicht unbedingt eine Standardnormalverteilung, es sei denn, die ursprünglichen Daten waren normal verteilt.
Welcher Zusammenhang besteht zwischen der Standardnormalverteilung und dem zentralen Grenzwertsatz?
Der zentrale Grenzwertsatz besagt, dass die Summe vieler unabhängiger, identisch verteilter Zufallsvariablen dazu tendiert, einer Normalverteilung zu folgen, die auf die Standardnormalform normiert werden kann.
Was bedeutet ein Z-Score in der Standardnormalverteilung?
Ein Z-Score gibt an, wie viele Standardabweichungen ein Wert vom Mittelwert abweicht. Ein positiver Z-Score bedeutet, dass der Wert über dem Mittelwert liegt, während ein negativer Z-Score bedeutet, dass er darunter liegt.
Was hat die Standardnormalverteilung mit Konfidenzintervallen zu tun?
Konfidenzintervalle verwenden Z-Werte, um Wahrscheinlichkeitsbereiche für die Schätzung von Populationsparametern zu bestimmen. Ein 95%iges Konfidenzintervall entspricht zum Beispiel Z-Werten von etwa ±1,96.
