Comprender la ecuación de Bellman en el aprendizaje por refuerzo

A principios de los años 50, Richard Bellman, un matemático e informático visionario, se embarcó en un viaje para desentrañar las complejidades de la toma de decisiones en entornos inciertos. Impulsado por la necesidad de métodos eficaces de resolución de problemas, introdujo el revolucionario concepto de programación dinámica, que descompone los problemas intrincados en subproblemas manejables. 

Al explorar este enfoque, Bellman formuló lo que más tarde se conocería como la Ecuación de Bellman: una expresión matemática que evalúa el valor de una decisión en un estado determinado basándose en los posibles estados futuros y sus recompensas asociadas. Su trabajo pionero culminó con la publicación de su libro de 1957, Dynamic Programming, que sentó las bases teóricas de la teoría de la optimización y el control, al tiempo que allanaba el camino para los avances en inteligencia artificial y aprendizaje por refuerzo.

Hoy en día, las ideas de Bellman siguen dando forma a la forma en que las máquinas aprenden y se adaptan a su entorno, dejando un legado duradero en las matemáticas y la informática. En el aprendizaje por refuerzo, la Ecuación de Bellman es crucial para comprender cómo interactúan los agentes con su entorno, por lo que resulta esencial para resolver diversos problemas en Procesos de Decisión de Markov (MDP). 

En este artículo, exploraremos qué es la ecuación, cómo se compara con la Ecuación de Optimalidad de Bellman, cómo se utiliza en el aprendizaje por refuerzo y mucho más.

¿Qué es la Ecuación de Bellman?

La Ecuación de Bellman es una fórmula recursiva utilizada en la toma de decisiones y en el aprendizaje por refuerzo. Muestra cómo el valor de estar en un determinado estado depende de las recompensas recibidas y del valor de los estados futuros. 

En términos sencillos, la Ecuación de Bellman descompone un problema complejo en pasos más pequeños, lo que facilita su resolución. La ecuación ayuda a encontrar la mejor forma de tomar decisiones cuando los resultados dependen de una serie de acciones.

Matemáticamente, la Ecuación de Bellman se escribe como:

Dónde:

• V(s): El valor del estado sss, que representa la recompensa a largo plazo de estar en ese estado.
• R(s,a): La recompensa inmediata recibida por realizar una acción aaa en el estado sss.
• γ: El factor de descuento (entre 0 y 1) que determina la importancia de las recompensas futuras en comparación con las recompensas inmediatas.
• P(s′∣s,a) La probabilidad de pasar al estado s′ desde el estado sss mediante la acción a.
• max⁡a​: La acción óptima que maximiza el valor esperado de las recompensas futuras.

Esta suma multiplica el valor de cada posible estado siguiente por la probabilidad de llegar a ese estado, capturando efectivamente las recompensas futuras esperadas.

Ecuación de Bellman vs. Ecuación de optimalidad de Bellman

La Ecuación de Bellman calcula el valor de un estado basándose en las recompensas de realizar acciones y en el valor esperado de los estados futuros. Es una parte clave para evaluar lo buena que es una política cuando un agente la sigue en un entorno. La ecuación considera todas las acciones y resultados posibles y ayuda a determinar el valor de estar en un determinado estado.

En cambio, la Ecuación de Optimalidad de Bellman se utiliza cuando el objetivo es encontrar la política mejor u "óptima". 

En lugar de limitarse a evaluar el valor de un estado basándose en una política concreta, encuentra el valor máximo alcanzable considerando todas las acciones y políticas posibles. La Ecuación de Optimalidad de Bellman lo hace tomando la máxima recompensa esperada sobre todas las acciones disponibles en cada estado. De este modo, nos indica el mayor valor posible que podemos obtener de cada estado si actuamos de la mejor manera posible.

En otras palabras, la principal diferencia entre las dos ecuaciones es su enfoque.

La Ecuación de Bellman estándar evalúa la eficacia de una política estimando el valor esperado de seguirla. Por otro lado, la Ecuación de Optimalidad de Bellman tiene como objetivo encontrar la mejor política en general identificando la acción que proporciona la máxima recompensa a largo plazo en cada estado. 

TLDR: La Ecuación de Bellman estándar se utiliza para la evaluación de la política, mientras que la ecuación de optimalidad se utiliza para la mejora y el control de la política.

La Ecuación de Optimalidad de Bellman es esencial para resolver problemas de control, en los que el objetivo es elegir la mejor secuencia de acciones para maximizar las recompensas. En estos problemas, los agentes deben tomar decisiones que maximicen las recompensas inmediatas y tengan en cuenta las recompensas futuras. 

La ecuación de optimalidad proporciona una forma de evaluar y elegir sistemáticamente las acciones que conducen a la mayor recompensa posible a largo plazo, ayudando a encontrar la política óptima. Es una parte central de algoritmos como aprendizaje Q y la iteración de valores, que se utilizan en el aprendizaje por refuerzo para entrenar a los agentes a actuar de la mejor manera posible.

Ecuación de Bellman en el aprendizaje por refuerzo

La Ecuación de Bellman es una parte fundamental del aprendizaje por refuerzo. Ayuda a los agentes a aprender a tomar las mejores decisiones dividiendo las tareas complejas en pasos más pequeños.

En concreto, la Ecuación de Bellman permite a los agentes calcular el valor de diferentes estados y acciones, lo que les guía en la elección del mejor camino para maximizar las recompensas. 

Así, en el aprendizaje por refuerzo, la Ecuación de Bellman se utiliza para evaluar y mejorar las políticas, garantizando que los agentes tomen mejores decisiones a medida que adquieren experiencia.

Papel en Q-Learning

El aprendizaje Q es un algoritmo popular de aprendizaje por refuerzo. El algoritmo aprovecha la Ecuación de Bellman para estimar el valor de los pares estado-acción, conocidos como valores Q. Estos valores indican al agente lo gratificante que será realizar una determinada acción en un estado dado y seguir después la mejor política. 

La Ecuación de Optimalidad de Bellman para el aprendizaje Q encuentra el valor máximo esperado para cada acción, ayudando a los agentes a identificar los mejores movimientos para maximizar sus recompensas a largo plazo.

Por ejemplo, en un problema de aprendizaje episódico por refuerzo, imagina un agente que navega por un mundo cuadriculado. Cuando alcanza un estado, el agente actualiza su valor Q para ese par estado-acción utilizando la ecuación:

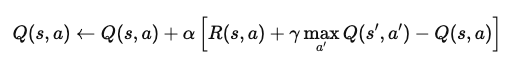
Dónde:

• Q(s,a): El valor Q para realizar la acción a en el estado s.
• α: La tasa de aprendizaje, que determina cuánta información nueva anula el valor Q antiguo.
• R(s,a): La recompensa inmediata recibida tras realizar la acción a en el estado s.
• γ: El factor de descuento, que pondera las recompensas futuras en relación con las recompensas inmediatas.
• maxa′Q(s′,a′): El valor Q máximo para el siguiente estado s′, en todas las acciones posibles a′.

Esta ecuación actualiza el valor Q en función de la recompensa inmediata y de las recompensas futuras máximas esperadas. Mediante la aplicación repetida, el agente aprende a aproximarse a los valores Q óptimos y puede determinar las mejores acciones para maximizar las recompensas a largo plazo.

Ecuación de Bellman para la evaluación de políticas

La Ecuación de Bellman también se utiliza para evaluar políticas mediante la estimación de funciones de valor. En este contexto, calcula la recompensa esperada a largo plazo cuando un agente sigue una política determinada a partir de un estado específico. Esto ayuda a determinar la eficacia de una política mostrando la recompensa media que puede esperar el agente.

El algoritmo de iteración de políticas utiliza esta evaluación para mejorar las políticas. Empieza estimando la función de valor de una política y luego actualiza la política para elegir mejores acciones basándose en este valor. Este proceso se repite hasta que la política converge a la óptima, momento en el que ya no se pueden hacer más mejoras. 

Derivación de la ecuación de Bellman

En esta sección, desglosaremos la Ecuación de Bellman paso a paso, partiendo de los primeros principios. Luego exploraremos cómo las recompensas y las transiciones construyen funciones de valor, guiando a los agentes en la elección de las mejores acciones.

Derivación paso a paso

Para derivar la Ecuación de Bellman, partimos del concepto de función de valor. La función de valor, V(s)V(s)V(s), da la recompensa acumulada esperada por empezar en un estado sss y seguir una política óptima a partir de entonces. Esta ecuación es recursiva, es decir, relaciona el valor de un estado con el valor de los estados siguientes.

1. Define la función valor

La función de valor V(s) representa la recompensa total esperada que recibirá un agente por empezar en el estado sss y seguir la política óptima. Matemáticamente, puede expresarse como:

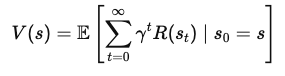
Dónde:

• s es el estado actual,
• γ es el factor de descuento (entre 0 y 1), que controla la importancia de las recompensas futuras,
• R(st) es la recompensa recibida en cada paso temporal t.

2. Desglosar las recompensas futuras

Expresar V(s) en términos de recompensas inmediatas y del valor de los estados futuros, separamos la primera recompensa de la suma de todas las recompensas futuras:

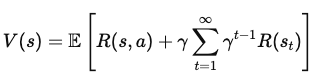
Dónde:

• R(s, a) es la recompensa inmediata obtenida al realizar la acción a en el estado s,
• γ Σ (γ(t1)) R(st) representa la suma descontada de las recompensas futuras.

3. Incorpora el siguiente valor de estado

Ahora añadimos el valor del siguiente estado, s', al que llega el agente tras realizar la acción a en el estado s. Esto nos lleva a la ecuación

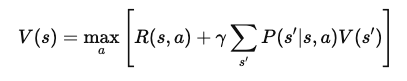
Dónde:

• P(s' | s, a) es la probabilidad de pasar al estado s' desde el estado s tras realizar la acción a,
• maxa representa la elección de la acción a que maximiza la recompensa esperada.

4. La ecuación final de Bellman

Después de simplificar, la Ecuación de Bellman para la función de valor V(s) se convierte en

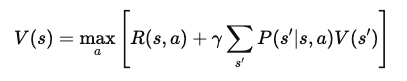
Esta forma final de la Ecuación de Bellman descompone el valor de un estado en dos componentes: la recompensa inmediata y el valor esperado del siguiente estado. Esta estructura recursiva permite a los algoritmos calcular o aproximar V(s) de forma iterativa, lo que ayuda a encontrar políticas óptimas a lo largo del tiempo.

Ejemplos y aplicaciones

Veamos un ejemplo con un mundo cuadriculado sencillo:

Imagina un agente que intenta alcanzar un objetivo en una cuadrícula mientras evita obstáculos. El agente se mueve hacia arriba, abajo, izquierda o derecha y obtiene recompensas por cada movimiento. Si alcanza el objetivo, obtiene una recompensa mayor. Utilizando la Ecuación de Bellman, podemos calcular el valor de cada estado de la red evaluando las recompensas inmediatas y los valores de los estados futuros.

Para Procesos de Decisión de Markov (MDP), la Ecuación de Bellman ayuda a encontrar la política óptima. Si tenemos un MDP pequeño, como un problema de entrega en el que un agente debe elegir la ruta más rápida, aplicamos la ecuación a cada par estado-acción. Al hacerlo, podemos calcular las mejores acciones que maximizan la recompensa total esperada. 

Temas avanzados: Ecuación de Bellman en el aprendizaje Q

En esta sección, exploramos cómo se aplica la Ecuación de Bellman en métodos avanzados como:

• Iteración de valores
• Aprendizaje por diferencia temporal. 

Estas técnicas ayudan a los agentes a aprender acciones óptimas actualizando las estimaciones de valor, incluso en entornos complejos. Comprender estos temas avanzados es clave para dominar el aprendizaje por refuerzo.

Iteración de valores

La iteración de valores es un método que utiliza la Ecuación de Bellman para actualizar las funciones de valor de forma iterativa. El objetivo es encontrar el valor óptimo de cada estado para que el agente pueda determinar las mejores acciones. 

En la iteración de valores, el agente actualiza el valor de cada estado basándose en los posibles estados futuros y sus recompensas. Este proceso se repite hasta que los valores convergen en una solución estable. Las propiedades de convergencia de la iteración del valor garantizan que, dado el tiempo suficiente, encontrará la política óptima.

Aprendizaje por diferencia temporal

El aprendizaje TD es otro enfoque que utiliza la Ecuación de Bellman, pero difiere en un aspecto clave: no necesita un modelo del entorno. 

En lugar de ello, actualiza las estimaciones de valor basándose en las experiencias reales que recoge el agente. Esto lo hace más práctico cuando el entorno es desconocido. El aprendizaje TD tiende un puente entre los métodos de Montecarlo, que se basan en episodios completos, y la programación dinámica, que necesita un modelo completo.

Aplicaciones y casos de uso

La Ecuación de Bellman tiene una amplia gama de aplicaciones más allá de los modelos teóricos. Desempeña un papel crucial en escenarios del mundo real en los que es necesario tomar decisiones y optimizar. Esta sección explora cómo la Ecuación de Bellman admite estas aplicaciones.

Aprendizaje por refuerzo en los juegos

En entornos de juego clásicos como Atari, la Ecuación de Bellman ayuda a optimizar las acciones de un agente para conseguir la mayor puntuación. La ecuación guía al agente en la selección de los mejores movimientos evaluando las recompensas esperadas de cada acción. 

Los ejemplos del mundo real incluyen el uso de algoritmos profundos de aprendizaje por refuerzo, como las Redes Q Profundas (DQN), que utilizan la Ecuación de Bellman para mejorar la IA de los juegos. Estos métodos se han utilizado para entrenar agentes que superan a los jugadores humanos en varios juegos, lo que demuestra el poder del aprendizaje por refuerzo.

Robótica y navegación

En robótica, la Ecuación de Bellman ayuda a las máquinas a tomar decisiones sobre el movimiento y la navegación. Los robots la utilizan para evaluar distintos caminos y elegir el que maximiza las recompensas futuras, como alcanzar un objetivo en el menor tiempo o con la menor energía. 

En otras palabras, los robots utilizan la ecuación de Bellman para ayudarles a predecir los resultados basándose en su estado actual y planificar sus próximos movimientos en consecuencia. Este proceso de toma de decisiones es fundamental para navegar por un laberinto o evitar obstáculos en entornos dinámicos.

Conclusión

La Ecuación de Bellman es fundamental en el desarrollo de sistemas inteligentes, sobre todo en el aprendizaje por refuerzo y otras áreas de la inteligencia artificial. Sirve de base para algoritmos que permiten a los sistemas aprender, adaptarse y optimizar sus acciones en entornos dinámicos, lo que conduce a una resolución de problemas más eficiente y eficaz en entornos inciertos. 

Aquí tienes algunos recursos para continuar tu aprendizaje: 

• Aprendizaje por Refuerzo con Gymnasium en Python 
• Aprendizaje por Refuerzo: Una introducción con ejemplos en Python
• Algoritmo de aprendizaje por refuerzo SARSA en Python: Una guía completa
• Qué es el aprendizaje por refuerzo a partir de la retroalimentación humana 
• RLAIF: ¿Qué es el aprendizaje por refuerzo a partir de la retroalimentación de la IA?