Entendendo a equação de Bellman no aprendizado por reforço

No início da década de 1950, Richard Bellman, um visionário matemático e cientista da computação, embarcou em uma jornada para desvendar as complexidades da tomada de decisões em ambientes incertos. Motivado pela necessidade de métodos eficientes de solução de problemas, ele introduziu o conceito revolucionário de programação dinâmica, que divide problemas complexos em subproblemas gerenciáveis. 

Ao explorar essa abordagem, Bellman formulou o que mais tarde seria conhecido como a Equação de Bellman: uma expressão matemática que avalia o valor de uma decisão em um determinado estado com base nos possíveis estados futuros e suas recompensas associadas. Seu trabalho inovador culminou com a publicação do livro de 1957, Dynamic Programming, que estabeleceu a base teórica para a teoria de otimização e controle, abrindo caminho para os avanços em inteligência artificial e aprendizado por reforço.

Hoje, as ideias de Bellman continuam a moldar a forma como as máquinas aprendem e se adaptam a seus ambientes, deixando um legado duradouro na matemática e na ciência da computação. Na aprendizagem por reforço, a equação de Bellman é fundamental para entender como os agentes interagem com o ambiente, o que a torna essencial para resolver vários problemas em processos de decisão de Markov (MDPs). 

Neste artigo, exploraremos o que é essa equação, como ela se compara à equação de otimização de Bellman, como ela é usada no aprendizado por reforço e muito mais.

O que é a equação de Bellman?

A equação de Bellman é uma fórmula recursiva usada na tomada de decisões e no aprendizado por reforço. Ele mostra como o valor de estar em um determinado estado depende das recompensas recebidas e do valor dos estados futuros. 

Em termos simples, a equação de Bellman divide um problema complexo em etapas menores, o que facilita a solução. A equação ajuda a encontrar a melhor maneira de tomar decisões quando os resultados dependem de uma série de ações.

Matematicamente, a equação de Bellman é escrita como:

Onde:

• V(s): O valor do estado sss, que representa a recompensa de longo prazo de estar nesse estado.
• R(s,a): A recompensa imediata recebida por realizar a ação aaa no estado sss.
• γ: O fator de desconto (entre 0 e 1) que determina a importância das recompensas futuras em comparação com as recompensas imediatas.
• P(s′∣s,a) A probabilidade de transição para o estado s′ do estado sss por meio da ação a.
• max⁡a​: A ação ideal que maximiza o valor esperado de recompensas futuras.

Essa soma multiplica o valor de cada estado seguinte possível pela probabilidade de atingir esse estado, capturando efetivamente as recompensas futuras esperadas.

Equação de Bellman vs. Equação de otimização de Bellman

A equação de Bellman calcula o valor de um estado com base nas recompensas de ações e no valor esperado de estados futuros. É uma parte fundamental da avaliação da qualidade de uma política quando um agente a segue em um ambiente. A equação analisa todas as ações e resultados possíveis e ajuda a determinar o valor de estar em um determinado estado.

Em contrapartida, a equação de otimização de Bellman é usada quando o objetivo é encontrar a melhor política ou a política "ideal". 

Em vez de apenas avaliar o valor de um estado com base em uma política específica, ele encontra o valor máximo que pode ser alcançado considerando todas as ações e políticas possíveis. A equação de otimização de Bellman faz isso usando a recompensa máxima esperada em todas as ações disponíveis em cada estado. Dessa forma, ele nos informa o maior valor possível que podemos obter de cada estado se agirmos da melhor maneira possível.

Em outras palavras, a principal diferença entre as duas equações é o foco.

A equação de Bellman padrão avalia a eficácia de uma política estimando o valor esperado de segui-la. Por outro lado, a equação de otimização de Bellman tem como objetivo encontrar a melhor política geral, identificando a ação que oferece a recompensa máxima de longo prazo em cada estado. 

TLDR: A equação de Bellman padrão é usada para avaliação de políticas, enquanto a equação de otimização é usada para aprimoramento e controle de políticas.

A equação de otimização de Bellman é essencial para resolver problemas de controle, em que o objetivo é escolher a melhor sequência de ações para maximizar as recompensas. Nesses problemas, os agentes precisam tomar decisões que maximizem as recompensas imediatas e considerem as recompensas futuras. 

A equação de otimização oferece uma maneira de avaliar e escolher sistematicamente as ações que levam à maior recompensa possível em longo prazo, ajudando a encontrar a política ideal. É uma parte central de algoritmos como Q-learning e iteração de valores, que são usados no aprendizado por reforço para treinar os agentes a agir da melhor maneira possível.

Equação de Bellman no aprendizado por reforço

A equação de Bellman é uma parte essencial do aprendizado por reforço. Ele ajuda os agentes a aprender como tomar as melhores decisões, dividindo tarefas complexas em etapas menores.

Ou seja, a equação de Bellman permite que os agentes calculem o valor de diferentes estados e ações, o que os orienta na escolha do melhor caminho para maximizar as recompensas. 

Assim, na aprendizagem por reforço, a equação de Bellman é usada para avaliar e aprimorar políticas, garantindo que os agentes tomem decisões melhores à medida que adquirem experiência.

Função no Q-Learning

O Q-learning é um algoritmo popular de aprendizado por reforço. O algoritmo aproveita a equação de Bellman para estimar o valor dos pares estado-ação, conhecidos como valores Q. Esses valores informam ao agente o quanto será recompensador realizar uma determinada ação em um determinado estado e seguir a melhor política posteriormente. 

A equação de otimização de Bellman para Q-learning encontra o valor máximo esperado para cada ação, ajudando os agentes a identificar os melhores movimentos para maximizar suas recompensas de longo prazo.

Por exemplo, em um problema de aprendizado por reforço episódico, imagine um agente navegando em um mundo de grade. Quando atinge um estado, o agente atualiza seu valor Q para esse par estado-ação usando a equação:

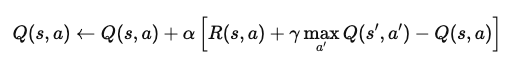
Onde:

• Q(s,a): O valor Q para realizar a ação a no estado s.
• α: A taxa de aprendizado, que determina a quantidade de novas informações que substituem o valor Q antigo.
• R(s,a): A recompensa imediata recebida após a ação a no estado s.
• γ: O fator de desconto, que pondera as recompensas futuras em relação às recompensas imediatas.
• max⁡a′Q(s′,a′): O valor Q máximo para o próximo estado s′, em todas as ações possíveis a′.

Essa equação atualiza o valor Q com base na recompensa imediata e nas recompensas futuras máximas esperadas. Com a aplicação repetida, o agente aprende a se aproximar dos valores Q ideais e pode determinar as melhores ações para maximizar as recompensas de longo prazo.

Equação de Bellman para avaliação de políticas

A equação de Bellman também é usada para avaliar políticas por meio da estimativa de funções de valor. Nesse contexto, ele calcula a recompensa esperada de longo prazo quando um agente segue uma determinada política a partir de um estado específico. Isso ajuda a determinar a eficácia de uma política, mostrando a recompensa média que o agente pode esperar.

O algoritmo de iteração de políticas usa essa avaliação para aprimorar as políticas. Ele começa estimando a função de valor de uma política e, em seguida, atualiza a política para escolher ações melhores com base nesse valor. Esse processo se repete até que a política converge para o ideal, quando então não é possível fazer mais melhorias. 

Derivação da equação de Bellman

Nesta seção, analisaremos a equação de Bellman passo a passo, começando pelos primeiros princípios. Em seguida, exploraremos como as recompensas e as transições criam funções de valor, orientando os agentes na escolha das melhores ações.

Derivação passo a passo

Para derivar a equação de Bellman, começamos com o conceito de uma função de valor. A função de valor, V(s)V(s)V(s), fornece a recompensa cumulativa esperada para começar em um estado sss e seguir uma política ideal depois disso. Essa equação é recursiva, o que significa que ela relaciona o valor de um estado ao valor dos estados subsequentes.

1. Definir a função de valor

A função de valor V(s) representa a recompensa total esperada que um agente receberá ao iniciar no estado sss e seguir a política ideal. Matematicamente, isso pode ser expresso como:

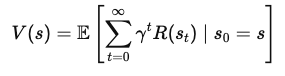
Onde:

• s é o estado atual,
• γ é o fator de desconto (entre 0 e 1), que controla a importância das recompensas futuras,
• R(st) é a recompensa recebida em cada etapa de tempo t.

2. Como você pode dividir as recompensas futuras

Para expressar V(s) em termos de recompensas imediatas e do valor de estados futuros, separamos a primeira recompensa da soma de todas as recompensas futuras:

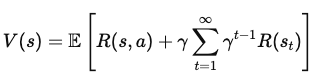
Onde:

• R(s, a) é a recompensa imediata obtida pela ação a no estado s,
• γ Σ (γ(t1)) R(st) representa a soma descontada das recompensas futuras.

3. Incorporar o próximo valor de estado

Agora, adicionamos o valor do próximo estado, s', que o agente atinge depois de realizar a ação a no estado s. Isso leva à equação:

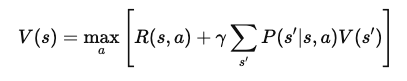
Onde:

• P(s' | s, a) é a probabilidade de transição para o estado s' a partir do estado s depois de realizar a ação a,
• máximoa representa a escolha da ação a que maximiza a recompensa esperada.

4. A equação final de Bellman

Após a simplificação, a equação de Bellman para a função de valor V(s) passa a ser:

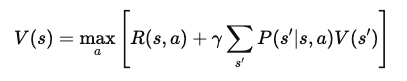
Essa forma final da equação de Bellman decompõe o valor de um estado em dois componentes: a recompensa imediata e o valor esperado do próximo estado. Essa estrutura recursiva permite que os algoritmos calculem ou aproximem V(s) iterativamente, o que ajuda a encontrar políticas ideais ao longo do tempo.

Exemplos e aplicações

Vamos ver um exemplo com um mundo de grade simples:

Imagine um agente tentando atingir uma meta em uma grade, evitando obstáculos. O agente se move para cima, para baixo, para a esquerda ou para a direita e recebe recompensas por cada movimento. Se você atingir a meta, receberá uma recompensa maior. Usando a equação de Bellman, podemos calcular o valor de cada estado na grade avaliando as recompensas imediatas e os valores de estados futuros.

Para processos de decisão de Markov (MDPs), a equação de Bellman ajuda a encontrar a política ideal. Se tivermos um MDP pequeno, como um problema de entrega em que um agente deve escolher a rota mais rápida, aplicaremos a equação a cada par estado-ação. Dessa forma, podemos calcular as melhores ações que maximizam a recompensa total esperada. 

Tópicos avançados: Equação de Bellman no Q-Learning

Nesta seção, exploramos como a equação de Bellman é aplicada em métodos avançados, como:

• Iteração de valores
• Aprendizado por diferença temporal. 

Essas técnicas ajudam os agentes a aprender ações ideais atualizando estimativas de valor, mesmo em ambientes complexos. Compreender esses tópicos avançados é fundamental para que você domine o aprendizado por reforço.

Iteração de valores

A iteração de valor é um método que usa a equação de Bellman para atualizar as funções de valor iterativamente. O objetivo é encontrar o valor ideal para cada estado para que o agente possa determinar as melhores ações. 

Na iteração de valores, o agente atualiza o valor de cada estado com base em possíveis estados futuros e suas recompensas. Esse processo se repete até que os valores convirjam para uma solução estável. As propriedades de convergência da iteração de valor garantem que, com tempo suficiente, você encontrará a política ideal.

Aprendizagem por diferença temporal

O aprendizado TD é outra abordagem que usa a equação de Bellman, mas difere em um aspecto fundamental: não precisa de um modelo do ambiente. 

Em vez disso, ele atualiza as estimativas de valor com base nas experiências reais que o agente reúne. Isso o torna mais prático quando o ambiente é desconhecido. O aprendizado TD preenche a lacuna entre os métodos de Monte Carlo, que dependem de episódios completos, e a programação dinâmica, que precisa de um modelo completo.

Aplicativos e casos de uso

A equação de Bellman tem uma ampla gama de aplicações além dos modelos teóricos. Ele desempenha um papel fundamental em cenários do mundo real em que a tomada de decisões e a otimização são necessárias. Esta seção explora como a equação de Bellman dá suporte a esses aplicativos.

Aprendizagem por reforço em jogos

Em ambientes de jogos clássicos como o Atari, a equação de Bellman ajuda a otimizar as ações de um agente para obter a pontuação mais alta. A equação orienta o agente na seleção dos melhores movimentos, avaliando as recompensas esperadas para cada ação. 

Exemplos do mundo real incluem o uso de algoritmos de aprendizagem por reforço profundo, como Deep Q-Networks (DQNs), que usam a equação de Bellman para aprimorar a IA de jogos. Esses métodos foram usados para treinar agentes que superam o desempenho de jogadores humanos em vários jogos, mostrando o poder do aprendizado por reforço.

Robótica e navegação

Na robótica, a equação de Bellman ajuda as máquinas a tomar decisões sobre movimento e navegação. Os robôs o utilizam para avaliar diferentes caminhos e escolher aquele que maximiza as recompensas futuras, como atingir uma meta no menor tempo possível ou com o mínimo de energia. 

Em outras palavras, os robôs usam a equação de Bellman para ajudá-los a prever resultados com base em seu estado atual e planejar seus próximos movimentos de acordo. Esse processo de tomada de decisão é essencial para navegar em um labirinto ou evitar obstáculos em ambientes dinâmicos.

Conclusão

A equação de Bellman é fundamental no desenvolvimento de sistemas inteligentes, especialmente no aprendizado por reforço e em outras áreas da inteligência artificial. Ele serve como base para algoritmos que permitem que os sistemas aprendam, se adaptem e otimizem suas ações em ambientes dinâmicos, o que leva a uma solução de problemas mais eficiente e eficaz em ambientes incertos. 

Aqui estão alguns recursos para você continuar aprendendo: 

• Aprendizado por reforço com o Gymnasium em Python 
• Aprendizagem por reforço: Uma introdução com exemplos em Python
• Algoritmo de aprendizado por reforço SARSA em Python: Um guia completo
• O que é o aprendizado por reforço a partir do feedback humano? 
• RLAIF: O que é aprendizado por reforço com feedback de IA?