Comprendre l'équation de Bellman dans l'apprentissage par renforcement

Au début des années 1950, Richard Bellman, mathématicien et informaticien visionnaire, s'est lancé dans un voyage visant à démêler les complexités de la prise de décision dans des environnements incertains. Poussé par le besoin de méthodes efficaces de résolution des problèmes, il a introduit le concept révolutionnaire de la programmation dynamique, qui décompose les problèmes complexes en sous-problèmes gérables. 

En explorant cette approche, Bellman a formulé ce qui sera plus tard connu sous le nom d'équation de Bellman : une expression mathématique qui évalue la valeur d'une décision dans un état donné en fonction des états futurs potentiels et des récompenses qui leur sont associées. Ses travaux novateurs ont abouti à la publication en 1957 de son livre, Dynamic Programming, qui a jeté les bases théoriques de l'optimisation et de la théorie du contrôle tout en ouvrant la voie aux progrès de l'intelligence artificielle et de l'apprentissage par renforcement. l'apprentissage par renforcement.

Aujourd'hui, les idées de Bellman continuent de façonner la manière dont les machines apprennent et s'adaptent à leur environnement, laissant un héritage durable dans les domaines des mathématiques et de l'informatique. Dans l'apprentissage par renforcement, l'équation de Bellman est cruciale pour comprendre comment les agents interagissent avec leur environnement, ce qui la rend essentielle pour résoudre divers problèmes dans les processus de décision de Markov (PDM). 

Dans cet article, nous verrons ce qu'est cette équation, comment elle se compare à l'équation d'optimalité de Bellman, comment elle est utilisée dans l'apprentissage par renforcement, et bien d'autres choses encore.

Qu'est-ce que l'équation de Bellman ?

L'équation de Bellman est une formule récursive utilisée dans la prise de décision et l'apprentissage par renforcement. Il montre comment la valeur d'être dans un certain état dépend des récompenses reçues et de la valeur des états futurs. 

En termes simples, l'équation de Bellman décompose un problème complexe en étapes plus petites, ce qui le rend plus facile à résoudre. L'équation permet de trouver la meilleure façon de prendre des décisions lorsque les résultats dépendent d'une série d'actions.

Mathématiquement, l'équation de Bellman s'écrit comme suit :

Où ?

• V(s): La valeur de l'état sss, qui représente la récompense à long terme d'être dans cet état.
• R(s,a): La récompense immédiate reçue pour l'action aaa dans l'état sss.
• γ : Le facteur d'actualisation (entre 0 et 1) qui détermine l'importance des récompenses futures par rapport aux récompenses immédiates.
• P(s′∣s,a) La probabilité de passer de l'état sss à l'état s′ en effectuant l'action a.
• max⁡a​: L'action optimale qui maximise la valeur attendue des récompenses futures.

Cette somme multiplie la valeur de chaque état suivant possible par la probabilité d'atteindre cet état, ce qui permet de saisir les récompenses futures attendues.

Équation de Bellman vs. Équation d'optimalité de Bellman

L'équation de Bellman calcule la valeur d'un état sur la base des récompenses découlant des actions entreprises et de la valeur attendue des états futurs. C'est un élément clé de l'évaluation de la qualité d'une politique lorsqu'un agent la suit dans un environnement. L'équation prend en compte toutes les actions et tous les résultats possibles et permet de déterminer la valeur d'un état donné.

En revanche, l'équation d'optimalité de Bellman est utilisée lorsque l'objectif est de trouver la meilleure politique ou la politique "optimale". 

Au lieu de se contenter d'évaluer la valeur d'un état sur la base d'une politique spécifique, il trouve la valeur maximale réalisable en considérant toutes les actions et politiques possibles. L'équation d'optimalité de Bellman y parvient en prenant la récompense maximale attendue pour toutes les actions disponibles dans chaque état. Il nous indique ainsi la valeur la plus élevée possible que nous pouvons obtenir de chaque État si nous agissons de la meilleure façon possible.

En d'autres termes, la principale différence entre les deux équations est leur orientation.

L'équation de Bellman standard évalue l'efficacité d'une politique en estimant la valeur attendue de son application. D'autre part, l'équation d'optimalité de Bellman vise à trouver la meilleure politique globale en identifiant l'action qui donne la récompense maximale à long terme dans chaque état. 

TLDR : L'équation de Bellman standard est utilisée pour l'évaluation des politiques, tandis que l'équation d'optimalité est utilisée pour l'amélioration et le contrôle des politiques.

L'équation d'optimalité de Bellman est essentielle pour résoudre les problèmes de contrôle, où l'objectif est de choisir la meilleure séquence d'actions pour maximiser les récompenses. Dans ces problèmes, les agents doivent prendre des décisions qui maximisent les récompenses immédiates et tiennent compte des récompenses futures. 

L'équation d'optimalité permet d'évaluer et de choisir systématiquement les actions qui conduisent à la récompense la plus élevée possible à long terme, ce qui permet de trouver la politique optimale. Il s'agit d'un élément central d'algorithmes tels que l'apprentissage Q et l'itération de valeur, qui sont utilisés dans l'apprentissage par renforcement pour entraîner les agents à agir de la meilleure façon possible.

Équation de Bellman dans l'apprentissage par renforcement

L'équation de Bellman est un élément essentiel de l'apprentissage par renforcement. Il aide les agents à apprendre à prendre les meilleures décisions en décomposant les tâches complexes en petites étapes.

L'équation de Bellman permet aux agents de calculer la valeur des différents états et actions, ce qui les guide dans le choix du meilleur chemin pour maximiser les récompenses. 

Ainsi, dans l'apprentissage par renforcement, l'équation de Bellman est utilisée pour évaluer et améliorer les politiques, en veillant à ce que les agents prennent de meilleures décisions au fur et à mesure qu'ils acquièrent de l'expérience.

Rôle dans le Q-Learning

L'apprentissage Q est un algorithme d'apprentissage par renforcement très répandu. L'algorithme s'appuie sur l'équation de Bellman pour estimer la valeur des paires état-action, connues sous le nom de valeurs Q. Ces valeurs indiquent à l'agent à quel point il sera gratifiant d'entreprendre une certaine action dans un état donné et de suivre la meilleure politique par la suite. 

L'équation d'optimalité de Bellman pour l'apprentissage Q trouve la valeur maximale attendue pour chaque action, aidant les agents à identifier les meilleurs mouvements pour maximiser leurs récompenses à long terme.

Par exemple, dans un problème d'apprentissage par renforcement épisodique, imaginez un agent naviguant dans un monde quadrillé. Lorsqu'il atteint un état, l'agent met à jour sa valeur Q pour cette paire état-action à l'aide de l'équation :

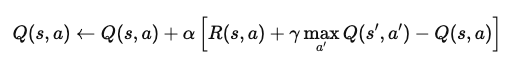
Où ?

• Q(s,a): La valeur Q de l'action a dans l'état s.
• α: Le taux d'apprentissage, qui détermine dans quelle mesure les nouvelles informations remplacent l'ancienne valeur Q.
• R(s,a): La récompense immédiate reçue après l'action a dans l'état s.
• γ : Le facteur d'actualisation, qui pondère les récompenses futures par rapport aux récompenses immédiates.
• maxa′Q(s′,a′): La valeur Q maximale pour l'état suivant s′, parmi toutes les actions possibles a′.

Cette équation met à jour la valeur Q sur la base de la récompense immédiate et de la récompense future maximale attendue. Grâce à une application répétée, l'agent apprend à se rapprocher des valeurs Q optimales et peut déterminer les meilleures actions pour maximiser les récompenses à long terme.

Équation de Bellman pour l'évaluation des politiques

L'équation de Bellman est également utilisée pour évaluer les politiques en estimant les fonctions de valeur. Dans ce contexte, il calcule la récompense attendue à long terme lorsqu'un agent suit une politique donnée à partir d'un état spécifique. Cela permet de déterminer l'efficacité d'une politique en indiquant la récompense moyenne à laquelle l'agent peut s'attendre.

L'algorithme d'itération des politiques utilise cette évaluation pour améliorer les politiques. Il commence par estimer la fonction de valeur d'une politique, puis met à jour la politique pour choisir de meilleures actions sur la base de cette valeur. Ce processus se répète jusqu'à ce que la politique converge vers la politique optimale. 

Dérivation de l'équation de Bellman

Dans cette section, nous allons décomposer l'équation de Bellman étape par étape, en commençant par les premiers principes. Nous étudierons ensuite comment les récompenses et les transitions construisent des fonctions de valeur, guidant les agents dans le choix des meilleures actions.

Dérivation étape par étape

Pour dériver l'équation de Bellman, nous commençons par le concept de fonction de valeur. La fonction de valeur, V(s)V(s)V(s), donne la récompense cumulative attendue pour commencer dans un état sss et suivre une politique optimale par la suite. Cette équation est récursive, c'est-à-dire qu'elle relie la valeur d'un état à la valeur des états suivants.

1. Définir la fonction de valeur

La fonction de valeur V(s) représente la récompense totale attendue qu'un agent recevra en commençant dans l'état sss et en suivant la politique optimale. Mathématiquement, elle peut être exprimée comme suit :

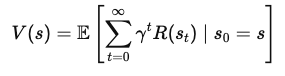
Où ?

• s est l'état actuel,
• γ est le facteur d'actualisation (entre 0 et 1), qui contrôle l'importance des récompenses futures,
• R(st) est la récompense reçue à chaque pas de temps t.

2. Ventiler les récompenses futures

Pour exprimer V(s) en termes de récompenses immédiates et de valeur des états futurs, nous séparons la première récompense de la somme de toutes les récompenses futures :

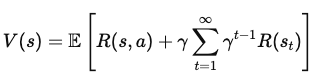
Où ?

• R(s, a) est la récompense immédiate obtenue en effectuant l'action a dans l'état s,
• γ Σ (γ(t1)) R(st) représente la somme actualisée des récompenses futures.

3. Incorporer la valeur de l'état suivant

Nous ajoutons maintenant la valeur de l'état suivant, s', que l'agent atteint après avoir effectué l'action a dans l'état s. Cela conduit à l'équation suivante :

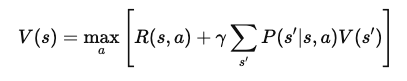
Où ?

• P(s' | s, a) est la probabilité de passer à l'état s' à partir de l'état s après avoir effectué une action a,
• maxa représente le choix de l'action a qui maximise la récompense attendue.

4. L'équation finale de Bellman

Après simplification, l'équation de Bellman pour la fonction de valeur est la suivante V(s) devient :

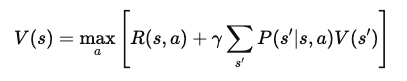
Cette forme finale de l'équation de Bellman décompose la valeur d'un état en deux composantes : la récompense immédiate et la valeur attendue de l'état suivant. Cette structure récursive permet aux algorithmes de calculer ou d'approximer V(s) de manière itérative, ce qui permet de trouver des politiques optimales au fil du temps.

Exemples et applications

Prenons un exemple avec une grille simple :

Imaginez un agent qui tente d'atteindre un objectif sur une grille en évitant les obstacles. L'agent se déplace vers le haut, le bas, la gauche ou la droite et reçoit des récompenses pour chaque mouvement. S'il atteint l'objectif, il reçoit une récompense plus élevée. En utilisant l'équation de Bellman, nous pouvons calculer la valeur de chaque état de la grille en évaluant les récompenses immédiates et les valeurs des états futurs.

Pour processus de décision de Markov (MDP), l'équation de Bellman permet de trouver la politique optimale. Si nous avons un petit PDM, comme un problème de livraison où un agent doit choisir l'itinéraire le plus rapide, nous appliquons l'équation à chaque paire état-action. Ce faisant, nous pouvons calculer les meilleures actions qui maximisent la récompense totale attendue. 

Sujets avancés : L'équation de Bellman dans le Q-Learning

Dans cette section, nous examinons comment l'équation de Bellman est appliquée dans des méthodes avancées telles que :

• Itération des valeurs
• Apprentissage par différence temporelle. 

Ces techniques aident les agents à apprendre les actions optimales en mettant à jour les estimations de valeur, même dans des environnements complexes. La compréhension de ces sujets avancés est essentielle pour maîtriser l'apprentissage par renforcement.

Itération des valeurs

L'itération des valeurs est une méthode qui utilise l'équation de Bellman pour mettre à jour les fonctions de valeur de manière itérative. L'objectif est de trouver la valeur optimale pour chaque état afin que l'agent puisse déterminer les meilleures actions. 

Dans l'itération de la valeur, l'agent met à jour la valeur de chaque état en fonction des états futurs possibles et de leurs récompenses. Ce processus se répète jusqu'à ce que les valeurs convergent vers une solution stable. Les propriétés de convergence de l'itération de la valeur garantissent que, si l'on dispose de suffisamment de temps, la politique optimale sera trouvée.

Apprentissage par différence temporelle

L'apprentissage par TD est une autre approche qui utilise l'équation de Bellman, mais qui s'en distingue par un point essentiel : elle ne nécessite pas de modèle de l'environnement. 

Au lieu de cela, il met à jour les estimations de valeur sur la base des expériences réelles que l'agent recueille. Il est donc plus pratique lorsque l'environnement est inconnu. L'apprentissage par TD comble le fossé entre les méthodes de Monte Carlo, qui s'appuient sur des épisodes complets, et la programmation dynamique, qui nécessite un modèle complet.

Applications et cas d'utilisation

L'équation de Bellman a un large éventail d'applications au-delà des modèles théoriques. Elle joue un rôle crucial dans les scénarios du monde réel où la prise de décision et l'optimisation sont nécessaires. Cette section explore la manière dont l'équation de Bellman prend en charge ces applications.

Apprentissage par renforcement dans les jeux

Dans les environnements de jeu classiques comme Atari, l'équation de Bellman permet d'optimiser les actions d'un agent afin d'obtenir le score le plus élevé. L'équation guide l'agent dans le choix des meilleures actions en évaluant les récompenses attendues pour chaque action. 

Parmi les exemples concrets, citons l'utilisation d'algorithmes d'apprentissage par renforcement profond, tels que les réseaux Q profonds (DQN), qui utilisent l'équation de Bellman pour améliorer l'intelligence artificielle des jeux. Ces méthodes ont été utilisées pour former des agents qui surpassent les joueurs humains dans divers jeux, démontrant ainsi la puissance de l'apprentissage par renforcement.

Robotique et navigation

En robotique, l'équation de Bellman aide les machines à prendre des décisions en matière de mouvement et de navigation. Les robots l'utilisent pour évaluer différents chemins et choisir celui qui maximise les récompenses futures, par exemple en atteignant un objectif dans le temps le plus court ou en consommant le moins d'énergie. 

En d'autres termes, les robots utilisent l'équation de Bellman pour prédire les résultats en fonction de leur état actuel et planifier leurs prochaines actions en conséquence. Ce processus de prise de décision est essentiel pour naviguer dans un labyrinthe ou éviter les obstacles dans des environnements dynamiques.

Conclusion

L'équation de Bellman est fondamentale pour le développement de systèmes intelligents, en particulier pour l'apprentissage par renforcement et d'autres domaines de l'intelligence artificielle. Elle sert de base aux algorithmes qui permettent aux systèmes d'apprendre, de s'adapter et d'optimiser leurs actions dans des environnements dynamiques, ce qui conduit à une résolution plus efficace des problèmes dans des environnements incertains. 

Voici quelques ressources pour poursuivre votre apprentissage : 

• Apprentissage par renforcement avec Gymnasium en Python 
• Apprentissage par renforcement : Une introduction avec des exemples en Python
• Algorithme d'apprentissage par renforcement SARSA en Python : Un guide complet
• Qu'est-ce que l'apprentissage par renforcement à partir du feedback humain ? 
• RLAIF : Qu'est-ce que l'apprentissage par renforcement à partir du retour d'expérience de l'IA ?