Die Bellman-Gleichung beim Reinforcement Learning verstehen

In den frühen 1950er Jahren machte sich Richard Bellman, ein visionärer Mathematiker und Informatiker, auf den Weg, um die Komplexität der Entscheidungsfindung in unsicheren Umgebungen zu entschlüsseln. Angetrieben von der Notwendigkeit effizienter Problemlösungsmethoden führte er das revolutionäre Konzept der dynamischen Programmierung ein, das komplizierte Probleme in handhabbare Teilprobleme zerlegt. 

Als er diesen Ansatz erforschte, formulierte Bellman die später so genannte Bellman-Gleichung: Ein mathematischer Ausdruck, der den Wert einer Entscheidung in einem bestimmten Zustand auf der Grundlage der möglichen zukünftigen Zustände und der damit verbundenen Belohnungen bewertet. Seine bahnbrechende Arbeit gipfelte in der Veröffentlichung seines Buches Dynamic Programming aus dem Jahr 1957, das die theoretische Grundlage für die Optimierungs- und Kontrolltheorie legte und gleichzeitig den Weg für Fortschritte in der künstlichen Intelligenz und im Verstärkungslernen.

Bis heute prägen Bellmans Ideen die Art und Weise, wie Maschinen lernen und sich an ihre Umgebung anpassen, und haben ein bleibendes Vermächtnis in der Mathematik und Informatik hinterlassen. Beim Verstärkungslernen ist die Bellman-Gleichung entscheidend, um zu verstehen, wie Agenten mit ihrer Umgebung interagieren, was sie für die Lösung verschiedener Probleme in Markov-Entscheidungsprozessen (MDPs) unerlässlich macht. 

In diesem Artikel erfahren wir, was die Gleichung ist, wie sie sich von der Bellman-Optimalitätsgleichung unterscheidet, wie sie beim Reinforcement Learning eingesetzt wird und vieles mehr.

Was ist die Bellman-Gleichung?

Die Bellman-Gleichung ist eine rekursive Formel, die bei der Entscheidungsfindung und beim Verstärkungslernen verwendet wird. Sie zeigt, wie der Wert eines bestimmten Zustands von den erhaltenen Belohnungen und dem Wert zukünftiger Zustände abhängt. 

Vereinfacht ausgedrückt, zerlegt die Bellman-Gleichung ein komplexes Problem in kleinere Schritte, wodurch es leichter zu lösen ist. Die Gleichung hilft dabei, den besten Weg für Entscheidungen zu finden, wenn das Ergebnis von einer Reihe von Aktionen abhängt.

Mathematisch lässt sich die Bellman-Gleichung wie folgt formulieren:

Wo:

• V(s): Der Wert des Zustands sss, der die langfristige Belohnung dafür darstellt, in diesem Zustand zu sein.
• R(s,a): Die unmittelbare Belohnung für die Aktion aaa im Staat sss.
• γ: Der Diskontierungsfaktor (zwischen 0 und 1), der die Bedeutung zukünftiger Belohnungen im Vergleich zu sofortigen Belohnungen bestimmt.
• P(s′∣s,a) Die Wahrscheinlichkeit, vom Zustand sss in den Zustand s′ überzugehen, indem man die Aktion a.
• max⁡a​: Die optimale Handlung, die den Erwartungswert der zukünftigen Belohnungen maximiert.

Diese Summe multipliziert den Wert jedes möglichen nächsten Zustands mit der Wahrscheinlichkeit, diesen Zustand zu erreichen, und erfasst somit die erwarteten zukünftigen Belohnungen.

Bellman-Gleichung vs. Bellmansche Optimalitätsgleichung

Die Bellman-Gleichung berechnet den Wert eines Zustands auf der Grundlage der Belohnungen für Handlungen und des erwarteten Werts zukünftiger Zustände. Sie ist ein wichtiger Teil der Bewertung, wie gut eine Richtlinie ist, wenn ein Agent sie in einer Umgebung befolgt. Die Gleichung betrachtet alle möglichen Aktionen und Ergebnisse und hilft dabei, den Wert eines bestimmten Zustands zu bestimmen.

Im Gegensatz dazu wird die Bellman-Optimalitätsgleichung verwendet, wenn das Ziel darin besteht, die beste oder "optimale" Strategie zu finden. 

Anstatt nur den Wert eines Zustands auf der Grundlage einer bestimmten Politik zu bewerten, findet es den maximal erreichbaren Wert unter Berücksichtigung aller möglichen Aktionen und Politiken. Die Bellmansche Optimalitätsgleichung tut dies, indem sie die maximale erwartete Belohnung über alle in jedem Zustand verfügbaren Aktionen ermittelt. Auf diese Weise erfahren wir den höchstmöglichen Wert, den wir von jedem Staat erhalten können, wenn wir uns bestmöglich verhalten.

Mit anderen Worten: Der Hauptunterschied zwischen den beiden Gleichungen ist ihr Fokus.

Die Standard-Bellman-Gleichung bewertet die Effektivität einer Strategie, indem sie den Erwartungswert der Befolgung dieser Strategie schätzt. Auf der anderen Seite zielt die Bellman-Optimalitätsgleichung darauf ab, die insgesamt beste Strategie zu finden, indem die Aktion ermittelt wird, die in jedem Zustand die maximale langfristige Belohnung bringt. 

TLDR: Die Standard-Bellman-Gleichung wird für die Bewertung der Politik verwendet, während die Optimalitätsgleichung für die Verbesserung und Kontrolle der Politik genutzt wird.

Die Bellman-Optimalitätsgleichung ist wichtig für die Lösung von Steuerungsproblemen, bei denen das Ziel darin besteht, die beste Abfolge von Handlungen zu wählen, um die Belohnung zu maximieren. Bei diesen Problemen müssen die Agenten Entscheidungen treffen, die den unmittelbaren Gewinn maximieren und zukünftige Gewinne berücksichtigen. 

Die Optimalitätsgleichung ermöglicht eine systematische Bewertung und Auswahl von Handlungen, die zur höchstmöglichen langfristigen Belohnung führen, und hilft so, die optimale Politik zu finden. Sie ist ein zentraler Bestandteil von Algorithmen wie Q-learning und Value Iteration, die beim Reinforcement Learning eingesetzt werden, um Agenten so zu trainieren, dass sie auf die bestmögliche Weise handeln.

Bellman-Gleichung beim Verstärkungslernen

Die Bellman-Gleichung ist ein zentraler Bestandteil des Verstärkungslernens. Es hilft den Agenten zu lernen, wie sie die besten Entscheidungen treffen können, indem sie komplexe Aufgaben in kleinere Schritte zerlegen.

Die Bellman-Gleichung ermöglicht es den Agenten, den Wert verschiedener Zustände und Aktionen zu berechnen und so den besten Weg zur Maximierung der Belohnung zu wählen. 

Beim Reinforcement Learning wird die Bellman-Gleichung verwendet, um Strategien zu bewerten und zu verbessern, damit die Agenten mit zunehmender Erfahrung bessere Entscheidungen treffen.

Rolle beim Q-Learning

Q-Learning ist ein beliebter Algorithmus zum Verstärkungslernen. Der Algorithmus nutzt die Bellman-Gleichung, um den Wert von Zustands-Aktions-Paaren, den sogenannten Q-Werten, zu schätzen. Diese Werte sagen dem Agenten, wie lohnend es ist, in einem bestimmten Zustand eine bestimmte Aktion durchzuführen und danach die beste Strategie zu verfolgen. 

Die Bellman-Optimalitätsgleichung für Q-Learning findet den maximalen Erwartungswert für jede Aktion und hilft den Agenten, die besten Züge zu finden, um ihren langfristigen Gewinn zu maximieren.

Stell dir zum Beispiel ein episodisches Verstärkungslernproblem vor, bei dem ein Agent durch eine Gitterwelt navigiert. Wenn er einen Zustand erreicht, aktualisiert der Agent seinen Q-Wert für dieses Zustands-Aktionspaar anhand der Gleichung:

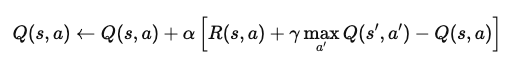
Wo:

• Q(s,a): Der Q-Wert für das Ausführen der Aktion a im Zustand s.
• α: Die Lernrate, die bestimmt, wie sehr neue Informationen den alten Q-Wert überlagern.
• R(s,a): Die unmittelbare Belohnung, die du nach einer Aktion a im Zustand s erhältst.
• γ: Der Abzinsungsfaktor, der künftige Belohnungen im Vergleich zu sofortigen Belohnungen abwägt.
• max⁡a′Q(s′,a′): Der maximale Q-Wert für den nächsten Zustand s′, über alle möglichen Aktionen a′.

Diese Gleichung aktualisiert den Q-Wert auf der Grundlage der sofortigen Belohnung und der maximalen erwarteten zukünftigen Belohnungen. Durch wiederholte Anwendung lernt der Agent, sich den optimalen Q-Werten anzunähern, und kann die besten Aktionen zur Maximierung der langfristigen Belohnung bestimmen.

Bellman-Gleichung für die Politikbewertung

Die Bellman-Gleichung wird auch zur Bewertung von Maßnahmen durch Schätzung von Wertfunktionen verwendet. In diesem Zusammenhang wird die erwartete langfristige Belohnung berechnet, wenn ein Agent ab einem bestimmten Zustand eine bestimmte Politik verfolgt. Dies hilft bei der Bestimmung, wie effektiv eine Politik ist, indem es die durchschnittliche Belohnung anzeigt, die der Agent erwarten kann.

Der Iterationsalgorithmus für die Richtlinien nutzt diese Bewertung, um die Richtlinien zu verbessern. Es beginnt mit der Schätzung der Wertfunktion für eine Politik und aktualisiert dann die Politik, um auf der Grundlage dieses Wertes bessere Aktionen zu wählen. Dieser Prozess wird so lange wiederholt, bis die Politik zum Optimum konvergiert und keine weiteren Verbesserungen mehr vorgenommen werden können. 

Ableitung der Bellman-Gleichung

In diesem Abschnitt werden wir die Bellman-Gleichung Schritt für Schritt aufschlüsseln und mit den ersten Prinzipien beginnen. Dann werden wir untersuchen, wie Belohnungen und Übergänge Wertfunktionen bilden, die die Agenten bei der Wahl der besten Aktionen leiten.

Schritt-für-Schritt-Ableitung

Um die Bellman-Gleichung abzuleiten, beginnen wir mit dem Konzept der Wertfunktion. Die Wertfunktion, V(s)V(s)V(s), gibt die erwartete kumulative Belohnung für den Start in einem Zustand sss und das Befolgen einer optimalen Politik danach an. Diese Gleichung ist rekursiv, das heißt, sie setzt den Wert eines Zustands mit dem Wert der nachfolgenden Zustände in Beziehung.

1. Definiere die Wertfunktion

Die Wertfunktion V(s) stellt die gesamte erwartete Belohnung dar, die ein Agent erhält, wenn er im Zustand sss startet und die optimale Strategie verfolgt. Mathematisch lässt sich das wie folgt ausdrücken:

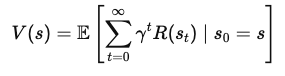
Wo:

• s ist der aktuelle Zustand,
• γ ist der Diskontierungsfaktor (zwischen 0 und 1), der die Bedeutung zukünftiger Belohnungen steuert,
• R(st) ist die in jedem Zeitschritt erhaltene Belohnung t.

2. Zukünftige Belohnungen aufschlüsseln

Zum Ausdruck bringen V(s) in Form von unmittelbaren Belohnungen und dem Wert zukünftiger Zustände auszudrücken, trennen wir die erste Belohnung von der Summe aller zukünftigen Belohnungen:

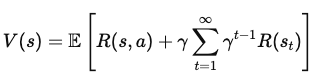
Wo:

• R(s, a) ist die unmittelbare Belohnung für das Ausführen der Handlung a im Zustand s,
• γ Σ (γ(t1)) R(st) steht für die abgezinste Summe der zukünftigen Belohnungen.

3. Den nächsten Zustandswert einbeziehen

Nun fügen wir den Wert des nächsten Zustands s'hinzu, den der Agent erreicht, nachdem er die Aktion a im Zustand s ausgeführt hat . Daraus ergibt sich die Gleichung:

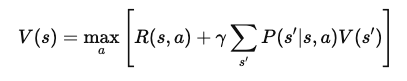
Wo:

• P(s' | s, a) ist die Wahrscheinlichkeit des Übergangs in den Zustand s' von Zustand s nach der Ausführung der Aktion a,
• maxa steht für die Wahl der Aktion a die die erwartete Belohnung maximiert.

4. Die endgültige Bellman-Gleichung

Nach der Vereinfachung ergibt sich die Bellman-Gleichung für die Wertfunktion V(s) wird:

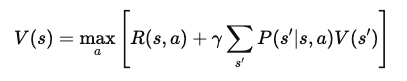
Bei dieser endgültigen Form der Bellman-Gleichung wird der Wert eines Zustands in zwei Komponenten zerlegt: die unmittelbare Belohnung und der erwartete Wert des nächsten Zustands. Diese rekursive Struktur ermöglicht es den Algorithmen, V(s) iterativ zu berechnen oder zu approximieren, was dabei hilft, im Laufe der Zeit optimale Strategien zu finden.

Beispiele und Anwendungen

Lass uns ein Beispiel mit einer einfachen Gitterwelt durchgehen:

Stell dir einen Agenten vor, der versucht, ein Ziel auf einem Gitter zu erreichen und dabei Hindernissen auszuweichen. Der Agent bewegt sich nach oben, unten, links oder rechts und erhält für jede Bewegung eine Belohnung. Wenn er das Ziel erreicht, bekommt er eine höhere Belohnung. Mithilfe der Bellman-Gleichung können wir den Wert für jeden Zustand auf dem Raster berechnen, indem wir die unmittelbaren Belohnungen und die zukünftigen Zustandswerte auswerten.

Für Markov-Entscheidungsprozesse (MDPs) hilft die Bellman-Gleichung, die optimale Strategie zu finden. Wenn wir ein kleines MDP haben, z. B. ein Lieferproblem, bei dem ein Agent die schnellste Route wählen muss, wenden wir die Gleichung auf jedes Zustands-Aktionspaar an. Auf diese Weise können wir die besten Aktionen berechnen, die den erwarteten Gesamtgewinn maximieren. 

Fortgeschrittene Themen: Bellman-Gleichung im Q-Learning

In diesem Abschnitt untersuchen wir, wie die Bellman-Gleichung in fortgeschrittenen Methoden wie

• Wert-Iteration
• Lernen mit Zeitdifferenz. 

Diese Techniken helfen den Agenten dabei, optimale Handlungen zu erlernen, indem sie Wertschätzungen aktualisieren, selbst in komplexen Umgebungen. Das Verständnis dieser fortgeschrittenen Themen ist der Schlüssel zur Beherrschung des Reinforcement Learning.

Wert-Iteration

Die Wertiteration ist eine Methode, die die Bellman-Gleichung nutzt, um Wertfunktionen iterativ zu aktualisieren. Das Ziel ist es, den optimalen Wert für jeden Zustand zu finden, damit der Agent die besten Aktionen bestimmen kann. 

Bei der Wert-Iteration aktualisiert der Agent den Wert jedes Zustands auf der Grundlage möglicher zukünftiger Zustände und ihrer Belohnungen. Dieser Vorgang wiederholt sich, bis die Werte zu einer stabilen Lösung konvergieren. Die Konvergenzeigenschaften der Wertiteration stellen sicher, dass sie mit genügend Zeit die optimale Strategie findet.

Lernen mit zeitlicher Differenz

TD-Lernen ist ein weiterer Ansatz, der die Bellman-Gleichung verwendet, sich aber in einem entscheidenden Punkt unterscheidet: Er benötigt kein Modell der Umgebung. 

Stattdessen aktualisiert er die Wertschätzungen auf der Grundlage der tatsächlichen Erfahrungen, die der Agent sammelt. Das macht es praktischer, wenn die Umgebung unbekannt ist. TD-Lernen schließt die Lücke zwischen Monte-Carlo-Methoden, die auf vollständigen Episoden beruhen, und dynamischer Programmierung, die ein vollständiges Modell benötigt.

Anwendungen und Anwendungsfälle

Die Bellman-Gleichung hat eine breite Palette von Anwendungen, die über theoretische Modelle hinausgehen. Sie spielt eine entscheidende Rolle in realen Szenarien, in denen Entscheidungen getroffen und Optimierungen vorgenommen werden müssen. In diesem Abschnitt wird untersucht, wie die Bellman-Gleichung diese Anwendungen unterstützt.

Verstärkungslernen in Spielen

In klassischen Spielumgebungen wie Atari hilft die Bellman-Gleichung dabei, die Aktionen eines Agenten zu optimieren, um die höchste Punktzahl zu erreichen. Die Gleichung leitet den Agenten bei der Auswahl der besten Züge an, indem er die erwarteten Belohnungen für jede Aktion abwägt. 

Zu den Beispielen aus der Praxis gehört der Einsatz von Deep Reinforcement Learning-Algorithmen, wie Deep Q-Networks (DQNs), die die Bellman-Gleichung nutzen, um die Spiele-KI zu verbessern. Diese Methoden wurden verwendet, um Agenten zu trainieren, die menschliche Spieler in verschiedenen Spielen übertreffen, was die Stärke des Verstärkungslernens zeigt.

Robotik und Navigation

In der Robotik hilft die Bellman-Gleichung Maschinen, Entscheidungen über Bewegung und Navigation zu treffen. Roboter nutzen sie, um verschiedene Wege zu bewerten und denjenigen zu wählen, der den zukünftigen Nutzen maximiert, z.B. ein Ziel in der kürzesten Zeit oder mit der geringsten Energie zu erreichen. 

Mit anderen Worten: Roboter nutzen die Bellman-Gleichung, um auf der Grundlage ihres aktuellen Zustands Ergebnisse vorherzusagen und ihre nächsten Schritte entsprechend zu planen. Dieser Entscheidungsprozess ist entscheidend, um durch ein Labyrinth zu navigieren oder Hindernissen in dynamischen Umgebungen auszuweichen.

Fazit

Die Bellman-Gleichung ist von grundlegender Bedeutung für die Entwicklung intelligenter Systeme - insbesondere für das Reinforcement Learning und andere Bereiche der künstlichen Intelligenz. Sie dient als Grundlage für Algorithmen, die es Systemen ermöglichen, in dynamischen Umgebungen zu lernen, sich anzupassen und ihre Handlungen zu optimieren, was zu einer effizienteren und effektiveren Problemlösung in unsicheren Umgebungen führt. 

Hier findest du einige Ressourcen, um dich weiterzubilden: 

• Reinforcement Learning mit Gymnasium in Python 
• Reinforcement Learning: Eine Einführung mit Python-Beispielen
• SARSA Reinforcement Learning Algorithmus in Python: Ein vollständiger Leitfaden
• Was ist Reinforcement Learning aus menschlichem Feedback? 
• RLAIF: Was ist Reinforcement Learning aus KI-Feedback?