Understanding the Bellman Equation in Reinforcement Learning

In the early 1950s, Richard Bellman, a visionary mathematician and computer scientist, embarked on a journey to unravel the complexities of decision-making in uncertain environments. Driven by the need for efficient problem-solving methods, he introduced the revolutionary concept of dynamic programming, which breaks down intricate problems into manageable subproblems. 

As he explored this approach, Bellman formulated what would later be known as the Bellman Equation: a mathematical expression that evaluates the value of a decision in a given state based on the potential future states and their associated rewards. His groundbreaking work culminated in the publication of his 1957 book, Dynamic Programming, which laid the theoretical foundation for optimization and control theory while paving the way for advancements in artificial intelligence and reinforcement learning.

Today, Bellman's ideas continue to shape how machines learn and adapt to their environments, leaving a lasting legacy in mathematics and computer science. In reinforcement learning, the Bellman Equation is crucial in understanding how agents interact with their surroundings, making it essential for solving various problems in Markov Decision Processes (MDPs). 

In this article, we will explore what the equation is, how it compares to the Bellman Optimality Equation, how it’s used in reinforcement learning, and more.

What is the Bellman Equation?

The Bellman Equation is a recursive formula used in decision-making and reinforcement learning. It shows how the value of being in a certain state depends on the rewards received and the value of future states. 

In simple terms, the Bellman Equation breaks down a complex problem into smaller steps, making it easier to solve. The equation helps find the best way to make decisions when outcomes depend on a series of actions.

Mathematically, the Bellman Equation is written as:

Where:

• V(s): The value of state sss, which represents the long-term reward of being in that state.
• R(s,a): The immediate reward received for taking action aaa in state sss.
• γ: The discount factor (between 0 and 1) that determines the importance of future rewards compared to immediate rewards.
• P(s′∣s,a) The probability of transitioning to state s′ from state sss by taking action a.
• max⁡a​: The optimal action that maximizes the expected value of future rewards.

This sum multiplies the value of each possible next state by the probability of reaching that state, effectively capturing the expected future rewards.

Bellman Equation vs. Bellman Optimality Equation

The Bellman Equation calculates the value of a state based on the rewards from taking actions and the expected value of future states. It’s a key part of evaluating how good a policy is when an agent follows it in an environment. The equation looks at all the possible actions and outcomes and helps determine the value of being in a certain state.

In contrast, the Bellman Optimality Equation is used when the goal is to find the best or "optimal" policy. 

Instead of just evaluating the value of a state based on a specific policy, it finds the maximum value achievable by considering all possible actions and policies. Bellman Optimality Equation does this by taking the maximum expected reward over all actions available in each state. This way, it tells us the highest possible value we can get from each state if we act in the best way possible.

In other words, the main difference between the two equations is their focus.

The standard Bellman Equation evaluates the effectiveness of a policy by estimating the expected value of following it. On the other hand, the Bellman Optimality Equation aims to find the best policy overall by identifying the action that gives the maximum long-term reward in each state. 

TLDR: The standard Bellman Equation is used for policy evaluation, while the optimality equation is used for policy improvement and control.

The Bellman Optimality Equation is essential for solving control problems, where the objective is to choose the best sequence of actions to maximize rewards. In these problems, agents must make decisions that maximize immediate rewards and consider future rewards. 

The optimality equation provides a way to systematically evaluate and choose actions that lead to the highest possible long-term reward, helping to find the optimal policy. It is a central part of algorithms like Q-learning and value iteration, which are used in reinforcement learning to train agents to act in the best way possible.

Bellman Equation in Reinforcement Learning

The Bellman Equation is a core part of reinforcement learning. It helps agents learn how to make the best decisions by breaking down complex tasks into smaller steps.

Namely, the Bellman Equation enables agents to calculate the value of different states and actions, which guides them in choosing the best path to maximize rewards. 

Thus, In reinforcement learning, the Bellman Equation is used to evaluate and improve policies, ensuring agents make better decisions as they gain experience.

Role in Q-Learning

Q-learning is a popular reinforcement learning algorithm. The algorithm leverages the Bellman Equation to estimate the value of state-action pairs, known as Q-values. These values tell the agent how rewarding it will be to take a certain action in a given state and follow the best policy afterward. 

The Bellman Optimality Equation for Q-learning finds the maximum expected value for each action, helping agents identify the best moves to maximize their long-term rewards.

For example, in an episodic reinforcement learning problem, imagine an agent navigating a grid world. When it reaches a state, the agent updates its Q-value for that state-action pair using the equation:

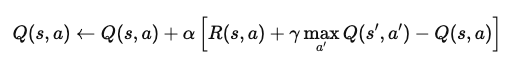
Where:

• Q(s,a): The Q-value for taking action a in state s.
• α: The learning rate, which determines how much new information overrides the old Q-value.
• R(s,a): The immediate reward received after taking action a in state s.
• γ: The discount factor, which weighs future rewards relative to immediate rewards.
• max⁡a′Q(s′,a′): The maximum Q-value for the next state s′, across all possible actions a′.

This equation updates the Q-value based on the immediate reward and the maximum expected future rewards. Through repeated application, the agent learns to approximate the optimal Q-values and can determine the best actions to maximize long-term rewards.

Bellman Equation for policy evaluation

The Bellman Equation is also used to evaluate policies by estimating value functions. In this context, it calculates the expected long-term reward when an agent follows a given policy from a specific state. This helps determine how effective a policy is by showing the average reward the agent can expect.

The policy iteration algorithm uses this evaluation to improve policies. It starts by estimating the value function for a policy and then updates the policy to choose better actions based on this value. This process repeats until the policy converges to the optimal one, at which point no further improvements can be made. 

Bellman Equation Derivation

In this section, we'll break down the Bellman Equation step by step, starting from the first principles. We will then explore how rewards and transitions build value functions, guiding agents in choosing the best actions.

Step-by-step derivation

To derive the Bellman Equation, we start with the concept of a value function. The value function, V(s)V(s)V(s), gives the expected cumulative reward for starting in a state sss and following an optimal policy thereafter. This equation is recursive, meaning it relates the value of a state to the value of subsequent states.

1. Define the value function

The value function V(s) represents the total expected reward an agent will receive from starting in state sss and following the optimal policy. Mathematically, it can be expressed as:

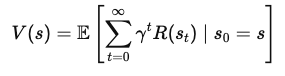
Where:

• s is the current state,
• γ is the discount factor (between 0 and 1), which controls the importance of future rewards,
• R(st) is the reward received at each time step t.

2. Breaking down future rewards

To express V(s) in terms of immediate rewards and the value of future states, we separate the first reward from the sum of all future rewards:

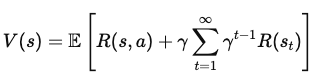
Where:

• R(s, a) is the immediate reward obtained by taking action a in state s,
• γ Σ (γ(t1)) R(st) represents the discounted sum of future rewards.

3. Incorporate the next state value

Now we add the value of the next state, s', which the agent reaches after taking action a in state s. This leads to the equation:

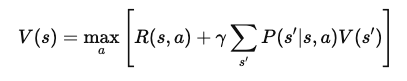
Where:

• P(s' | s, a) is the probability of transitioning to state s' from state s after taking action a,
• maxa represents the choice of the action a that maximizes the expected reward.

4. The Final Bellman Equation

After simplifying, the Bellman Equation for the value function V(s) becomes:

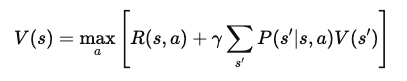
This final form of the Bellman Equation decomposes the value of a state into two components: the immediate reward and the expected value of the next state. This recursive structure allows algorithms to compute or approximate V(s) iteratively, which helps in finding optimal policies over time.

Examples and applications

Let’s walk through an example with a simple grid world:

Imagine an agent trying to reach a goal on a grid while avoiding obstacles. The agent moves up, down, left, or right and gets rewards for each move. If it reaches the goal, it gets a higher reward. Using the Bellman Equation, we can calculate the value for each state on the grid by evaluating the immediate rewards and future state values.

For Markov Decision Processes (MDPs), the Bellman Equation helps find the optimal policy. If we have a small MDP, like a delivery problem where an agent must pick the fastest route, we apply the equation to each state-action pair. By doing so, we can calculate the best actions that maximize the total expected reward. 

Advanced Topics: Bellman Equation in Q-Learning

In this section, we explore how the Bellman Equation is applied in advanced methods like:

• Value iteration
• Temporal-Difference learning. 

These techniques help agents learn optimal actions by updating value estimates, even in complex environments. Understanding these advanced topics is key to mastering reinforcement learning.

Value iteration

Value iteration is a method that uses the Bellman Equation to update value functions iteratively. The goal is to find the optimal value for each state so that the agent can determine the best actions. 

In value iteration, the agent updates each state’s value based on possible future states and their rewards. This process repeats until the values converge to a stable solution. The convergence properties of value iteration ensure that, given enough time, it will find the optimal policy.

Temporal-difference learning

TD learning is another approach that uses the Bellman Equation but differs in a key way—it doesn’t need a model of the environment. 

Instead, it updates value estimates based on actual experiences the agent gathers. This makes it more practical when the environment is unknown. TD learning bridges the gap between Monte Carlo methods, which rely on complete episodes, and dynamic programming, which needs a full model.

Applications and Use Cases

The Bellman Equation has a wide range of applications beyond theoretical models. It plays a crucial role in real-world scenarios where decision-making and optimization are needed. This section explores how the Bellman Equation supports these applications.

Reinforcement learning in games

In classic gaming environments like Atari, the Bellman Equation helps optimize an agent's actions to achieve the highest score. The equation guides the agent in selecting the best moves by evaluating the expected rewards for each action. 

Real-world examples include using deep reinforcement learning algorithms, like Deep Q-Networks (DQNs), that use the Bellman Equation to improve game AI. These methods have been used to train agents that outperform human players in various games, showing the power of reinforcement learning.

Robotics and navigation

In robotics, the Bellman Equation helps machines make decisions about movement and navigation. Robots use it to evaluate different paths and choose the one that maximizes future rewards, such as reaching a goal in the shortest time or with the least energy. 

In other words, robots use the Bellman equation to help them predict outcomes based on their current state and plan their next moves accordingly. This decision-making process is critical for navigating through a maze or avoiding obstacles in dynamic environments.

Conclusion

The Bellman Equation is fundamental in developing intelligent systems – particularly in reinforcement learning and other areas of artificial intelligence. It serves as the basis for algorithms that allow systems to learn, adapt, and optimize their actions in dynamic environments, which leads to more efficient and effective problem-solving in uncertain environments. 

Here are some resources to continue your learning: 

• Reinforcement Learning with Gymnasium in Python 
• Reinforcement Learning: An Introduction With Python Examples
• SARSA Reinforcement Learning Algorithm in Python: A Full Guide
• What is Reinforcement Learning from Human Feedback 
• RLAIF: What is Reinforcement Learning From AI Feedback?