Vectores y valores propios: Ideas clave para la ciencia de datos

Los vectores propios y los valores propios son conceptos fundamentales del álgebra lineal que tienen implicaciones de gran alcance en la ciencia de datos y el aprendizaje automático. Estas entidades matemáticas proporcionan valiosos conocimientos sobre el comportamiento de las transformaciones lineales, lo que nos permite comprender la estructura subyacente de los datos, simplificar conjuntos de datos complejos con un gran número de características y, por tanto, posibilitar su procesamiento para alcanzar el objetivo deseado.

Si esto te suena a reducción de la dimensionalidad, estás en lo cierto. Los vectores propios y los valores propios funcionan bajo el capó de muchas técnicas de reducción de la dimensionalidad, como el análisis de componentes principales (ACP). También son el engranaje de la agrupación espectral, que implica la reducción de la dimensionalidad como paso inicial.

Para dominar el concepto de mundo propio, necesitarías tener una buena comprensión de conceptos previos de álgebra lineal, principalmente vectores y escalares, transformación lineal y determinantes. Si no conoces estos conceptos, puedes seguir nuestro curso práctico de Álgebra Lineal para la Ciencia de Datos en R, o si eres usuario de Python, puedes seguir este tutorial de SciPy sobre vectores y matrices.

¿Qué son los vectores propios y los valores propios?

Empecemos por el hecho de que la parte "eigen" de los vectores y valores propios tiene realmente un significado y no es el nombre de un tipo que los inventó. Eigen es una palabra alemana que puede traducirse aproximadamente en este contexto como "lo característico" o "lo intrínseco" de algo.

Ahora, imagina que sometemos a un grupo de vectores a una transformación lineal, como una escala, un cizallamiento o una rotación. Algunos vectores cambian de dirección, y otros no. Los vectores que no cambian de sentido (o giran exactamente en sentido contrario) son los que llamamos vectores propios, ya que se convierten en los vectores "característicos" de la transformación ocurrida (o de la matriz que describen). La cantidad (magnitud) a la que se han escalado es el valor propio. Es decir, el valor propio es el factor de escala de la transformación.

Comprender los vectores y valores propios

Para comprender mejor los conceptos de ambos, vamos a trabajar con un caso geométrico y luego pasaremos a su aplicación en la ciencia de datos.

Interpretación geométrica

Imagina un espacio bidimensional, en el que tenemos tres vectores, uno azul que se apoya en el eje x, uno rojo que se apoya en el eje y, y uno verde que se apoya en diagonal entre los dos. Ahora, aplicamos una transformación de escala a lo largo del eje y con un factor de dos, como se muestra en las imágenes siguientes.

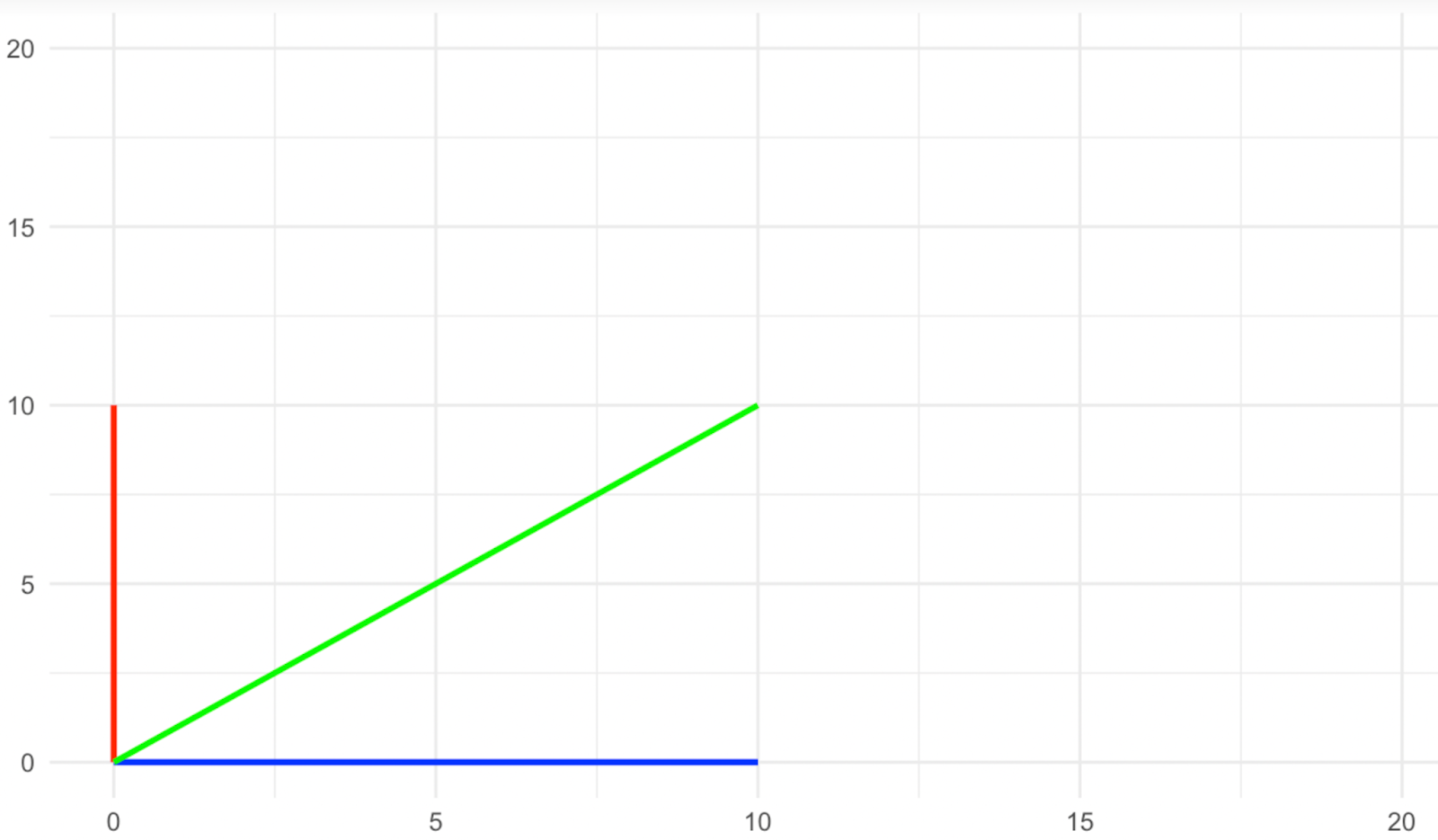
Vectores antes del estiramiento. Imagen del autor

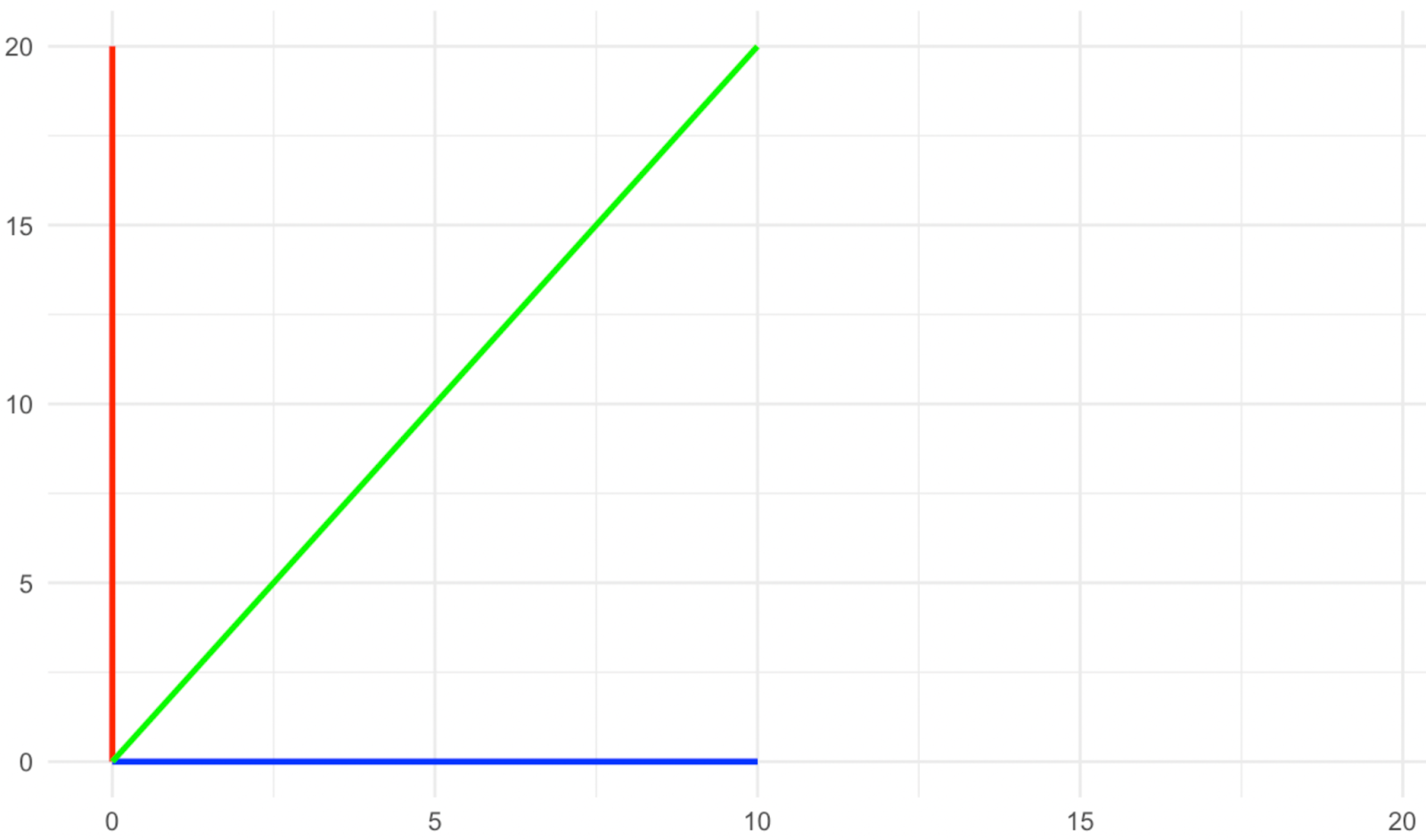
Vectores después del estiramiento. Imagen del autor

¿Qué ha pasado con los vectores de dirección? El rojo y el azul no cambiaron de dirección con la escala, mientras que el verde sí lo hizo, ¿verdad? Por tanto, en este tipo de transformación, los vectores rojo y azul son lo que llamamos vectores propios, ya que se convierten en los vectores característicos de la transformación.

Vuelve a mirar las imágenes anteriores y observa qué ha ocurrido con la magnitud de los vectores propios (los rojos y azules). El vector propio azul no cambió su magnitud, mientras que el rojo se duplicó o, en una forma elegante de decir, se escaló al factor dos. La cantidad en que cada uno de los vectores propios se escaló con la transformación es lo que llamamos valores propios. Por tanto, el valor propio del vector propio azul aquí es 1 (piensa en ello como una multiplicación), mientras que el valor propio del vector propio rojo es 2, ya que su magnitud se ha duplicado.

Propiedades de los valores propios

Considera la transformación que se muestra en las imágenes siguientes y, en primer lugar, piensa cuáles son los vectores propios en este caso. Si has dicho que son los tres vectores, el rojo, el verde y el amarillo, estás en lo cierto, ya que todos apuntan en la dirección exactamente opuesta después de la transformación. Vemos que el signo del número (el valor propio) puede darnos información adicional sobre la transformación que se ha producido. Un valor propio positivo indica que la transformación no incluyó una rotación, mientras que un valor propio negativo indica que la transformación incluyó una rotación del vector propio alrededor de su origen.

Vectores antes de la rotación. Imagen del autor

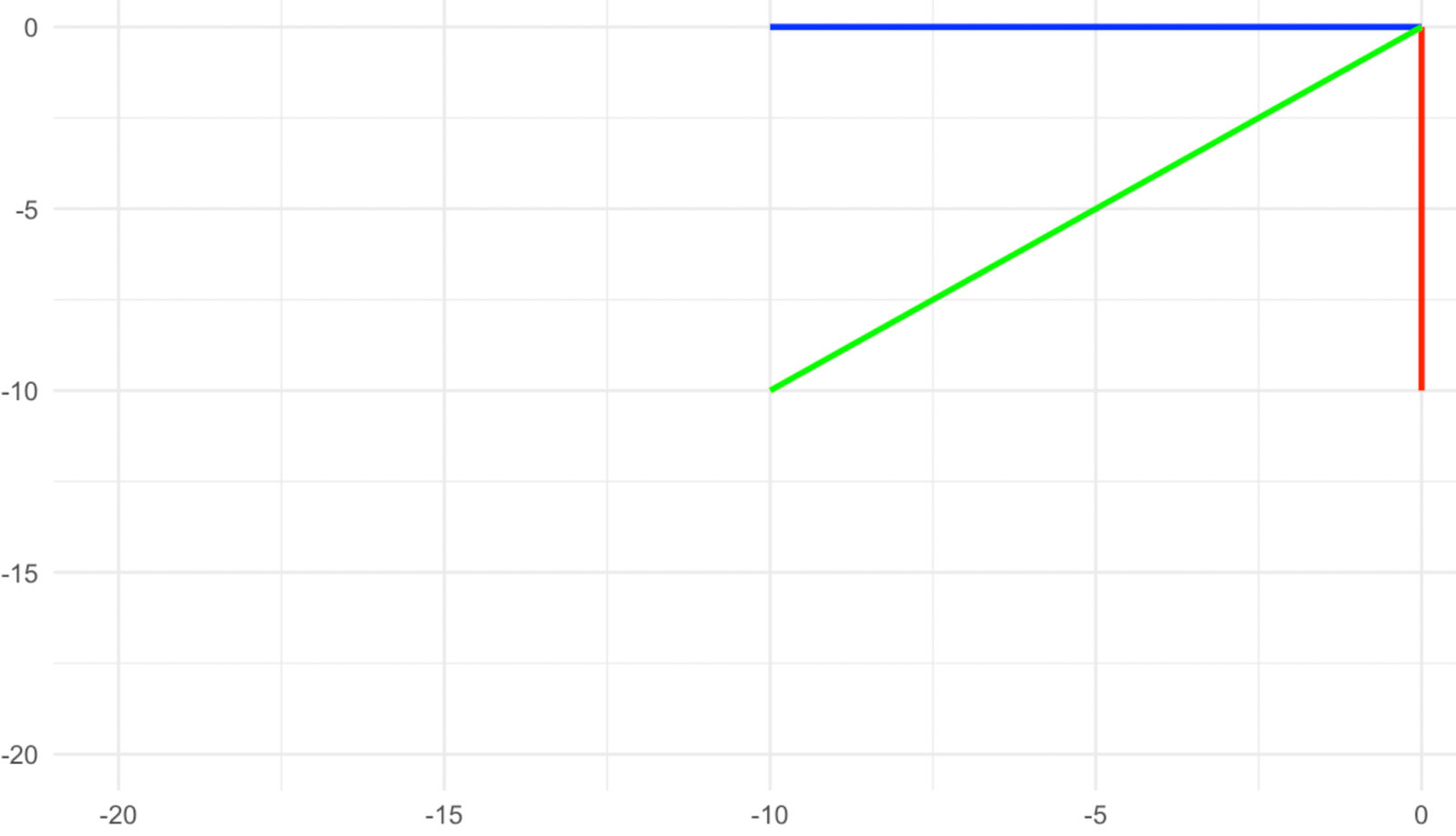
Vectores después de la rotación. Imagen del autor

Ahora, ¿cuál es el valor propio de cada uno de estos vectores propios? El hecho de que su magnitud siga siendo la misma significa que el valor propio es 1, pero el hecho de que también hayan girado significa que el signo del 1 debe ser negativo. Por tanto, el valor propio en este caso es -1.

En nuestro ejemplo, los valores propios son simples (todos son 1), pero los valores propios pueden ser cualquier número, ya sea un entero o un número entero, como 1 y 2, o un racional (fracción) como ½ y 0,75. Pueden ser lo que se llama números irracionales, como el valor de π. Los valores propios pueden ser incluso números complejos, como a + bi, donde "a" y "b" son números reales por separado e "i" es una unidad imaginaria, como la raíz cuadrada de -1. Los valores propios complejos también pueden indicar el tipo de transformación lineal que se ha producido, ya sea también una rotación o una más compleja como la oscilación.

Cómo calcular los vectores y valores propios

Aunque las bibliotecas del paquete base en R, y las bibliotecas en Python como SciPy y NumPy, pueden encontrar fácilmente los vectores propios y los valores propios, comprender las ecuaciones que hay detrás de ellos es extremadamente valioso. En este apartado, repasaremos lo que se denomina ecuación característica, que calcula paso a paso los vectores propios y los valores propios dada una matriz simple. A continuación, mencionaremos otros métodos de cálculo matemático para matrices más grandes (es decir, grandes conjuntos de datos).

Ecuación característica

Podemos hallar los vectores y valores propios utilizando lo que se conoce como ecuación característica. Utilizando la ecuación característica, los valores propios se encuentran primero antes que los vectores propios. Una vez conocido el valor propio, se utiliza para calcular el vector propio correspondiente resolviendo un sistema de ecuaciones lineales. 

Paso 1: Empieza con la ecuación de transformación de la matriz

Para una matriz 𝐴 y un vector 𝑣la ecuación básica para los vectores y valores propios es

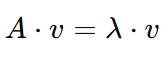
Esto significa que cuando la matriz 𝐴 actúa sobre el vector 𝑣, el resultado es una versión escalada de 𝑣. Toma:

• 𝐴 es una matriz (una cuadrícula cuadrada de números).
• 𝑣 es el vector propio
• λ (lambda) es el valor propio.

Tengamos en cuenta que el objetivo es encontrar tanto λ (el valor propio) y 𝑣 (el vector propio).

Paso 2: Reorganiza la ecuación

Para proceder a nuestro objetivo, necesitamos resolver λ. Por tanto, primero reorganizaremos la ecuación para que sea más fácil trabajar con ella, trasladando el lado derecho al lado izquierdo con signo inverso:

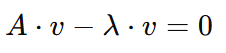
Ahora podemos factorizar 𝑣, pero como 𝐴 es una matriz y 𝑣 es un vector, tendremos que multiplicar 𝑣 por lo que se llama una matriz identidad, denotada como I .Una matriz identidad es una matriz cuadrada (de tamaño nxn) con 1 en su diagonal y 0 en el resto. Debido a la característica de la multiplicación de matrices, una matriz identidad actúa como el número 1 de las matrices. Tomemos, por ejemplo, esta matriz identidad de tamaño 3x3:

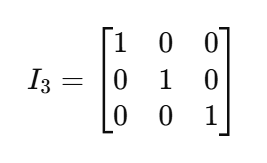
Volviendo a nuestra ecuación, si factorizamos la 𝑣y lo multiplicamos por Iel resultado sería el siguiente

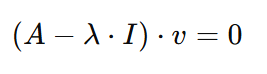
Paso 3: Establece el determinante

Para resolver la ecuación a la que llegamos, o bien el vector propio 𝑣 debe ser cero, o bien el vector propio sería igual a lo que sea 𝐴-λ⋅I. Y ahora es el momento adecuado para decir una cosa más sobre los vectores propios: no pueden ser iguales a cero. Por tanto, 𝐴-λ⋅I debe ser igual a cero. Pero como lambda es la incógnita, podemos conseguir que el lado izquierdo de la ecuación sea igual a su lado derecho si tomamos el determinante de la 𝐴-λ⋅I. Así, llegamos a la siguiente ecuación:

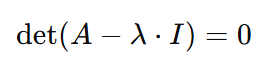
Aquí hemos llegado a la ecuación característica. La resolución de la ecuación característica puede darnos tanto los valores propios λ como el vector propio 𝑣, y se muestra en los pasos restantes.

Paso 4: Resuelve los valores propios

Suponiendo que tenemos la siguiente matriz 𝐴:

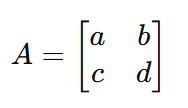
Sustituyendo 𝐴 con la matriz real en la ecuación característica, la ecuación pasa a ser

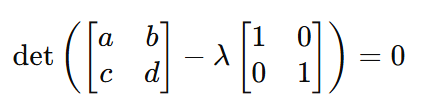
Y por tanto

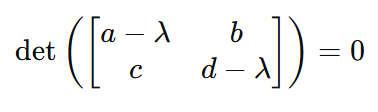
Y, por tanto, una vez más:

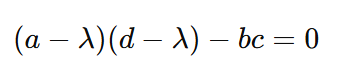
A partir de esta forma mucho más sencilla de la ecuación, podemos calcular los valores de los valores propios λ sustituyendo únicamente los valores de la matriz.

Paso 5: Resuelve los vectores propios 𝑣

Al obtener los valores propios λ, lo que queda es obtener los vectores propios 𝑣. Podemos hacerlo volviendo a esta forma anterior de la ecuación:

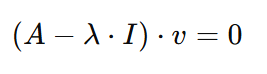
Ahora, si sustituimos 𝐴, λy I con sus valores, podemos calcular fácilmente el valor del vector propio 𝑣.

Métodos de cálculo numérico

Como hemos visto, la complejidad del cálculo de los vectores y valores propios depende en gran medida del tamaño de la matriz. En nuestro ejemplo, hemos utilizado una simple matriz 2x2 𝐴. Pero en la práctica no podemos encontrar los vectores y valores propios de esta forma cuando las matrices son mucho más grandes, como cuando tienen cientos o miles de filas y columnas. En este caso, utilizamos lenguajes de programación como Python y R, que emplean métodos de cálculo numérico frente a métodos simbólicos. Algunas de las técnicas utilizadas son

1. Algoritmo QR: Este es un método habitual para encontrar los valores propios. Implica una secuencia de factorizaciones matriciales(factorizaciones QR) para converger iterativamente a los valores propios.
2. Descomposición Cholesky o LU: Para determinados tipos de matrices (por ejemplo, matrices simétricas o definidas positivamente), se pueden utilizar métodos especializados como la descomposición Cholesky o LU para un cálculo más eficaz.
3. Equilibrar y escalar: Para mejorar la estabilidad numérica, R y Python suelen escalar y equilibrar las matrices antes de realizar los cálculos.

Consideraciones en Ciencia de Datos y Aprendizaje Automático

Los vectores y valores propios son esenciales en muchas aplicaciones, entre ellas las siguientes:

• Tratamiento de imágenes: Se utilizan en el reconocimiento facial y la clasificación de imágenes.
• Procesamiento del Lenguaje Natural (PLN): Los vectores y valores propios se utilizan en el modelado de temas y en la incrustación de palabras.
• Sistemas de recomendación: Como en el filtrado colaborativo y basado en el contenido, donde la reducción de la dimensionalidad puede mejorar la precisión de los sistemas de recomendación.
• Agrupación espectral: Los eigenvectores y los eigenvalores son también un componente fundador de la agrupación espectral, que es un método que agrupa puntos de datos observando sus conexiones en un grafo, utilizando información de la estructura de los datos en lugar de sólo la distancia, que tiene varias aplicaciones prácticas, como en el tratamiento de imágenes.
• Análisis de Componentes Principales: El ACP es una técnica de reducción de la dimensionalidad habitual en el aprendizaje automático. Con el ACP, con hallar los vectores propios de la matriz de covarianza estandarizada y ordenarlos por valor propio. 

Hemos dicho que los valores propios pueden ser cualquier número real o complejo. Eso significa que el valor propio puede ser cero, y también que podemos tener varios valores propios en la matriz analizada que sean iguales. Estos dos casos se consideran dos errores que pueden surgir en cualquier análisis eigen. Echemos un vistazo a cada uno de ellos.

Problema de valor propio cero

Un valor propio cero es un problema porque significa que la transformación de su correspondiente vector propio dio como resultado un vector cero, que puede imaginarse como un único punto en el espacio sin magnitud y, por tanto, no explica ninguna varianza en el conjunto de datos. El problema puede tratarse con técnicas de regularización, como la regresión de cresta (regularización de Tikhonov), o eliminando características colineales (también conocida como reducción de la dimensionalidad), lo que ocurre de forma natural en un algoritmo PCA. Por tanto, el valor propio cero no es un problema para el ACP y, de hecho, el ACP puede ser una solución para él. Sin embargo, para otros algoritmos de aprendizaje automático que implican la resolución de sistemas lineales, como las regresiones lineal, de cresta y de lazo, el problema del valor propio cero debe tratarse de antemano.

Valores propios degenerados

Cuando varios valores propios tienen el mismo valor, se denominan degenerados, y constituyen un problema en la ciencia de datos, sobre todo desde un punto de vista práctico en el ACP y la agrupación espectral. En el ACP, si varios vectores propios tienen valores propios idénticos, significa que estos vectores propios capturan la misma cantidad de varianza en el conjunto de datos y, por tanto, la elección de k componentes principales se vuelve problemática. En la agrupación espectral, en la que los valores propios de la matriz de similitud se utilizan para agrupar los puntos de datos, los valores propios degenerados pueden indicar que los puntos de datos son igualmente similares en múltiples dimensiones, lo que dificulta determinar qué dimensiones o vectores propios deben utilizarse para separar los conglomerados.

Vectores propios, valores propios y composición propia

Cualquier debate sobre los vectores propios y los valores propios no estaría completo sin hablar también de la eigenecomposición. La eigenecomposición es el proceso de descomponer una matriz cuadrada A en sus vectores y valores propios. Para una matriz descomponible, se puede expresar como:

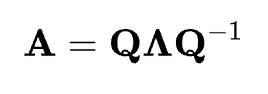
La eigendecomposición nos dice que la matriz A puede expresarse como el producto de su matriz de vectores propios Q, una matriz diagonal Λ de sus valores propios y la inversa de la matriz de vectores propios ^Q-1. Estas matrices, al multiplicarse entre sí en la multiplicación de matrices, reconstruirán la matriz original A. La eigendecomposición es importante porque proporciona una forma de entender y simplificar las transformaciones lineales complejas, proporcionando una visión del comportamiento del sistema, y también simplifica muchos cálculos. 

Conclusión

En este artículo, hemos visto qué son los vectores propios y los valores propios y cómo son extremadamente relevantes para la ciencia de datos y el aprendizaje automático. También repasamos cómo se calculan matemáticamente, así como los errores que pueden surgir al intentar hallar los vectores propios y los valores propios.

Además del curso de Álgebra Lineal en R y el tutorial SciPy sobre vectores y matrices, si te tomas en serio los vectores y valores propios y sus aplicaciones en el aprendizaje automático, prueba nuestro itinerario profesional de Científico de Aprendizaje Automático con Python y conviértete en un experto en aprendizaje supervisado y no supervisado, incluyendo, por supuesto, la reducción de dimensionalidad.