Probabilidad condicional: Una mirada cercana

Imagina que estás desarrollando un sistema de detección de spam para el correo electrónico. Al principio, puedes marcar un correo electrónico como sospechoso si contiene determinadas palabras clave. Pero, ¿y si descubres que este correo electrónico procedía de un remitente de confianza? ¿Y si se envió a una hora inusual? Cada dato nuevo cambia la probabilidad de que el correo electrónico sea spam. Esta actualización dinámica de las probabilidades basada en nuevas pruebas es el núcleo de la probabilidad condicional, un concepto que impulsa muchas aplicaciones modernas de la ciencia de datos, desde el filtrado del correo electrónico a la detección del fraude. 

Para los que se inician en los conceptos de probabilidad, la Hoja de trucos de Introducción a las reglas de probabilidad proporciona una referencia útil para los principios y fórmulas básicos. El curso Introducción a la Estadística construye una base sólida explorando las distribuciones de probabilidad y sus propiedades, que constituyen la base para comprender cómo funciona en la práctica la probabilidad condicional. Estos recursos ofrecen un camino estructurado para desarrollar fundamentos sólidos en los conceptos que exploraremos en este artículo.

¿Qué es la probabilidad condicional?

La probabilidad condicional mide la probabilidad de que ocurra un suceso cuando sabemos que ya ha ocurrido otro. Cuando recibimos nueva información sobre un acontecimiento, ajustamos nuestros cálculos de probabilidad en consecuencia.

Para entender este concepto, exploremos un ejemplo con cartas. Cuando sacas una carta de una baraja normal, hay 52 resultados posibles. Si quieres sacar un rey, tu probabilidad inicial es de 4/52 (aproximadamente un 7,7%), ya que hay cuatro reyes en la baraja. Pero, ¿qué ocurre si alguien te dice que la carta que has sacado es una carta descubierta? Esta nueva información lo cambia todo: tu probabilidad de tener un rey es ahora mucho mayor, de 4/12 (aproximadamente un 33,3%), ya que sólo hay doce cartas de cara en total.

Esta relación entre probabilidades tiene una definición matemática precisa:

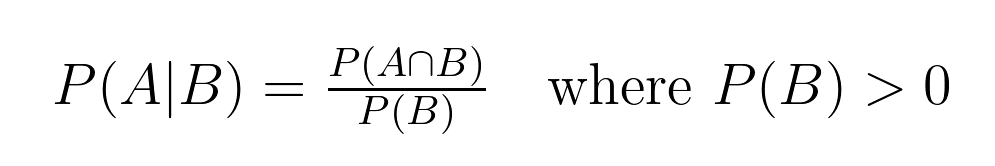
Esta fórmula nos ayuda a calcular la probabilidad condicional, donde:

• P(A|B) representa la probabilidad de que ocurra el suceso A, dado que ha ocurrido el suceso B. Esto se lee como "la probabilidad de A dado B".
• P(A∩B) representa la probabilidad conjunta, o probabilidad de que ocurran juntos los sucesos A y B. Esto se lee como "la probabilidad de que A se cruce con B".
• P(B) representa la probabilidad de que ocurra el suceso B.

En nuestro ejemplo de tarjeta:

• El Evento A es "sacar un Rey"
• El suceso B es "sacar una carta descubierta"
• P(A|B) = 4/12 (probabilidad de obtener un rey, dado que tenemos una carta descubierta)
• P(A∩B) = 4/52 (probabilidad de sacar un rey, que siempre es una carta descubierta)
• P(B) = 12/52 (probabilidad de sacar cualquier carta descubierta)

Para comprender mejor cómo funciona la probabilidad condicional en la práctica, podemos utilizar un diagrama de árbol. Los diagramas de árbol son especialmente útiles porque muestran cómo cada nueva información cambia nuestras probabilidades:

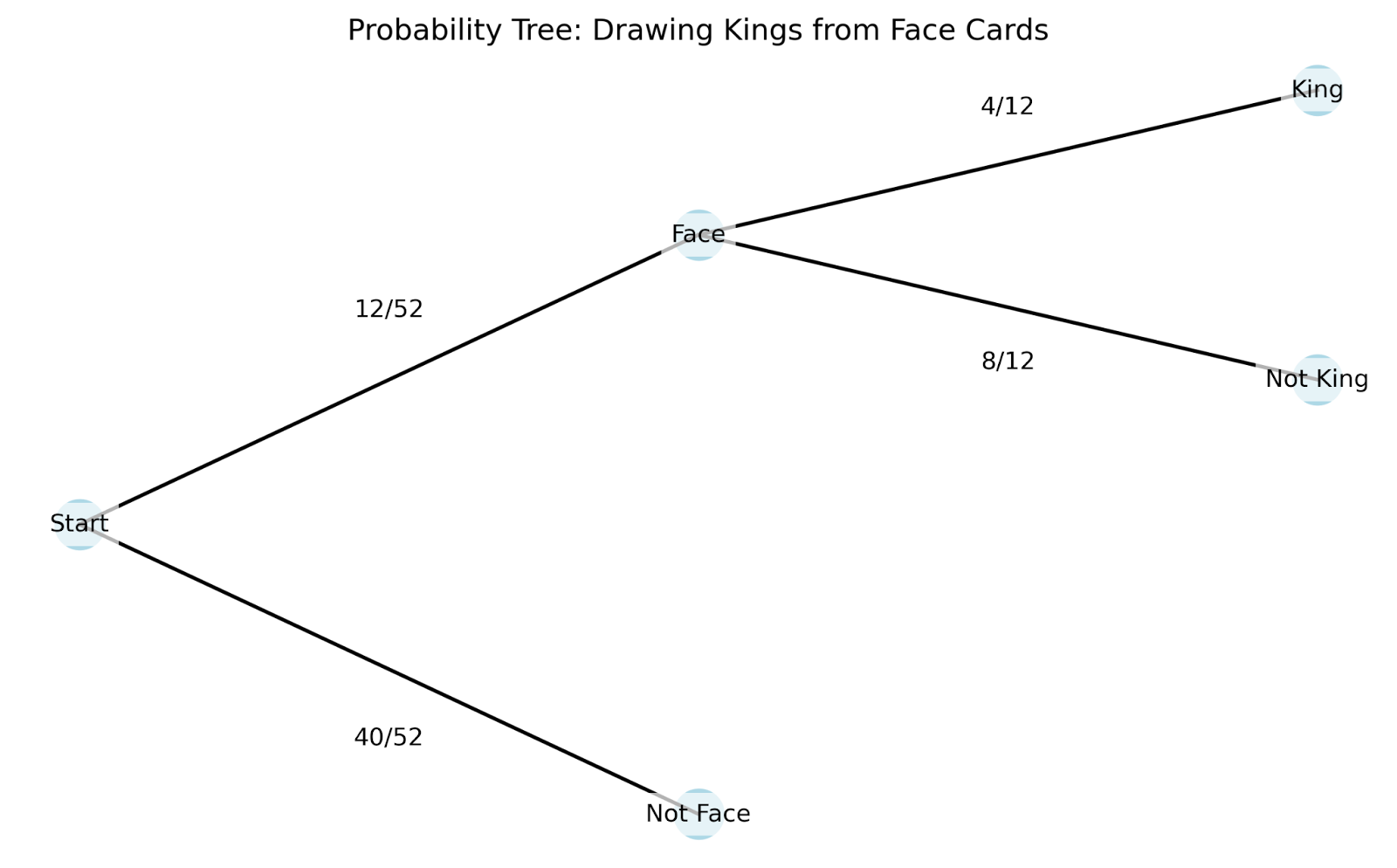
Veamos cómo funciona este diagrama de árbol:

1. Empezamos en la raíz (punto más a la izquierda) con las 52 cartas.
2. Las primeras ramas muestran nuestra primera información: ¿es una carta con cara o no?
3. Si seguimos la rama de las cartas de la cara, se divide de nuevo en función de nuestro segundo dato: ¿es un rey?

El diagrama de árbol nos ayuda a comprender varios conceptos clave de la probabilidad condicional:

• Espacio de muestra: Estos son todos los resultados posibles en nuestro escenario. El espacio muestral inicial es de 52 cartas, pero se "reduce" a 12 cartas una vez que sabemos que tenemos una carta con cara.
• Eventos: Son resultados concretos que nos interesan, como "sacar una carta cara" o "sacar un rey". Las ramas de nuestro árbol representan distintos acontecimientos.
• Probabilidad conjunta: Es la probabilidad de que se produzcan varios sucesos a la vez. En nuestro árbol, podemos encontrarlo multiplicando las probabilidades a lo largo de un camino. Por ejemplo, la probabilidad de sacar un rey Y que sea una carta descubierta es (12/52) × (4/12) = 4/52.
• Probabilidad marginal (incondicional): Es la probabilidad de que ocurra un suceso sin tener en cuenta ninguna otra información. En nuestro ejemplo, es como la probabilidad inicial de 4/52 de sacar un rey antes de saber nada más sobre la carta.

La belleza de la probabilidad condicional es que nos permite actualizar nuestras probabilidades a medida que obtenemos nueva información. Del mismo modo que ajustamos nuestra probabilidad de tener un rey del 7,7% al 33,3% cuando supimos que teníamos una carta cara, la probabilidad condicional nos da una forma formal de recalcular probabilidades basándonos en nuevas pruebas.

La fórmula de la probabilidad condicional

La estructura matemática de la probabilidad condicional nos proporciona herramientas para analizar escenarios complejos en los que intervienen múltiples sucesos. Exploremos las propiedades clave.

Propiedades clave de la probabilidad condicional

Estas propiedades matemáticas nos ayudan a resolver problemas complejos con mayor eficacia:

1. Propiedad independiente

Cuando dos sucesos A y B son independientes, sabemos que la ocurrencia de uno no afecta a la probabilidad del otro. Matemáticamente, esto es: P(A|B) = P(A), que se lee como: "la probabilidad de A dada B es igual a la probabilidad de A".

Por ejemplo, si tiramos un dado y lanzamos una moneda, sacar cara en la moneda no cambia la probabilidad de sacar un seis. La fórmula nos lo indica: P(Seis|Cabezas) = P(Seis) = 1/6

2. Regla del complemento

Para cualquier suceso A dada la condición B, las probabilidades de A y su complemento A' (leído como "A primo") deben sumar 1. Matemáticamente, esto es: P(A|B) + P(A'|B) = 1, que se lee como: "La probabilidad de A dada B más la probabilidad del complemento de A dada B es igual a 1".

En nuestro ejemplo anterior de la tarjeta: P(Rey|Carta Cara) + P(No Rey|Carta Cara) = 4/12 + 8/12 = 1

La regla de la multiplicación y la regla de la cadena

La regla de multiplicación vincula las probabilidades conjuntas con las probabilidades condicionales: P(A ∩ B) = P(A|B) × P(B). Decimos: "La probabilidad de A intersección B es igual a la probabilidad de A dada B multiplicada por la probabilidad de B".

Esto se extiende a múltiples eventos a través de la regla de la cadena. Para tres acontecimientos A, B y C: P(A ∩ B ∩ C) = P(A|B ∩ C) × P(B|C) × P(C). Es decir, "La probabilidad de A intersección B intersección C es igual a la probabilidad de A dada B intersección C multiplicada por la probabilidad de B dada C multiplicada por la probabilidad de C".

Veámoslo en acción con una secuencia de extracción de cartas:

1. Sacar un rey (K)
2. De las cartas restantes, sacar una reina (Q)
3. De las cartas restantes, saca un as (A)

P(K ∩ Q ∩ A) = P(A|K ∩ Q) × P(Q|K) × P(K) = (4/50) × (4/51) × (4/52)

La regla de la cadena resulta especialmente valiosa en el aprendizaje automático, sobre todo en las redes bayesianas, donde necesitamos modelar dependencias complejas entre múltiples variables. Al analizar datos, a menudo nos encontramos con situaciones en las que los acontecimientos siguen una secuencia natural, y la regla de la cadena nos ayuda a descomponer estos escenarios complejos en cálculos más sencillos y manejables.

Ejemplos para ilustrar la probabilidad condicional

Repasemos dos de los ejemplos más comunes y piensa también en cómo podría aparecer la probabilidad condicional en tu trabajo.

Ejemplos clásicos

Estos dos ejemplos son muy comunes y merece la pena estudiarlos, sobre todo si vas a hacer una entrevista:

Tiradas de dados: Comprender los espacios muestrales reducidos

Cuando lanzamos un dado, nuestro espacio muestral comienza con seis posibilidades: {1, 2, 3, 4, 5, 6}. Aprender información parcial sobre la tirada cambia nuestros cálculos de probabilidad de una manera específica. Veamos cómo:

Probabilidad inicial de sacar un 6: P(6) = 1/6

Si nos enteramos de que la tirada era par, nuestro espacio muestral se reduce a {2, 4, 6}: P(6 | par) = 1/3

Canicas: Dependencias secuenciales

Una bolsa contiene 5 canicas azules y 3 canicas rojas. Cuando sacamos canicas sin reemplazo, cada extracción afecta a las probabilidades de las siguientes.

Primer sorteo - probabilidad de azul: P(blue₁) = 5/8

Segundo sorteo, dado que el primero fue azul: P(blue₂ | blue₁) = 4/7

Este ejemplo complementa nuestro anterior ejemplo de la tarjeta al poner de relieve las dependencias secuenciales.

Ejemplos reales

Pruebas médicas: Evaluar la precisión de las pruebas

Las pruebas médicas ofrecen una aplicación perfecta de la probabilidad condicional para evaluar la precisión de las pruebas. Para cualquier prueba diagnóstica, necesitamos comprender cuatro probabilidades condicionales clave:

1. P(T+ | D+): Probabilidad de una prueba positiva si el paciente tiene la enfermedad (sensibilidad) 
2. P(T- | D-): Probabilidad de una prueba negativa dado que el paciente no tiene la enfermedad (especificidad) 
3. P(T+ | D-): Probabilidad de un resultado positivo si el paciente no tiene la enfermedad (tasa de falsos positivos) 
4. P(T- | D+): Probabilidad de una prueba negativa dado que el paciente tiene la enfermedad (tasa de falsos negativos)

Al evaluar el rendimiento de esta prueba, los profesionales médicos utilizan estas probabilidades condicionales para:

1. Comparar la precisión de las pruebas en diferentes poblaciones de pacientes
2. Determina cuándo pueden ser necesarias varias pruebas
3. Establece umbrales adecuados para los resultados positivos/negativos

Por ejemplo, si analizamos a 1000 pacientes y obtenemos 100 resultados positivos, podemos utilizar estas probabilidades condicionales para estimar cuántos son verdaderos positivos frente a falsos positivos. Este análisis ayuda a los profesionales médicos a sopesar los riesgos de omitir un diagnóstico frente a los costes y la ansiedad de las falsas alarmas.

Evaluación del riesgo financiero

Las empresas de inversión utilizan la probabilidad condicional para evaluar los riesgos del mercado. Piensa en un gestor de cartera que sigue la volatilidad del mercado:

La volatilidad diaria del mercado puede ser Baja (L), Media (M) o Alta (H).

Los datos históricos lo demuestran: 

• P(H mañana | H hoy) = 0,70 
• P(M mañana | H hoy) = 0,25 
• P(L mañana | H hoy) = 0,05

Esta información ayuda a los gestores:

• Ajustar las asignaciones de la cartera en función de las condiciones actuales del mercado
• Establecer umbrales de riesgo para los sistemas automatizados de negociación
• Desarrollar planes de contingencia para periodos de alta volatilidad sostenida

Probabilidad condicional y teorema de Bayes

Nuestra exploración de las pruebas médicas puso de relieve una distinción importante: La probabilidad de tener una enfermedad dada una prueba positiva difiere de la probabilidad de dar positivo dada la enfermedad. El Teorema de Bayes proporciona un marco formal para navegar por esta relación, permitiéndonos actualizar nuestras estimaciones de probabilidad a medida que surgen nuevas pruebas.

Comprender el Teorema de Bayes

El Teorema de Bayes expresa la relación entre dos probabilidades condicionales: P(A|B) = [P(B|A) × P(A)] / P(B). Leemos esta ecuación de esta manera: "La probabilidad de A dada B es igual a la probabilidad de B dada A multiplicada por la probabilidad de A, dividida por la probabilidad de B".

Cada componente desempeña una función:

• P(A): La probabilidad previa - nuestra creencia inicial sobre A antes de ver la prueba B
• P(B|A): La probabilidad - cómo de probable es la prueba B si A es cierta
• P(B): La probabilidad total de observar la prueba B
• P(A|B): La probabilidad posterior - nuestra creencia actualizada sobre A después de ver la prueba B

Veamos cómo funciona en la práctica con nuestro escenario de pruebas médicas, ahora ampliado para mostrar el análisis bayesiano completo.

Un ejemplo de pruebas médicas

Considera una enfermedad que afecta al 2% de la población. Se ha realizado una nueva prueba diagnóstica:

• Sensibilidad del 95%: P(prueba positiva | tiene condición) = 0,95
• 90% de especificidad: P(prueba negativa | ninguna condición) = 0,90

Cuando un paciente da positivo, ¿cómo debemos actualizar nuestra creencia sobre su estado?

Vamos a resolverlo paso a paso:

1. Probabilidad previa (antes de la prueba): P(condición) = 0,02 (tasa de población del 2%)
2. Probabilidad de una prueba positiva dada la afección: P(positivo|condición) = 0,95 (sensibilidad de la prueba)
3. Probabilidad total de una prueba positiva: P(positivo) = P(positivo|condición) × P(condición) + P(positivo|sin condición) × P(sin condición) = 0,95 × 0,02 + 0,10 × 0,98 = 0,019 + 0,098 = 0,117
4. Probabilidad posterior (utilizando el Teorema de Bayes): P(condición|positiva) = [0,95 × 0,02] / 0,117 ≈ 0,162 ó 16,2%.

Este análisis revela que, incluso con una prueba positiva, la probabilidad de padecer la enfermedad es sólo de un 16,2%, mucho mayor que el 2% inicial, pero quizá menor de lo que podría sugerir la intuición.

El poder de la actualización bayesiana

El Teorema de Bayes brilla cuando recibimos múltiples pruebas. La probabilidad posterior de cada cálculo se convierte en la probabilidad a priori de la siguiente actualización. Por ejemplo, si nuestro paciente obtiene un segundo resultado positivo:

1. Nuevo prior: P(condición) = 0,162 (de nuestro primer cálculo)
2. Probabilidad: P(positivo|condición) = 0,95
3. Calcula el nuevo...

Esta actualización secuencial proporciona un marco matemático para incorporar nuevas pruebas a nuestras estimaciones de probabilidad. La belleza de la inferencia bayesiana reside en su capacidad para cuantificar cómo deben cambiar nuestras creencias a medida que reunimos nueva información, proporcionando un método formal para actualizar las probabilidades a la luz de las pruebas.

Aplicaciones en Ciencia de Datos

Veamos cómo aparece la probabilidad condicional en la ciencia de datos. 

Modelización predictiva

El clasificador Naive Bayes, una de las herramientas más sencillas pero potentes del aprendizaje automático, aplica el Teorema de Bayes para predecir categorías basándose en las probabilidades de las características. Al clasificar un correo electrónico como spam o no spam, por ejemplo, el algoritmo calcula la probabilidad condicional de que un correo electrónico sea spam dadas las palabras que contiene. Aunque hace la suposición "ingenua" de que los rasgos son independientes, esta simplificación suele funcionar sorprendentemente bien en la práctica.

Los árboles de decisión adoptan un enfoque diferente de la probabilidad condicional, dividiendo los datos en función de los valores de las características para crear subconjuntos condicionales. En cada nodo, el árbol plantea preguntas como "¿Cuál es la probabilidad de nuestra variable objetivo dado este valor de característica específico?" Estas divisiones continúan hasta que llegamos a subconjuntos puros o casi puros, creando esencialmente un mapa de probabilidades condicionales que guían nuestras predicciones.

Gestión de riesgos

Los sistemas de puntuación crediticia utilizan probabilidades condicionales para evaluar la probabilidad de impago de un préstamo dadas varias características del cliente. Por ejemplo, un banco podría calcular la probabilidad de impago teniendo en cuenta el nivel de ingresos, el historial crediticio y la situación laboral. Estos cálculos se vuelven más sofisticados cuando se consideran múltiples riesgos dependientes, como por ejemplo cómo podría cambiar la probabilidad de impago de una hipoteca en caso de recesión y de subida de los tipos de interés. Los modelos de riesgo de inversión utilizan probabilidades condicionales para estimar el Valor en Riesgo (VaR), calculando la probabilidad de niveles de pérdida específicos dadas las condiciones actuales del mercado. Los gestores de cartera utilizan estas probabilidades condicionales para ajustar las asignaciones de activos, comprendiendo cómo podría cambiar el riesgo de una inversión en función del rendimiento de otras de la cartera.

Aprendizaje automático

Las redes bayesianas representan la aplicación más directa de la probabilidad condicional en el aprendizaje automático, modelando las relaciones entre variables como un grafo dirigido en el que el estado de cada nodo depende de sus padres. Estas redes destacan en tareas como el diagnóstico médico, donde la probabilidad de diversas afecciones depende de múltiples síntomas y resultados de pruebas interconectados.

Los modelos gráficos probabilísticos utilizan dependencias condicionales para representar relaciones complejas en los datos, lo que los hace valiosos para tareas como el reconocimiento de imágenes y el procesamiento del lenguaje natural. Incluso los modelos de aprendizaje profundo, aunque no sean explícitamente probabilísticos, emiten probabilidades condicionales en sus capas finales cuando realizan clasificaciones. La función softmax, utilizada habitualmente en las redes neuronales, transforma las puntuaciones brutas en probabilidades condicionales, indicándonos la probabilidad de cada clase posible dados los datos de entrada.

Errores comunes e interpretaciones erróneas

Cuando se trabaja con la probabilidad condicional, hay tres errores principales que suelen llevar a conclusiones incorrectas.

• La falacia inversa, también conocida como confusión de la inversa, se produce cuando confundimos P(A|B) con P(B|A). Lo vimos en nuestro ejemplo de las pruebas médicas: la probabilidad de tener una enfermedad si la prueba da positivo difiere de la probabilidad de dar positivo si tienes la enfermedad.
• El descuido de la tasa base ocurre cuando nos centramos en las probabilidades condicionales ignorando la probabilidad subyacente de un suceso. Por ejemplo, si una enfermedad rara afecta sólo a 1 de cada 10.000 personas, incluso una prueba muy precisa podría dar mayoritariamente falsos positivos simplemente porque la enfermedad es muy poco frecuente.
• El tercer escollo consiste en ponderar incorrectamente las pruebas al actualizar las probabilidades. La gente tiende a sobrevalorar las pruebas recientes o dramáticas, mientras que infravalora la información de fondo estable. En el comercio financiero, por ejemplo, los inversores pueden reaccionar exageradamente a las noticias recientes del mercado ignorando las probabilidades de mercado a largo plazo.

Temas avanzados y otras consideraciones

Por último, veamos algunas ideas más complicadas que se basan en lo que hemos estado practicando.

Condicionar a sucesos de probabilidad cero

Cuando pasamos de distribuciones de probabilidad discretas a continuas, nos encontramos con un reto interesante: determinados puntos de una distribución continua tienen probabilidad cero. Considera la medición de la altura exacta de alguien: mientras que podríamos decir que la probabilidad de que alguien mida entre 170 y 171 centímetros es significativa, la probabilidad de que alguien mida exactamente 170,5432... centímetros es técnicamente cero. Sin embargo, a menudo queremos condicionarnos a medidas tan precisas. La probabilidad condicional regular proporciona un marco matemático para tratar estas situaciones, ampliando nuestros conceptos básicos a los casos continuos mediante el uso de funciones de densidad y teoría de medidas. Esta extensión nos permite dar sentido a afirmaciones como "la distribución de probabilidad del peso de una persona, dado que mide exactamente 170,5 centímetros".

Probabilidad condicional parcial y extensiones

La condicionalización de Jeffrey amplía la probabilidad condicional tradicional a situaciones en las que nuestra nueva prueba no es cierta, sino que viene acompañada de su propia probabilidad. A diferencia del condicionamiento estándar, en el que asumimos una certeza absoluta sobre nuestra nueva información, la regla de Jeffrey nos permite actualizar nuestras creencias basándonos en pruebas inciertas. Esto se ajusta mejor a los escenarios del mundo real, donde la nueva información suele venir acompañada de cierto grado de incertidumbre. Por ejemplo, en lugar de saber con certeza que una prueba médica es positiva, podríamos saber que tiene un 80% de probabilidades de ser positiva. La regla de Jeffrey proporciona un método formal para actualizar las probabilidades en estas situaciones más matizadas.

Conclusión

La probabilidad condicional proporciona un marco matemático para actualizar nuestras creencias a medida que surge nueva información. A lo largo de este artículo, hemos visto cómo este concepto se aplica en diversos campos, desde el diagnóstico médico a la evaluación del riesgo financiero. Los principios que hemos explorado nos ayudan a comprender cómo cambia la probabilidad con nuevas pruebas, lo que permite tomar decisiones más informadas en las aplicaciones de la ciencia de datos. Esta comprensión resulta especialmente valiosa cuando se trabaja con algoritmos de clasificación, modelos de riesgo y sistemas de aprendizaje automático en los que las actualizaciones de probabilidad se producen continuamente.

A medida que continúes desarrollando tu experiencia en probabilidad e inferencia estadística, varios cursos pueden mejorar tu comprensión de estos conceptos a través de una lente bayesiana. Nuestro curso Fundamentos del Análisis Bayesiano de Datos en R presenta los principios clave y sus aplicaciones prácticas, mientras que nuestro curso Modelización Bayesiana con RJAGS muestra cómo aplicar estos conceptos utilizando potentes herramientas estadísticas. Para los usuarios de Python, nuestro curso de Análisis Bayesiano de Datos en Python ofrece experiencia práctica en la aplicación de estos métodos a problemas del mundo real. Cada curso proporciona una vía para ampliar tus conocimientos sobre la probabilidad y sus aplicaciones en la ciencia de datos moderna.