Lei dos grandes números: Uma chave para entender a incerteza

Um resultado por si só não diz muito a você. Suponha que você jogue uma moeda uma vez e obtenha cara. Isso não prova nada - ele pode ter caído dessa forma por acaso. Mas se você jogar a moeda 100 vezes, verá cara e coroa em números praticamente iguais. É nesse momento que a média começa a fazer sentido.

E é disso que trata a lei dos grandes números. Quanto mais dados você coletar, mais precisa será a sua média. Isso ajuda você a ver o panorama geral.

Neste guia, explicaremos o que significa a lei dos grandes números, como ela funciona na vida real e por que é tão útil quando você tenta entender padrões ou tomar decisões melhores ao longo do tempo.

O que é a Lei dos Grandes Números?

A lei dos grandes números é um princípio de probabilidade e estatística que explica como as médias se comportam à medida que mais dados são coletados. À medida que o tamanho da amostra aumenta, a média dessa amostra (chamada de média amostral) se aproxima da média real de todo o grupo (chamada de média populacional).

No mundo real, geralmente não temos acesso aos dados de uma população inteira. Em vez disso, pegamos uma amostra como uma pesquisa com 1.000 eleitores, em vez de todos os 300 milhões de pessoas. A lei dos grandes números nos dá a certeza de que, com dados suficientes, a média da amostra será próxima da realidade.

À medida que a amostra cresce, a variação aleatória começa a ser cancelada. As exceções têm menos impacto, e a média se torna mais estável e previsível.

Há duas versões principais da lei, e elas diferem quanto ao grau de garantia desse efeito:

Lei fraca (convergência na probabilidade)

A lei fraca dos grandes números diz que a média da amostra provavelmente se aproxima da média da população à medida que o tamanho da amostra aumenta. Quanto mais dados você coletar, menor será a probabilidade de sua média ficar longe da marca.

Por exemplo, você joga uma moeda justa. À medida que você joga mais vezes, a proporção de cara e coroa fica mais próxima de 50/50. Você pode não conseguir um resultado perfeito, mas chega bem perto, e é disso que trata a lei fraca.

Lei forte (convergência quase certa)

A forte lei dos grandes números vai um passo além. Ele diz que a média da amostra se aproximará da média da população e permanecerá lá quase certamente, não apenas provavelmente.

Em termos simples: se você continuar jogando essa moeda justa para sempre, a proporção de cara para coroa não chegará perto de 50/50; ela se estabelecerá ali. Portanto, essa lei nos dá certeza quase total de que as médias de longo prazo refletem a verdade, com raras exceções.

Exemplos reais da lei no trabalho

Vamos dar uma olhada em alguns exemplos reais para que você entenda como essa lei funciona:

Lançamento de moedas ou de dados

Imagine que você rolou um dado normal de seis lados três vezes. Você pode obter resultados como 6, 2 e 5. A média é de 4,3, que é maior do que o valor esperado de 3,5. Mas agora você joga o dado 100 vezes, depois 1.000 vezes. À medida que o número de rolagens aumenta, sua média fica mais próxima de 3,5. A lei dos grandes números suaviza a aleatoriedade ao longo do tempo.

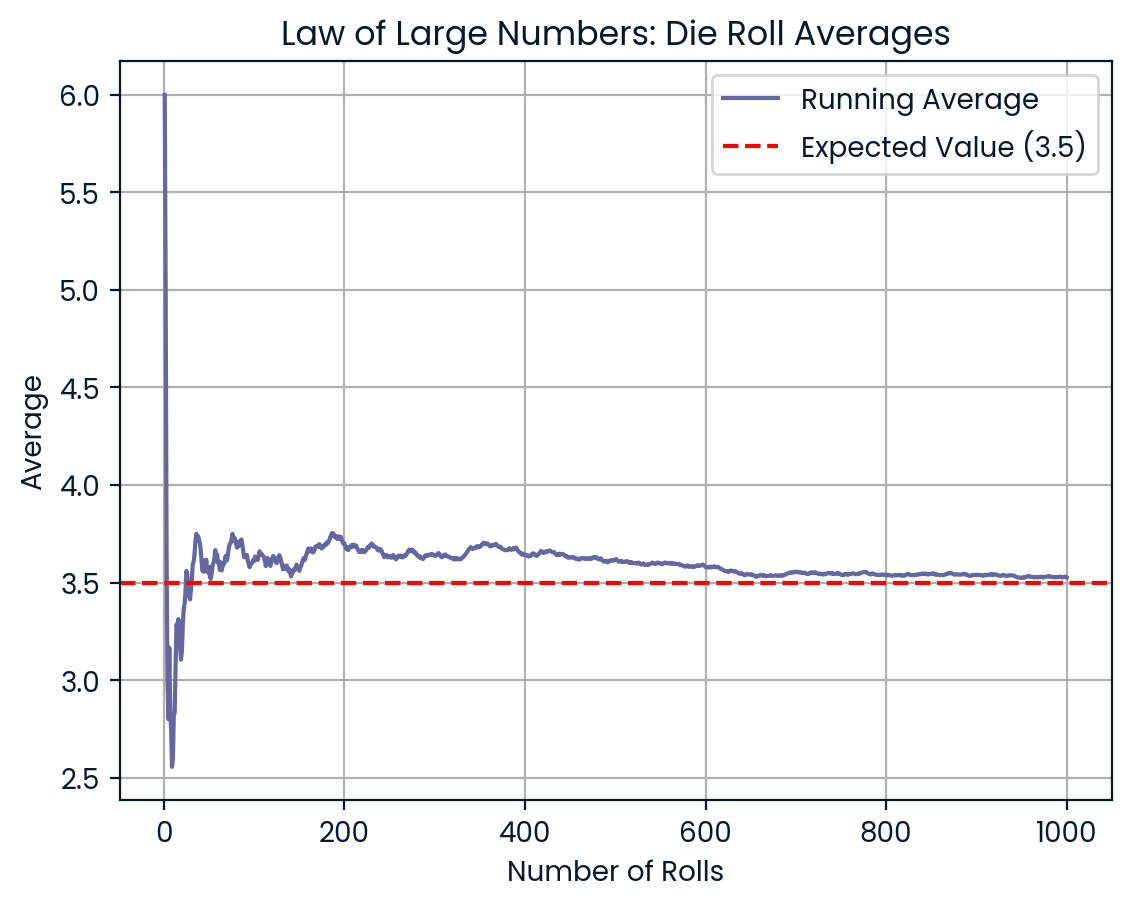
Mais rolagens fazem com que a média se aproxime de 3,5. Imagem do autor.

Estatísticas esportivas

Os atletas podem ter dias bons e dias ruins. Um quarterback pode completar 9 de 10 passes em um jogo, o que representa 90%. Mas isso não significa que eles sempre jogam nesse nível.

Em uma temporada inteira, com centenas de lançamentos, a porcentagem de conclusão começa a se estabilizar. Essa estatística de toda a temporada dá uma noção muito melhor da capacidade real do jogador.

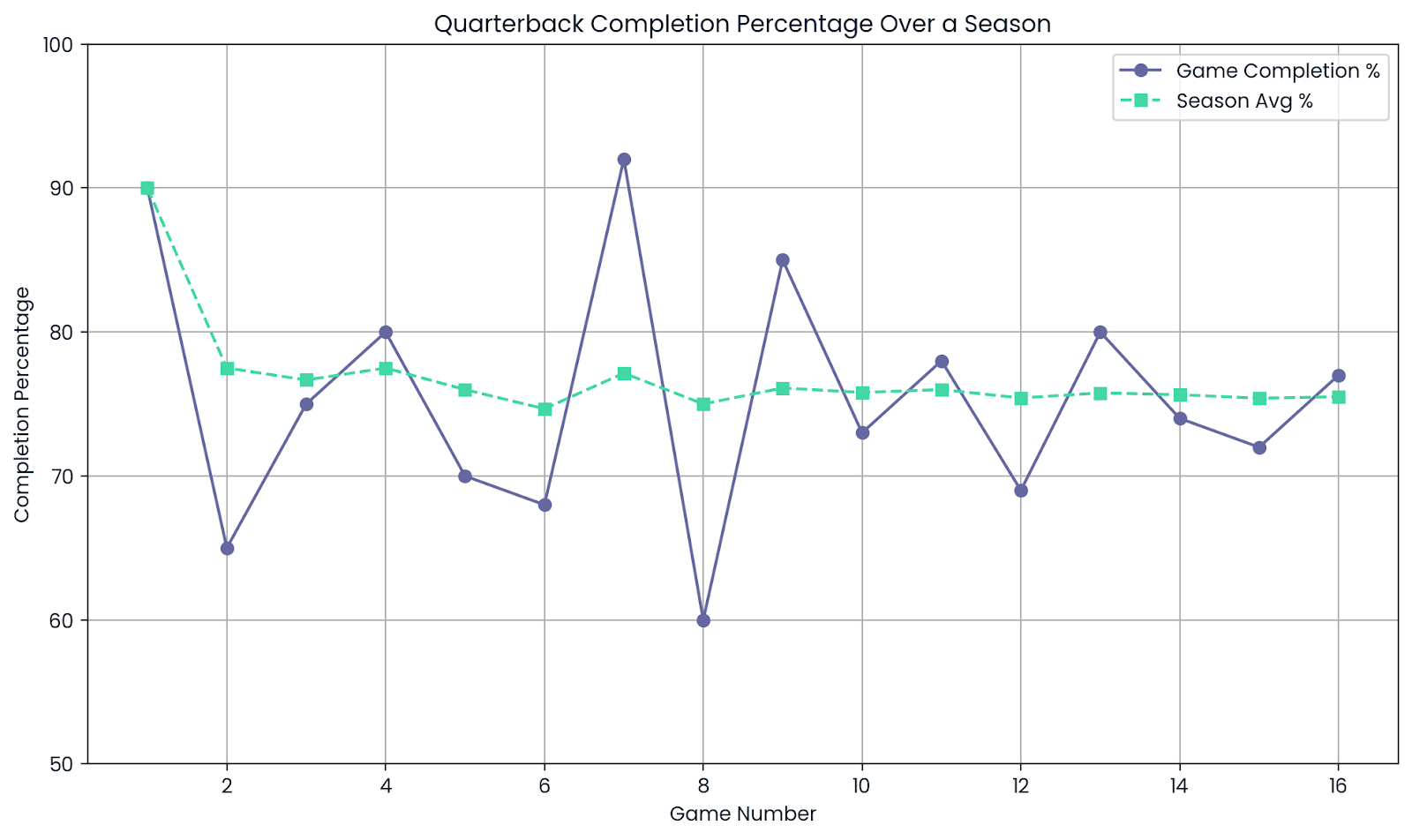
Média. Imagem do autor.

Agrupamento de riscos do setor de seguros 

As seguradoras não sabem exatamente quanto uma pessoa custará a elas. Algumas pessoas não usam nenhum tipo de assistência médica, enquanto outras usam.

Mas quando você observa um grande grupo de pessoas, esses altos e baixos se equilibram. Ao agrupar o risco entre milhares de segurados, as seguradoras podem prever o custo médio com mais precisão.

Isso permite que eles estabeleçam preços justos (prêmios) e permaneçam financeiramente estáveis.

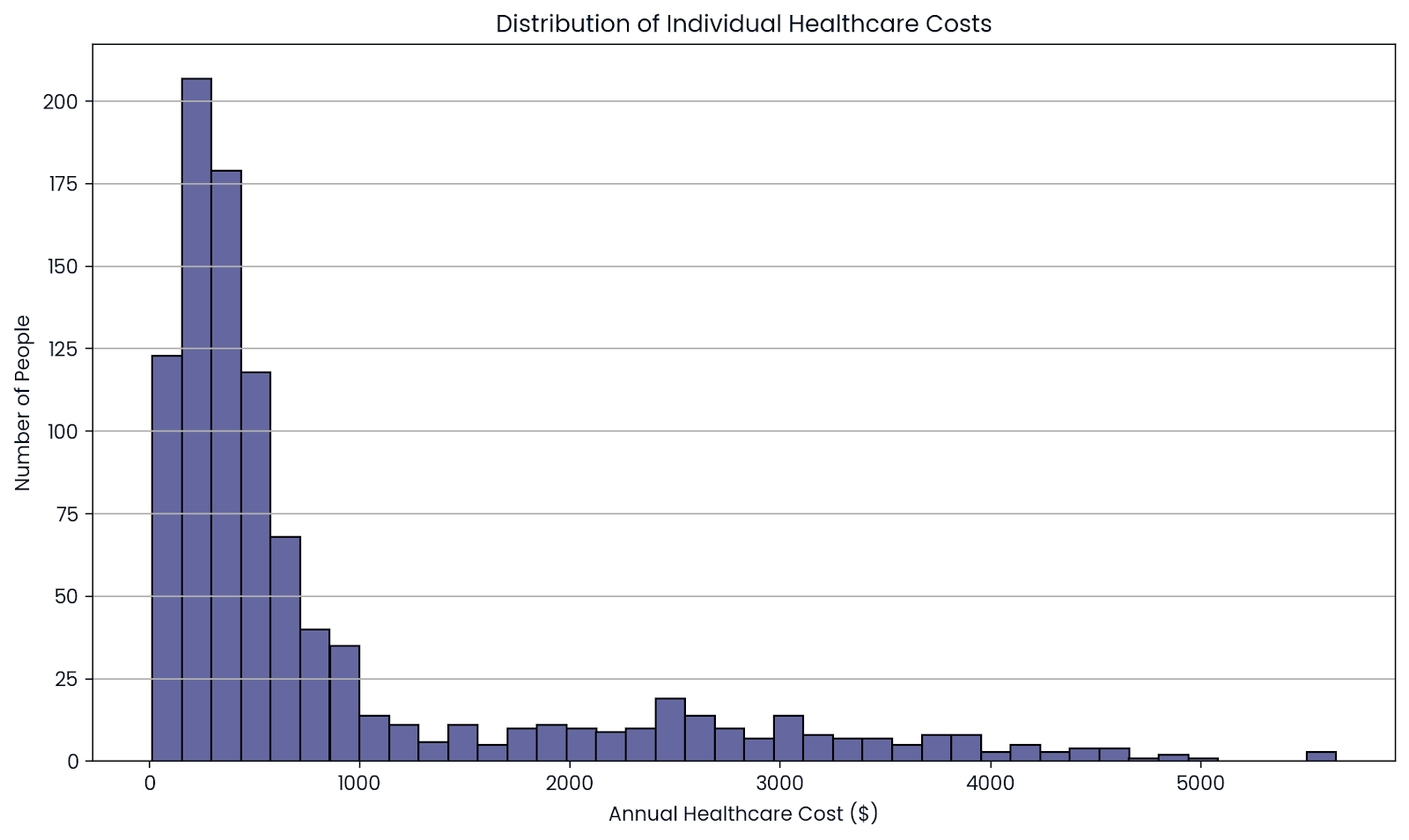
A média de muitas pessoas mostra o custo real. Imagem do autor.

Jogos de cassino e vantagem da casa

Os cassinos têm uma pequena vantagem em todos os jogos. Se você joga blackjack, pode ganhar cinco mãos seguidas ou perder dez. Porém, em milhares de jogos, o resultado médio favorece o cassino.

Por exemplo, se a margem da casa for de 0,5%, então, ao longo do tempo, o cassino espera ganhar 50 centavos de dólar para cada US$ 100 apostados, em média. Isso pode não acontecer em uma sessão curta, mas, ao longo de milhões de jogadas, o resultado é exatamente o esperado.

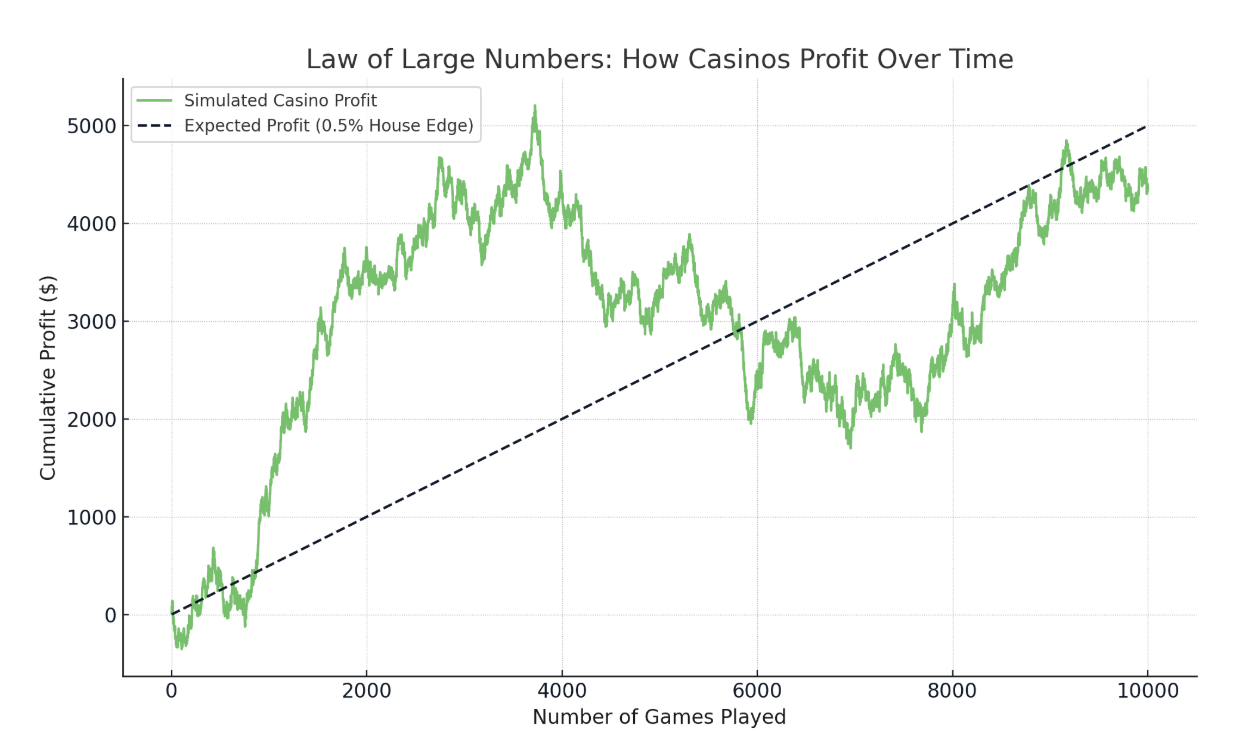
A vantagem do cassino vence com mais apostas. Imagem do autor.

Testes A/B em empresas de tecnologia

Suponha que uma empresa queira testar duas versões de um botão do site: Botão A e Botão B. Após 20 pessoas experimentarem cada um, o Botão A parece melhor. Mas esses dados não são suficientes para que você confie no resultado.

Agora, permita que 20.000 usuários vejam ambos. À medida que o tamanho da amostra aumenta, as taxas médias de cliques se tornam mais confiáveis, e o botão com melhor desempenho fica claro.

É por isso que as empresas dependem de grandes amostras para testes A/B. A lei dos grandes números os ajuda a evitar falsos positivos e a fazer escolhas mais inteligentes.

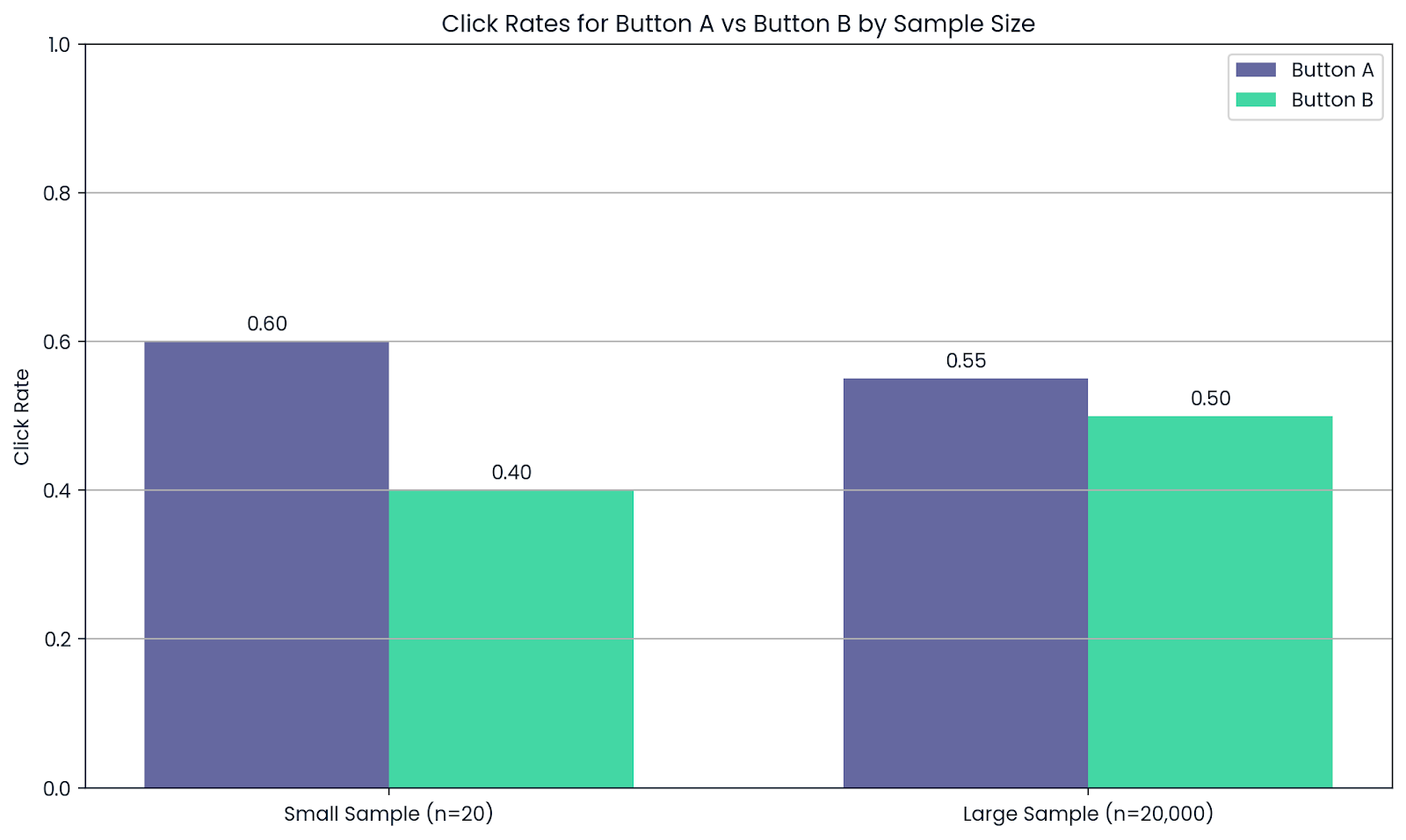
Mais pessoas testadas significam resultados mais confiáveis. Imagem do autor.

Por que a Lei dos Grandes Números é importante

Na ciência de dados, geralmente usamos dados para treinar modelos. Mas se o conjunto de dados for muito pequeno, alguns valores incomuns podem distorcer os resultados.

Por exemplo, você está testando um novo algoritmo de recomendação usando apenas 10 usuários. Se um usuário clica em tudo e outro não clica em nada, seu desempenho médio pode parecer ótimo ou péssimo. Isso não significa que o modelo seja bom ou ruim; significa que a amostra é muito pequena para que você possa confiar nela.

A lei dos grandes números nos diz que, à medida que coletamos mais dados, as flutuações aleatórias se equilibram e o resultado médio se torna mais confiável. É por isso que grandes conjuntos de dados oferecem melhores previsões e percepções.

Você também vê isso em simulações. Veja os métodos de Monte Carlo, por exemplo. Isso envolve a execução do mesmo cenário milhares de vezes usando entradas aleatórias. A lei dos grandes números garante que, quanto mais tentativas forem realizadas, mais o resultado médio se aproximará do resultado esperado verdadeiro.

No machine learning, a lei aparece de duas maneiras importantes:

• Treinamento de modelos: Um modelo treinado em um conjunto de dados pequeno e desequilibrado pode aprender padrões que não refletem o mundo real. Mas com dados diversificados suficientes, o modelo aprende o que realmente funciona.
• Teste de modelo: Testar um modelo em apenas 50 usuários pode gerar resultados muito diferentes do que testá-lo em 5.000. Um conjunto de testes maior oferece uma visão mais clara do desempenho do modelo quando ele for implantado.

Em resumo, mais dados significam menos ruído e melhores decisões. 

Equívocos comuns

A lei dos grandes números é frequentemente mal interpretada quando as pessoas esperam que ela funcione instantaneamente.

Se você acredita que os resultados "se equilibrarão" rapidamente, isso é um erro. Por exemplo, se você jogar uma moeda e tirar cara cinco vezes seguidas, poderá pensar que a coroa agora é "devida" para equilibrar as coisas. Mas não é assim que a probabilidade funciona.

Esse pensamento é conhecido como falácia do apostador: a falsa ideia de que os resultados anteriores influenciam os futuros em um processo verdadeiramente aleatório. Na realidade, cada lançamento de moeda continua sendo uma chance de 50/50, independentemente do que tenha acontecido antes.

A lei dos grandes números não promete que a aleatoriedade será suavizada no curto prazo. Em vez disso, ele nos diz que, ao longo de muitas e muitas tentativas, o resultado médio se aproxima do valor esperado. No caso de uma moeda justa, isso significa aproximadamente metade cara e metade coroa, eventualmente, não imediatamente.

Ainda assim, você pode ter pequenas sequências ou padrões incomuns ao longo do caminho. É assim que a aleatoriedade aparece em pequenas amostras. A lei só se torna significativa quando você diminui o zoom e olha para o quadro geral.

Como ele se relaciona com outros conceitos

Embora a lei dos grandes números nos diga que a média da amostra se aproxima da média verdadeira à medida que o tamanho da amostra aumenta, o teorema do limite central (CLT) vai além. Ele explica como é a distribuição dessas médias.

De acordo com a CLT, se você pegar muitas amostras grandes e calcular suas médias, essas médias formarão uma curva em forma de sino (uma distribuição normal), independentemente da aparência dos dados originais. 

Ambos são importantes na estatística, mas descrevem coisas diferentes: um se concentra na precisão e o outro na forma.

Principais conclusões

A lei dos grandes números destaca um princípio fundamental na análise de dados: amostras maiores fornecem resultados mais estáveis e precisos, mas somente quando os dados são representativos. 

Embora grandes conjuntos de dados reduzam os efeitos da variação aleatória, mais dados nem sempre são melhores. Se os dados forem tendenciosos ou desequilibrados, até mesmo um conjunto de dados enorme pode produzir resultados enganosos. Para tirar conclusões válidas, você precisa tanto de volume quanto de qualidade.

Se você quiser construir uma base mais sólida sobre esses conceitos, o curso Statistical Thinking in Python é um ótimo lugar para começar. A partir daí, explore a distribuição gaussiana para entender como a lei dos grandes números se conecta a outras ferramentas importantes em estatística e machine learning.