DeepSeek mHC explicado: Dimensionando LLMs além dos FLOPs

mHC (Hiperconexões com restrições múltiplas) resolve um problema que a maioria das equipes enfrenta ao escalar LLMs: você pode continuar adicionando GPUs, mas, em algum momento, o treinamento fica instável e o rendimento para de melhorar.

Aqui está a ideia principal:

• Em grande escala, os limites reais geralmente são a largura de banda da memória, a comunicação entre GPUs e a sobrecarga de latência.
• As hiperconexões (HC) tentam melhorar a capacidade do modelo, deixando as informações fluírem por caminhos residuais mais ricos, sem aumentar muito os FLOPs por camada. Mas essa mistura extra pode quebrar o “atalho de identidade” que tornava as redes residuais estáveis em primeiro lugar, fazendo com que o treinamento fosse por água abaixo.
• O mHC resolve isso limitando como esses caminhos residuais se misturam. A mistura residual é forçada a se comportar como uma média ponderada bem comportada (uma matriz duplamente estocástica, aplicada usando Sinkhorn–Knopp), o que evita que os sinais e gradientes explodam ou desapareçam.

As hiperconexões melhoram a conectividade e a capacidade, mas as hiperconexões com restrições múltiplas (mHCs) tornam essa atualização estável e escalável, sem ignorar os verdadeiros gargalos, como largura de banda de memória e comunicação.

Se você quiser saber mais sobre alguns dos princípios abordados neste tutorial, recomendo dar uma olhada no curso Modelos Transformadores com PyTorch e o curso Deep Learning com PyTorch.

O que é mHC? De conexões residuais a hiperconexões

Nesta seção, vou explicar a necessidade de ir além das conexões residuais simples, como o HC tentou resolver isso e por que o mHC é a solução que faz a ideia funcionar em escala LLM.

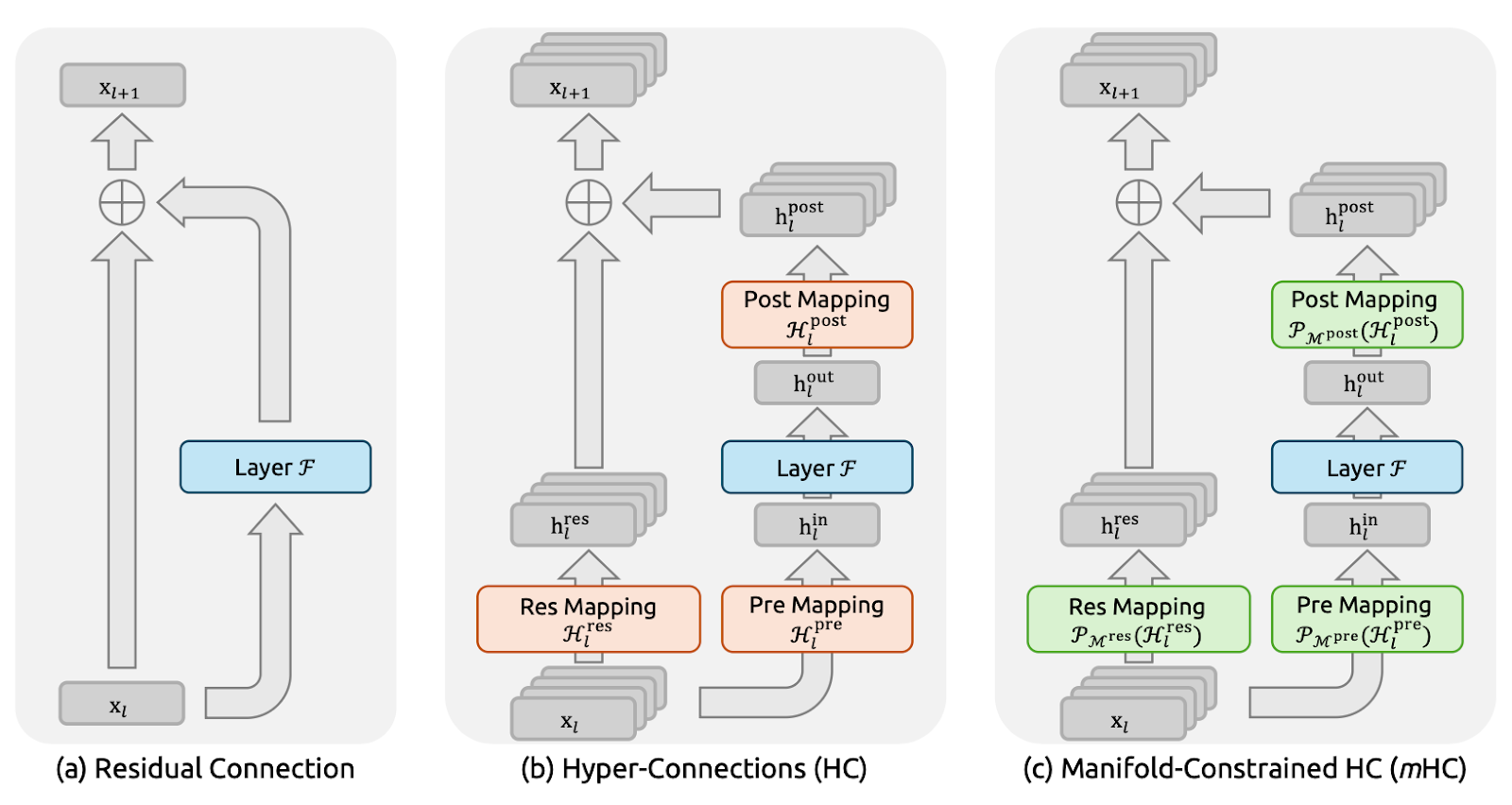
Figura 1: Ilustrações de paradigmas de conexão residual (artigo sobre mHC)

As conexões residuais (Figura a) fornecem a cada camada um atalho de identidade, permitindo que sinais e gradientes fluam de forma limpa através de redes muito profundas. 

O DeepSeek usou explicitamente esse princípio de mapeamento de identidade como ponto de partida para o artigo sobre mHC. A desvantagem é que um caminho residual simples também é muito restritivo, então não permite muita troca de informações dentro do fluxo residual. 

Enquanto as Hiperconexões (HC) (Figura b) eram o próximo passo natural, que em vez de um fluxo residual, se expande em n fluxos paralelos e adiciona mapeamentos pré/pós/residuais aprendíveis para que os fluxos possam se misturar e compartilhar informações. Isso aumenta a expressividade sem necessariamente explodir os FLOPs por camada. 

Mas, em grande escala, o HC enfrenta dois grandes problemas. Primeiro, como os fluxos se misturam livremente em cada camada, essas pequenas misturas se acumulam à medida que você vai se aprofundando. Em várias camadas, a rede pode parar de funcionar como uma “conexão direta” limpa, e os sinais ou gradientes podem explodir ou desaparecer, deixando o treinamento instável. Segundo, mesmo que os cálculos extras sejam simples, o custo do hardware aumenta rapidamente.

As hiperconexões com restrições múltiplas (mHC) (Figura c) mantêm a conectividade extra das HC, mas tornam seguro treinar como uma ResNet. 

A ideia principal é que, em vez de deixar os fluxos residuais se misturarem de qualquer maneira, o mHC faz com que a mistura siga regras bem rígidas. No artigo, isso é feito transformando a matriz de mistura em uma “média ponderada” bem comportada, usando um procedimento chamado Sinkhorn–Knopp. O resultado é que, mesmo depois de muitas camadas, a mistura continua estável, e os sinais e gradientes não explodem nem desaparecem.

Resumindo, mudamos das conexões residuais para o mHC porque queríamos um fluxo de informações mais rico, em vez de um único caminho de salto.

Conceitos-chave do mHC

Em um nível mais alto, o mHC mantém a mistura multistream do Hyper-Connection, mas coloca proteções rígidas na mistura para que ela funcione como um caminho de salto estável, no estilo ResNet, mesmo quando empilhamos centenas de camadas. 

Os autores limitam a matriz de mistura residual Hlres​ para que ela se comporte bem em toda a profundidade, ao mesmo tempo que permite que os fluxos troquem informações.

Na prática, o mHC faz com que Hlres​​ seja duplamente estocástico, ou seja, todas as entradas são não negativas e cada linha e cada coluna somam 1. Isso faz com que o fluxo residual funcione como uma média ponderada controlada. 

Isso mostra que o mapeamento não é expansivo (norma espectral limitada por 1), fica estável quando multiplicado entre camadas (fechamento sob multiplicação) e tem uma mistura intuitiva como interpretação de mistura de média/permutação através do politopo de Birkhoff. Isso também faz com que os mapeamentos pré/pós sejam não negativos para evitar o cancelamento do sinal. 

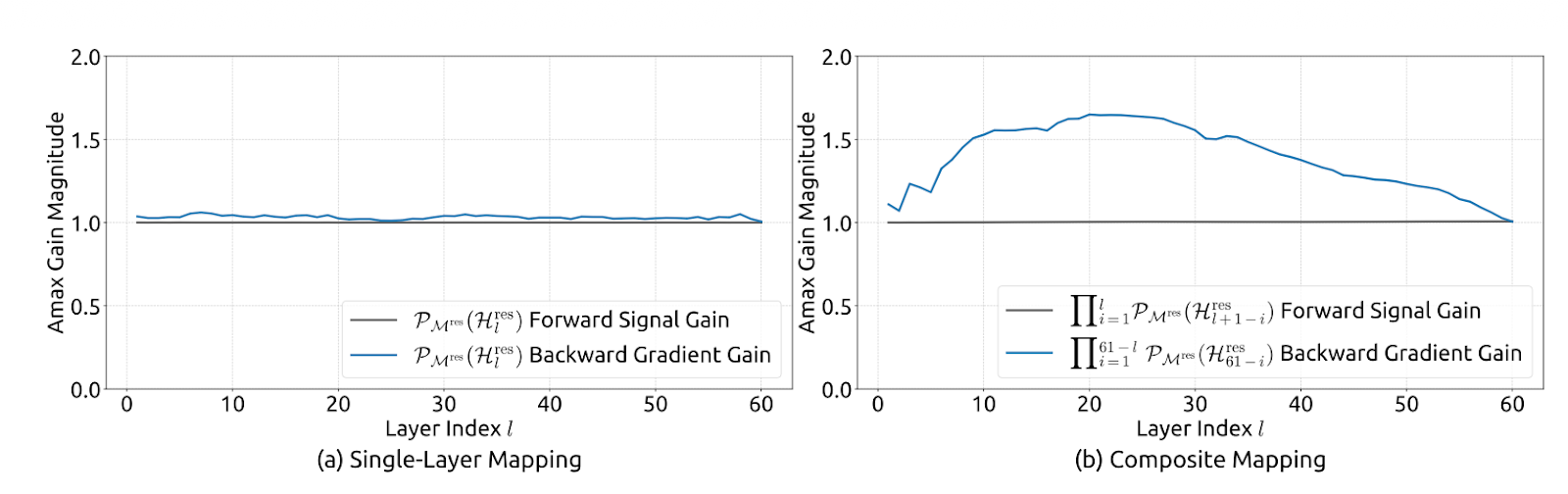
Figura 2: Estabilidade de propagação de hiperconexões com restrições múltiplas (artigo mHC)

Em termos de implementação, o artigo mantém a praticidade calculando mapeamentos brutos sem restrições Hlpre, Hlpost e Hlres a partir do estado multistream da camada atual (eles achatam xl para preservar o contexto completo) e, em seguida, projetam-nos nas formas restritas. Hlpre e Hlpost​​ são obtidos com uma restrição baseada em sigmoide, enquanto ​Hlres é projetado usando a exponenciação de Sinkhorn-Knopp para tornar as entradas positivas e, em seguida, alternar as normalizações de linha/coluna até que as somas sejam 1.

Os autores também relatam a implementação do mHC (com n=4) em escala com apenas ~6,7% de sobrecarga de tempo de treinamento, principalmente por meio da redução agressiva do tráfego de memória. Eles reorganizaram as partes do RMSNorm para aumentar a eficiência, usaram fusão de kernel (incluindo a implementação de iterações Sinkhorn dentro de um único kernel com um backward personalizado), fundiram a aplicação de Hlpost​​ e Hlres com fusão residual para reduzir leituras/gravações, usaram recálculo seletivo para evitar o armazenamento de grandes ativações intermediárias e comunicação sobreposta em uma programação DualPipe estendida para ocultar a latência do estágio do pipeline.

Otimizando o mHC: Técnicas de Sistemas 

A estabilidade por si só não é suficiente. Se o mHC adicionar muito tráfego de memória ou comunicação entre GPUs, a gente perde em termos de rendimento. Então, os autores juntaram o método mHC com um conjunto de otimizações de infraestrutura feitas pra não sobrecarregar a memória.

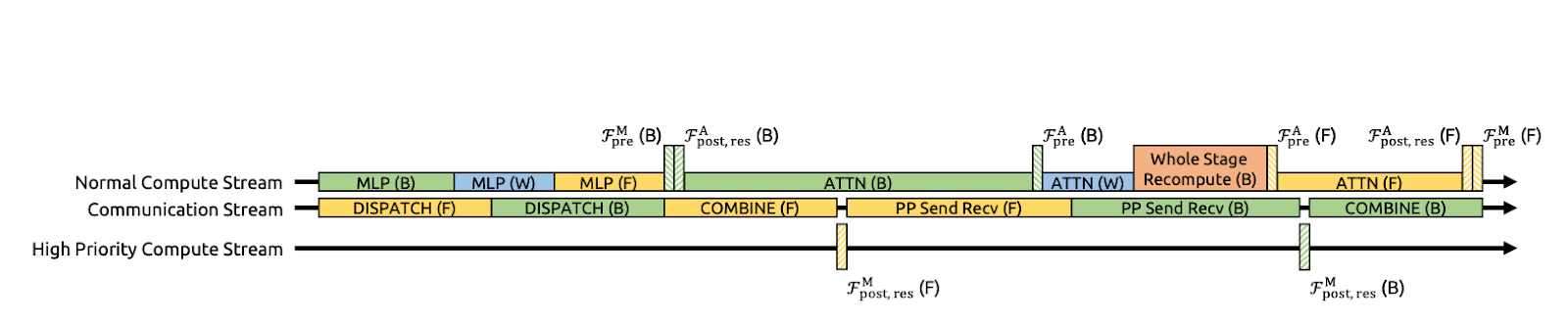
Figura 3: Sobreposição de comunicação-computação para mHC (artigo sobre mHC)

Fusão do kernel para reduzir leituras/gravações na memória

Os autores aceleram o mHC juntando várias etapas em um único kernel da GPU. Em vez de aplicar Hlpost​, Hlres e, em seguida, mesclar de volta ao fluxo residual como passagens separadas (o que força a GPU a gravar tensores intermediários na memória e lê-los de volta), eles fazem essas operações em uma única passagem. 

Isso reduz bastante o tráfego de memória. Agora, o kernel lê valores de (n+1)C em vez de (3n+1)C e grava valores de nC em vez de 3nC. Aqui, C é o tamanho oculto (características por fluxo) e n é o número de fluxos residuais, então nC é o tamanho do estado residual ampliado. Menos leituras/gravações significam menos dados indo e vindo da memória. 

O artigo também sugere implementar a maioria dos kernels usando TileLang para aproveitar melhor a largura de banda da memória. 

Recálculo para controlar a memória de ativação

O mHC multistream aumenta a quantidade de ativações intermediárias que você normalmente teria que armazenar para o backprop, o que pode esgotar a memória da GPU e forçar lotes menores ou checkpoints mais agressivos. 

Para evitar isso, o artigo sugere um truque simples: não armazene os intermediários mHC após a passagem direta. Em vez disso, recalcule os kernels mHC leves durante a passagem para trás, pulando o recálculo da camada Transformer F, que é cara. 

Isso reduz a pressão sobre a memória e ajuda a manter um rendimento efetivo mais alto. Uma limitação prática é que esses blocos de recálculo devem se alinhar com os limites das etapas do pipeline; caso contrário, o agendamento do pipeline fica confuso.

Agendamento com reconhecimento de comunicação com sobreposição DualPipe

Em grande escala, o paralelismo do pipeline é comum, mas o design n-stream do mHC aumenta a quantidade de dados que precisam passar por várias etapas, o que pode causar atrasos perceptíveis na comunicação. 

O DeepSeek otimiza isso estendendo o DualPipe para que a comunicação e a computação se sobreponham nos limites do pipeline. Isso quer dizer que as GPUs fazem um trabalho útil enquanto as transferências rolam, em vez de ficarem paradas esperando o envio/recebimento terminar. Eles também rodam alguns kernels em um fluxo de computação de alta prioridade, para que a computação não bloqueie o progresso da comunicação. O resultado é que o custo extra de comunicação do mHC fica meio escondido, melhorando a eficiência do treinamento de ponta a ponta.

Pontos de interesse 

Mesmo que não implementemos o mHC, a estrutura do DeepSeek é uma boa maneira de identificar onde o sistema está realmente perdendo tempo.

• Cargas de trabalho de contexto longo: Prompts longos tornam o preenchimento prévio caro, porque a atenção precisa mover muitos dados pela memória. Durante a decodificação, o cache KV continua a crescer, o que aumenta as leituras de memória por token. Juntos, eles aumentam os limites da largura de banda da memória e muitas vezes causam fragmentação ou processamento em lote ineficiente.
• Roteamento MoE e paralelismo especializado: Com o Mixture of Experts (MoE), o custo não é só sobre computação. É o roteamento, a troca de tokens e a comunicação entre GPUs necessárias para enviar tokens aos especialistas e reunir os resultados. A sobreposição DualPipe do DeepSeek foca em esconder a comunicação do pipeline por trás da computação, que o MoE precisa em grande escala.
• Tráfego multi-tenant e em pequenos lotes: Em implementações reais, as solicitações não chegam em grandes lotes organizados. A gente acaba com lotes menores e inconsistentes, comprimentos de sequência misturados e reutilização de cache mais fraca. Isso prejudica a eficiência do processamento em lote e aumenta a latência da cauda, de modo que a largura de banda da memória e o agendamento se tornam o gargalo.

Cache KV e tráfego de memória

Mesmo que o mHC seja principalmente uma ideia de treinamento, a lição principal do artigo se aplica diretamente à inferência. O artigo foca em otimizar não só os FLOPs, mas também o tráfego de memória, a comunicação e a latência. A maior prova é a decodificação de contexto longo, onde a estimativa aproximada do cache KV é:

KV_bytes ≈  2 x L x T x H x bytes_per_elem x batch

Para FP16/BF16, o valor de bytes_per_elem é 2. Por exemplo, com um formato típico (L=32, H=4096, batch=1), 8K tokens equivalem a ~4 GB de KV, enquanto 128K tokens equivalem a ~64 GB, então mesmo que a computação continue razoável, a memória ainda pode explodir e você fica limitado pela largura de banda. 

É por isso que as otimizações práticas de inferência se concentram em reduzir o movimento da memória usando técnicas como quantização de cache KV, KV paginado e evicção, kernels de atenção eficientes (família FlashAttention), agrupamento contínuo e bucketing de forma, e paralelismo sensível à comunicação. 

O objetivo é manter os ganhos de desempenho sem pagar um imposto oculto em leituras/gravações de memória e sincronização.

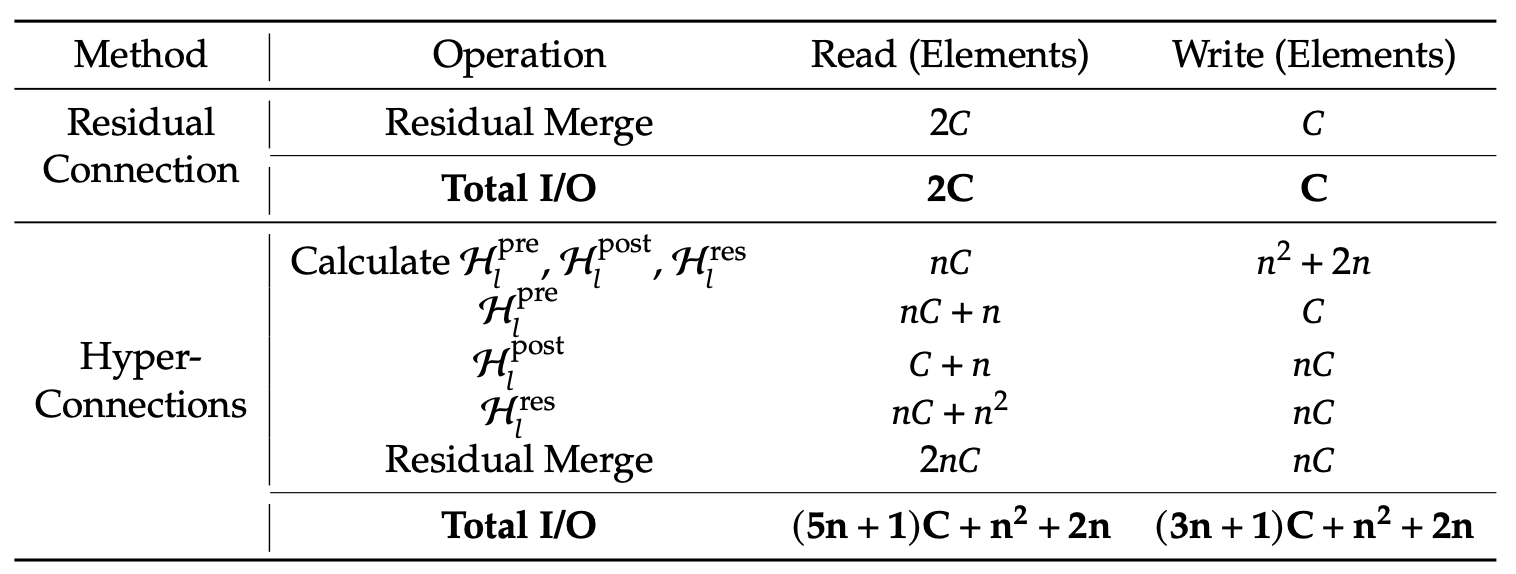
Tabela 1: Comparação dos custos de acesso à memória por token (artigo sobre mHC)

A DeepSeek relata que o mHC tem um desempenho consistentemente superior à linha de base e supera o HC na maioria dos benchmarks para modelos 27B, incluindo +2,1% no BBH e +2,3% no DROP em comparação com o HC. Isso mostra que o mHC traz resultados melhores em grande escala.

Conclusão

A principal lição deste artigo é que escalar LLMs não é só um problema de FLOPs; é também um problema de estabilidade e sistemas. As hiperconexões (HC) aumentam a capacidade do modelo ao expandir o fluxo residual e permitir que vários fluxos se misturem, mas em grandes profundidades, essa mistura se transforma em um mapeamento composto que pode se desviar significativamente de um caminho de identidade, levando à explosão ou desaparecimento do sinal/gradiente e a falhas no treinamento.

O mHC resolve isso colocando barreiras nessa mistura, limitando a matriz de mistura residual para ser duplamente estocástica (não negativa, soma das linhas/colunas igual a 1), aplicada via Sinkhorn–Knopp, de modo que o caminho residual se comporta como uma média ponderada controlada e permanece estável mesmo quando você empilha muitas camadas.

O DeepSeek também considera a eficiência de tempo de execução como parte do método. Eles usaram fusão de kernel para reduzir as leituras/gravações de memória de alta largura de banda e recálculo seletivo para minimizar a memória de ativação. 

Além disso, eles ampliaram o DualPipe para sobrepor a comunicação com a computação, garantindo que as paralisações do pipeline não apaguem os ganhos. O resultado não é só um treinamento mais estável, mas também um desempenho melhor a jusante em escala.

Se você quiser saber mais sobre desenvolvimento de aplicativos LLM, recomendo dar uma olhada no curso curso Desenvolvimento de Aplicativos LLM com LangChain.