Vetores e valores próprios: Principais percepções para a ciência de dados

Os vetores e valores próprios são conceitos fundamentais da álgebra linear que têm implicações de longo alcance na ciência de dados e no aprendizado de máquina. Essas entidades matemáticas fornecem informações valiosas sobre o comportamento das transformações lineares, o que nos permite entender a estrutura subjacente dos dados, simplificar conjuntos de dados complexos com um grande número de recursos e, portanto, permitir que seu processamento atinja o objetivo desejado.

Se isso soa como redução de dimensionalidade para você, você está certo. Os autovetores e os autovalores funcionam nos bastidores de muitas técnicas de redução de dimensionalidade, como a análise de componentes principais (PCA). Eles também são as engrenagens para o agrupamento espectral, que envolve a redução da dimensionalidade como uma etapa inicial.

Para entender o conceito de mundo próprio, você precisaria ter uma boa compreensão dos conceitos anteriores de álgebra linear, principalmente vetores e escalares, transformação linear e determinantes. Se você não conhece esses conceitos, pode fazer nosso curso prático de Álgebra Linear para Ciência de Dados em R ou, se for usuário de Python, pode ver este tutorial do SciPy sobre vetores e matrizes.

O que são vetores próprios e valores próprios?

Vamos começar pelo fato de que a parte "eigen" dos vetores e valores próprios tem um significado e não é o nome de alguém que os inventou. Eigen é uma palavra alemã que pode ser traduzida aproximadamente neste contexto como "característica" ou "característica intrínseca" de algo.

Agora, imagine que submetemos um grupo de vetores a uma transformação linear, como escala, cisalhamento ou rotação. Alguns vetores mudam de direção, e outros não. Os vetores que não mudam de direção (ou giram exatamente na direção oposta) são o que chamamos de vetores próprios, pois eles se tornam os vetores "característicos" da transformação que ocorreu (ou da matriz que descrevem). A quantidade (magnitude) que foi dimensionada é o valor próprio. Ou seja, o valor próprio é o fator de escala da transformação.

Compreensão de vetores e valores próprios

Para entender melhor os conceitos dos dois, vamos analisar um caso geométrico e, em seguida, passar para a aplicação deles na ciência de dados.

Interpretação geométrica

Imagine um espaço bidimensional, no qual temos três vetores, um azul que fica no eixo x, um vermelho que fica no eixo y e um verde que fica na diagonal entre os dois. Agora, aplicamos uma transformação de escala ao longo do eixo y com um fator de dois, conforme mostrado nas imagens abaixo.

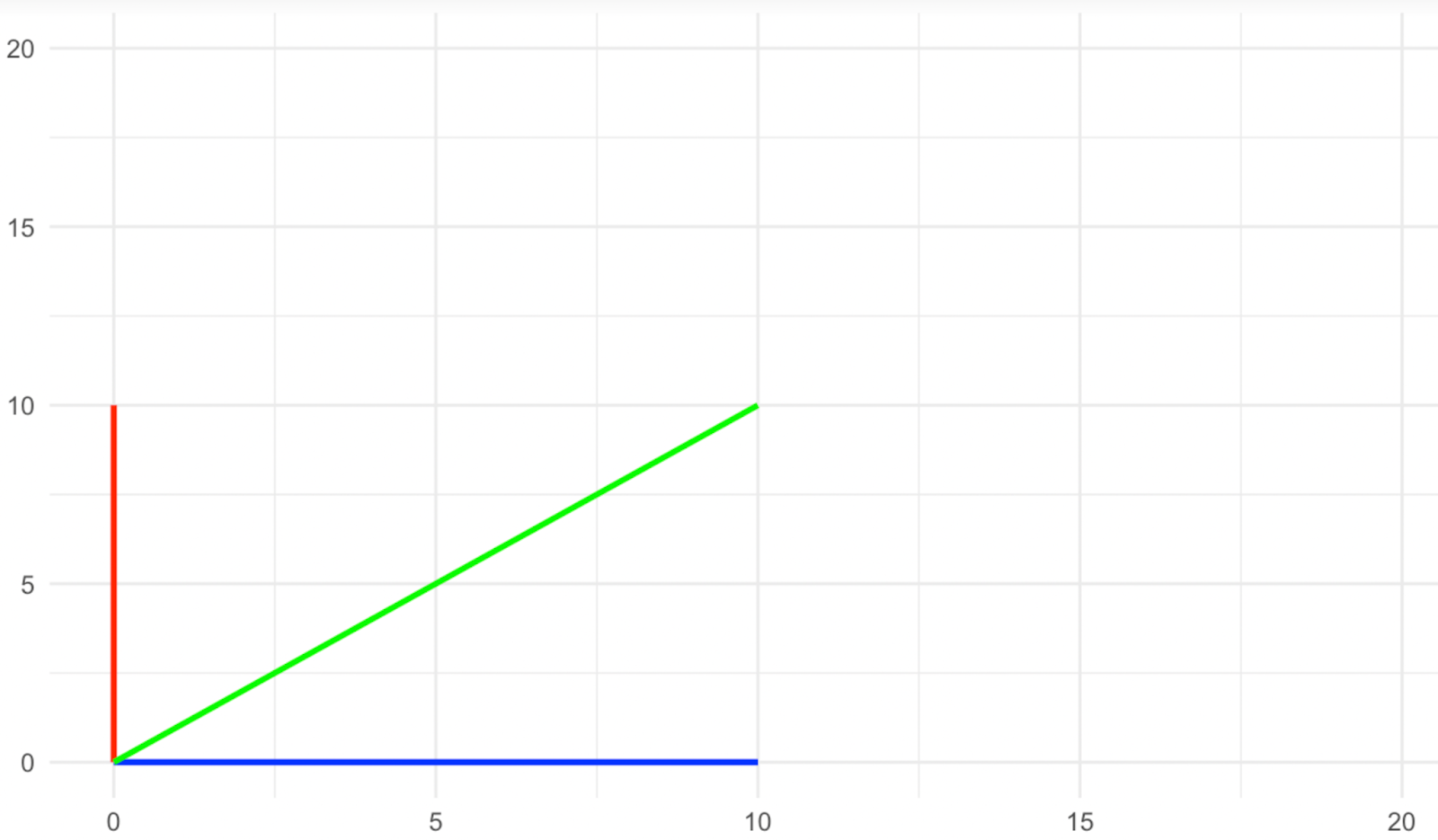
Vetores antes do alongamento. Imagem do autor

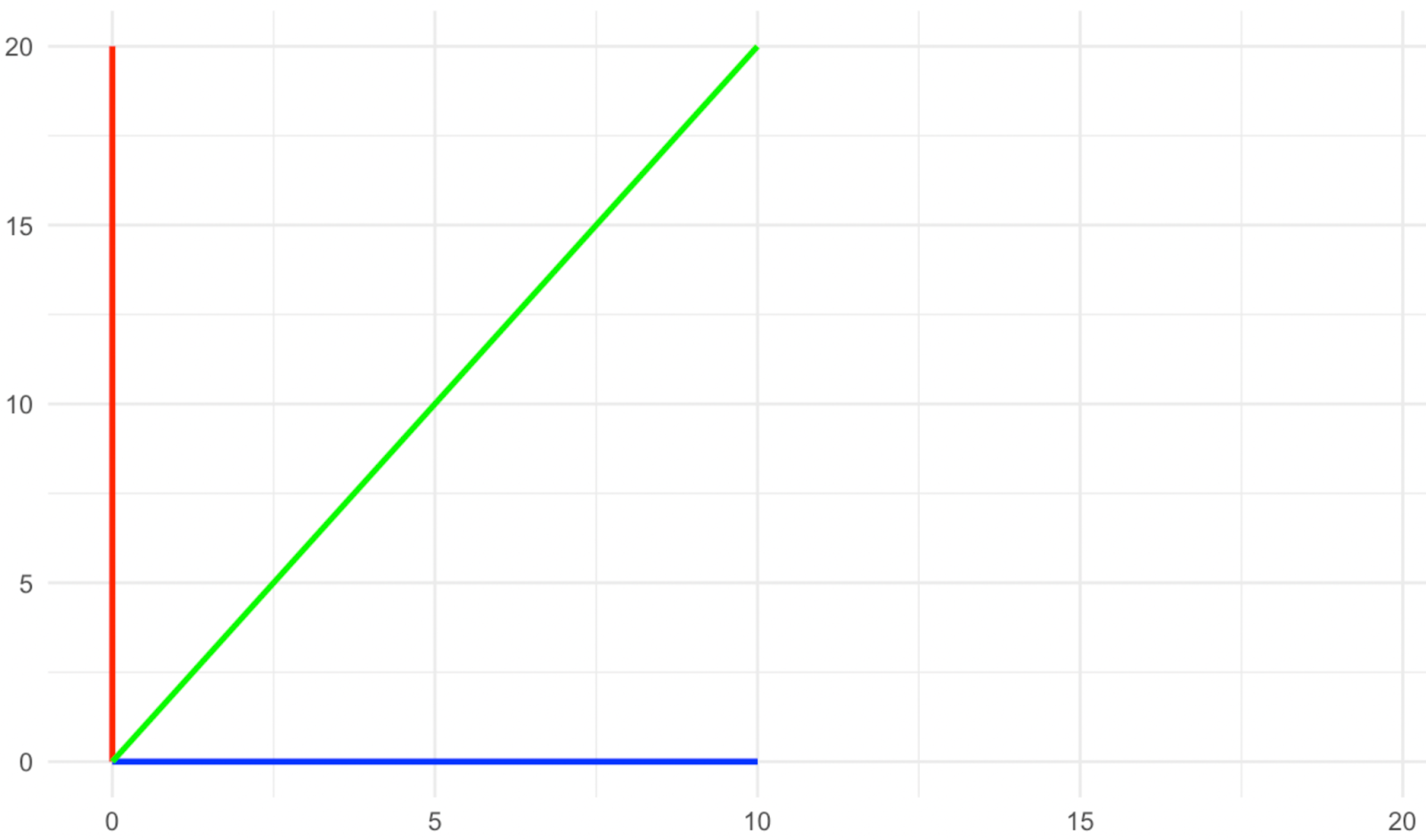
Vetores após o alongamento. Imagem do autor

O que aconteceu com os vetores de direção? As vermelhas e azuis não mudaram sua direção com a escala, enquanto a verde mudou sua direção, certo? Portanto, nesse tipo de transformação, os vetores vermelho e azul são o que chamamos de vetores próprios, pois eles se tornam os vetores característicos da transformação.

Dê uma olhada novamente nas imagens acima e veja o que aconteceu com a magnitude dos vetores próprios (os vermelhos e os azuis). O vetor próprio azul não alterou sua magnitude, enquanto o vermelho dobrou ou, em uma maneira elegante de dizer, foi dimensionado para o fator de dois. O valor pelo qual cada um dos vetores próprios foi dimensionado com a transformação é o que chamamos de valores próprios. Portanto, o valor próprio do vetor próprio azul aqui é 1 (pense nisso como uma multiplicação), enquanto o valor próprio do vetor próprio vermelho é 2, pois sua magnitude foi duplicada.

Propriedades dos valores próprios

Considere a transformação mostrada nas imagens abaixo e, antes de tudo, pense em quais são os vetores próprios nesse caso. Se você disse que são os três vetores, o vermelho, o verde e o amarelo, você está certo, pois todos eles apontam na direção exatamente oposta após a transformação. Vemos que o sinal do número (o valor próprio) pode nos fornecer informações adicionais sobre a transformação que ocorreu. Um valor próprio positivo indica que a transformação não incluiu uma rotação, enquanto um valor próprio negativo indica que a transformação incluiu uma rotação do vetor próprio em torno de sua origem.

Vetores antes da rotação. Imagem do autor

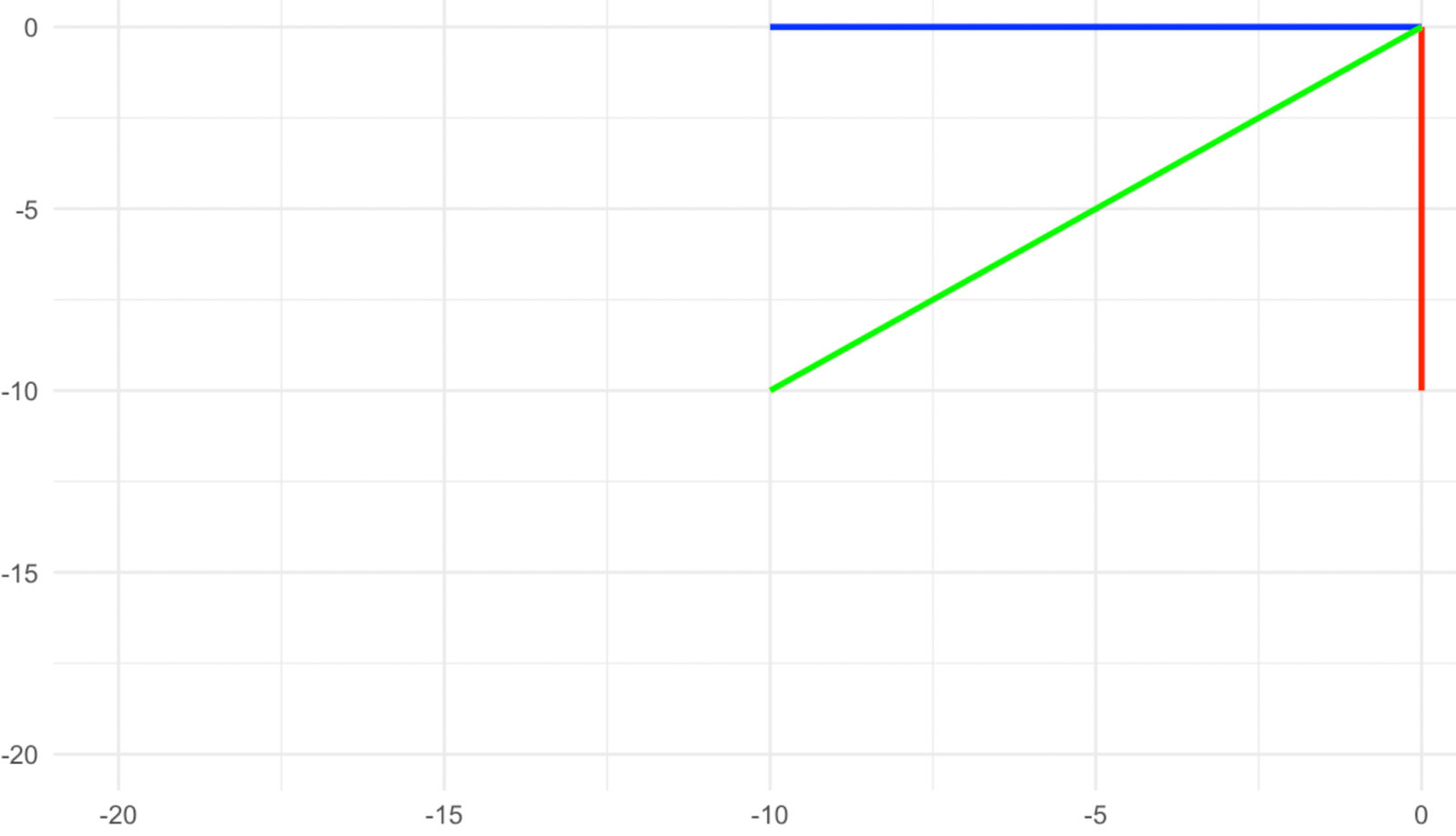
Vetores após a rotação. Imagem do autor

Agora, qual é o valor próprio de cada um desses vetores próprios? O fato de sua magnitude permanecer a mesma significa que o valor próprio é 1, mas o fato de que eles também giraram significa que o sinal de 1 deve ser negativo. Portanto, o valor próprio nesse caso é -1.

Em nosso exemplo, os valores próprios são simples (todos são 1), mas os valores próprios podem ser qualquer número, seja um número inteiro, como 1 e 2, ou um racional (fração), como ½ e 0,75. Eles podem ser o que chamamos de números irracionais, como o valor de π. Os valores próprios podem até ser números complexos, como a + bi, em que "a" e "b" são números reais separados e "i" é uma unidade imaginária, como a raiz quadrada de -1. Os valores próprios complexos também podem indicar o tipo de transformação linear que ocorreu, seja uma rotação ou uma transformação mais complexa, como uma oscilação.

Como calcular vetores próprios e valores próprios

Embora as bibliotecas do pacote básico do R e as bibliotecas do Python, como SciPy e NumPy, possam encontrar facilmente vetores e valores próprios, é extremamente importante entender as equações por trás deles. Nesta seção, vamos analisar o que chamamos de equação característica, que calcula passo a passo os vetores e valores próprios de uma matriz simples. Em seguida, mencionaremos outros métodos de computação matemática para matrizes maiores (ou seja, grandes conjuntos de dados).

Equação característica

Podemos encontrar os vetores e valores próprios usando o que é conhecido como equação característica. Usando a equação característica, os valores próprios são encontrados primeiro, antes dos vetores próprios. Quando o valor próprio é conhecido, ele é usado para calcular o vetor próprio correspondente, resolvendo um sistema de equações lineares. 

Etapa 1: Comece com a equação de transformação da matriz

Para uma matriz 𝐴 e um vetor 𝑣a equação básica para vetores próprios e valores próprios é:

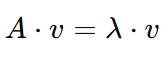
Isso significa que, quando a matriz 𝐴 atua sobre o vetor 𝑣, o resultado é uma versão em escala de 𝑣. Aqui:

• 𝐴 é uma matriz (uma grade quadrada de números).
• 𝑣 é o vetor próprio
• λ (lambda) é o valor próprio.

Lembre-se de que o objetivo é encontrar ambos λ (o valor próprio) e 𝑣 (o vetor próprio).

Etapa 2: Reorganize a equação

Para prosseguir com nosso objetivo, precisamos resolver o problema de λ. Portanto, primeiro reorganizaremos a equação para facilitar o trabalho, movendo o lado direito para o lado esquerdo com um sinal inverso:

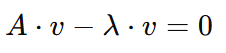
Agora podemos fatorar o 𝑣, mas como 𝐴 é uma matriz e 𝑣 é um vetor, precisaremos multiplicar 𝑣 pelo que chamamos de matriz identidade, denotada como I. Uma matriz identidade é uma matriz quadrada (com tamanho nxn) com 1 em sua diagonal e 0 em outros lugares. Devido à característica da multiplicação de matrizes, uma matriz identidade funciona como o número 1 para matrizes. Veja, por exemplo, essa matriz de identidade de tamanho 3x3:

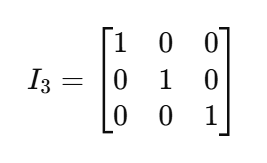
De volta à nossa equação, se você considerar o 𝑣e o multiplicarmos por Io resultado seria o seguinte:

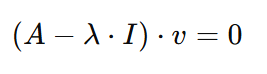
Etapa 3: Configure o determinante

Para resolver a equação a que chegamos, ou o vetor próprio 𝑣 deve ser zero, ou então o vetor próprio seria igual ao que quer que seja 𝐴-λ⋅I. E agora é o momento adequado para dizer mais uma coisa sobre os vetores próprios - eles não podem ser iguais a zero. Portanto, 𝐴-λ⋅I deve ser igual a zero. Mas como lambda é a incógnita, podemos fazer com que o lado esquerdo da equação seja igual ao lado direito se tomarmos o determinante do 𝐴-λ⋅I. Assim, chegamos à seguinte equação:

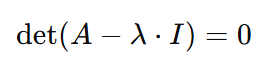
Aqui chegamos à equação característica. A solução da equação característica pode nos fornecer os valores próprios λ e o vetor próprio 𝑣, e é mostrada nas etapas restantes.

Etapa 4: Resolva os valores próprios

Supondo que você tenha a seguinte matriz 𝐴:

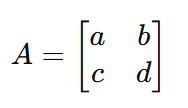
Ao substituir 𝐴 com a matriz real na equação característica, a equação se torna:

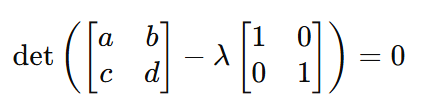
E, portanto:

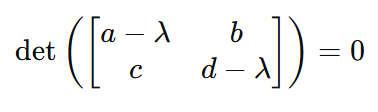
E, portanto, mais uma vez:

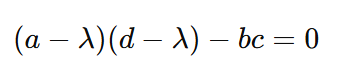
A partir dessa forma muito mais simples de equação, podemos calcular os valores dos valores próprios λ substituindo apenas os valores da matriz.

Etapa 5: Resolva os vetores próprios 𝑣

Ao obter os valores próprios λ, o que resta é obter os vetores próprios 𝑣. Você pode fazer isso voltando à forma anterior da equação:

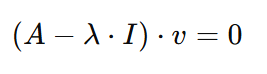
Agora, se substituirmos 𝐴, λe I com seus valores, podemos calcular facilmente o valor do vetor próprio 𝑣.

Métodos de computação numérica

Como vimos, a complexidade do cálculo dos vetores e valores próprios depende muito do tamanho da matriz. Em nosso exemplo, usamos uma matriz simples 2x2 𝐴. Mas, na prática, não é possível encontrar os vetores e valores próprios dessa forma quando as matrizes ficam muito maiores, como quando têm centenas ou milhares de linhas e colunas. Nesse caso, usamos linguagens de programação como Python e R, que usam métodos de computação numérica em vez de métodos simbólicos. Algumas das técnicas usadas incluem:

1. Algoritmo QR: Esse é um método comum para encontrar valores próprios. Ele envolve uma sequência de fatorizações de matriz(fatorizações QR) para convergir iterativamente para os valores próprios.
2. Decomposição de Cholesky ou LU: Para determinados tipos de matrizes (por exemplo, matrizes simétricas ou definidas positivamente), métodos especializados, como a decomposição de Cholesky ou LU, podem ser usados para um cálculo mais eficiente.
3. Balanceamento e dimensionamento: Para melhorar a estabilidade numérica, o R e o Python geralmente dimensionam e equilibram as matrizes antes de realizar os cálculos.

Considerações sobre ciência de dados e aprendizado de máquina

Os vetores e valores próprios são essenciais em muitas aplicações, incluindo as seguintes:

• Processamento de imagens: Eles são usados no reconhecimento facial e na classificação de imagens.
• Processamento de linguagem natural (NLP): Os vetores e valores próprios são usados na modelagem de tópicos e na incorporação de palavras.
• Sistemas de recomendação: Como na filtragem colaborativa e baseada em conteúdo, em que a redução da dimensionalidade pode melhorar a precisão dos sistemas de recomendação.
• Agrupamento espectral: Os vetores e valores próprios também são um componente fundamental do agrupamento espectral, que é um método que agrupa pontos de dados observando suas conexões em um gráfico, usando informações da estrutura dos dados em vez de apenas a distância, que tem várias aplicações práticas, como no processamento de imagens.
• Análise de componentes principais: A PCA é uma técnica de redução de dimensionalidade comum no aprendizado de máquina. Com a PCA, você encontra os vetores próprios da matriz de covariância padronizada e os classifica por valor próprio. 

Dissemos que os valores próprios podem ser qualquer número real ou complexo. Isso significa que o valor próprio pode ser zero e também pode significar que podemos ter vários valores próprios iguais na matriz analisada. Esses dois casos são considerados dois erros que podem surgir em qualquer análise de eigen. Vamos dar uma olhada em cada um deles.

Problema de valor próprio zero

Um valor próprio zero é um problema porque significa que a transformação de seu vetor próprio correspondente resultou em um vetor zero, que pode ser imaginado como um único ponto no espaço sem magnitude e, portanto, não explica nenhuma variação no conjunto de dados. O problema pode ser tratado com técnicas de regularização, como a regressão de cumeeira (regularização de Tikhonov), ou com a remoção de recursos colineares (também conhecida como redução de dimensionalidade), o que acontece naturalmente em um algoritmo PCA. Portanto, o valor próprio zero não é um problema para a PCA e, de fato, a PCA pode ser uma solução para ele. No entanto, para outros algoritmos de aprendizado de máquina que envolvem a solução de sistemas lineares, como regressões lineares, de cumeeira e de laço, o problema do valor próprio zero deve ser tratado com antecedência.

Valores próprios degenerados

Quando vários valores próprios têm o mesmo valor, eles são chamados de degenerados e são um problema na ciência de dados, especialmente do ponto de vista prático em PCA e agrupamento espectral. Na PCA, se vários vetores próprios tiverem valores próprios idênticos, isso significa que esses vetores próprios capturam a mesma quantidade de variação no conjunto de dados e, portanto, a escolha de k componentes principais se torna problemática. No agrupamento espectral, em que os valores próprios da matriz de similaridade são usados para agrupar os pontos de dados, os valores próprios degenerados podem indicar que os pontos de dados são igualmente semelhantes em várias dimensões, o que dificulta a determinação de quais dimensões ou vetores próprios devem ser usados para separar os agrupamentos.

Vetores próprios, valores próprios e decomposição própria

Qualquer discussão sobre vetores e valores próprios não estaria completa sem que você falasse também sobre a decomposição de valores próprios. Eigendecomposição é o processo de decomposição de uma matriz quadrada A em seus vetores e valores próprios. Para uma matriz que pode ser decomposta, ela pode ser expressa como:

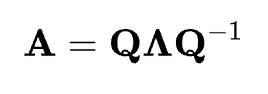
A decomposição de elementos nos diz que a matriz A pode ser expressa como o produto de sua matriz de vetores próprios Q, uma matriz diagonal Λ de seus valores próprios e o inverso da matriz de vetores próprios ^Q-1. Essas matrizes, quando multiplicadas juntas na multiplicação de matrizes, reconstruirão a matriz original A. A eigendecomposição é importante porque oferece uma maneira de entender e simplificar transformações lineares complexas, fornecendo insights sobre o comportamento do sistema, além de simplificar muitos cálculos. 

Conclusão

Neste artigo, vimos o que são vetores e valores próprios e como eles são extremamente relevantes para a ciência de dados e o aprendizado de máquina. Também vimos como eles são calculados matematicamente, bem como os erros que podem surgir ao tentar encontrar vetores e valores próprios.

Além do curso de Álgebra Linear em R e do tutorial SciPy sobre vetores e matrizes, se você leva a sério os autovetores e autovalores e suas aplicações em aprendizado de máquina, experimente nosso curso de carreira de Cientista de Aprendizado de Máquina com Python e torne-se um especialista em aprendizado supervisionado e não supervisionado, incluindo, é claro, a redução de dimensionalidade.