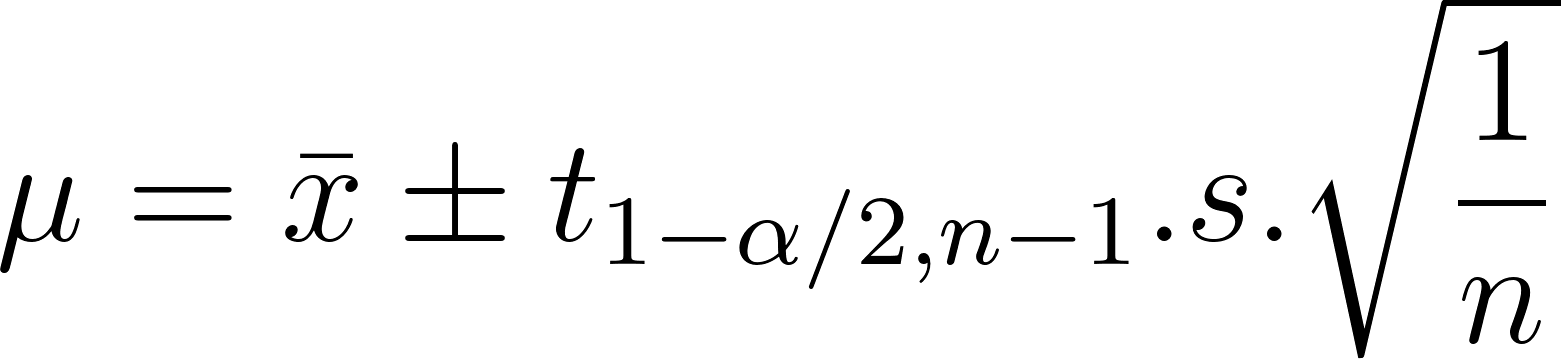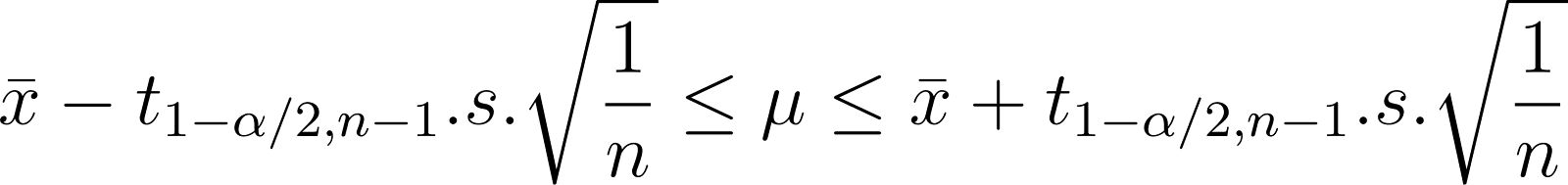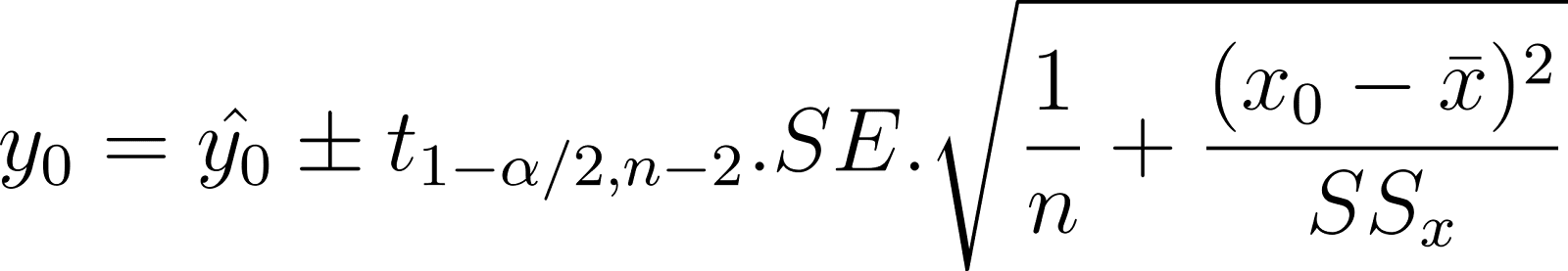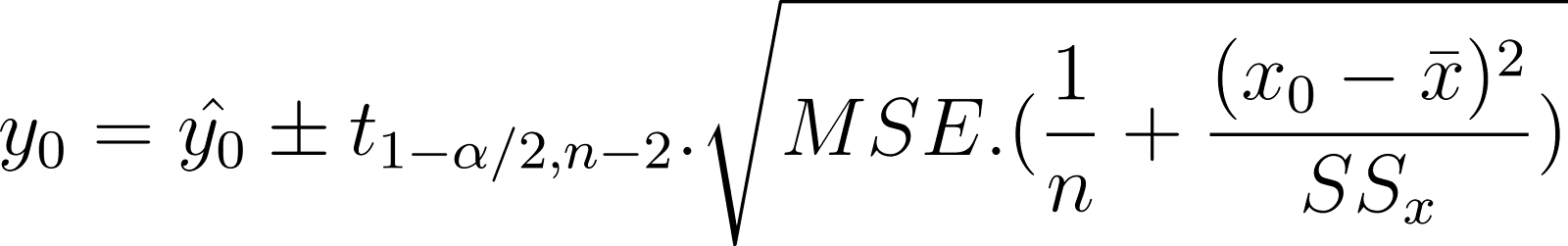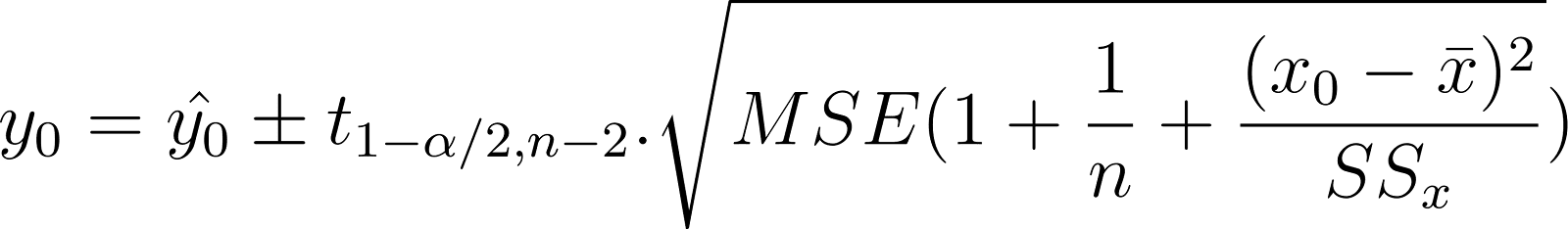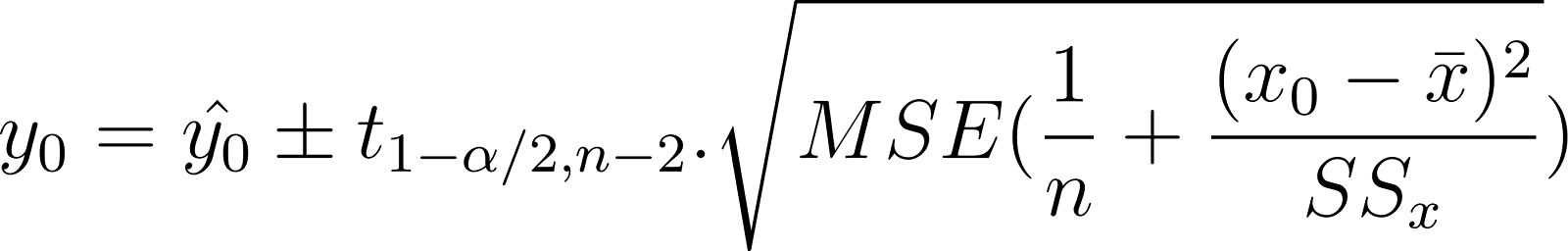Intervalos de confiança versus intervalos de previsão: Entendendo a diferença

Diferenças entre intervalos de previsão e intervalos de confiança

Os dois conceitos - intervalos de previsão e intervalos de confiança - estão intimamente relacionados. A mesma análise pode frequentemente envolver o uso de ambos os tipos de intervalos. Portanto, é útil compará-los frente a frente. 

Objetivo e interpretação

Quando você precisa conhecer um parâmetro populacional, como uma média, você usa uma amostra para estimar esse parâmetro. Como o tamanho da amostra é normalmente muito menor do que a população, a estimativa do parâmetro da amostra é imperfeita. O intervalo de confiança é o intervalo (da estimativa da amostra) que se espera que contenha o parâmetro da população. 

Os coeficientes de regressão também são considerados parâmetros populacionais. Como eles são estimados com base em uma amostra (e não em toda a população), alguns erros são incorporados a esses parâmetros. Assim, os coeficientes de regressão também podem ser expressos com um intervalo de confiança. 

Além disso, você pode usar a regressão para prever qualquer um deles:

• O valor médio de uma variável dependente (como o peso médio de cães de 2 anos de idade) ou
• O valor de um ponto de dados individual (como um cachorro individual de 2 anos de idade). 

O primeiro usa um intervalo de confiança, e o segundo usa um intervalo de previsão. A seção a seguir explica essa diferença em mais detalhes.

Cálculo e largura do intervalo

Cálculo do intervalo de confiança para inferência estatística 

Conforme explicado anteriormente, o intervalo de confiança é proporcional ao desvio padrão e inversamente proporcional ao tamanho da amostra. O intervalo de confiança da média da população, 𝛍, é expresso como:

Na expressão acima:

• x é a média da amostra, a estimativa, que você pode medir
• 𝛍 é a média da população, o parâmetro da população que você deseja estimar. 
• n é o tamanho da amostra
• s é o desvio padrão da amostra
• t é o valor crítico da distribuição T de Student em
• Nível de significância de 1 - α
• n-1 graus de liberdade
• Você pode encontrar os valores T em tabelas padronizadas - basta pesquisar no Google por "Student's T table". 

Assim, o intervalo de 𝛍 é:

Compreensão dos níveis de confiança e de significância 

Observe também que o tamanho do intervalo é proporcional ao valor t. Se você quiser um grau extremamente alto de confiança (certeza) de que o valor real está dentro de um determinado intervalo, esse intervalo deverá ser muito grande. Quanto menor for o grau de confiança, mais estreito será o intervalo. Porém, um grau de confiança muito baixo não é muito útil. Portanto, na prática, é comum escolher níveis de confiança de 90%, 95%, 99%, etc. 

Se você tem um nível de confiança de 95%, isso leva a um nível de significância de 5%. Supondo um intervalo bilateral, você precisa encontrar o valor crítico t em 2,5% (0,025). 

Conceitualmente, todos os intervalos são expressos da seguinte forma:

Observe que, em todos os casos, quanto maior o erro, maior o intervalo. Esse erro é calculado de forma diferente, dependendo do caso de uso. Para inferência, o erro é o desvio padrão. Para regressão, o erro é mostrado nas próximas seções. 

Cálculo do intervalo de confiança para regressão 

Ao prever o valor médio da variável dependente, você estima seu intervalo usando o intervalo de confiança. Por exemplo, você deseja prever um intervalo para o peso médio de cães de 2 anos de idade com base na idade deles. Isso é chamado de intervalo de confiança da resposta média. Ele também é considerado um parâmetro populacional porque é uma propriedade de toda a população. O intervalo é expresso como:

Na expressão acima:

• y0 é o valor real do parâmetro previsto.
• y0 é o valor previsto usando a relação de regressão.
• O valor t crítico foi explicado na seção anterior
• n é o tamanho da amostra
• (x0 -x) é a diferença entre o valor médio de x e x0para o qual você está tentando prever y0. Observe que quanto maior for essa diferença, maior será o intervalo. Assim, você obtém intervalos estreitos (e previsões mais precisas) para valores de xpróximos à média da amostra .
• SSx é o desvio ao quadrado da amostra de valores x. Ela é expressa como:

• SE é o erro padrão da estimativa. É a raiz quadrada do erro quadrático médio (MSE). O MSE é a variância do erro. Portanto, o SE é análogo ao desvio padrão do erro. O MSE é baseado no erro residual. Ela é expressa como: 

Na expressão acima, o termo de soma também é chamado de soma dos quadrados dos resíduos. O resíduo é a diferença entre o valor real de y e o valor previsto de y. 

Usando o MSE em vez do SE, o intervalo de confiança da resposta média também pode ser escrito como:

Compare a expressão acima com a relação conceitual mostrada anteriormente. 

Observe que o erro leva em conta:

• A diferença entre os valores reais e previstos de y.
• A diferença entre o valor médio de x e o valor de xopara o qual você deseja gerar a previsão
• A dispersão geral de x (em relação à sua média)

Cálculo do intervalo de previsão para regressão 

Para prever o valor exato de um ponto de dados individual (não a média), você estima seu intervalo usando o intervalo de previsão. Por exemplo, você deseja prever o intervalo para o peso real de um cão específico de 2 anos de idade com base na idade. Isso é chamado de intervalo de previsão e é expresso como:

Compare isso com o intervalo de confiança mostrado anteriormente:

Observe que as duas expressões são bastante semelhantes. A única diferença é o termo de erro adicional no intervalo de previsão. O intervalo de previsão tem um termo MSE adicional dentro da raiz quadrada do que o intervalo de confiança. Isso é para levar em conta a variabilidade dos valores y que você deseja prever. Isso faz com que o intervalo de previsão seja mais amplo do que o intervalo de confiança. 

O esboço abaixo mostra os intervalos de confiança e de previsão em relação à estimativa pontual (valor previsto).

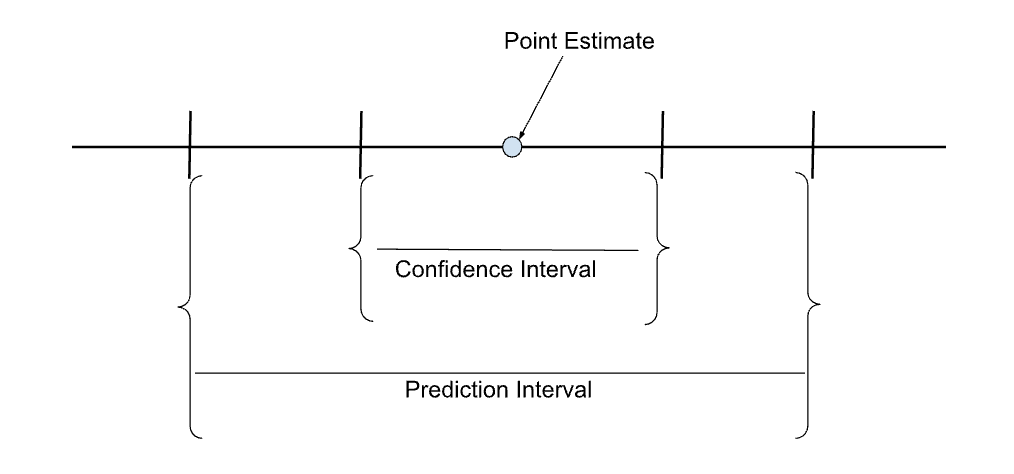
Comparação dos intervalos de confiança e de previsão de uma estimativa pontual. Imagem do autor.

O esboço esquemático abaixo mostra os intervalos de confiança e de previsão em relação à regressão - observe também que os intervalos são mais estreitos na região da média. 

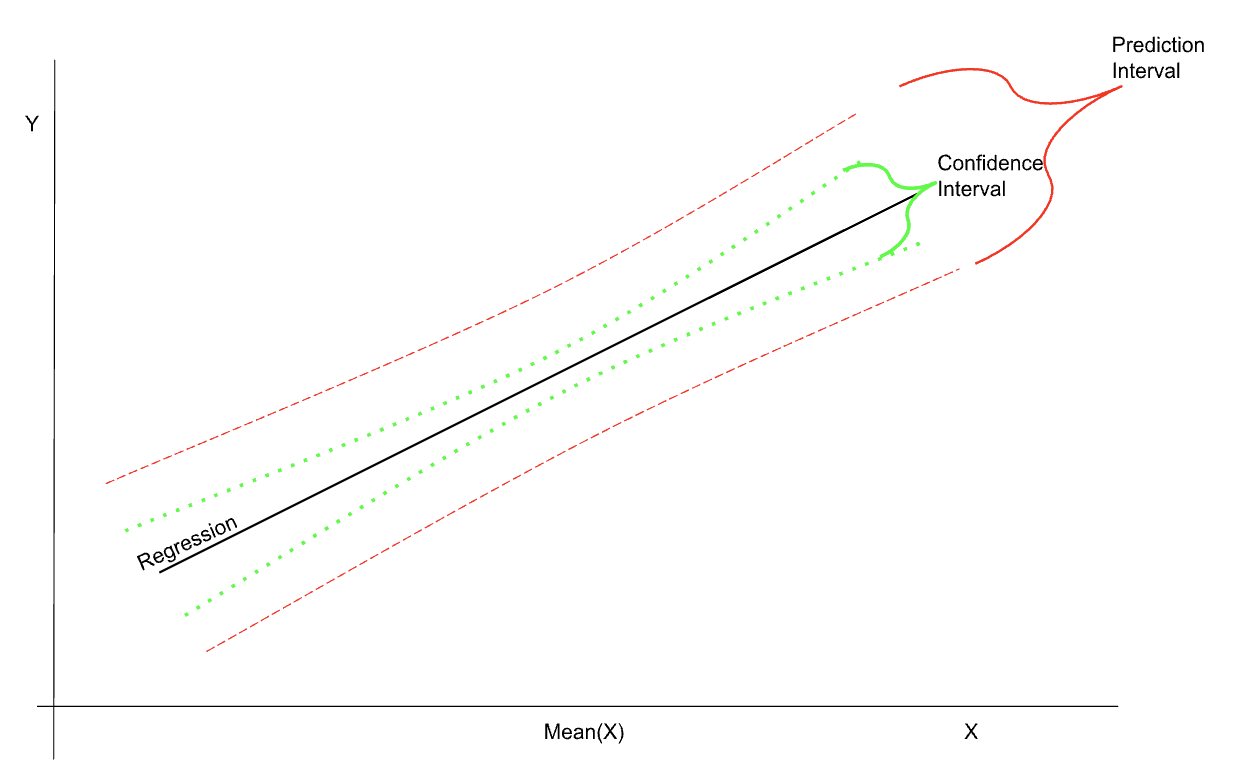
Ilustração dos intervalos de confiança e previsão na regressão. Imagem do autor.

Quando usar um intervalo de confiança

As seções anteriores discutiram os conceitos básicos de intervalos de confiança e de previsão, seus usos e as fórmulas usadas para calculá-los. Esta seção fornece exemplos práticos de quando usar intervalos de confiança e de previsão. 

Um intervalo de confiança é usado ao estimar um parâmetro populacional. Para estimar o parâmetro da população, você pode:

1. Use medições diretas com base em uma amostra aleatória
2. Use um modelo de regressão baseado em uma amostra aleatória

Alguns exemplos de casos de uso do intervalo de confiança são:

• Estimativa de um parâmetro populacional com base na medição de uma amostra aleatória. Por exemplo, para estimar a altura e o peso médios de recém-nascidos, você tira as medidas de uma amostra aleatória de recém-nascidos. 
• Estimativa do comportamento de uma população por meio do estudo de uma amostra aleatória. Esse caso de uso é comum em estudos clínicos, nos quais você tenta estimar os efeitos de um medicamento na população estudando seus efeitos em uma amostra aleatória. 
• Previsão da resposta média de uma variável dependente com base em uma análise de regressão feita em uma amostra aleatória. Por exemplo, você deseja prever o peso médio de filhotes de 55 dias com base em uma amostra de pesos de filhotes medidos a cada 15 dias. 
• Definição de limites de tolerância em processos de fabricação. Por exemplo, se uma máquina produz peças com um peso especificado, nem todas as peças têm exatamente o mesmo peso que a especificação. O peso de cada peça está dentro de um intervalo de confiança do peso especificado. Esse intervalo é o limite de tolerância. Todas as peças com pesos além dos limites de tolerância são rejeitadas. Espera-se que a máquina produza peças que estejam, em sua maioria, dentro do limite de tolerância. 
• Controle de qualidade. Suponha que você queira determinar se as peças produzidas por uma máquina estão dentro do limite de tolerância. Não é possível medir todas as peças. Você precisa confiar na coleta de amostras aleatórias, medindo-as e, em seguida, usando as estimativas da amostra para avaliar os parâmetros da população. 
• Teste de hipóteses. Os níveis de confiança e de significância são dois lados da mesma moeda. Nível de significância = 1 - Nível de confiança.  Um intervalo de confiança, com um nível de confiança especificado, inclui os pontos de dados para os quais a hipótese nula é verdadeira em um nível de significância de (1 - o nível de confiança especificado). 

Quando usar um intervalo de previsão

Os intervalos de previsão são usados sempre que você prevê o valor esperado de um ponto de dados individual com base em observações de (e análise de regressão em) uma amostra aleatória. 

Alguns exemplos práticos incluem: 

• Previsão do intervalo de um ponto de dados individual com base em uma análise de regressão. Como os pontos de dados individuais podem ter maior variabilidade (do que a média da amostra), você precisa de uma faixa mais ampla do intervalo de previsão. Por exemplo, você deseja prever o peso de um filhote individual de 55 dias com base em uma amostra aleatória de pesos de filhotes medidos a cada 15 dias. 
• Você pode usar as simulações de Monte Carlo para prever o valor de uma variável desconhecida. Como os métodos Monte Carlo são probabilísticos, você obtém um resultado ligeiramente diferente a cada vez que executa o modelo. Essas diferenças entre diferentes resultados são codificadas no Intervalo de Incerteza de Monte Carlo, que é conceitualmente semelhante a um intervalo de previsão. 
• Na regressão padrão, você constrói uma relação para prever o valor médio de um parâmetro. Na regressão quantílica, você cria modelos diferentes para prever cada quantil do parâmetro de destino. Isso também permite que você crie intervalos de previsão mais granulares. 
• Os modelos de aprendizado de máquina estão preocupados em prever o valor de um parâmetro desconhecido. Em geral, esses modelos são baseados em métodos estatísticos e, portanto, preveem o valor médio da quantidade desconhecida. Assim, o resultado do modelo inclui tanto o valor esperado (médio) quanto o intervalo de previsão. 
• Os modelos de aprendizagem profunda usam uma série de redes neurais para fazer previsões. Para avaliar a incerteza na saída, é comum eliminar aleatoriamente diferentes neurônios para estudar a variabilidade na saída. A variação dessas previsões é usada para construir o intervalo de previsão. 
• Na previsão de séries temporais, o objetivo é prever o valor de um observável em uma etapa de tempo futura. As previsões são baseadas em modelos estatísticos como o ARIMA, que realiza a auto-regressão em uma média móvel. Assim, ele prevê o valor esperado. Os valores reais observados estão contidos em um intervalo de previsão do valor esperado. Esse intervalo de previsão é calculado como uma função do desvio padrão. Por exemplo, para um nível de confiança de 95%, o intervalo de previsão está dentro de 1,96 desvios padrão do valor esperado. Além disso, as previsões em várias etapas, que envolvem um horizonte de previsão mais longo, também envolvem um intervalo de previsão maior. Para saber mais sobre séries temporais, consulte o curso DataCamp sobre análise de séries temporais. 

Intervalo de confiança versus intervalo de previsão: Um resumo

Os intervalos de confiança e os intervalos de previsão são usados com frequência no mesmo contexto, o que torna importante entender a diferença entre eles. 

Esta tabela resume as diferenças com base na discussão das seções anteriores:

Implementação de intervalos de confiança e intervalos de previsão no R

Esta seção mostra exemplos práticos de como usar a linguagem de programação R para estimar intervalos de confiança e previsão. O R é uma linguagem projetada para aplicativos estatísticos e vem com conjuntos de dados e funções estatísticas incorporados. 

Para saber mais sobre regressões usando o R, siga o tutorial do DataCamp sobre regressões lineares no R.

Os exemplos abaixo usam o conjunto de dados Orange incorporado. Esse conjunto de dados rastreia a circunferência (em milímetros) e a idade (em dias) das laranjeiras. Naturalmente, seria de se esperar que, quanto mais velha a árvore, maior seria sua circunferência. 

Implementação de intervalos de confiança no R

Os exemplos abaixo mostram como estimar intervalos de confiança para estatísticas resumidas e análises de regressão. 

Intervalo de confiança em estatísticas resumidas

Para obter o intervalo de confiança da média, execute o teste T padrão usando a função t.test() no conjunto de dados:

t.test(Orange$circumference)

O resultado é parecido com o exemplo abaixo:

t = 11.923, df = 34, p-value = 1.076e-13 
alternative hypothesis: true mean is not equal to 0 
95 percent confidence interval:
   96.10926 135.60502 
sample estimates: 
mean of x
   115.8571 

Ele fornece a você a estimativa média e o intervalo de confiança de 95%. Por padrão, a função T-Test usa um nível de confiança de 95%. Use o parâmetro conf.level para especificar um intervalo de confiança diferente, como 99%. 

> t.test(Orange$circumference, conf.level = 0.99)

Esse comando produz a seguinte saída:

t = 11.923, df = 34, p-value = 1.076e-13 
alternative hypothesis: true mean is not equal to 0
99 percent confidence interval:
   89.34458 142.36970 
sample estimates: 
mean of x
   115.8571 

Observe que a média estimada é a mesma em ambos os casos. No entanto, o intervalo precisa ser maior para que você tenha um nível de confiança mais alto. Com base nos dados, tenho 99% de certeza de que a média está entre 89,3 e 142,4, mas apenas 95% de certeza de que está entre 96,1 e 135,6. Para um parâmetro estimado a partir de uma determinada amostra, quanto mais estreito for o intervalo de confiança, menor será o nível de confiança. 

Intervalo de confiança na regressão 

Nas análises de regressão, você precisa dos intervalos de confiança para os coeficientes de regressão e valores previstos. 

Para que você entenda em profundidade como fazer regressões em R, siga o curso do DataCamp sobre Inferência para regressão linear em R.

Intervalo de confiança dos coeficientes de regressão 

Os coeficientes de regressão são estimados por meio da análise de uma amostra aleatória. Portanto, eles não são os coeficientes verdadeiros para toda a população. As estimativas dos parâmetros de regressão têm alguns erros associados a elas. Além de seus valores estimados, é útil fornecer um intervalo de confiança para os parâmetros. 

Use the lm() function to build a linear model based on the Orange dataset to predict the circumference (in mm) of orange trees given their age (in days):-

model_orange <- lm(circumference ~ age, data = Orange)

Verifique os coeficientes desse modelo linear:

model_orange

Esse comando mostra os parâmetros do modelo (interceptação e inclinação) conforme abaixo:

Coefficients: (Intercept)          age
                              17.3997       0.1068  

Use a função confint() para calcular os intervalos de confiança de 95%:

confint(model_orange, level = 0.95)

Agora você pode ver os intervalos de confiança de 95% da inclinação e da interceptação estimadas pelo modelo:

                          2.5 %                   97.5 %
(Intercept)     -0.14328303       34.9425835 
age                  0.08993141          0.1236092

Intervalo de confiança de uma previsão de resposta média 

Use o modelo de regressão criado acima para prever a circunferência média esperada de árvores com 900 dias de idade. Use o parâmetro interval para especificar um intervalo de confiança. 

predict(model_orange, data.frame(age = 900), interval = "confidence", level = 0.95)  

O resultado inclui a previsão (fit) e o intervalo de confiança (lwr e upr para os limites inferior e superior), conforme mostrado abaixo:

       fit                    lwr              upr
 1     113.4929        105.3211       121.6647

Implementação de intervalos de previsão no R

Use o mesmo modelo acima para prever a circunferência específica de uma laranjeira individual com 900 dias de idade. Use o parâmetro interval para especificar que você deseja o intervalo de previsão. 

> predict(model, data.frame(age = 900), interval = "prediction", level = 0.95)  

O resultado é semelhante ao exemplo abaixo:

       fit                    lwr              upr
1      113.4929        64.5118        162.4741

Observe que, em ambos os casos, o valor previsto da circunferência é o mesmo - 113,49. Entretanto, o intervalo de previsão é muito maior do que o intervalo de confiança. O intervalo de confiança da previsão é o intervalo que se espera que contenha a circunferência média das árvores com 900 dias de idade. O intervalo de previsão é o intervalo esperado da circunferência de uma árvore individual com 900 dias de idade. Isso ocorre porque pode haver uma variação consideravelmente maior em árvores individuais, que é suavizada quando se considera o valor médio. 

Equívocos e armadilhas comuns

Os intervalos estatísticos são comumente usados em campos estatísticos aplicados, como análise de dados, produtos farmacêuticos, econometria, etc. Para quem não tem formação acadêmica em estatística, é fácil confundir intervalos de confiança e intervalos de previsão. 

Alguns equívocos comuns são discutidos abaixo: 

• Fazer uma previsão sem considerar o intervalo de previsão. 
• Quando você usa um modelo de regressão para prever o valor da variável dependente para um determinado valor da variável independente, a equação de regressão fornece o valor esperado da variável dependente. O valor real raramente corresponde ao valor esperado, mas está dentro de um determinado intervalo do valor esperado, conforme especificado pelo intervalo de previsão. 
• Supondo que uma análise de regressão envolva apenas intervalos de previsão.
• Você faz dois tipos de previsões usando modelos de regressão: 1) prever um valor futuro e 2) prever a resposta média. No exemplo da laranjeira, você pode tentar prever 1) a circunferência de uma laranjeira específica com 900 dias de idade ou 2) a circunferência média de todas as árvores com 900 dias de idade. Em ambos os casos, o valor esperado é o mesmo. No entanto, o primeiro envolve o intervalo de previsão, e o segundo envolve o intervalo de confiança. 
• Acreditando que o intervalo mais estreito é o melhor.
• Às vezes, você pode se sentir tentado a usar apenas o intervalo mais estreito ao usar o resultado de um estudo de regressão. O intervalo de confiança não é, de alguma forma, "melhor" porque é mais estreito. Ele é mais estreito porque fornece o intervalo para algo diferente do que o intervalo de previsão faz. Considere se você está tentando prever o valor médio da variável dependente ou se deseja prever um ponto de dados individual.
• Confundir um intervalo de confiança com um intervalo de previsão. 
• Se a sua previsão envolver a determinação do valor de um parâmetro populacional a partir de uma amostra ou a previsão da resposta média (valor médio) a partir de uma regressão, você usará o intervalo de confiança. Se você tentar prever alguma propriedade de um ponto de dados individual com base em uma regressão, use o intervalo de previsão. 

Conclusão

Este artigo apresentou uma visão geral dos intervalos de confiança e intervalos de previsão. Ele também explica a diferença entre esses conceitos de aparência semelhante e oferece exemplos práticos de quando você deve usar cada tipo de intervalo. O artigo também mostrou como calcular a previsão e os intervalos de confiança usando a linguagem de programação R. 

Para saber como aplicar fórmulas estatísticas usando Python, consulte o curso DataCamp sobre estatísticas em Python. Por fim, se você estiver se preparando para entrevistas de emprego que envolvam estatística, confira o curso do DataCamp sobre perguntas de entrevista sobre estatística em Python.