Probabilidade condicional: Um olhar mais atento

Imagine que você está desenvolvendo um sistema de detecção de spam para e-mail. Inicialmente, você pode marcar um e-mail como suspeito se ele contiver determinadas palavras-chave. Mas e se você descobrir que esse e-mail veio de um remetente confiável? Ou se ela foi enviada em um horário incomum? Cada nova informação altera a probabilidade de o e-mail ser spam. Essa atualização dinâmica das probabilidades com base em novas evidências está no cerne da probabilidade condicional, um conceito que impulsiona muitos aplicativos modernos de ciência de dados, desde a filtragem de e-mails até a detecção de fraudes. 

Para aqueles que estão iniciando sua jornada com os conceitos de probabilidade, a Folha de dicas de introdução às regras de probabilidade oferece uma referência útil para os princípios e fórmulas fundamentais. O curso de Introdução à Estatística constrói uma base sólida ao explorar as distribuições de probabilidade e suas propriedades, que formam a base para você entender como a probabilidade condicional funciona na prática. Esses recursos oferecem um caminho estruturado para que você desenvolva fundamentos sólidos nos conceitos que exploraremos neste artigo.

O que é probabilidade condicional?

A probabilidade condicional mede a probabilidade de um evento ocorrer quando sabemos que outro evento já ocorreu. Quando recebemos novas informações sobre um evento, ajustamos nossos cálculos de probabilidade de acordo.

Para entender esse conceito, vamos explorar um exemplo com cartas de baralho. Quando você tira uma carta de um baralho padrão, há 52 resultados possíveis. Se você quiser tirar um rei, sua probabilidade inicial é de 4/52 (cerca de 7,7%), pois há quatro reis no baralho. Mas o que acontece se alguém lhe disser que a carta que você tirou é uma carta com cara? Essa nova informação muda tudo - a probabilidade de você ter um rei agora é muito maior, 4/12 (cerca de 33,3%), já que há apenas doze cartas com figuras no total.

Essa relação entre as probabilidades tem uma definição matemática precisa:

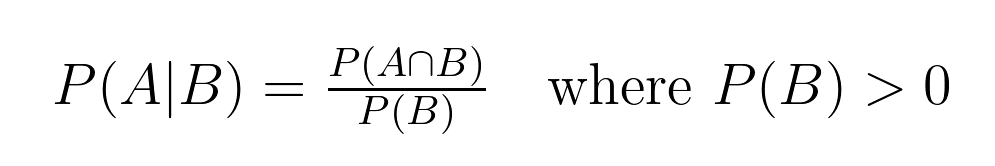
Essa fórmula nos ajuda a calcular a probabilidade condicional, em que:

• P(A|B) representa a probabilidade de ocorrência do evento A, considerando que o evento B tenha ocorrido. Isso é lido como "a probabilidade de A dado B".
• P(A∩B) representa a probabilidade conjunta, ou seja, a probabilidade de ambos os eventos A e B ocorrerem juntos. Isso é lido como "a probabilidade da interseção A com B".
• P(B) representa a probabilidade de ocorrência do evento B.

Em nosso exemplo de cartão:

• O evento A é "desenhar um rei"
• O evento B é "tirar uma carta de face"
• P(A|B) = 4/12 (probabilidade de você obter um rei, já que temos uma carta de face)
• P(A∩B) = 4/52 (probabilidade de você tirar um rei, que é sempre uma carta de face)
• P(B) = 12/52 (probabilidade de você tirar qualquer carta com a face)

Para entender melhor como a probabilidade condicional funciona na prática, podemos usar um diagrama de árvore. Os diagramas de árvore são particularmente úteis porque mostram como cada nova informação altera nossas probabilidades:

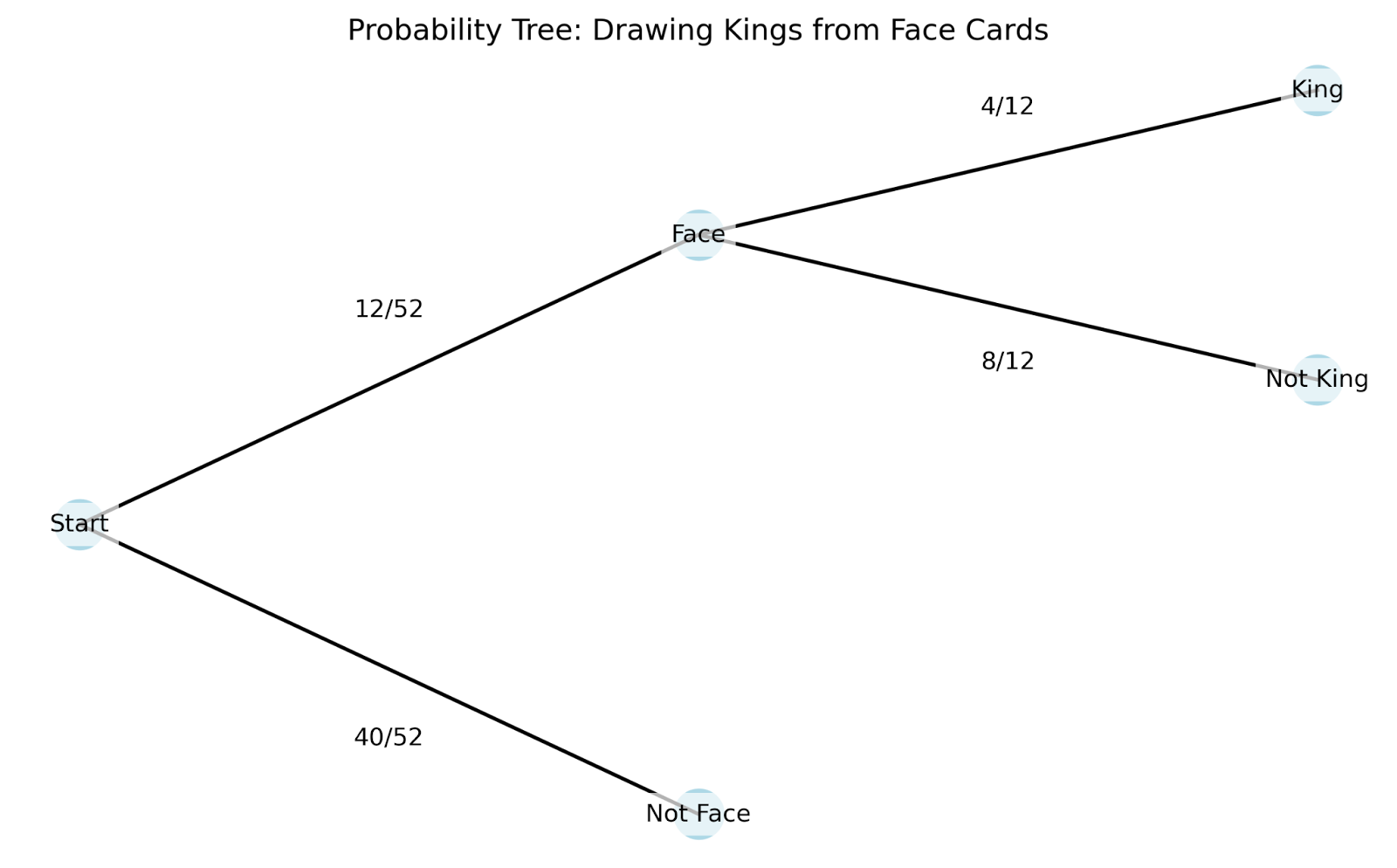
Vamos ver como esse diagrama de árvore funciona:

1. Começamos na raiz (ponto mais à esquerda) com todas as 52 cartas.
2. Os primeiros ramos mostram nossa primeira informação - é uma carta com face ou não?
3. Se você seguir o ramo da carta com a face, ele se dividirá novamente com base em nossa segunda informação - é um rei?

O diagrama de árvore nos ajuda a entender vários conceitos-chave da probabilidade condicional:

• Espaço de amostragem: Todos esses são resultados possíveis em nosso cenário. O espaço de amostra inicial é de 52 cartas, mas ele é "reduzido" para 12 cartas quando sabemos que temos uma carta de face.
• Eventos: Esses são resultados específicos nos quais estamos interessados, como "tirar uma carta de face" ou "tirar um rei". Os galhos de nossa árvore representam eventos diferentes.
• Probabilidade conjunta: Essa é a probabilidade de vários eventos ocorrerem juntos. Em nossa árvore, podemos descobrir isso multiplicando as probabilidades ao longo de um caminho. Por exemplo, a probabilidade de você tirar um rei E de ele ser uma carta de face é (12/52) × (4/12) = 4/52.
• Probabilidade marginal (incondicional): Essa é a probabilidade de ocorrência de um evento sem considerar nenhuma outra informação. Em nosso exemplo, isso é como a probabilidade inicial de 4/52 de tirar um rei antes de sabermos qualquer outra coisa sobre a carta.

A beleza da probabilidade condicional é que ela nos permite atualizar nossas probabilidades à medida que obtemos novas informações. Da mesma forma que ajustamos nossa probabilidade de ter um rei de 7,7% para 33,3% quando soubemos que tínhamos uma carta de face, a probabilidade condicional nos dá uma maneira formal de recalcular as probabilidades com base em novas evidências.

A fórmula da probabilidade condicional

A estrutura matemática da probabilidade condicional nos fornece ferramentas para analisar cenários complexos que envolvem vários eventos. Vamos explorar as principais propriedades.

Principais propriedades da probabilidade condicional

Essas propriedades matemáticas nos ajudam a resolver problemas complexos com mais eficiência:

1. Propriedade Independence

Quando dois eventos A e B são independentes, sabemos que a ocorrência de um não afeta a probabilidade do outro. Matematicamente, isso é: P(A|B) = P(A), que é lido como: "a probabilidade de A dado B é igual à probabilidade de A".

Por exemplo, se lançarmos um dado e jogarmos uma moeda, o fato de você tirar cara na moeda não altera a probabilidade de tirar um seis. A fórmula nos mostra: P(Six|Heads) = P(Six) = 1/6

2. Regra de complemento

Para qualquer evento A dada a condição B, as probabilidades de A e seu complemento A' (leia-se "A prime") devem somar 1. Matematicamente, isso é: P(A|B) + P(A'|B) = 1, que é lido como: "A probabilidade de A dado B mais a probabilidade de um complemento de A dado B é igual a 1."

Em nosso exemplo anterior de cartão: P(Rei|Cartão de face) + P(Não Rei|Cartão de face) = 4/12 + 8/12 = 1

A regra da multiplicação e a regra da cadeia

A regra de multiplicação vincula as probabilidades conjuntas às probabilidades condicionais: P(A ∩ B) = P(A|B) × P(B). Dizemos: "A probabilidade de A interseção B é igual à probabilidade de A dada B vezes a probabilidade de B".

Isso se estende a vários eventos por meio da regra da cadeia. Para três eventos A, B e C: P(A ∩ B ∩ C) = P(A|B ∩ C) × P(B|C) × P(C). Ou seja, "A probabilidade de A interseção B interseção C é igual à probabilidade de A dada B interseção C vezes a probabilidade de B dada C vezes a probabilidade de C".

Vamos ver isso em ação com uma sequência de sorteio de cartas:

1. Tirar um rei (K)
2. Das cartas restantes, você tira uma rainha (Q)
3. Das cartas restantes, você tira um ás (A)

P(K ∩ Q ∩ A) = P(A|K ∩ Q) × P(Q|K) × P(K) = (4/50) × (4/51) × (4/52)

A regra da cadeia torna-se particularmente valiosa no aprendizado de máquina, especialmente em redes bayesianas, onde precisamos modelar dependências complexas entre várias variáveis. Ao analisar dados, frequentemente nos deparamos com situações em que os eventos seguem uma sequência natural, e a regra da cadeia nos ajuda a decompor esses cenários complexos em cálculos mais simples e gerenciáveis.

Exemplos para ilustrar a probabilidade condicional

Vamos analisar dois dos exemplos mais comuns e pensar também em como a probabilidade condicional pode aparecer em seu trabalho.

Exemplos clássicos

Esses dois exemplos são muito comuns e vale a pena estudá-los, especialmente se você estiver fazendo uma entrevista:

Rolagem de dados: Compreensão de espaços amostrais reduzidos

Quando lançamos um dado, nosso espaço amostral começa com seis possibilidades: {1, 2, 3, 4, 5, 6}. O conhecimento de informações parciais sobre o lançamento altera nossos cálculos de probabilidade de uma maneira específica. Vamos ver como:

Probabilidade inicial de rolar um 6: P(6) = 1/6

Se soubermos que a rolagem foi par, nosso espaço amostral se reduzirá a {2, 4, 6}: P(6 | par) = 1/3

Bolinhas de gude: Dependências sequenciais

Uma sacola contém 5 bolinhas de gude azuis e 3 bolinhas de gude vermelhas. Quando sorteamos bolinhas de gude sem reposição, cada sorteio afeta as probabilidades dos sorteios subsequentes.

Primeiro sorteio - probabilidade de azul: P(blue₁) = 5/8

Segundo sorteio, já que o primeiro foi azul: P(azul₂ | azul₁) = 4/7

Esse exemplo complementa nosso exemplo anterior de cartão, destacando as dependências sequenciais.

Exemplos do mundo real

Exames médicos: Avaliação da precisão do teste

Os exames médicos oferecem uma aplicação perfeita da probabilidade condicional na avaliação da precisão do teste. Para qualquer teste de diagnóstico, precisamos entender quatro probabilidades condicionais principais:

1. P(T+ | D+): Probabilidade de um teste positivo se o paciente tiver a doença (sensibilidade) 
2. P(T- | D-): Probabilidade de um teste negativo se o paciente não tiver a doença (especificidade) 
3. P(T+ | D-): Probabilidade de um teste positivo se o paciente não tiver a doença (taxa de falsos positivos) 
4. P(T- | D+): Probabilidade de um teste negativo se o paciente tiver a doença (taxa de falso negativo)

Ao avaliar o desempenho desse teste, os profissionais médicos usam essas probabilidades condicionais para:

1. Comparar a precisão do teste em diferentes populações de pacientes
2. Determinar quando vários testes podem ser necessários
3. Definir limites apropriados para resultados positivos/negativos

Por exemplo, se testarmos 1.000 pacientes e obtivermos 100 resultados positivos, poderemos usar essas probabilidades condicionais para estimar quantos são verdadeiros positivos e quantos são falsos positivos. Essa análise ajuda os profissionais da área médica a equilibrar os riscos de perder um diagnóstico com os custos e a ansiedade dos alarmes falsos.

Avaliação de risco financeiro

As empresas de investimento usam a probabilidade condicional para avaliar os riscos de mercado. Considere um gerente de portfólio que acompanha a volatilidade do mercado:

A volatilidade diária do mercado pode ser Baixa (L), Média (M) ou Alta (H).

Os dados históricos mostram: 

• P(H amanhã | H hoje) = 0,70 
• P(M amanhã | H hoje) = 0,25 
• P(L amanhã | H hoje) = 0,05

Essas informações ajudam os gerentes:

• Ajustar as alocações do portfólio com base nas condições atuais do mercado
• Definir limites de risco para sistemas de negociação automatizados
• Desenvolver planos de contingência para períodos de alta volatilidade sustentada

Probabilidade condicional e teorema de Bayes

Nossa exploração dos testes médicos destacou uma distinção importante: A probabilidade de ter uma doença com um teste positivo é diferente da probabilidade de ter um teste positivo com a doença. O Teorema de Bayes fornece uma estrutura formal para navegar nessa relação, permitindo-nos atualizar nossas estimativas de probabilidade à medida que surgem novas evidências.

Entendendo o teorema de Bayes

O Teorema de Bayes expressa a relação entre duas probabilidades condicionais: P(A|B) = [P(B|A) × P(A)] / P(B). Você pode ler essa equação da seguinte forma: "A probabilidade de A dado B é igual à probabilidade de B dado A vezes a probabilidade de A, dividida pela probabilidade de B."

Cada componente desempenha uma função:

• P(A): A probabilidade prévia - nossa crença inicial sobre A antes de ver a evidência B
• P(B|A): A probabilidade - quão provável é a evidência B se A for verdadeira
• P(B): A probabilidade total de observar a evidência B
• P(A|B): A probabilidade posterior - nossa crença atualizada sobre A depois de ver a evidência B

Vamos ver como isso funciona na prática com nosso cenário de testes médicos, agora expandido para mostrar a análise bayesiana completa.

Um exemplo de teste médico

Considere uma condição médica que afeta 2% da população. Um novo teste de diagnóstico:

• 95% de sensibilidade: P(teste positivo | tem condição) = 0,95
• 90% de especificidade: P(teste negativo | sem condição) = 0,90

Quando o teste de um paciente é positivo, como devemos atualizar nossa crença sobre sua condição?

Vamos resolver isso passo a passo:

1. Probabilidade prévia (antes do teste): P(condição) = 0,02 (taxa populacional de 2%)
2. Probabilidade de um teste positivo dada a condição: P(positivo|condição) = 0,95 (sensibilidade do teste)
3. Probabilidade total de um teste positivo: P(positivo) = P(positivo|condição) × P(condição) + P(positivo|sem condição) × P(sem condição) = 0,95 × 0,02 + 0,10 × 0,98 = 0,019 + 0,098 = 0,117
4. Probabilidade posterior (usando o Teorema de Bayes): P(condição|positivo) = [0,95 × 0,02] / 0,117 ≈ 0,162 ou 16,2%

Essa análise revela que, mesmo com um teste positivo, a probabilidade de você ter a doença é de apenas 16,2% - muito maior do que os 2% iniciais, mas talvez menor do que a intuição possa sugerir.

O poder da atualização bayesiana

O Teorema de Bayes se destaca quando recebemos várias evidências. A probabilidade posterior de cada cálculo torna-se a probabilidade anterior para a próxima atualização. Por exemplo, se nosso paciente tiver um segundo teste positivo:

1. Novo antes: P(condição) = 0,162 (do nosso primeiro cálculo)
2. Likelihood: P(positivo|condição) = 0,95
3. Calcule o novo valor posterior...

Essa atualização sequencial fornece uma estrutura matemática para incorporar novas evidências em nossas estimativas de probabilidade. A beleza da inferência bayesiana está em sua capacidade de quantificar como nossas crenças devem mudar à medida que coletamos novas informações, fornecendo um método formal para atualizar as probabilidades à luz das evidências.

Aplicativos em ciência de dados

Vamos ver como a probabilidade condicional aparece na ciência de dados. 

Modelagem preditiva

O classificador Naive Bayes, uma das ferramentas mais simples e poderosas do aprendizado de máquina, aplica o Teorema de Bayes para prever categorias com base nas probabilidades de recursos. Ao classificar um e-mail como spam ou não spam, por exemplo, o algoritmo calcula a probabilidade condicional de um e-mail ser spam com base nas palavras que ele contém. Embora você faça a suposição "ingênua" de que os recursos são independentes, essa simplificação costuma funcionar surpreendentemente bem na prática.

As árvores de decisão adotam uma abordagem diferente para a probabilidade condicional, dividindo os dados com base nos valores dos recursos para criar subconjuntos condicionais. Em cada nó, a árvore faz perguntas como: "Qual é a probabilidade de nossa variável-alvo com esse valor específico de recurso?" Essas divisões continuam até atingirmos subconjuntos puros ou quase puros, essencialmente criando um mapa de probabilidades condicionais que orientam nossas previsões.

Gerenciamento de riscos

Os sistemas de pontuação de crédito usam probabilidades condicionais para avaliar a probabilidade de inadimplência do empréstimo com base em várias características do cliente. Por exemplo, um banco pode calcular a probabilidade de inadimplência com base no nível de renda, no histórico de crédito e na situação empregatícia. Esses cálculos se tornam mais sofisticados quando se consideram vários riscos dependentes, por exemplo, como a probabilidade de inadimplência hipotecária pode mudar em função de uma recessão e do aumento das taxas de juros. Os modelos de risco de investimento usam probabilidades condicionais para estimar o valor em risco (VaR), calculando a probabilidade de níveis específicos de perda, dadas as condições atuais do mercado. Os gerentes de portfólio usam essas probabilidades condicionais para ajustar as alocações de ativos, entendendo como o risco de um investimento pode mudar em função do desempenho de outros no portfólio.

Aprendizado de máquina

As redes bayesianas representam a aplicação mais direta da probabilidade condicional no aprendizado de máquina, modelando as relações entre as variáveis como um gráfico direcionado em que o estado de cada nó depende de seus pais. Essas redes são excelentes em tarefas como diagnóstico médico, em que a probabilidade de várias condições depende de vários sintomas interconectados e resultados de testes.

Os modelos gráficos probabilísticos usam dependências condicionais para representar relações complexas nos dados, o que os torna valiosos para tarefas como reconhecimento de imagens e processamento de linguagem natural. Mesmo os modelos de aprendizagem profunda, embora não sejam explicitamente probabilísticos, geram probabilidades condicionais em suas camadas finais ao fazer classificações. A função softmax, comumente usada em redes neurais, transforma as pontuações brutas em probabilidades condicionais, informando a probabilidade de cada classe possível com base nos dados de entrada.

Armadilhas comuns e interpretações errôneas

Ao trabalhar com probabilidade condicional, três equívocos principais geralmente levam a conclusões incorretas.

• A falácia do inverso, também conhecida como confusão do inverso, ocorre quando misturamos P(A|B) com P(B|A). Vimos isso em nosso exemplo de testes médicos - a probabilidade de ter uma condição se o teste for positivo é diferente da probabilidade de o teste ser positivo se você tiver a condição.
• A negligência da taxa básica ocorre quando nos concentramos nas probabilidades condicionais e ignoramos a probabilidade subjacente de um evento. Por exemplo, se uma doença rara afetar apenas 1 em cada 10.000 pessoas, até mesmo um teste altamente preciso poderá gerar a maioria dos falsos positivos simplesmente porque a doença é muito incomum.
• A terceira armadilha envolve a ponderação incorreta das evidências ao atualizar as probabilidades. As pessoas tendem a dar mais peso a evidências recentes ou dramáticas e menos peso a informações estáveis sobre o histórico. No comércio financeiro, por exemplo, os investidores podem reagir de forma exagerada às notícias recentes do mercado e ignorar as probabilidades de longo prazo do mercado.

Tópicos avançados e considerações adicionais

Por fim, vamos analisar algumas ideias mais complicadas que se baseiam no que temos praticado.

Condicionamento em eventos de probabilidade zero

Quando passamos de distribuições de probabilidade discretas para contínuas, nos deparamos com um desafio interessante: pontos específicos em uma distribuição contínua têm probabilidade zero. Considere a medição da altura exata de uma pessoa - embora possamos dizer que a probabilidade de alguém ter entre 170 e 171 centímetros é significativa, a probabilidade de alguém ter exatamente 170,5432... centímetros é tecnicamente zero. No entanto, muitas vezes queremos nos condicionar a essas medidas precisas. A probabilidade condicional regular fornece uma estrutura matemática para lidar com essas situações, estendendo nossos conceitos básicos a casos contínuos por meio do uso de funções de densidade e teoria de medidas. Essa extensão nos permite entender afirmações como "a distribuição de probabilidade do peso de uma pessoa, considerando que ela tem exatamente 170,5 centímetros de altura".

Probabilidade condicional parcial e extensões

A condicionalização de Jeffrey expande a probabilidade condicional tradicional para situações em que nossa nova evidência não é certa, mas tem sua própria probabilidade. Diferentemente do condicionamento padrão, em que assumimos certeza absoluta sobre nossas novas informações, a regra de Jeffrey nos permite atualizar nossas crenças com base em evidências incertas. Isso corresponde melhor aos cenários do mundo real, em que as novas informações geralmente vêm com algum grau de incerteza. Por exemplo, em vez de saber com certeza que um exame médico é positivo, podemos saber que a probabilidade de ser positivo é de 80%. A regra de Jeffrey oferece um método formal para atualizar as probabilidades nessas situações mais complexas.

Conclusão

A probabilidade condicional fornece uma estrutura matemática para atualizar nossas crenças à medida que surgem novas informações. Ao longo deste artigo, vimos como esse conceito se aplica a vários campos, desde o diagnóstico médico até a avaliação de riscos financeiros. Os princípios que exploramos nos ajudam a entender como a probabilidade muda com novas evidências, permitindo decisões mais informadas em aplicativos de ciência de dados. Esse entendimento torna-se particularmente valioso quando se trabalha com algoritmos de classificação, modelos de risco e sistemas de aprendizado de máquina em que as atualizações de probabilidade ocorrem continuamente.

À medida que você continua a desenvolver sua experiência em probabilidade e inferência estatística, vários cursos podem aumentar sua compreensão desses conceitos por meio de uma lente bayesiana. Nosso curso Fundamentals of Bayesian Data Analysis in R apresenta os princípios fundamentais e suas aplicações práticas, enquanto nosso curso Bayesian Modeling with RJAGS mostra como implementar esses conceitos usando ferramentas estatísticas poderosas. Para usuários de Python, nosso curso Bayesian Data Analysis in Python oferece experiência prática na aplicação desses métodos a problemas do mundo real. Cada curso oferece um caminho para você expandir seu conhecimento sobre probabilidade e suas aplicações na ciência de dados moderna.