Distribuição de Poisson: Um guia abrangente

Em estatística e ciência de dados, a distribuição de Poisson é uma ferramenta importante para modelar eventos discretos que ocorrem em um intervalo fixo. Nomeada em homenagem ao matemático francês Siméon Denis Poisson, essa distribuição de probabilidade ajuda a analisar e prever eventos raros, o que a torna valiosa para profissionais de dados em vários campos.

Se você é novo em estatística, nosso curso de Introdução à Estatística oferece uma base sólida para a compreensão desses conceitos. Para aqueles que estão prontos para realmente aprender a teoria da probabilidade, o curso Foundations of Probability in Python oferece uma exploração abrangente de conceitos probabilísticos, incluindo a distribuição de Poisson. 

O que é uma distribuição de Poisson?

A distribuição de Poisson é uma distribuição de probabilidade discreta que expressa a probabilidade de ocorrência de um determinado número de eventos em um intervalo fixo de tempo ou espaço. Ele pressupõe que esses eventos ocorram com uma taxa média conhecida e independentemente do tempo decorrido desde o último evento. Para entender a distribuição de Poisson, primeiro é útil saber a diferença entre distribuições discretas e contínuas.

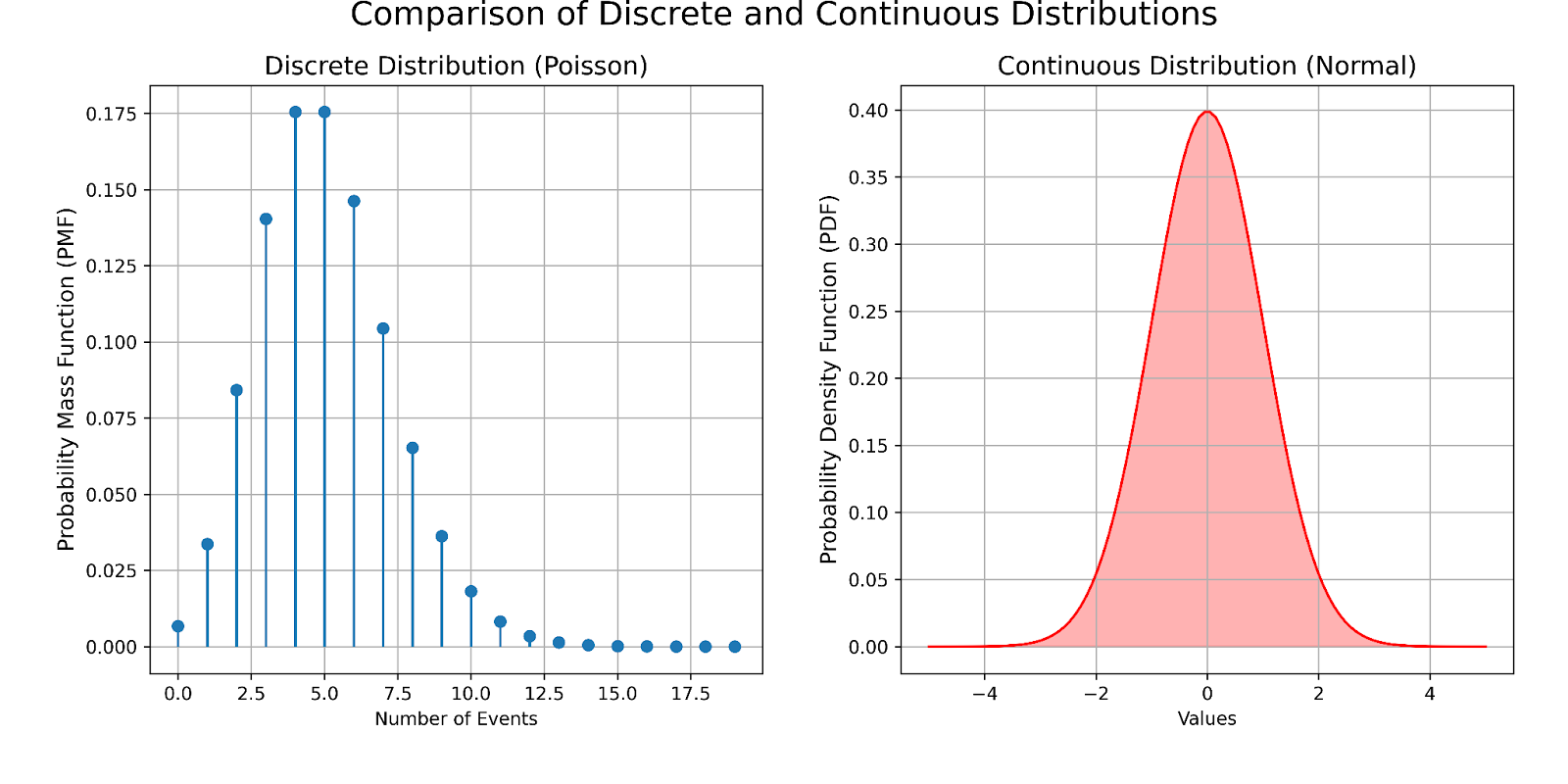
Distribuição de Poisson vs. uma distribuição contínua. Imagem do autor

Distribuições discretas

• Natureza: As distribuições discretas descrevem fenômenos em que os resultados podem ser contados em números inteiros. Eles são caracterizados por funções de massa de probabilidade (PMF) que atribuem uma probabilidade a cada resultado discreto possível.
• Visualização: No painel esquerdo, é mostrada a distribuição de Poisson, em que cada ponto representa a probabilidade de ocorrência de um número específico de eventos em um intervalo fixo. Essa distribuição é ideal para modelar dados de contagem, como o número de e-mails recebidos por hora. Você pode notar, também, que não há valores negativos no painel de distribuição de Poisson. Isso ocorre porque as distribuições de Poisson, por definição, não podem ter valores negativos.

Alguns exemplos de distribuições de probabilidade discretas incluem as distribuições Bernoulli e binomial. 

Distribuições contínuas

• Natureza: As distribuições contínuas são usadas para dados que podem assumir qualquer valor em um intervalo, inclusive decimais. Eles usam funções de densidade de probabilidade (PDF) para descrever as probabilidades de resultados em um determinado intervalo.
• Visualização: O painel direito ilustra a distribuição normal. A curva suave indica a densidade de valores em torno da média, e a área sob a curva entre quaisquer dois pontos fornece a probabilidade de você se enquadrar nesse intervalo. Esse tipo de distribuição é útil para medir quantidades como temperatura ou peso.

A distribuição normal, ou gaussiana, é um excelente exemplo de distribuição contínua.

Propriedades das distribuições de Poisson

Vamos dar uma olhada em algumas das características importantes da distribuição de Poisson.

Eventos em um intervalo fixo

Uma característica fundamental da distribuição de Poisson é sua capacidade de modelar eventos em um intervalo fixo. Esse intervalo pode ser de tempo (por exemplo, o número de clientes que chegam por hora) ou de espaço (por exemplo, o número de defeitos por metro quadrado de tecido). O modelo pressupõe que:

1. Os eventos ocorrem de forma independente.
2. A taxa média de ocorrência (λ) permanece constante durante o intervalo.
3. Dois eventos não podem ocorrer exatamente no mesmo instante.

Média e variância

Uma das propriedades mais marcantes da distribuição de Poisson é que sua média (valor esperado) é igual à sua variação. Ambos são representados pelo parâmetro λ (lambda), que denota o número médio de eventos no intervalo. Essa propriedade é exclusiva e ajuda a identificar se um conjunto de dados segue uma distribuição de Poisson. Matematicamente, isso pode ser representado na seguinte equação: 

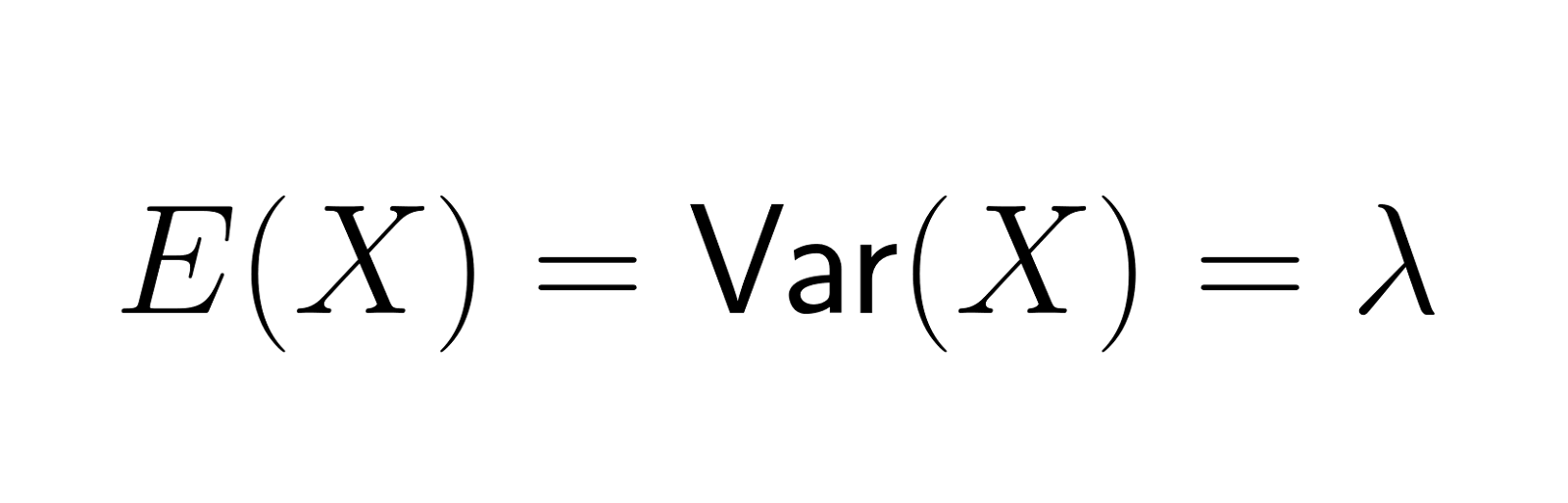
Essa igualdade implica que, à medida que o número esperado de eventos aumenta, o mesmo ocorre com a variabilidade no número real de ocorrências.

Skewness e forma

A forma da distribuição de Poisson varia de acordo com o valor de λ. Essa ilustração visual demonstra como λ afeta a assimetria da distribuição: 

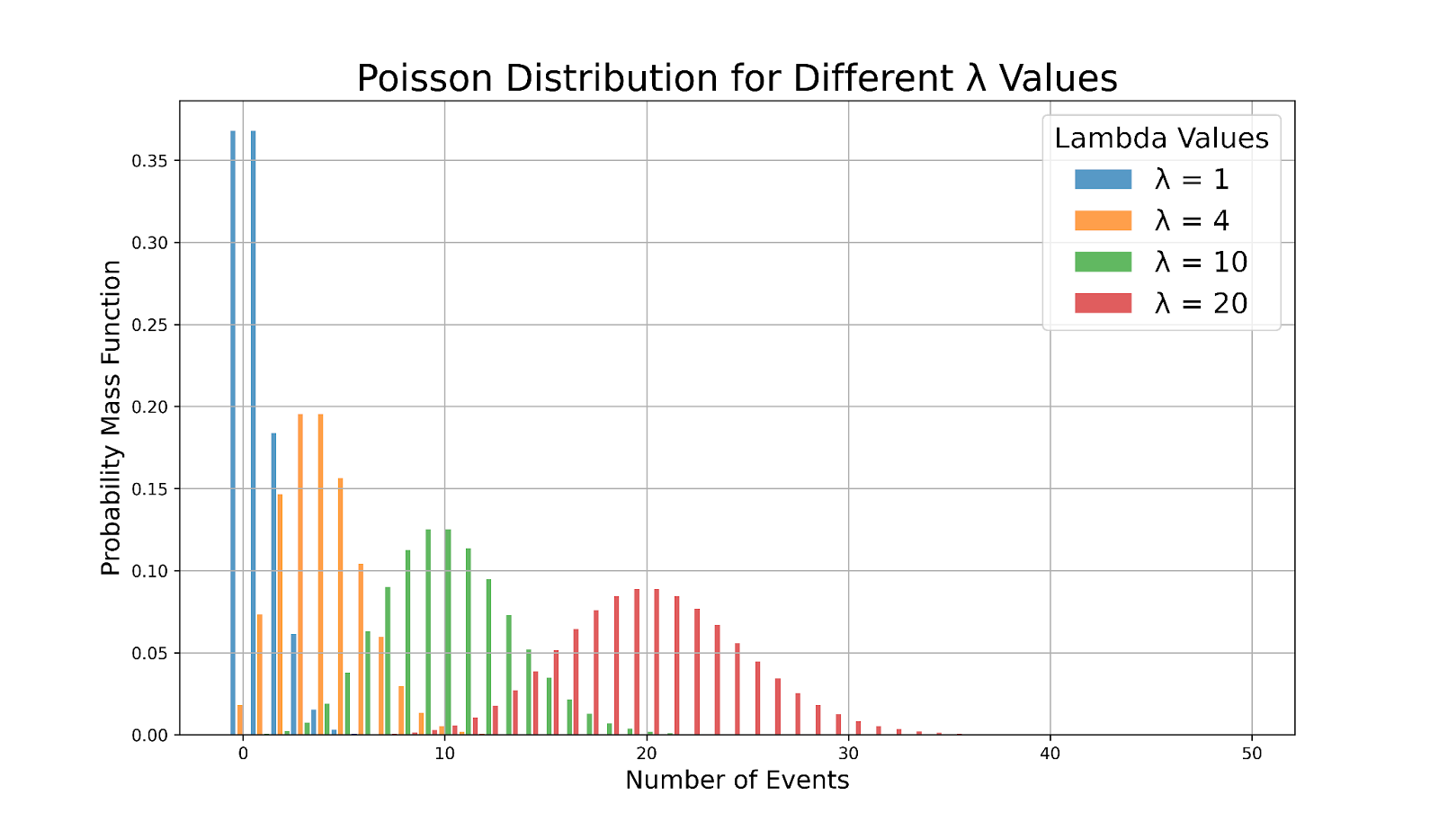
Distribuições de Poisson com diferentes valores lambda. Imagem do autor

• Para valores pequenos de λ (λ < 10), a distribuição é visivelmente inclinada para a direita. Isso significa que há mais ocorrências com menos eventos e menos ocorrências com um número maior de eventos.
• À medida que λ aumenta (λ > 10), a distribuição se torna mais simétrica e começa a se assemelhar a uma distribuição normal. Essa simetria indica que os dados estão mais uniformemente distribuídos em torno da média.

Essa mudança de formato afeta a forma como interpretamos as probabilidades e fazemos inferências a partir de dados com distribuição de Poisson. Por exemplo, uma distribuição simétrica simplifica muitos tipos de análises, como testes de hipóteses e estimativas de intervalos de confiança, porque a distribuição dos dados é mais previsível e equilibrada.

Fórmula de distribuição de Poisson

Dê uma olhada na fórmula da distribuição de Poisson. 

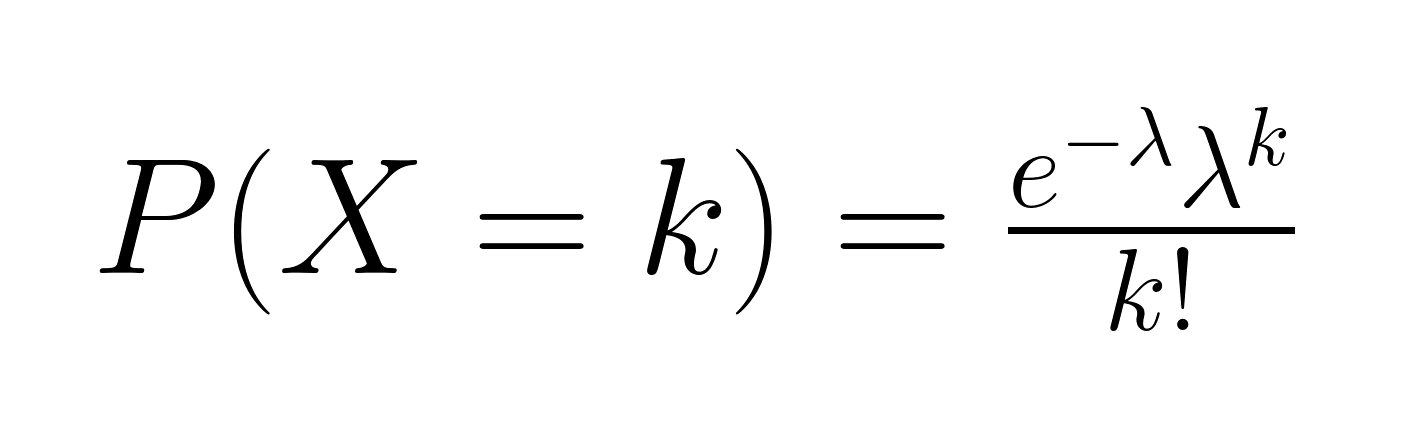
• O lado esquerdo (LHS) da fórmula da distribuição de Poisson, P(X = k), representa a probabilidade de ocorrência de exatamente k eventos em um intervalo fixo. Aqui, X é o número de eventos e k é o número específico no qual estamos interessados. Em outras palavras, o LHS nos diz qual é a probabilidade que estamos calculando.

• O numerador do lado direito (RHS),^e-λλk, tem duas partes. ^λk mostra a probabilidade de ocorrência de k eventos com base na taxa média λ. O ^e-λ é responsável pela aleatoriedade dos eventos, garantindo que a probabilidade diminua à medida que o número de eventos se desvia da taxa esperada.

• O denominador do lado direito (RHS), k! ajusta a quantidade de maneiras pelas quais os eventosx podem ocorrer. A notação fatorial calcula o número de arranjos possíveis, garantindo que a probabilidade reflita o fato de que a ordem dos eventos não importa.

Se você realmente quiser se tornar confiante no uso de Python para aprendizado de máquina, inicie nossa carreira de Cientista de Aprendizado de Máquina com Python, que permite que você pratique técnicas avançadas com conjuntos de dados reais.