Eigenvectors and Eigenvalues: Key Insights for Data Science

Eigenvectors and eigenvalues are fundamental concepts in linear algebra that have far-reaching implications in data science and machine learning. These mathematical entities provide valuable insights into the behavior of linear transformations, enabling us to understand the underlying structure of data, simplify complex datasets with a big number of features, and, therefore, enabling their processing to achieve the desired goal.

If this sounds like dimensionality reduction to you, you are right. Eigenvectors and eigenvalues work under the hood of many dimensionality reduction techniques, like principal component analysis (PCA). They are also the gears for spectral clustering, which involves dimensionality reduction as an initial step.

To have a grasp on the concept of the eigen world, you would need to have a fair understanding of prior concepts in linear algebra, mainly vectors and scalars, linear transformation, and determinants. If you are new to these concepts, you can take our hands-on Linear Algebra for Data Science in R course, or if you are a Python user, you can go through this SciPy tutorial on vectors and arrays.

What are Eigenvectors and Eigenvalues?

Let’s start from the fact that the “eigen” part of eigenvectors and eigenvalues actually has a meaning and is not the name of some guy who invented them. Eigen is a German word that can be roughly translated in this context as the “characteristic thing” or the “intrinsic thing” of something.

Now, imagine we subject a group of vectors to a linear transformation, like scaling, shearing, or rotation. Some vectors change their direction, and some vectors do not. The vectors that do not change their direction (or rotate to the exactly opposite direction) are what we call the eigenvectors, as they become the “characteristic” vectors of the transformation that happened (or the matrix they describe). The amount (magnitude) they happened to be scaled is the eigenvalue. That is, the eigenvalue is the scaling factor of the transformation.

Understanding Eigenvectors and Eigenvalues

To better understand the concepts of the two, let’s work through a geometric case and then move on to their application in data science.

Geometric interpretation

Imagine a two-dimensional space, in which we have three vectors, a blue one that rests on the x-axis, a red one that rests on the y-axis, and a green one that rests diagonally between the two. Now, we apply a scaling transformation along the y-axis with a factor of two, as shown in the images below.

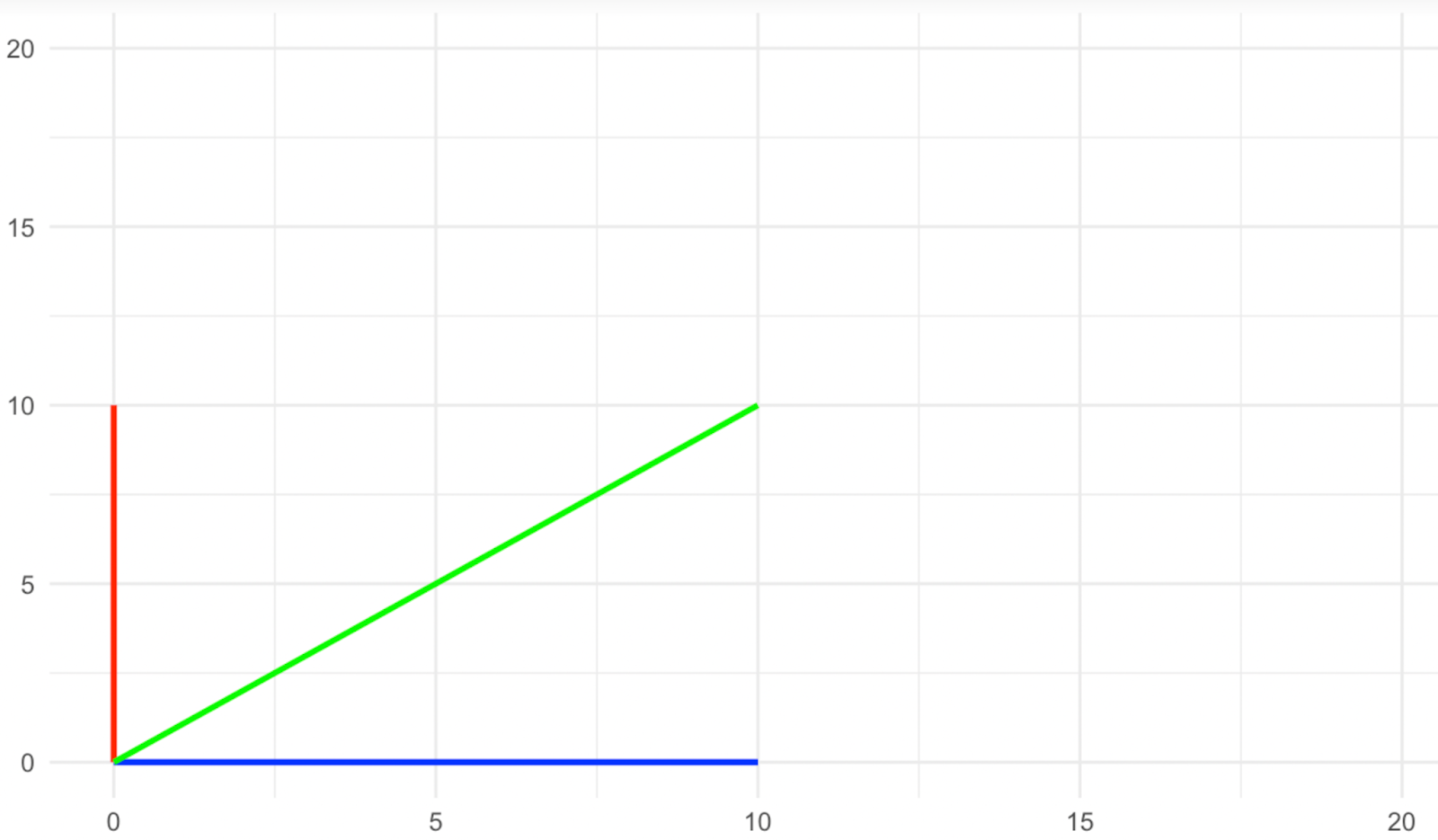
Vectors before stretching. Image by Author

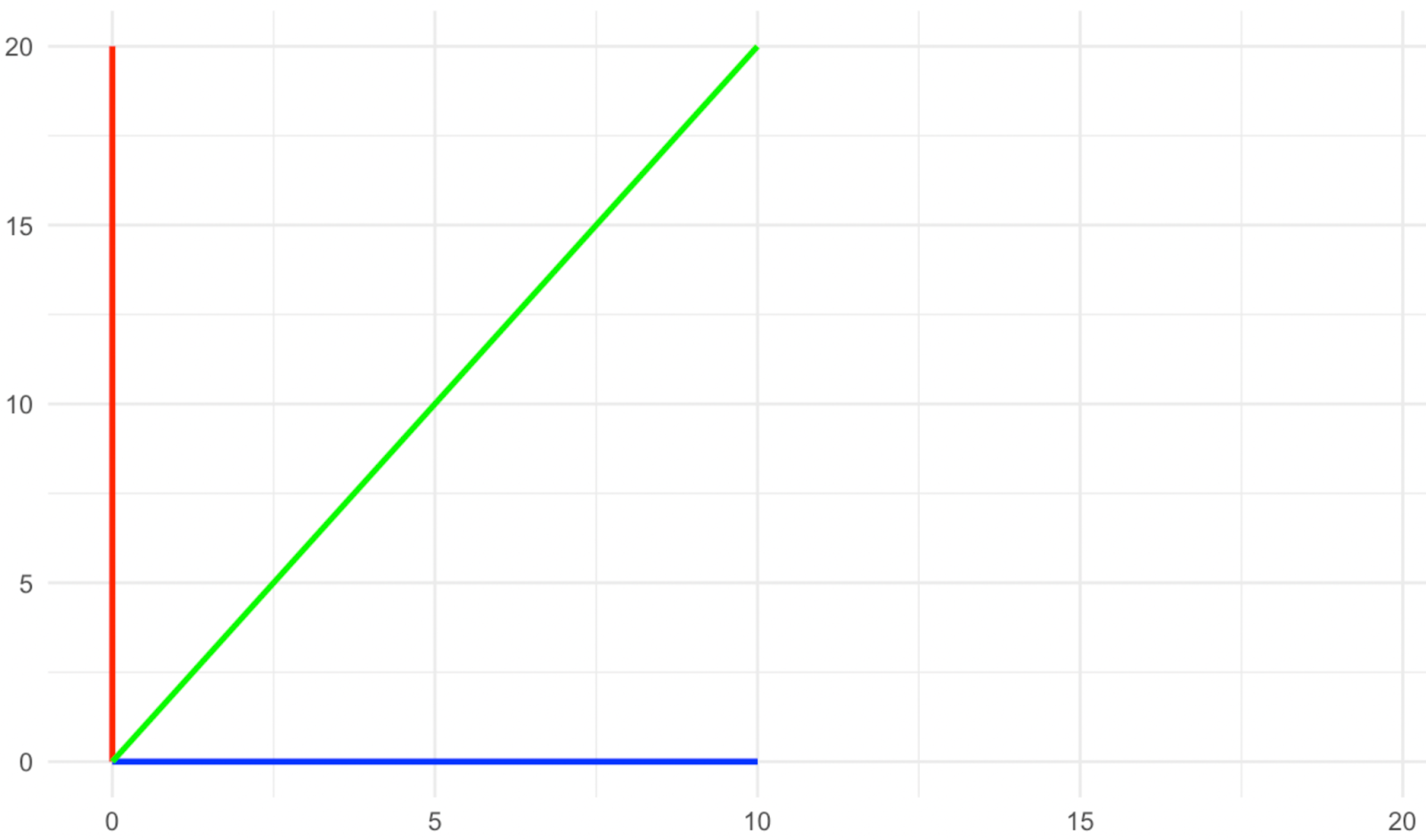
Vectors after stretching. Image by Author

What happened to the direction vectors? The red and blue ones did not change their direction with the scaling, while the green one did change its direction, right? Therefore, in this kind of transformation, the red and blue vectors are what we call the eigenvectors, as they become the characteristic vectors of the transformation.

Have a look again at the images above and see what happened to the magnitude of the eigenvectors (the red and blue ones). The blue eigenvector did not change its magnitude, while the red one doubled or, in a fancy way of saying, was scaled to the factor of two. The amount by which each of the eigenvectors was scaled with the transformation is what we call the eigenvalues. Therefore, the eigenvalue of the blue eigenvector here is 1 (think of this as a multiplication), while the eigenvalue of the red eigenvector is 2, as its magnitude was doubled.

Properties of eigenvalues

Consider the transformation shown in the images below, and first of all, think of what the eigenvectors are in this case. If you said it’s the three vectors, the red, green, and yellow, you are right, since they all point in the exact opposite direction after the transformation. We see that the sign of the number (the eigenvalue) can tell us additional information about the transformation that took place. A positive eigenvalue indicates that the transformation did not include a rotation, while a negative eigenvalue indicates that the transformation included a rotation of the eigenvector around its origin.

Vectors before rotation. Image by Author

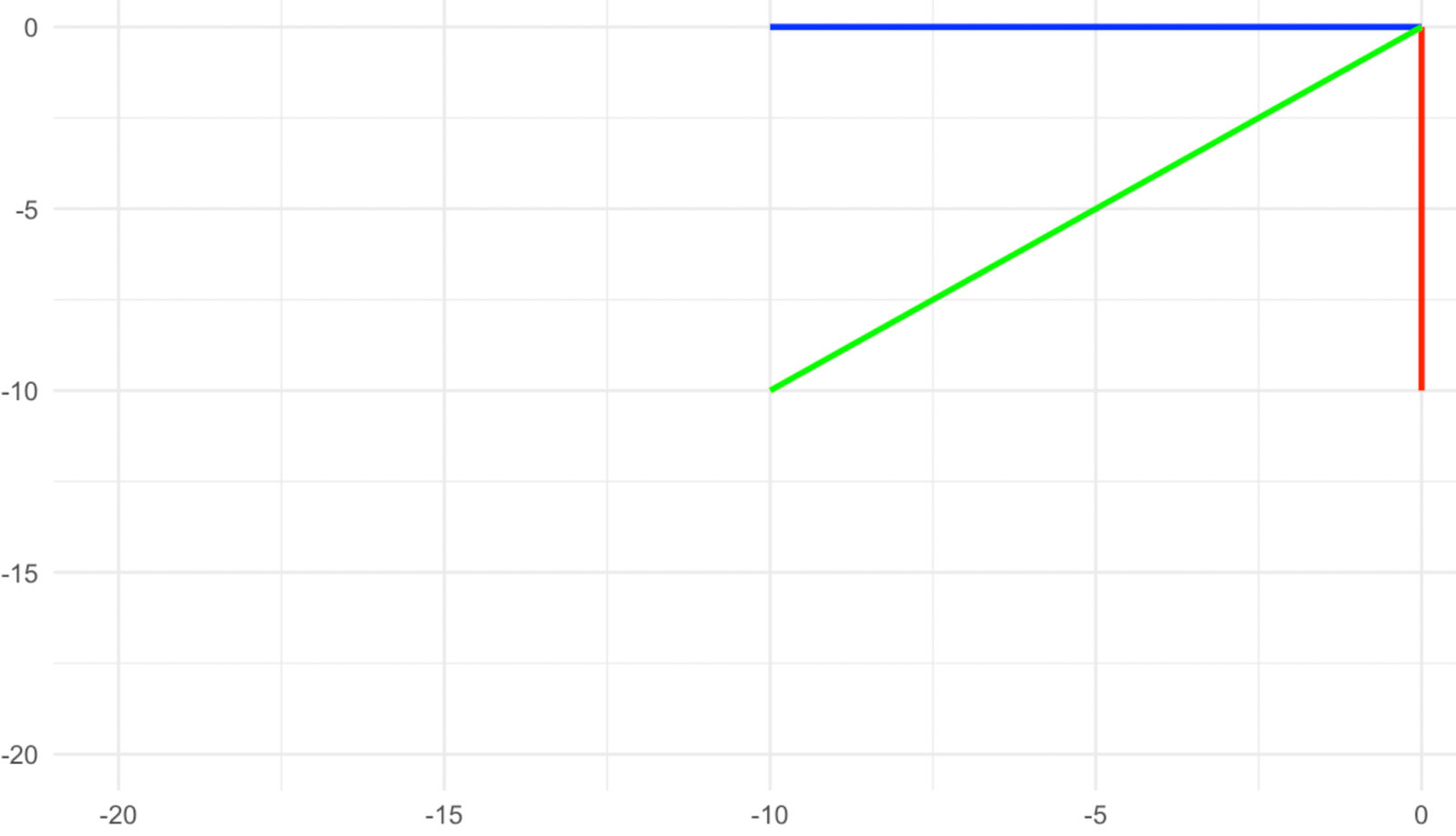
Vectors after rotation. Image by Author

Now, what is the eigenvalue of each of these eigenvectors? The fact that their magnitude remains the same means that the eigenvalue is 1, but the fact that they also rotated means that the sign of the 1 must be negative. Therefore, the eigenvalue in this case is -1.

In our example, the eigenvalues are simple (they are all 1), but eigenvalues can be any number, whether it is an integer or a whole number, like 1 and 2, or a rational (fraction) like ½ and 0.75. They can be what is called irrational numbers like the value of π. Eigenvalues can even be complex numbers, such as a + bi, where “a” and “b” are separately real numbers and “i” is an imaginary unit, like the square root of -1. The complex eigenvalues can also indicate the type of linear transformation that took place, whether it is also a rotation or a more complex one like oscillation.

How to Calculate Eigenvectors and Eigenvalues

While libraries in the base package in R, and libraries in Python like SciPy and NumPy, can easily find eigenvectors and eigenvalues, understanding the equations behind them is extremely valuable. In this section, we will review what is called the characteristic equation, which calculates the eigenvectors and eigenvalues given a simple matrix step by step. Then, we will mention other mathematical computation methods for larger matrices (i.e. large datasets).

Characteristic equation

We can find the eigenvectors and eigenvalues using what is known as the characteristic equation. Using the characteristic equation, the eigenvalues are found first before the eigenvectors. Once the eigenvalue is known, it is then used to calculate the corresponding eigenvector by solving a system of linear equations. 

Step 1: Start with the matrix transformation equation

For a matrix 𝐴 and a vector 𝑣, the basic equation for eigenvectors and eigenvalues is:

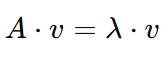
This means that when matrix 𝐴 acts on vector 𝑣, the result is a scaled version of 𝑣. Here:

• 𝐴 is a matrix (a square grid of numbers).
• 𝑣 is the eigenvector
• λ (lambda) is the eigenvalue.

Let’s keep in mind that the goal is to find both λ (the eigenvalue) and 𝑣 (the eigenvector).

Step 2: Rearrange the equation

To proceed with our goal, we need to solve for λ. So, we will first rearrange the equation to make it easier to work with by moving the right-hand side to the left-hand side with an inverse sign:

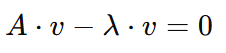
Now we can factor out the 𝑣, but since 𝐴 is a matrix and 𝑣 is a vector, we will need to multiply 𝑣 by a what is called an identity matrix, denoted as I. An identity matrix is a square matrix (with size nxn) with 1's on its diagonal and 0's elsewhere. Because of the characteristic of matrix multiplication, an identity matrix acts like the number 1 for matrices. Take, for example, this identity matrix of size 3x3:

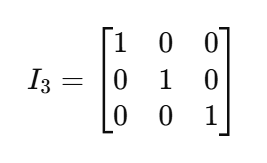
Back to our equation, if we factor out the 𝑣, and multiply it by I, the result would be the following:

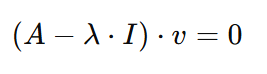
Step 3: Set up the determinant

To solve for the equation that we arrived to, either the eigenvector 𝑣 must be zero, or else the eigenvector would be equal to whatever is 𝐴 −λ⋅I. And now is the suitable time to say one more thing about eigenvectors- they cannot be equal to zero. Therefore, 𝐴 −λ⋅I must be equal to zero. But since lambda is the unknown, we can get the left-hand side of the equation to be equal to its right-hand side if we take the determinant of the 𝐴 −λ⋅I. So, we arrive at the following equation:

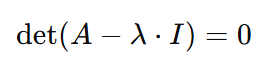
Here we have arrived at the characteristic equation. Solving the characteristic equation can give us both the eigenvalues λ and the eigenvector 𝑣, and shown in the remaining steps.

Step 4: Solve for eigenvalues

Assuming that we have the following matrix 𝐴:

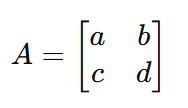
By substituting 𝐴 with the actual matrix in the characteristic equation, the equation becomes:

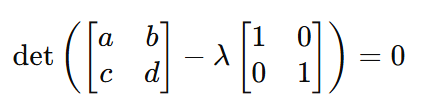
And therefore:

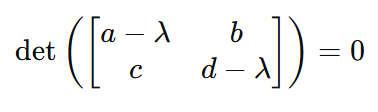
And therefore once again:

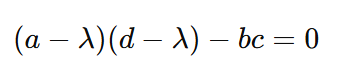
From this much simpler form of equation, we can calculate the values of the eigenvalues λ by only substituting the values of the matrix.

Step 5: Solve for eigenvectors 𝑣

By getting the eigenvalues λ, what remains is to get the eigenvectors 𝑣. We can do this by returning to this previous form of the equation:

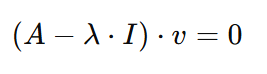
Now, if we substitute 𝐴, λ, and I with their values, we can easily calculate the value of eigenvector 𝑣.

Numerical computation methods

As we have seen, the complexity of calculating the eigenvectors and eigenvalues largely depends on the size of the matrix. In our example, we used a simple 2x2 𝐴 matrix. But we can’t practically find the eigenvectors and eigenvalues in this way when the matrices get much larger, such as when they have hundreds or thousands of rows and columns. In this case, we use programming languages like Python and R, which use numerical computation methods as opposed to symbolic methods. Some of the techniques used include:

1. QR Algorithm: This is a common method for finding eigenvalues. It involves a sequence of matrix factorizations (QR factorizations) to iteratively converge to the eigenvalues.
2. Cholesky or LU Decomposition: For certain kinds of matrices (e.g., symmetric or positive definite matrices), specialized methods like Cholesky or LU decomposition may be used for more efficient computation.
3. Balancing and Scaling: To improve numerical stability, R and Python will often scale and balance matrices before performing calculations.

Considerations in Data Science and Machine Learning

Eigenvectors and eigenvalues are essential in many applications, including the following:

• Image Processing: They are used in facial recognition and image classification.
• Natural Language Processing (NLP): Eigenvectors and eigenvalues are used in topic modeling and word embeddings.
• Recommendation Systems: As in collaborative and content-based filtering, where dimensionality reduction can improve the accuracy of the recommendation systems.
• Spectral Clustering: Eigenvectors and eigenvalues are also a founding component of spectral clustering, which is a method that groups data points by looking at their connections in a graph, using information from the structure of the data instead of just distance that has several practical applications, such as in image processing.
• Principal Component Analysis: PCA is a dimensionality reduction technique common in machine learning. With PCA, with find the eigenvectors of the standardized covariance matrix and sort them by eigenvalue. 

We said that eigenvalues can be any real or complex number. That means that the eigenvalue can be zero, and it can also mean that we can have multiple eigenvalues in the analyzed matrix that are equal. These two cases are considered two errors that may arise within any eigen analysis. Let’s have a look at each.

Zero eigenvalue problem

A zero eigenvalue is a problem because it means that the transformation of its correspondent eigenvector resulted in a zero vector, which can be imagined as a single point in space with no magnitude and, therefore, explains no variance in the dataset. The problem can be handled with regularization techniques, like ridge regression (Tikhonov regularization), or with removing collinear features (aka dimensionality reduction), which naturally happens in a PCA algorithm. Therefore, the zero eigenvalue is not a problem for PCA, and, in fact, PCA can be one solution for it. However, for other machine learning algorithms that involve solving linear systems, like linear, ridge, and lasso regressions, the zero eigenvalue problem should be handled beforehand.

Degenerate eigenvalues

When multiple eigenvalues have the same value, they are called degenerates, and they are a problem in data science, especially from a practical point of view in PCA and spectral clustering. In PCA, if multiple eigenvectors have identical eigenvalues, it means that these eigenvectors capture the same amount of variance in the dataset, and therefore, the choice of k principal components becomes problematic. In spectral clustering, where eigenvalues of the similarity matrix are used to group data points, degenerate eigenvalues can indicate that the data points are equally similar in multiple dimensions, which makes it difficult to determine which dimensions or eigenvectors should be used to separate the clusters.

Eigenvectors, Eigenvalues, and Eigendecomposition

Any discussion of eigenvectors and eigenvalues would not be complete without also talking about eigendecomposition. Eigendecomposition is the process of decomposing a square matrix A into its eigenvectors and eigenvalues. For a matrix that can be decomposed, it can be expressed as:

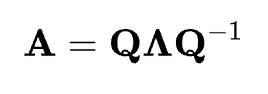
Eigendecomposition tells us that the matrix A can be expressed as the product of its eigenvectors matrix Q, a diagonal matrix Λ of its eigenvalues, and the inverse of the eigenvectors matrix Q^-1. These matrices, when multiplied together in matrix multiplication, will reconstruct the original matrix A. Eigendecomposition is important because it provides a way to understand and simplify complex linear transformations, providing insights into system behavior, and it also simplifies many computations. 

Conclusion

In this article, we have seen what eigenvectors and eigenvalues are and how they are extremely relevant to data science and machine learning. We also went through how they are mathematically calculated, as well as what errors may arise when trying to find eigenvectors and eigenvalues.

In addition to the Linear Algebra in R course and the SciPy tutorial on vectors and arrays, if you are serious about eigenvectors and eigenvalues and their applications in machine learning, try our Machine Learning Scientist with Python career track and become an expert in supervised and unsupervised learning, including, of course, dimensionality reduction.