Sklearn Lineare Regression: Ein vollständiger Leitfaden mit Beispielen

Die lineare Regression ist eine grundlegende Technik in der Statistik und im maschinellen Lernen, die dabei hilft, die Beziehung zwischen Variablen zu modellieren. Vereinfacht ausgedrückt, ermöglicht sie uns, ein Ergebnis auf der Grundlage eines oder mehrerer Einflussfaktoren vorherzusagen. Sie findet breite Anwendung in der Immobilienpreisgestaltung, der Absatzprognose, der Risikobewertung und vielen anderen Bereichen.

In diesem Tutorial lernen wir die lineare Regression in scikit-learn kennen. Wir erklären, wie sie funktioniert, warum sie nützlich ist und wie man sie mit scikit-learn implementiert. Am Ende wirst du in der Lage sein, ein lineares Regressionsmodell zu erstellen und auszuwerten, um datengestützte Vorhersagen zu treffen.

Streudiagramm von Hauspreis und Anzahl der Zimmer

Lineare Regression und maschinelles Lernen

Abgesehen von ihrer unmittelbaren Nützlichkeit bei der Ermittlung von Hauspreisen spielt die lineare Regression auch beim maschinellen Lernen eine wichtige Rolle.

• Es ist ein grundlegendes Modell für das Verständnis fortgeschrittener Techniken wie logistische Regression, neuronale Netze und Support Vector Machines.
• Es ist schnell zu trainieren und daher ideal für Rapid Prototyping.
• Sie dient auch als Basis für einen Vergleich. Wenn fortschrittlichere Modelle diese nicht deutlich übertreffen, ist ihre zusätzliche Komplexität möglicherweise nicht gerechtfertigt.
• Im Gegensatz zu anderen Techniken (z. B. Deep Learning) ist sie leicht zu interpretieren.
• Sie kann bei der Auswahl der Merkmale helfen, indem sie die nützlichsten Prädiktoren identifiziert.

Trotz ihrer Einfachheit bleibt die lineare Regression aufgrund ihrer Effizienz, Interpretierbarkeit und Vielseitigkeit ein unverzichtbares Werkzeug beim maschinellen Lernen.

Lineare Regression und die Scikit-Learn-Bibliothek

Mit der scikit-learn-Bibliothek lässt sich die lineare Regression leicht umsetzen. Diese Bibliothek hat viele Vorteile.

• Es hat eine einheitliche Schnittstelle. Der Code, der für die Implementierung verschiedener ML-Algorithmen benötigt wird, ist ähnlich.
• Der Code ist einfach und enthält keine komplexen mathematischen oder implementierungsbezogenen Details. Um zum Beispiel ein Modell an die Trainingsdaten anzupassen, benutze einfach die Zeile model.fit(X_train, y_train).
• Sie bietet einen einfachen Zugang zu den Modellkoeffizienten.
• Es bietet integrierte Metriken zur Bewertung der Modellleistung.
• Es ist einfach, die lineare Regression (oder jeden anderen ML-Algorithmus) mit Vorverarbeitungsschritten wie der Skalierung und der Auswahl von Merkmalen in Pipeline zu integrieren.

Wenn du scikit-learn noch nicht kennst, kannst du in unserem Kurs über Maschinelles Lernen mit scikit-learn eine praktische Einführung in die Python-Bibliothek erhalten. 

Lineare Regression verstehen

Wie wir gesehen haben, werden die Daten bei der einfachen linearen Regression mit einer "Best-Fit-Linie" modelliert. Die Formel für diese Zeile lautet: 

wobei m die Steigung der Linie und b der Achsenabschnitt ist.

Die "multiple lineare Regression" verallgemeinert den Fall von einem Prädiktor auf mehrere Prädiktoren (Anzahl der Zimmer, Nähe zum Meer, mittleres Einkommen der Nachbarschaft). Die Formel wird verallgemeinert zu: 

Dabei ist jedes _xi eine unabhängige Variable und das zugehörige _bi ist ihr Koeffizient. In drei Dimensionen wird die Linie zu einer Ebene verallgemeinert. In höheren Dimensionen wird die Ebene zu einer "Hyperebene".

Wie interpretieren wir die Koeffizienten und den Achsenabschnitt? Der Achsenabschnitt ist der vorhergesagte Wert von y, wenn alle unabhängigen Variablen 0 sind, oder anders ausgedrückt, der Basiswert der abhängigen Variable, wenn die Prädiktoren keinen Beitrag leisten. Jeder Koeffizient _bi steht für die Veränderung der abhängigen Variable y bei einer Veränderung von _xi um eine Einheit, wobei alle anderen unabhängigen Variablen konstant bleiben.

Einrichten der Umgebung

Die Installation von scikit-learn ist einfach. Verwende einfach den Befehl pip install scikit-learn. Wenn du eine bestimmte Version installieren möchtest, z.B. 1.2.2, dann ändere den Befehl, um die Version anzugeben: pip install scikit-learn==1.2.2. Wenn du Anaconda benutzt, sollte scikit-learn bereits installiert sein. Wenn du es aus irgendeinem Grund trotzdem installieren musst, wenn du die Anaconda-Distribution verwendest, benutze den Befehl conda install scikit-learn.

Bei der Verwendung von scikit-learn sind mehrere Bibliotheken entweder notwendig oder empfehlenswert. Die Bibliothek numpy wird für die Speicherung von Merkmalen und Beschriftungen benötigt. Die Bibliothek pandas wird zum Laden, Vorverarbeiten und Erkunden von Datensätzen empfohlen .

Wenn du scikit-learn benutzt, verwendest du wahrscheinlich schon Pandas für deine Datenvorbereitung. Um deine Ergebnisse darzustellen, wirst du wahrscheinlich matplotlib oder seaborn oder beides verwenden. Jede dieser Bibliotheken kann mit pip install installiert werden, ähnlich wie im obigen Beispiel. Du kannst sogar mehrere Bibliotheken mit einem Befehl installieren:

pip install scikit-learn numpy pandas matplotlib seaborn.

Lineare Regression in Sklearn implementieren

Bevor wir den Datensatz laden, lass uns die üblichen Verdächtigen importieren.

# Import libraries.
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns

Laden des Datensatzes

Nehmen wir den bekannten kalifornischen Wohnungsdatensatz.

# Read in California housing dataset.
from sklearn.datasets import fetch_california_housing


housing = fetch_california_housing()

Aufbereitung der Daten

Teilen wir die Daten in Trainings- und Testgruppen auf. Wir importieren die Methode train_test_split() von sklearn.model_selection und rufen sie auf, indem wir einen Prozentsatz der Testmenge und eine random_state angeben . Wir verwenden auch eine einfache lineare Regression, indem wir das Merkmal verwenden, das der durchschnittlichen Anzahl der Zimmer entspricht.

# Import train_test_split.
from sklearn.model_selection import train_test_split


# Create features X and target y.
X = pd.DataFrame(housing.data, columns=housing.feature_names)[["AveRooms"]]
y = housing.target  # Median house value in $100,000s


# Split the dataset into training (80%) and testing (20%) sets.
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

Jetzt, wo wir die Daten in Test- und Trainingsdatensätze aufgeteilt haben, können wir die Merkmale standardisieren. Dieses Verfahren stellt sicher, dass alle Variablen auf der gleichen Skala liegen, was die Modellleistung und die numerische Stabilität verbessern kann.

# Import StandardScaler.
from sklearn.preprocessing import StandardScaler

# Instantiate StandardScaler.
scaler = StandardScaler()

# Fit and transform training data.
X_train_scaled = scaler.fit_transform(X_train)

# Also transform test data.
X_test_scaled = scaler.transform(X_test)

In diesem Code ist StandardScaler ein Werkzeug zur Datenvorverarbeitung, das verwendet wird, um den Mittelwert zu entfernen und die Merkmale auf eine Einheitsvarianz zu skalieren. So kannst du verhindern, dass bestimmte Merkmale aufgrund von Größenunterschieden das Modell dominieren.

Der Skalierer wird mit der Methodefit_transform() an die Trainingsdaten angepasst . Die Testdaten werden dann separat mit der Methode transform() umgewandelt, um sicherzustellen, dass sie mit denselben Faktoren wie die Trainingsdaten skaliert werden, um Datenverluste zu vermeiden.

Training des linearen Regressionsmodells

Um ein lineares Regressionsmodell zu erstellen, importiere LinearRegression() von sklearn.linear_model. Rufe sie auf und weise sie einer Variablen zu.

# Import LinearRegression.
from sklearn.linear_model import LinearRegression


# Instantiate linear regression model.
model = LinearRegression()

Die Anpassung des Modells an die Trainingsdaten ist ganz einfach.

# Fit the model to the training data.
model.fit(X_train_scaled, y_train)

Vorhersagen treffen

Jetzt, wo wir unser Modell trainiert haben, machen wir Vorhersagen für die Testmenge.

# Make predictions on the testing data.
y_pred = model.predict(X_test_scaled)

Bewertung der Modellleistung

Nachdem wir nun Vorhersagen für die Testmenge gemacht haben, müssen wir wissen, wie gut sie mit der Realität übereinstimmen. Es gibt verschiedene Metriken, um die Leistung eines Regressionsalgorithmus zu bewerten. Einige der gängigsten sind das Bestimmtheitsmaß (^R2), der mittlere quadratische Fehler (MSE) und der mittlere quadratische Fehler (RMSE).

Das Bestimmtheitsmaß, auch^R2 genannt, misst, wie gut ein Regressionsmodell die Variabilität der Zielvariablen erklärt. Mit anderen Worten: Sie gibt an, wie viel der Variabilität der Zielvariablen durch die Prädiktoren erklärt wird, was als Anpassungsgüte bezeichnet wird.

Um das besser zu verstehen, schauen wir uns die Formel an:

wobei yIst die tatsächlichen Werte der Zielvariablen, yVorhersage die vom Modell vorhergesagten Werte und ȳ der Mittelwert der tatsächlichen Werte ist. Diese Formel hilft uns zu verstehen, wie viel Varianz in der Zielvariable durch das Modell erklärt wird. Der Nenner steht für die Gesamtvarianz der Daten, während der Zähler die unerklärte Varianz nach Anwendung des Regressionsmodells darstellt. Der Quotient gibt also den Prozentsatz der Varianz an, der durch das Modell erklärt wird.

Wie interpretieren wir^R2?

• ^R2 = 1: Das Modell erklärt die gesamte Varianz der Zielvariable perfekt. 
• ^R2 = 0: Das Modell erklärt keinen Teil der Varianz; die Vorhersagen sind nicht besser als der Mittelwert. 
• R² < 0: Das Modell schneidet schlechter ab als die Verwendung des Mittelwerts, was auf eine schlechte Anpassung hindeutet.

Einige wichtige Überlegungen, die du beachten solltest.

• Ein höherer^R2-Wert ist nicht immer besser. Ein hohes^R2 kann auf eine Überanpassung hinweisen, insbesondere bei komplexen Modellen. 
• Wenn du mehr Funktionen hinzufügst, kann das^R2 künstlich erhöht werden, sodass ein höherer Wert nicht unbedingt besser ist.
• Bei der multiplen Regression verwendest du das bereinigte^R2, das die Anzahl der Prädiktoren berücksichtigt und irreführende Verbesserungen durch unnötige Variablen vermeidet.

Die Bewertung der Modellleistung mithilfe des Bestimmtheitsmaßes ist mit scikit-learn einfach.

# Import metrics.
from sklearn.metrics import mean_squared_error, r2_score


# Calculate and print R^2 score.
r2 = r2_score(y_test, y_pred)
print(f"R-squared: {r2:.4f}")

R-squared: 0.0138

Andere häufig verwendete Messgrößen sind der mittlere quadratische Fehler (MSE) und der mittlere quadratische Fehler (RMSE). Diese Metriken messen, wie weit die Vorhersagen eines Modells von den tatsächlichen Werten abweichen.

MSE berechnet die durchschnittliche quadratische Differenz zwischen tatsächlichen und vorhergesagten Werten: 

für die Gesamtzahl der Beobachtungen n. Da die Fehler vor der Mittelwertbildung quadriert werden, werden größere Fehler stärker bestraft als kleinere, wodurch der MSE empfindlich auf Ausreißer reagiert. Ein geringerer MSE bedeutet eine bessere Modellanpassung.

Um dieses Problem zu lösen, wird der RMSE verwendet, der einfach die Quadratwurzel des MSE ist. Da der RMSE in denselben Einheiten wie die Zielvariable angegeben wird, ist er ein besser interpretierbares Maß dafür, wie weit die Vorhersagen im Durchschnitt abweichen.

Die Berechnung von MSE und RMSE ist mit Scikit-Learn einfach.

# Calculate and print MSE.
mse = mean_squared_error(y_test, y_pred)
print(f"Mean squared error: {mse:.4f}")


# Calculate and print RMSE.
rmse = mse ** 0.5
print(f"Root mean squared error: {rmse:.4f}")

Mean squared error: 1.2923
Root mean squared error: 1.1368

Arbeiten mit multipler linearer Regression in scikit-learn

Lass uns das Modell noch einmal mit allen verfügbaren Merkmalen durchführen, nicht nur mit der durchschnittlichen Anzahl der Zimmer. Erwartest du bessere oder schlechtere Ergebnisse?

# Uses all features.
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.datasets import fetch_california_housing
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error, r2_score


# Load data set.
housing = fetch_california_housing()


# Split into X, y.
X = pd.DataFrame(housing.data, columns=housing.feature_names)
y = housing.target  # Median house value in $100,000s
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)


# Scale the data.
scaler = StandardScaler()


X_train_scaled = scaler.fit_transform(X_train)
X_test_scaled = scaler.transform(X_test)


# Create model and fit it to the training data.
model = LinearRegression()
model.fit(X_train_scaled, y_train)


# Make predictions.
y_pred = model.predict(X_test_scaled)


# Calculate and print errors.
r2 = r2_score(y_test, y_pred)
print(f"R-squared: {r2:.4f}")


mse = mean_squared_error(y_test, y_pred)
print(f"Mean squared error: {mse:.4f}")


rmse = mse ** 0.5
print(f"Root mean squared error: {rmse:.4f}")

R-squared: 0.5758
Mean squared error: 0.5559
Root mean squared error: 0.7456

Wir sehen, dass die Ergebnisse um einiges besser sind als bei der Verwendung von nur einem Merkmal. Das wirft jedoch die Frage auf, ob wir alle Funktionen brauchen. Sind einige Merkmale wichtiger als andere? Die Auswahl der wichtigsten Merkmale aus dem Datensatz wird als Merkmalsauswahl bezeichnet.

Die Auswahl der Merkmale ist aus mehreren Gründen wichtig.

• Reduziert die Überanpassung. Weniger Merkmale bedeuten weniger Komplexität und verringern das Risiko einer Überanpassung.
• Verbessert die Genauigkeit. Das Entfernen von irrelevanten oder redundanten Merkmalen hilft dem Modell, sich auf sinnvolle Muster zu konzentrieren.
• Verbessert die Interpretierbarkeit. Macht Modelle leichter verständlich, indem es die wichtigsten Faktoren hervorhebt.
• Beschleunigt die Ausbildung. Die Reduzierung der Anzahl der Merkmale verringert die Rechenzeit und den Speicherbedarf.

Wenn mehrere Merkmale hoch korreliert sind, sind sie redundant, d. h., sie liefern dem Modell im Wesentlichen dieselben Informationen. Diese Situation wird als Multikollinearität bezeichnet. Multikollinearität wirkt sich zwar nicht immer auf die Genauigkeit von Vorhersagemodellen aus, erschwert aber die Merkmalsauswahl und -interpretation, insbesondere bei der linearen Regression und ähnlichen Modellen.

Der Varianz-Inflations-Faktor (VIF) ist eine Metrik, die verwendet wird, um Multikollinearität zwischen Prädiktoren zu erkennen. Für jeden Prädiktor wird der VIF wie folgt berechnet: 

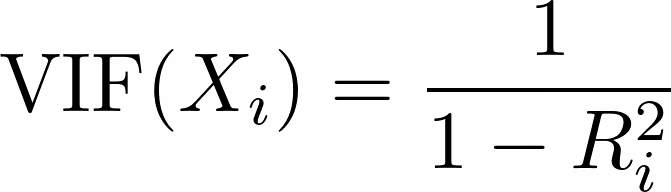
Dabei ist ^Ri2 der ^R2-Wert, der sich ergibt, wenn der Prädiktor _Xi gegen alle anderen Prädiktoren im Modell regressiert wird. Ein höherer VIF bedeutet, dass der Prädiktor stark mit anderen Variablen korreliert ist.

• VIF = 1: keine Multikollinearität (ideales Szenario).
• VIF < 5: geringe bis mittlere Multikollinearität (im Allgemeinen akzeptabel).
• VIF > 5: hohe Multikollinearität (erwäge das Entfernen oder Kombinieren korrelierter Variablen).
• VIF > 10: starke Multikollinearität (deutet stark auf Variablenredundanz hin).

# Import libraries.
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
from sklearn.datasets import fetch_california_housing
from statsmodels.stats.outliers_influence import variance_inflation_factor


# Load the dataset.
housing = fetch_california_housing()
X = pd.DataFrame(housing.data, columns=housing.feature_names)


# Compute the correlation matrix.
corr_matrix = X.corr()


# Identify pairs of features with high collinearity (correlation > 0.8 or < -0.8).
high_corr_features = [(col1, col2, corr_matrix.loc[col1, col2])
                     for col1 in corr_matrix.columns
                     for col2 in corr_matrix.columns
                     if col1 != col2 and abs(corr_matrix.loc[col1, col2]) > 0.8]


# Convert to a DataFrame for better visualization.
collinearity_df = pd.DataFrame(high_corr_features, columns=["Feature 1", "Feature 2", "Correlation"])
print("\nHighly Correlated Features:\n", collinearity_df)


# Compute Variance Inflation Factor (VIF) for each feature.
vif_data = pd.DataFrame()
vif_data["Feature"] = X.columns
vif_data["VIF"] = [variance_inflation_factor(X.values, i) for i in range(X.shape[1])]


# Print VIF values.
print("\nVariance Inflation Factor (VIF) for each feature:\n", vif_data)

   Highly Correlated Features:
       Feature 1  Feature 2  Correlation
   0   AveRooms  AveBedrms     0.847621
   1  AveBedrms   AveRooms     0.847621
   2   Latitude  Longitude    -0.924664
   3  Longitude   Latitude    -0.924664
  
   Variance Inflation Factor (VIF) for each feature:
          Feature         VIF
   0      MedInc   11.511140
   1    HouseAge    7.195917
   2    AveRooms   45.993601
   3   AveBedrms   43.590314
   4  Population    2.935745
   5    AveOccup    1.095243
   6    Latitude  559.874071
   7   Longitude  633.711654

Lass uns AveBedrms aus dem Modell entfernen.

# Import libraries.
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.datasets import fetch_california_housing
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error, r2_score


# Load California housing dataset.
housing = fetch_california_housing()


# Create DataFrame and remove "AveBedrms" feature.
X = pd.DataFrame(housing.data, columns=housing.feature_names).drop(columns=["AveBedrms"])
y = housing.target  # Median house value in $100,000s


# Split data into training and testing sets.
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)


# Scale the data (Standardization).
scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train)
X_test_scaled = scaler.transform(X_test)


# Create a linear regression model and train it.
model = LinearRegression()
model.fit(X_train_scaled, y_train)


# Make predictions on the test set.
y_pred = model.predict(X_test_scaled)


# Calculate performance metrics.
r2 = r2_score(y_test, y_pred)
mse = mean_squared_error(y_test, y_pred)
rmse = np.sqrt(mse)
# Print evaluation metrics
print(f"R-squared: {r2:.4f}")
print(f"Mean squared error: {mse:.4f}")
print(f"Root mean squared error: {rmse:.4f}")

R-squared: 0.5823
Mean squared error: 0.5473
Root mean squared error: 0.7398

Die Ergebnisse sind (geringfügig) verbessert.

Extrahieren von Modell-Insights

Die Erstellung eines Regressionsmodells ist nur der erste Schritt; genauso wichtig ist es, seine Ergebnisse zu verstehen. Durch die Analyse der Koeffizienten des Modells können wir feststellen, welche Merkmale den größten Einfluss auf die Vorhersagen haben.

Regressionskoeffizienten verstehen

Sobald ein lineares Regressionsmodell trainiert ist, können die Koeffizienten mit model.coef_ abgerufen werden. Das Intercept kann über model.intercept_ abgerufen werden.

Sobald ein lineares Regressionsmodell mit LinearRegression() trainiert wurde, kann man auf die Koeffizienten mit model.coef_ und auf den Achsenabschnitt mit model.intercept_.

print("Intercept:", model.intercept_)


coeff_df = pd.DataFrame({"Feature": X.columns, "Coefficient": model.coef_})
print("\nFeature Coefficients:\n", coeff_df)

   Intercept: 2.0719469373788777  

   Feature Coefficients:

         Feature  Coefficient

   0     MedInc     0.725747

   1   HouseAge     0.121519

   2   Latitude    -0.943105

   3  Longitude    -0.900735

Zusammenfassung der Modellergebnisse

Da Scikit-Learn keine eingebaute summary() Methode wie Statsmodels bietet, können wir die Wichtigkeit jedes Merkmals mithilfe von Regressionskoeffizienten manuell extrahieren und visualisieren. Merkmale mit größeren absoluten Koeffizienten haben einen stärkeren Einfluss auf die Zielvariable. Betrachte den folgenden Code.

# Sort dataframe by coefficients.
coef_df_sorted = coef_df.sort_values(by="Coefficient", ascending=False)


# Create plot.
plt.figure(figsize=(8,6))
plt.barh(coef_df["Feature"], coef_df_sorted["Coefficient"], color="blue")
plt.xlabel("Coefficient Value")
plt.ylabel("Feature")
plt.title("Feature Importance (Linear Regression Coefficients)")
plt.show()

Diagramm der Merkmalswichtigkeit basierend auf den Koeffizientenwerten

Jetzt wollen wir die Residuen und die Regressionsanpassung visualisieren.

# Compute residuals.
residuals = y_test - y_pred


# Create plots.
plt.figure(figsize=(12,5))


# Plot 1: Residuals Distribution.
plt.subplot(1,2,1)
sns.histplot(residuals, bins=30, kde=True, color="blue")
plt.axvline(x=0, color='red', linestyle='--')
plt.title("Residuals Distribution")
plt.xlabel("Residuals (y_actual - y_predicted)")
plt.ylabel("Frequency")


# Plot 2: Regression Fit (Actual vs Predicted).
plt.subplot(1,2,2)
sns.scatterplot(x=y_test, y=y_pred, alpha=0.5)
plt.plot([min(y_test), max(y_test)], [min(y_test), max(y_test)], color='red', linestyle='--')  # Perfect fit line
plt.title("Regression Fit: Actual vs Predicted")
plt.xlabel("Actual Prices (in $100,000s)")
plt.ylabel("Predicted Prices (in $100,000s)")


# Show plots.
plt.tight_layout()
plt.show()

Diagramme zur Visualisierung von Residuen und Regressionsanpassung

Die Verteilung der Residuen (linkes Diagramm) sollte um Null zentriert sein, was bedeutet, dass die Fehler zufällig verteilt sind. Wenn die Residuen einer Normalverteilung folgen, passt das Modell gut, aber wenn es eine Schräglage oder einen Trend gibt, kann das auf systematische Fehler hindeuten. Die Regressionsanpassung (rechte Grafik) vergleicht die tatsächlichen mit den vorhergesagten Werten, wobei die rote gestrichelte Linie eine perfekte Anpassung darstellt. Wenn die Punkte genau der Linie folgen, sind die Vorhersagen genau, aber wenn ein Muster (z. B. eine Kurve) auftaucht, ist die Beziehung möglicherweise nicht wirklich linear. 

Diese Visualisierungen helfen dabei, eine Über- oder Unteranpassung zu diagnostizieren, zeigen Muster in den Residuen auf, die auf fehlende Beziehungen hindeuten, und liefern eine klare Bewertung der Effektivität des Modells.

Anwendungen in der realen Welt

Die lineare Regression wird in vielen Branchen zur Vorhersage und Entscheidungsfindung eingesetzt. In der Immobilienbranche schätzt sie die Hauspreise anhand von Faktoren wie Größe und Lage. 

Vertrieb und Marketing nutzen es für die Nachfrageprognose und die Budgetoptimierung, während das Gesundheitswesen es zur Bewertung von Krankheitsrisiken einsetzt. Im Finanzwesen hilft sie bei der Vorhersage von Aktienkursen und bei der Kreditwürdigkeitsprüfung, und in der Produktion hilft sie bei der Qualitätskontrolle und der Vorhersage von Fehlern. 

Wann wird die lineare Regression verwendet?

• Merkmale und die Zielvariable stehen in einem linearen Verhältnis zueinander.
• Interpretierbarkeit und Einfachheit zählen mehr als komplexe Modellierung.
• Die Daten erfordern ein minimales Feature Engineering.

Wann man die lineare Regression nicht verwenden sollte

• Die Beziehung zwischen dem Ziel und den Merkmalen ist komplex und nicht-linear.
• Die Daten sind stark korreliert.
• Die Daten enthalten Ausreißer, die nicht entfernt werden können. In diesem Fall musst du eventuell Daten umwandeln oder Strategien anwenden, um ihre Auswirkungen zu mildern.

Fazit

Die lineare Regression ist nach wie vor eine der grundlegendsten und am häufigsten verwendeten Techniken des maschinellen Lernens und der statistischen Modellierung. Trotz ihrer Einfachheit ist sie ein mächtiges Werkzeug, um Beziehungen zwischen Variablen zu verstehen und Vorhersagen in verschiedenen realen Anwendungen zu treffen.

Hier sind die wichtigsten Erkenntnisse aus dem Tutorium:

• Vielseitig einsetzbar. Die lineare Regression liefert wertvolle Erkenntnisse für verschiedene Branchen und Problembereiche.
• Interpretierbar.  Im Gegensatz zu komplexen Blackbox-Modellen bietet die lineare Regression klare, auf Koeffizienten basierende Interpretationen und ist daher leicht zu verstehen und zu erklären.
• Auswahl der Merkmale. Durch die richtige Auswahl von Merkmalen und die Berücksichtigung von Multikollinearität wird sichergestellt, dass die Modelle genau, stabil und zuverlässig bleiben. 

Weitere Informationen zur Python-String-Interpolation findest du in den Ressourcen von DataCamp.

• Einfache lineare Regression: Alles, was du wissen musst - Tutorial
• Wie man eine lineare Regression in R durchführt - Tutorial
• Lineare Regression in Excel: Ein umfassender Leitfaden für Einsteiger - Tutorial
• Einführung in die Regression in R - Kurs
• Überwachtes Lernen mit scikit-learn - Kurs
• Scikit-Learn Spickzettel: Python Machine Learning - Spickzettel
• Die logistische Regression in Python verstehen - Tutorial