Sklearn Regresión lineal: Una guía completa con ejemplos

La regresión lineal es una técnica fundamental en estadística y aprendizaje automático que ayuda a modelizar la relación entre variables. En términos sencillos, nos permite predecir un resultado basándonos en uno o varios factores influyentes. Se aplica ampliamente en la fijación de precios inmobiliarios, la previsión de ventas, la evaluación de riesgos y muchos otros campos.

En este tutorial, exploraremos la regresión lineal en scikit-learn, cubriendo cómo funciona, por qué es útil y cómo implementarla utilizando scikit-learn. Al final, serás capaz de construir y evaluar un modelo de regresión lineal para hacer predicciones basadas en datos.

Gráfico de dispersión del precio de la vivienda frente al número de habitaciones

Regresión lineal y aprendizaje automático

Más allá de su utilidad inmediata para determinar el precio de la vivienda, la regresión lineal desempeña un papel importante en el aprendizaje automático.

• Es un modelo básico para comprender técnicas más avanzadas como la regresión logística, las redes neuronales y las máquinas de vectores de soporte.
• Se entrena rápidamente, por lo que es ideal para la creación rápida de prototipos.
• También sirve como base de comparación. Si los modelos más avanzados no lo superan significativamente, puede que su complejidad añadida no esté justificada.
• A diferencia de algunas técnicas (como el aprendizaje profundo), es fácilmente interpretable.
• Puede ayudar en la selección de características, identificando los predictores más útiles.

A pesar de su simplicidad, la regresión lineal sigue siendo una herramienta indispensable en el aprendizaje automático debido a su eficacia, interpretabilidad y versatilidad.

Regresión lineal y la biblioteca scikit-learn

La biblioteca scikit-learn facilita la aplicación de la regresión lineal. Esta biblioteca tiene muchas ventajas.

• Tiene una interfaz coherente. El código necesario para aplicar los distintos algoritmos de ML es similar.
• El código es sencillo, y se han eliminado los complejos detalles matemáticos y de implementación. Por ejemplo, para ajustar un modelo a los datos de entrenamiento, basta con utilizar la línea model.fit(X_train, y_train).
• Facilita el acceso a los coeficientes del modelo.
• Proporciona métricas integradas para evaluar el rendimiento del modelo.
• Es fácil integrar la regresión lineal (o cualquier otro algoritmo de ML) con pasos de preprocesamiento, como el escalado y la selección de características, utilizando Pipeline.

Si eres nuevo en scikit-learn, puedes consultar nuestro curso sobre Aprendizaje automático con scikit-learn para obtener una introducción práctica a la biblioteca Python. 

Comprender la regresión lineal

Como hemos visto, en la regresión lineal simple, los datos se modelizan mediante una "recta de mejor ajuste". La fórmula de esta línea es 

donde m es la pendiente de la recta y b es la intercepción.

La "regresión lineal múltiple" generaliza el caso de un predictor a varios predictores (número de habitaciones, proximidad al mar, renta media del barrio). La fórmula se generaliza a 

donde cada _xi es una variable independiente y el _bi correspondiente es su coeficiente. En tres dimensiones, la línea se generaliza a un plano. En dimensiones superiores, el plano se convierte en un "hiperplano".

¿Cómo interpretamos los coeficientes y el intercepto? El intercepto es el valor previsto de y cuando todas las variables independientes son 0, o dicho de otro modo, es el valor de referencia de la variable dependiente cuando no hay contribución de los predictores. Cada coeficiente _bi representa el cambio en la variable dependiente y para un cambio de una unidad en _xi, manteniendo constantes todas las demás variables independientes.

Configurar el entorno

Instalar scikit-learn es fácil. Sólo tienes que utilizar el comando pip install scikit-learn. Si quieres instalar una versión concreta, por ejemplo 1.2.2, modifica el comando para incluir la versión: pip install scikit-learn==1.2.2. Si utilizas Anaconda, scikit-learn ya debería estar instalado. Si por alguna razón sigues necesitando instalarlo cuando utilizas la distribución Anaconda, utiliza el comando conda install scikit-learn.

Varias bibliotecas son necesarias o recomendables cuando se utiliza scikit-learn. La biblioteca numpy es necesaria para almacenar características y etiquetas. Se recomienda la biblioteca pandas para cargar, preprocesar y explorar conjuntos de datos .

Si utilizas scikit-learn, lo más probable es que ya estés utilizando pandas para la preparación de tus datos. Para trazar tus resultados, es probable que utilices matplotlib o seaborn o ambos. Cualquiera de estas bibliotecas puede instalarse mediante pip install, de forma similar al ejemplo anterior. Incluso puedes instalar varias bibliotecas con un solo comando:

pip install scikit-learn numpy pandas matplotlib seaborn.

Implementación de la regresión lineal en sklearn

Antes de cargar el conjunto de datos, vamos a importar los sospechosos habituales.

# Import libraries.
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns

Cargar el conjunto de datos

Utilicemos el conocido conjunto de datos sobre vivienda de California.

# Read in California housing dataset.
from sklearn.datasets import fetch_california_housing


housing = fetch_california_housing()

Preparación de los datos

Dividamos los datos en conjuntos de entrenamiento y de prueba. Importamos el método train_test_split() de sklearn.model_selection, y luego lo invocamos, especificando un porcentaje del conjunto de pruebas, y un random_state. También utilizaremos la regresión lineal simple, utilizando la característica correspondiente al número medio de habitaciones.

# Import train_test_split.
from sklearn.model_selection import train_test_split


# Create features X and target y.
X = pd.DataFrame(housing.data, columns=housing.feature_names)[["AveRooms"]]
y = housing.target  # Median house value in $100,000s


# Split the dataset into training (80%) and testing (20%) sets.
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

Ahora que hemos dividido los datos en conjuntos de prueba y de entrenamiento, vamos a normalizar las características. Este proceso garantiza que todas las variables estén en la misma escala, lo que puede mejorar el rendimiento del modelo y la estabilidad numérica.

# Import StandardScaler.
from sklearn.preprocessing import StandardScaler

# Instantiate StandardScaler.
scaler = StandardScaler()

# Fit and transform training data.
X_train_scaled = scaler.fit_transform(X_train)

# Also transform test data.
X_test_scaled = scaler.transform(X_test)

En este código, StandardScaler es una herramienta de preprocesamiento de datos que se utiliza para eliminar la media y escalar los rasgos a la varianza unitaria. Esto ayuda a evitar que determinadas características dominen el modelo debido a las diferencias de escala.

El escalador se ajusta a los datos de entrenamiento mediante el métodofit_transform(). A continuación, los datos de prueba se transforman por separado utilizando el método transform() para garantizar que se escalan utilizando los mismos factores que los datos de entrenamiento, evitando la fuga de datos.

Entrenamiento del modelo de regresión lineal

Para crear un modelo de regresión lineal, importa LinearRegression() de sklearn.linear_model. Invócalo y asígnalo a una variable.

# Import LinearRegression.
from sklearn.linear_model import LinearRegression


# Instantiate linear regression model.
model = LinearRegression()

Ajustar el modelo con los datos de entrenamiento es sencillo.

# Fit the model to the training data.
model.fit(X_train_scaled, y_train)

Hacer predicciones

Ahora que hemos entrenado nuestro modelo, hacemos predicciones sobre el conjunto de pruebas.

# Make predictions on the testing data.
y_pred = model.predict(X_test_scaled)

Evaluar el rendimiento del modelo

Ahora que hemos hecho predicciones sobre el conjunto de pruebas, necesitamos saber hasta qué punto coinciden con la realidad. Existen varias métricas para evaluar el rendimiento de un algoritmo de regresión. Algunos de los más comunes son el coeficiente de determinación (^R2), el error cuadrático medio (MSE) y el error cuadrático medio (RMSE).

El coeficiente de determinación, denotado^R2, mide lo bien que un modelo de regresión explica la variabilidad de la variable objetivo. En otras palabras, cuantifica qué parte de la variabilidad de la variable objetivo explican los predictores, lo que se conoce como bondad de ajuste.

Para entenderlo mejor, veamos la fórmula:

donde yactual son los valores reales de la variable objetivo, ypredicted son los valores predichos del modelo, y ȳ es la media de los valores reales. Esta fórmula nos ayuda a comprender cuánta varianza de la variable objetivo explica el modelo. El denominador representa la varianza total de los datos, mientras que el numerador representa la varianza no explicada tras aplicar el modelo de regresión. La relación, por tanto, da el porcentaje de varianza explicada por el modelo.

¿Cómo interpretamos^R2?

• ^R2 = 1: el modelo explica perfectamente toda la varianza de la variable objetivo. 
• ^R2 = 0: el modelo no explica nada de la varianza; las predicciones no son mejores que utilizar simplemente la media. 
• R² < 0: El modelo funciona peor que utilizando simplemente la media, lo que indica un mal ajuste.

Algunas consideraciones clave a tener en cuenta.

• Un^R2 más alto no siempre es mejor. Un^R2 elevado puede indicar un ajuste excesivo, especialmente con modelos complejos. 
• Añadir más funciones puede aumentar artificialmente^R2, por lo que un valor más alto no es necesariamente mejor.
• Para la regresión múltiple, utiliza el^R2 ajustado, que tiene en cuenta el número de predictores y evita mejoras engañosas de variables innecesarias.

Evaluar el rendimiento del modelo mediante el coeficiente de determinación es fácil con scikit-learn.

# Import metrics.
from sklearn.metrics import mean_squared_error, r2_score


# Calculate and print R^2 score.
r2 = r2_score(y_test, y_pred)
print(f"R-squared: {r2:.4f}")

R-squared: 0.0138

Otras métricas utilizadas habitualmente son el error cuadrático medio (ECM) y el error cuadrático medio (ECM). Estas métricas miden cuánto se desvían las predicciones de un modelo de los valores reales.

El MSE calcula la diferencia cuadrática media entre los valores reales y los previstos: 

para el número total de observaciones n. Como los errores se elevan al cuadrado antes de promediar, los errores más grandes se penalizan más que los pequeños, lo que hace que el MSE sea sensible a los valores atípicos. Un MSE menor indica un mejor ajuste del modelo.

Para resolver este problema, se utiliza el RMSE, que no es más que la raíz cuadrada del MSE. Como el RMSE está en las mismas unidades que la variable objetivo, proporciona una medida más interpretable de cuánto se alejan las predicciones, por término medio.

Calcular el MSE y el RMSE es fácil con scikit-learn.

# Calculate and print MSE.
mse = mean_squared_error(y_test, y_pred)
print(f"Mean squared error: {mse:.4f}")


# Calculate and print RMSE.
rmse = mse ** 0.5
print(f"Root mean squared error: {rmse:.4f}")

Mean squared error: 1.2923
Root mean squared error: 1.1368

Trabajar con regresión lineal múltiple en scikit-learn

Volvamos a ejecutar el modelo utilizando todas nuestras características disponibles, no sólo el número medio de habitaciones. ¿Esperas mejores o peores resultados?

# Uses all features.
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.datasets import fetch_california_housing
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error, r2_score


# Load data set.
housing = fetch_california_housing()


# Split into X, y.
X = pd.DataFrame(housing.data, columns=housing.feature_names)
y = housing.target  # Median house value in $100,000s
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)


# Scale the data.
scaler = StandardScaler()


X_train_scaled = scaler.fit_transform(X_train)
X_test_scaled = scaler.transform(X_test)


# Create model and fit it to the training data.
model = LinearRegression()
model.fit(X_train_scaled, y_train)


# Make predictions.
y_pred = model.predict(X_test_scaled)


# Calculate and print errors.
r2 = r2_score(y_test, y_pred)
print(f"R-squared: {r2:.4f}")


mse = mean_squared_error(y_test, y_pred)
print(f"Mean squared error: {mse:.4f}")


rmse = mse ** 0.5
print(f"Root mean squared error: {rmse:.4f}")

R-squared: 0.5758
Mean squared error: 0.5559
Root mean squared error: 0.7456

Vemos que los resultados son bastante mejores que cuando se utiliza una sola función. Sin embargo, esto plantea la cuestión de si necesitamos todas las funciones. ¿Hay características más relevantes que otras? Elegir las características más relevantes del conjunto de datos se conoce como selección de características.

La selección de características es importante por varias razones.

• Reduce el sobreajuste. Menos características significan menos complejidad, reduciendo el riesgo de sobreajuste.
• Mejora la precisión. Eliminar rasgos irrelevantes o redundantes ayuda al modelo a centrarse en patrones significativos.
• Mejora la interpretabilidad. Facilita la comprensión de los modelos resaltando los factores más importantes.
• Acelera el entrenamiento. Reducir el número de funciones disminuye el tiempo de cálculo y el uso de memoria.

Cuando varias características están muy correlacionadas, son redundantes, lo que significa que esencialmente están dando al modelo la misma información. Esta situación se denomina multicolinealidad. Aunque la multicolinealidad no siempre afecta a la precisión de los modelos predictivos, complica la selección e interpretación de las características, sobre todo en la regresión lineal y modelos afines.

El Factor de Inflación de la Varianza (VIF) es una métrica utilizada para detectar la multicolinealidad entre predictores. Para cada predictor, el VIF se calcula como: 

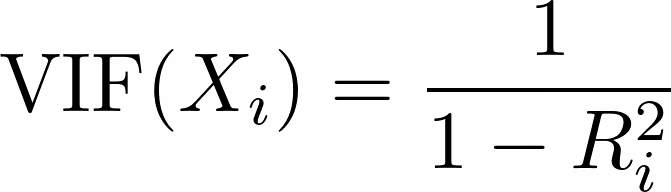
donde ^Ri2 es el valor ^R2 obtenido cuando se hace la regresión del predictor _Xi frente a todos los demás predictores del modelo. Un VIF más alto significa que el predictor está muy correlacionado con otras variables.

• VIF = 1: no hay multicolinealidad (escenario ideal).
• VIF < 5: multicolinealidad de baja a moderada (generalmente aceptable).
• VIF > 5: alta multicolinealidad (considerar la eliminación o combinación de variables correlacionadas).
• VIF > 10: multicolinealidad grave (sugiere claramente redundancia de variables).

# Import libraries.
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
from sklearn.datasets import fetch_california_housing
from statsmodels.stats.outliers_influence import variance_inflation_factor


# Load the dataset.
housing = fetch_california_housing()
X = pd.DataFrame(housing.data, columns=housing.feature_names)


# Compute the correlation matrix.
corr_matrix = X.corr()


# Identify pairs of features with high collinearity (correlation > 0.8 or < -0.8).
high_corr_features = [(col1, col2, corr_matrix.loc[col1, col2])
                     for col1 in corr_matrix.columns
                     for col2 in corr_matrix.columns
                     if col1 != col2 and abs(corr_matrix.loc[col1, col2]) > 0.8]


# Convert to a DataFrame for better visualization.
collinearity_df = pd.DataFrame(high_corr_features, columns=["Feature 1", "Feature 2", "Correlation"])
print("\nHighly Correlated Features:\n", collinearity_df)


# Compute Variance Inflation Factor (VIF) for each feature.
vif_data = pd.DataFrame()
vif_data["Feature"] = X.columns
vif_data["VIF"] = [variance_inflation_factor(X.values, i) for i in range(X.shape[1])]


# Print VIF values.
print("\nVariance Inflation Factor (VIF) for each feature:\n", vif_data)

   Highly Correlated Features:
       Feature 1  Feature 2  Correlation
   0   AveRooms  AveBedrms     0.847621
   1  AveBedrms   AveRooms     0.847621
   2   Latitude  Longitude    -0.924664
   3  Longitude   Latitude    -0.924664
  
   Variance Inflation Factor (VIF) for each feature:
          Feature         VIF
   0      MedInc   11.511140
   1    HouseAge    7.195917
   2    AveRooms   45.993601
   3   AveBedrms   43.590314
   4  Population    2.935745
   5    AveOccup    1.095243
   6    Latitude  559.874071
   7   Longitude  633.711654

Eliminemos AveBedrms del modelo.

# Import libraries.
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.datasets import fetch_california_housing
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error, r2_score


# Load California housing dataset.
housing = fetch_california_housing()


# Create DataFrame and remove "AveBedrms" feature.
X = pd.DataFrame(housing.data, columns=housing.feature_names).drop(columns=["AveBedrms"])
y = housing.target  # Median house value in $100,000s


# Split data into training and testing sets.
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)


# Scale the data (Standardization).
scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train)
X_test_scaled = scaler.transform(X_test)


# Create a linear regression model and train it.
model = LinearRegression()
model.fit(X_train_scaled, y_train)


# Make predictions on the test set.
y_pred = model.predict(X_test_scaled)


# Calculate performance metrics.
r2 = r2_score(y_test, y_pred)
mse = mean_squared_error(y_test, y_pred)
rmse = np.sqrt(mse)
# Print evaluation metrics
print(f"R-squared: {r2:.4f}")
print(f"Mean squared error: {mse:.4f}")
print(f"Root mean squared error: {rmse:.4f}")

R-squared: 0.5823
Mean squared error: 0.5473
Root mean squared error: 0.7398

Los resultados mejoran (marginalmente).

Extraer información del modelo

Construir un modelo de regresión es sólo el primer paso; comprender sus resultados es igualmente importante. Analizando los coeficientes del modelo, podemos determinar qué características tienen un impacto más significativo en las predicciones.

Comprender los coeficientes de regresión

Una vez entrenado un modelo de regresión lineal, se puede acceder a los coeficientes mediante model.coef_. Se puede acceder a la interceptación mediante model.intercept_.

Una vez entrenado un modelo de regresión lineal mediante LinearRegression(), se puede acceder a los coeficientes mediante model.coef_ y se puede acceder al intercepto con model.intercept_.

print("Intercept:", model.intercept_)


coeff_df = pd.DataFrame({"Feature": X.columns, "Coefficient": model.coef_})
print("\nFeature Coefficients:\n", coeff_df)

   Intercept: 2.0719469373788777  

   Feature Coefficients:

         Feature  Coefficient

   0     MedInc     0.725747

   1   HouseAge     0.121519

   2   Latitude    -0.943105

   3  Longitude    -0.900735

Resumir los resultados del modelo

Como Scikit-Learn no proporciona un método incorporado summary() como Statsmodels, podemos extraer y visualizar manualmente la importancia de cada característica mediante coeficientes de regresión. Las características con coeficientes absolutos mayores tienen un mayor impacto en la variable objetivo. Considera el siguiente código.

# Sort dataframe by coefficients.
coef_df_sorted = coef_df.sort_values(by="Coefficient", ascending=False)


# Create plot.
plt.figure(figsize=(8,6))
plt.barh(coef_df["Feature"], coef_df_sorted["Coefficient"], color="blue")
plt.xlabel("Coefficient Value")
plt.ylabel("Feature")
plt.title("Feature Importance (Linear Regression Coefficients)")
plt.show()

Gráfico de la importancia de las características según los valores de los coeficientes

Ahora, vamos a visualizar los residuos y el ajuste de la regresión.

# Compute residuals.
residuals = y_test - y_pred


# Create plots.
plt.figure(figsize=(12,5))


# Plot 1: Residuals Distribution.
plt.subplot(1,2,1)
sns.histplot(residuals, bins=30, kde=True, color="blue")
plt.axvline(x=0, color='red', linestyle='--')
plt.title("Residuals Distribution")
plt.xlabel("Residuals (y_actual - y_predicted)")
plt.ylabel("Frequency")


# Plot 2: Regression Fit (Actual vs Predicted).
plt.subplot(1,2,2)
sns.scatterplot(x=y_test, y=y_pred, alpha=0.5)
plt.plot([min(y_test), max(y_test)], [min(y_test), max(y_test)], color='red', linestyle='--')  # Perfect fit line
plt.title("Regression Fit: Actual vs Predicted")
plt.xlabel("Actual Prices (in $100,000s)")
plt.ylabel("Predicted Prices (in $100,000s)")


# Show plots.
plt.tight_layout()
plt.show()

Gráficos para visualizar los residuos y el ajuste de la regresión

La distribución de los residuos (gráfico de la izquierda) debe estar centrada en torno a cero, lo que indica que los errores están distribuidos aleatoriamente. Si los residuos siguen una distribución normal, el modelo se ajusta bien, pero si hay asimetría o una tendencia, puede sugerir errores sistemáticos. El ajuste de regresión (gráfico de la derecha) compara los valores reales con los previstos, y la línea discontinua roja representa un ajuste perfecto. Si los puntos siguen de cerca la línea, las predicciones son exactas, pero si aparece un patrón (por ejemplo, una curva), puede que la relación no sea realmente lineal. 

Estas visualizaciones ayudan a diagnosticar el exceso o la falta de ajuste, revelan patrones en los residuos que sugieren relaciones perdidas y proporcionan una evaluación clara de la eficacia del modelo.

Aplicaciones en el mundo real

La regresión lineal se utiliza ampliamente en todos los sectores para la predicción y la toma de decisiones. En el sector inmobiliario, estima el precio de la vivienda en función de factores como el tamaño y la ubicación. 

Las ventas y el marketing lo utilizan para prever la demanda y optimizar el presupuesto, mientras que la sanidad lo aplica a la evaluación del riesgo de enfermedad. En finanzas, ayuda a predecir el precio de las acciones y a puntuar los créditos, y en la fabricación, ayuda a controlar la calidad y a predecir los fallos. 

Cuándo utilizar la regresión lineal

• Las características y la variable objetivo tienen una relación lineal.
• La interpretabilidad y la sencillez importan más que los modelos complejos.
• Los datos requieren una ingeniería de características mínima.

Cuándo no utilizar la regresión lineal

• La relación entre el objetivo y las características es compleja y no lineal.
• Los datos están muy correlacionados.
• Los datos contienen valores atípicos que no pueden eliminarse. En este caso, puede que tengas que aplicar transformaciones de datos o utilizar estrategias para mitigar su impacto.

Conclusión

La regresión lineal sigue siendo una de las técnicas más fundamentales y utilizadas en el aprendizaje automático y la modelización estadística. A pesar de su sencillez, es una poderosa herramienta para comprender las relaciones entre variables y hacer predicciones en diversas aplicaciones del mundo real.

Estos son los puntos clave del tutorial:

• Aplicaciones versátiles. La regresión lineal proporciona información valiosa en múltiples sectores y ámbitos problemáticos.
• Interpretable.  A diferencia de los complejos modelos de caja negra, la regresión lineal ofrece interpretaciones claras basadas en coeficientes, por lo que es fácil de interpretar y explicar.
• Selección de características. Seleccionar adecuadamente las características y abordar la multicolinealidad garantiza que los modelos sigan siendo precisos, estables y fiables. 

Para más información sobre la interpolación de cadenas en Python, consulta los recursos de DataCamp.

• Regresión lineal simple: Todo lo que necesitas saber - Tutorial
• Cómo hacer una regresión lineal en R - Tutorial
• Regresión lineal en Excel: Guía completa para principiantes - Tutorial
• Introducción a la Regresión en R - Curso
• Aprendizaje Supervisado con scikit-learn - Curso
• Hoja de trucos de Scikit-Learn: Aprendizaje automático en Python - Hoja de trucos
• Comprender la regresión logística en Python - Tutorial