Regressão linear do Sklearn: Um guia completo com exemplos

A regressão linear é uma técnica fundamental em estatística e machine learning que ajuda a modelar a relação entre as variáveis. Em termos simples, ele nos permite prever um resultado com base em um ou mais fatores de influência. É amplamente aplicado em preços de imóveis, previsão de vendas, avaliação de riscos e muitos outros campos.

Neste tutorial, exploraremos a regressão linear no scikit-learn, abordando como ela funciona, por que é útil e como implementá-la usando o scikit-learn. Ao final, você será capaz de criar e avaliar um modelo de regressão linear para fazer previsões orientadas por dados.

Gráfico de dispersão do preço da casa em relação ao número de cômodos

Regressão linear e machine learning

Além de sua utilidade imediata na determinação dos preços das casas, a regressão linear desempenha um papel importante no machine learning.

• É um modelo básico para a compreensão de técnicas mais avançadas, como regressão logística, redes neurais e máquinas de vetores de suporte.
• O treinamento é rápido, o que o torna ideal para prototipagem rápida.
• Ele também serve como linha de base para comparação. Se os modelos mais avançados não apresentarem desempenho significativamente superior, sua complexidade adicional pode não se justificar.
• Ao contrário de algumas técnicas (como a aprendizagem profunda), ela é facilmente interpretável.
• Ele pode ajudar na seleção de recursos, identificando os preditores mais úteis.

Apesar de sua simplicidade, a regressão linear continua sendo uma ferramenta indispensável no machine learning devido à sua eficiência, interpretabilidade e versatilidade.

Regressão linear e a biblioteca scikit-learn

A biblioteca scikit-learn facilita a implementação da regressão linear. Essa biblioteca tem muitas vantagens.

• Ele tem uma interface consistente. O código necessário para implementar diferentes algoritmos de ML é semelhante.
• O código é simples, com detalhes matemáticos e de implementação complexos extraídos. Por exemplo, para ajustar um modelo nos dados de treinamento, basta usar a linha model.fit(X_train, y_train).
• Ele fornece acesso fácil aos coeficientes do modelo.
• Ele fornece métricas incorporadas para avaliar o desempenho do modelo.
• É fácil integrar a regressão linear (ou qualquer outro algoritmo de ML) com etapas de pré-processamento, como dimensionamento e seleção de recursos, usando o Pipeline.

Se você é novo no scikit-learn, pode conferir nosso curso sobre machine learning com scikit-learn para obter uma introdução prática à biblioteca Python. 

Entendendo a regressão linear

Como vimos, na regressão linear simples, os dados são modelados usando uma "linha de melhor ajuste". A fórmula para essa linha é: 

onde m é a inclinação da linha e b é a interceptação.

A "regressão linear múltipla" generaliza o caso de um preditor para vários preditores (número de quartos, proximidade do oceano, renda média do bairro). A fórmula é generalizada para: 

em que cada _xi é uma variável independente e o _bi correspondente é seu coeficiente. Em três dimensões, a linha é generalizada para um plano. Em dimensões mais altas, o plano se torna um "hiperplano".

Como interpretamos os coeficientes e a interceptação? O intercepto é o valor previsto de y quando todas as variáveis independentes são 0 ou, em outras palavras, é o valor de linha de base da variável dependente quando não há contribuição dos preditores. Cada coeficiente _bi representa a alteração na variável dependente y para uma alteração de uma unidade em _xi, mantendo todas as outras variáveis independentes constantes.

Configuração do ambiente

A instalação do scikit-learn é fácil. Basta usar o comando pip install scikit-learn. Se você quiser instalar uma versão específica, por exemplo, 1.2.2, modifique o comando para incluir a versão: pip install scikit-learn==1.2.2. Se você usa o Anaconda, o scikit-learn já deve estar instalado. Se, por algum motivo, você ainda precisar instalá-lo ao usar a distribuição do Anaconda, use o comando conda install scikit-learn.

Várias bibliotecas são necessárias ou recomendadas quando você usa o scikit-learn. A biblioteca numpy é necessária para armazenar recursos e rótulos. A biblioteca pandas é recomendada para o carregamento, o pré-processamento e a exploração de conjuntos de dados .

Se você estiver usando o scikit-learn, provavelmente já está usando o pandas para a preparação de dados. Para plotar seus resultados, você provavelmente usará matplotlib ou seaborn ou ambos. Qualquer uma dessas bibliotecas pode ser instalada usando o pip install, como no exemplo acima. Você pode até mesmo instalar várias bibliotecas usando um único comando:

pip install scikit-learn numpy pandas matplotlib seaborn.

Implementação da regressão linear no sklearn

Antes de carregarmos o conjunto de dados, vamos importar os suspeitos de sempre.

# Import libraries.
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns

Carregando o conjunto de dados

Vamos usar o conhecido conjunto de dados habitacionais da Califórnia.

# Read in California housing dataset.
from sklearn.datasets import fetch_california_housing


housing = fetch_california_housing()

Preparando os dados

Vamos dividir os dados em conjuntos de treinamento e de teste. Importamos o método train_test_split() de sklearn.model_selection e, em seguida, o invocamos, especificando uma porcentagem do conjunto de testes e um random_state. Também usaremos a regressão linear simples, usando o recurso correspondente ao número médio de quartos.

# Import train_test_split.
from sklearn.model_selection import train_test_split


# Create features X and target y.
X = pd.DataFrame(housing.data, columns=housing.feature_names)[["AveRooms"]]
y = housing.target  # Median house value in $100,000s


# Split the dataset into training (80%) and testing (20%) sets.
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

Agora que dividimos os dados em conjuntos de teste e de treinamento, vamos padronizar os recursos. Esse processo garante que todas as variáveis estejam na mesma escala, o que pode melhorar o desempenho do modelo e a estabilidade numérica.

# Import StandardScaler.
from sklearn.preprocessing import StandardScaler

# Instantiate StandardScaler.
scaler = StandardScaler()

# Fit and transform training data.
X_train_scaled = scaler.fit_transform(X_train)

# Also transform test data.
X_test_scaled = scaler.transform(X_test)

Nesse código, StandardScaler é uma ferramenta de pré-processamento de dados usada para remover a média e dimensionar os recursos para a variância da unidade. Isso ajuda a evitar que determinados recursos dominem o modelo devido a diferenças de escala.

O dimensionador é ajustado nos dados de treinamento usando o métodofit_transform(). Os dados de teste são então transformados separadamente usando o método transform() para garantir que sejam dimensionados usando os mesmos fatores que os dados de treinamento, evitando o vazamento de dados.

Treinamento do modelo de regressão linear

Para criar um modelo de regressão linear, importe LinearRegression() de sklearn.linear_model. Chame-o e atribua-o a uma variável.

# Import LinearRegression.
from sklearn.linear_model import LinearRegression


# Instantiate linear regression model.
model = LinearRegression()

O ajuste do modelo com dados de treinamento é simples.

# Fit the model to the training data.
model.fit(X_train_scaled, y_train)

Fazendo previsões

Agora que treinamos nosso modelo, fazemos previsões no conjunto de teste.

# Make predictions on the testing data.
y_pred = model.predict(X_test_scaled)

Avaliação do desempenho do modelo

Agora que fizemos previsões no conjunto de testes, precisamos saber se elas correspondem à realidade. Há várias métricas disponíveis para avaliar o desempenho de um algoritmo de regressão. Alguns dos mais comuns são o coeficiente de determinação (^R2), o erro quadrático médio (MSE) e a raiz do erro quadrático médio (RMSE).

O coeficiente de determinação, denominado^R2, mede o grau em que um modelo de regressão explica a variabilidade da variável-alvo. Em outras palavras, ele quantifica o quanto da variabilidade na variável-alvo é explicada pelos preditores, o que é conhecido como adequação do ajuste.

Para entender melhor isso, vamos analisar a fórmula:

em que yactual são os valores reais da variável-alvo, ypredicted são os valores previstos pelo modelo e ȳ é a média dos valores reais. Essa fórmula nos ajuda a entender o quanto a variação na variável-alvo é explicada pelo modelo. O denominador representa a variação total nos dados, enquanto o numerador representa a variação não explicada após a aplicação do modelo de regressão. A proporção, portanto, fornece a porcentagem da variação explicada pelo modelo.

Como interpretamos o^R2?

• ^R2 = 1: o modelo explica perfeitamente toda a variação da variável-alvo. 
• ^R2 = 0: o modelo não explica nenhuma das variações; as previsões não são melhores do que simplesmente usar a média. 
• R² < 0: O modelo tem um desempenho pior do que o simples uso da média, indicando um ajuste ruim.

Algumas considerações importantes que você deve ter em mente.

• ^R2 mais alto nem sempre é melhor. Um^R2 alto pode indicar ajuste excessivo, especialmente com modelos complexos. 
• A adição de mais recursos pode aumentar artificialmente o^R2, portanto, um valor mais alto não é necessariamente melhor.
• Para regressão múltipla, use o^R2 ajustado, que leva em conta o número de preditores e evita melhorias enganosas de variáveis desnecessárias.

Avaliar o desempenho do modelo usando o coeficiente de determinação é fácil com o scikit-learn.

# Import metrics.
from sklearn.metrics import mean_squared_error, r2_score


# Calculate and print R^2 score.
r2 = r2_score(y_test, y_pred)
print(f"R-squared: {r2:.4f}")

R-squared: 0.0138

Outras métricas comumente usadas são o erro quadrático médio (MSE) e a raiz do erro quadrático médio (RMSE). Essas métricas medem o quanto as previsões de um modelo se desviam dos valores reais.

O MSE calcula a diferença média ao quadrado entre os valores reais e previstos: 

para o número total de observações n. Como os erros são elevados ao quadrado antes de calcular a média, os erros maiores são mais penalizados do que os menores, o que torna o MSE sensível a valores discrepantes. Um MSE menor indica um melhor ajuste do modelo.

Para resolver esse problema, é usado o RMSE, que é simplesmente a raiz quadrada do MSE. Como o RMSE está nas mesmas unidades que a variável-alvo, ele fornece uma medida mais interpretável de quão longe as previsões estão, em média.

Calcular o MSE e o RMSE é fácil com o scikit-learn.

# Calculate and print MSE.
mse = mean_squared_error(y_test, y_pred)
print(f"Mean squared error: {mse:.4f}")


# Calculate and print RMSE.
rmse = mse ** 0.5
print(f"Root mean squared error: {rmse:.4f}")

Mean squared error: 1.2923
Root mean squared error: 1.1368

Trabalhando com regressão linear múltipla no scikit-learn

Vamos executar novamente o modelo usando todos os nossos recursos disponíveis, não apenas o número médio de quartos. Você espera resultados melhores ou piores?

# Uses all features.
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.datasets import fetch_california_housing
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error, r2_score


# Load data set.
housing = fetch_california_housing()


# Split into X, y.
X = pd.DataFrame(housing.data, columns=housing.feature_names)
y = housing.target  # Median house value in $100,000s
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)


# Scale the data.
scaler = StandardScaler()


X_train_scaled = scaler.fit_transform(X_train)
X_test_scaled = scaler.transform(X_test)


# Create model and fit it to the training data.
model = LinearRegression()
model.fit(X_train_scaled, y_train)


# Make predictions.
y_pred = model.predict(X_test_scaled)


# Calculate and print errors.
r2 = r2_score(y_test, y_pred)
print(f"R-squared: {r2:.4f}")


mse = mean_squared_error(y_test, y_pred)
print(f"Mean squared error: {mse:.4f}")


rmse = mse ** 0.5
print(f"Root mean squared error: {rmse:.4f}")

R-squared: 0.5758
Mean squared error: 0.5559
Root mean squared error: 0.7456

Vemos que os resultados são um pouco melhores do que quando você usa apenas um recurso. No entanto, isso levanta a questão de saber se precisamos de todos os recursos. Alguns recursos são mais relevantes do que outros? A escolha dos recursos mais relevantes do conjunto de dados é conhecida como seleção de recursos.

A seleção de recursos é importante por vários motivos.

• Reduz o ajuste excessivo. Menos recursos significam menos complexidade, reduzindo o risco de ajuste excessivo.
• Melhora a precisão. A remoção de recursos irrelevantes ou redundantes ajuda o modelo a se concentrar em padrões significativos.
• Aumenta a capacidade de interpretação. Torna os modelos mais fáceis de entender, destacando os fatores mais importantes.
• Acelera o treinamento. A redução do número de recursos diminui o tempo de computação e o uso da memória.

Quando vários recursos são altamente correlacionados, eles são redundantes, o que significa que estão basicamente fornecendo ao modelo as mesmas informações. Essa situação é chamada de multicolinearidade. Embora a multicolinearidade nem sempre afete a precisão dos modelos preditivos, ela complica a seleção e a interpretação dos recursos, especialmente na regressão linear e nos modelos relacionados.

O VIF (Variance Inflation Factor, fator de inflação de variância) é uma métrica usada para detectar multicolinearidade entre os preditores. Para cada preditor, o VIF é calculado como: 

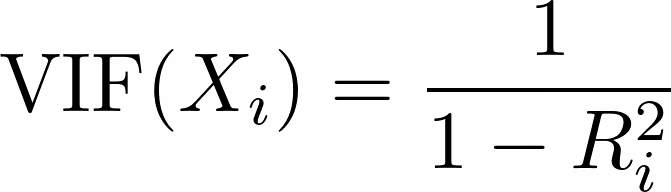
em que ^Ri2 é o valor ^R2 obtido quando o preditor _Xi é regredido em relação a todos os outros preditores no modelo. Um VIF mais alto significa que o preditor está altamente correlacionado com outras variáveis.

• VIF = 1: sem multicolinearidade (cenário ideal).
• VIF < 5: multicolinearidade baixa a moderada (geralmente aceitável).
• VIF > 5: alta multicolinearidade (considere remover ou combinar variáveis correlacionadas).
• VIF > 10: multicolinearidade grave (sugere fortemente redundância de variáveis).

# Import libraries.
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
from sklearn.datasets import fetch_california_housing
from statsmodels.stats.outliers_influence import variance_inflation_factor


# Load the dataset.
housing = fetch_california_housing()
X = pd.DataFrame(housing.data, columns=housing.feature_names)


# Compute the correlation matrix.
corr_matrix = X.corr()


# Identify pairs of features with high collinearity (correlation > 0.8 or < -0.8).
high_corr_features = [(col1, col2, corr_matrix.loc[col1, col2])
                     for col1 in corr_matrix.columns
                     for col2 in corr_matrix.columns
                     if col1 != col2 and abs(corr_matrix.loc[col1, col2]) > 0.8]


# Convert to a DataFrame for better visualization.
collinearity_df = pd.DataFrame(high_corr_features, columns=["Feature 1", "Feature 2", "Correlation"])
print("\nHighly Correlated Features:\n", collinearity_df)


# Compute Variance Inflation Factor (VIF) for each feature.
vif_data = pd.DataFrame()
vif_data["Feature"] = X.columns
vif_data["VIF"] = [variance_inflation_factor(X.values, i) for i in range(X.shape[1])]


# Print VIF values.
print("\nVariance Inflation Factor (VIF) for each feature:\n", vif_data)

   Highly Correlated Features:
       Feature 1  Feature 2  Correlation
   0   AveRooms  AveBedrms     0.847621
   1  AveBedrms   AveRooms     0.847621
   2   Latitude  Longitude    -0.924664
   3  Longitude   Latitude    -0.924664
  
   Variance Inflation Factor (VIF) for each feature:
          Feature         VIF
   0      MedInc   11.511140
   1    HouseAge    7.195917
   2    AveRooms   45.993601
   3   AveBedrms   43.590314
   4  Population    2.935745
   5    AveOccup    1.095243
   6    Latitude  559.874071
   7   Longitude  633.711654

Vamos remover o AveBedrms do modelo.

# Import libraries.
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.datasets import fetch_california_housing
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error, r2_score


# Load California housing dataset.
housing = fetch_california_housing()


# Create DataFrame and remove "AveBedrms" feature.
X = pd.DataFrame(housing.data, columns=housing.feature_names).drop(columns=["AveBedrms"])
y = housing.target  # Median house value in $100,000s


# Split data into training and testing sets.
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)


# Scale the data (Standardization).
scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train)
X_test_scaled = scaler.transform(X_test)


# Create a linear regression model and train it.
model = LinearRegression()
model.fit(X_train_scaled, y_train)


# Make predictions on the test set.
y_pred = model.predict(X_test_scaled)


# Calculate performance metrics.
r2 = r2_score(y_test, y_pred)
mse = mean_squared_error(y_test, y_pred)
rmse = np.sqrt(mse)
# Print evaluation metrics
print(f"R-squared: {r2:.4f}")
print(f"Mean squared error: {mse:.4f}")
print(f"Root mean squared error: {rmse:.4f}")

R-squared: 0.5823
Mean squared error: 0.5473
Root mean squared error: 0.7398

Os resultados são (marginalmente) melhores.

Extração de percepções do modelo

Criar um modelo de regressão é apenas a primeira etapa; compreender seus resultados é igualmente importante. Ao analisar os coeficientes do modelo, podemos determinar quais recursos têm o impacto mais significativo sobre as previsões.

Entendendo os coeficientes de regressão

Depois que um modelo de regressão linear é treinado, os coeficientes podem ser acessados usando model.coef_. Você pode acessar a interceptação usando model.intercept_.

Depois que um modelo de regressão linear é treinado usando LinearRegression(), os coeficientes podem ser acessados usando model.coef_ e a interceptação pode ser acessada usando model.intercept_.

print("Intercept:", model.intercept_)


coeff_df = pd.DataFrame({"Feature": X.columns, "Coefficient": model.coef_})
print("\nFeature Coefficients:\n", coeff_df)

   Intercept: 2.0719469373788777  

   Feature Coefficients:

         Feature  Coefficient

   0     MedInc     0.725747

   1   HouseAge     0.121519

   2   Latitude    -0.943105

   3  Longitude    -0.900735

Resumo dos resultados do modelo

Como o Scikit-Learn não oferece um método summary() integrado como o Statsmodels, podemos extrair e visualizar manualmente a importância de cada recurso usando os coeficientes de regressão. Os recursos com coeficientes absolutos maiores têm um impacto mais forte sobre a variável de destino. Considere o código a seguir.

# Sort dataframe by coefficients.
coef_df_sorted = coef_df.sort_values(by="Coefficient", ascending=False)


# Create plot.
plt.figure(figsize=(8,6))
plt.barh(coef_df["Feature"], coef_df_sorted["Coefficient"], color="blue")
plt.xlabel("Coefficient Value")
plt.ylabel("Feature")
plt.title("Feature Importance (Linear Regression Coefficients)")
plt.show()

Gráfico da importância do recurso com base nos valores do coeficiente

Agora, vamos visualizar os resíduos e o ajuste da regressão.

# Compute residuals.
residuals = y_test - y_pred


# Create plots.
plt.figure(figsize=(12,5))


# Plot 1: Residuals Distribution.
plt.subplot(1,2,1)
sns.histplot(residuals, bins=30, kde=True, color="blue")
plt.axvline(x=0, color='red', linestyle='--')
plt.title("Residuals Distribution")
plt.xlabel("Residuals (y_actual - y_predicted)")
plt.ylabel("Frequency")


# Plot 2: Regression Fit (Actual vs Predicted).
plt.subplot(1,2,2)
sns.scatterplot(x=y_test, y=y_pred, alpha=0.5)
plt.plot([min(y_test), max(y_test)], [min(y_test), max(y_test)], color='red', linestyle='--')  # Perfect fit line
plt.title("Regression Fit: Actual vs Predicted")
plt.xlabel("Actual Prices (in $100,000s)")
plt.ylabel("Predicted Prices (in $100,000s)")


# Show plots.
plt.tight_layout()
plt.show()

Gráficos para visualizar resíduos e ajuste de regressão

A distribuição de resíduos (gráfico à esquerda) deve ser centralizada em zero, indicando que os erros são distribuídos aleatoriamente. Se os resíduos seguirem uma distribuição normal, o modelo se ajusta bem, mas se houver distorção ou tendência, isso pode sugerir erros sistemáticos. O ajuste de regressão (gráfico à direita) compara os valores reais com os valores previstos, com a linha tracejada vermelha representando um ajuste perfeito. Se os pontos seguirem a linha de perto, as previsões serão precisas, mas se aparecer um padrão (por exemplo, uma curva), a relação pode não ser realmente linear. 

Essas visualizações ajudam a diagnosticar o excesso ou a falta de ajuste, revelam padrões nos resíduos que sugerem relações ausentes e fornecem uma avaliação clara da eficácia do modelo.

Aplicativos do mundo real

A regressão linear é amplamente usada em todos os setores para previsão e tomada de decisões. No setor imobiliário, ele estima os preços das casas com base em fatores como tamanho e localização. 

O setor de vendas e marketing o utiliza para previsão de demanda e otimização de orçamento, enquanto o setor de saúde o aplica à avaliação de risco de doenças. Em finanças, ele ajuda na previsão do preço das ações e na pontuação de crédito e, na fabricação, ajuda no controle de qualidade e na previsão de falhas. 

Quando usar a regressão linear

• Os recursos e a variável-alvo têm uma relação linear.
• A interpretabilidade e a simplicidade são mais importantes do que a modelagem complexa.
• Os dados exigem um mínimo de engenharia de recursos.

Quando não usar a regressão linear

• A relação entre o alvo e os recursos é complexa e não linear.
• Os dados são altamente correlacionados.
• Os dados contêm valores discrepantes que não podem ser removidos. Nesse caso, talvez você precise aplicar transformações de dados ou usar estratégias para atenuar o impacto.

Conclusão

A regressão linear continua sendo uma das técnicas mais fundamentais e amplamente usadas em machine learning e modelagem estatística. Apesar de sua simplicidade, é uma ferramenta poderosa para entender as relações entre variáveis e fazer previsões em várias aplicações do mundo real.

Aqui estão as principais conclusões do tutorial:

• Aplicações versáteis. A regressão linear oferece percepções valiosas em vários setores e domínios de problemas.
• Interpretável.  Ao contrário dos modelos complexos de caixa preta, a regressão linear oferece interpretações claras baseadas em coeficientes, o que facilita a interpretação e a explicação.
• Seleção de recursos. A seleção adequada de recursos e o tratamento da multicolinearidade garantem que os modelos permaneçam precisos, estáveis e confiáveis. 

Para obter mais informações sobre a interpolação de strings do Python, consulte os recursos do DataCamp.

• Regressão linear simples: Tudo o que você precisa saber - Tutorial
• Como fazer regressão linear no R - Tutorial
• Regressão linear no Excel: Um guia abrangente para iniciantes - Tutorial
• Introdução à regressão em R - Curso
• Aprendizagem supervisionada com o scikit-learn - Curso
• Folha de dicas do Scikit-Learn: Python Machine Learning - Folha de consulta
• Entendendo a regressão logística em Python - Tutorial