Régression linéaire Sklearnar : Un guide complet avec des exemples

La régression linéaire est une technique fondamentale en statistique et en apprentissage automatique qui permet de modéliser la relation entre les variables. En termes simples, elle nous permet de prédire un résultat sur la base d'un ou de plusieurs facteurs d'influence. Il est largement appliqué dans la fixation des prix de l'immobilier, la prévision des ventes, l'évaluation des risques et bien d'autres domaines.

Dans ce tutoriel, nous allons explorer la régression linéaire dans scikit-learn. Nous verrons comment elle fonctionne, pourquoi elle est utile et comment l'implémenter en utilisant scikit-learn. À la fin du cours, vous serez en mesure de construire et d'évaluer un modèle de régression linéaire pour faire des prédictions basées sur des données.

Diagramme de dispersion du prix du logement en fonction du nombre de pièces

Régression linéaire et apprentissage automatique

Au-delà de son utilité immédiate pour déterminer les prix des logements, la régression linéaire joue un rôle important dans l'apprentissage automatique.

• Il s'agit d'un modèle fondamental pour comprendre des techniques plus avancées telles que la régression logistique, les réseaux neuronaux et les machines à vecteurs de support.
• Il est rapide à former, ce qui le rend idéal pour le prototypage rapide.
• Il sert également de base de comparaison. Si les modèles plus avancés ne sont pas nettement plus performants, leur complexité accrue n'est peut-être pas justifiée.
• Contrairement à certaines techniques (telles que l'apprentissage profond), elle est facilement interprétable.
• Il peut aider à la sélection des caractéristiques, en identifiant les prédicteurs les plus utiles.

Malgré sa simplicité, la régression linéaire reste un outil indispensable dans l'apprentissage automatique en raison de son efficacité, de sa facilité d'interprétation et de sa polyvalence.

Régression linéaire et bibliothèque scikit-learn

La bibliothèque scikit-learn facilite la mise en œuvre de la régression linéaire. Cette bibliothèque présente de nombreux avantages.

• L'interface est cohérente. Le code nécessaire à la mise en œuvre des différents algorithmes de ML est similaire.
• Le code est simple, les mathématiques complexes et les détails de mise en œuvre sont éliminés. Par exemple, pour ajuster un modèle sur des données d'apprentissage, il suffit d'utiliser la ligne model.fit(X_train, y_train).
• Il permet d'accéder facilement aux coefficients du modèle.
• Il fournit des mesures intégrées pour évaluer la performance du modèle.
• Il est facile d'intégrer la régression linéaire (ou tout autre algorithme de ML) aux étapes de prétraitement, telles que la mise à l'échelle et la sélection des caractéristiques, à l'aide de Pipeline.

Si vous ne connaissez pas scikit-learn, vous pouvez consulter notre cours sur l'apprentissage automatique avec scikit-learn pour obtenir une introduction pratique à la bibliothèque Python. 

Comprendre la régression linéaire

Comme nous l'avons vu, dans la régression linéaire simple, les données sont modélisées à l'aide d'une "ligne de meilleur ajustement". La formule pour cette ligne est la suivante : 

où m est la pente de la droite et b l'ordonnée à l'origine.

La "régression linéaire multiple" généralise le cas d'un prédicteur à plusieurs prédicteurs (nombre de chambres, proximité de l'océan, revenu médian du quartier). La formule est généralisée : 

où chaque _xi est une variable indépendante et le _bi correspondant est son coefficient. En trois dimensions, la ligne est généralisée à un plan. Dans les dimensions supérieures, le plan devient un "hyperplan".

Comment interpréter les coefficients et l'ordonnée à l'origine ? L'ordonnée à l'origine est la valeur prédite de y lorsque toutes les variables indépendantes sont égales à 0 ou, en d'autres termes, la valeur de base de la variable dépendante lorsqu'il n'y a pas de contribution des variables prédictives. Chaque coefficient _bi représente la variation de la variable dépendante y pour une variation d'une unité de _xi, toutes les autres variables indépendantes restant constantes.

Mise en place de l'environnement

L'installation de scikit-learn est facile. Il suffit d'utiliser la commande pip install scikit-learn. Si vous souhaitez installer une version spécifique, par exemple 1.2.2, modifiez la commande pour inclure la version : pip install scikit-learn==1.2.2. Si vous utilisez Anaconda, scikit-learn devrait déjà être installé. Si, pour une raison quelconque, vous devez encore l'installer lorsque vous utilisez la distribution Anaconda, utilisez la commande conda install scikit-learn.

Plusieurs bibliothèques sont nécessaires ou recommandées lorsque vous utilisez scikit-learn. La bibliothèque numpy est nécessaire pour stocker les caractéristiques et les étiquettes. La bibliothèque pandas est recommandée pour le chargement, le prétraitement et l'exploration des ensembles de données .

Si vous utilisez scikit-learn, vous utilisez probablement déjà pandas pour la préparation de vos données. Pour tracer vos résultats, vous utiliserez probablement matplotlib ou seaborn ou les deux. Toutes ces bibliothèques peuvent être installées à l'aide de pip install, comme dans l'exemple ci-dessus. Vous pouvez même installer plusieurs bibliothèques à l'aide d'une seule commande :

pip install scikit-learn numpy pandas matplotlib seaborn.

Implémentation de la régression linéaire dans sklearn

Avant de charger l'ensemble de données, importons les suspects habituels.

# Import libraries.
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns

Chargement du jeu de données

Prenons l'exemple de la célèbre base de données californienne sur le logement.

# Read in California housing dataset.
from sklearn.datasets import fetch_california_housing


housing = fetch_california_housing()

Préparation des données

Divisons les données en deux ensembles, l'un pour la formation et l'autre pour les tests. Nous importons la méthode train_test_split() à partir de sklearn.model_selection, puis nous l'invoquons en spécifiant un pourcentage de l'ensemble de test et une adresserandom_state. Nous utiliserons également une régression linéaire simple, en utilisant la caractéristique correspondant au nombre moyen de pièces.

# Import train_test_split.
from sklearn.model_selection import train_test_split


# Create features X and target y.
X = pd.DataFrame(housing.data, columns=housing.feature_names)[["AveRooms"]]
y = housing.target  # Median house value in $100,000s


# Split the dataset into training (80%) and testing (20%) sets.
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

Maintenant que nous avons divisé les données en ensembles de test et de formation, normalisons les caractéristiques. Ce processus garantit que toutes les variables sont à la même échelle, ce qui peut améliorer les performances du modèle et la stabilité numérique.

# Import StandardScaler.
from sklearn.preprocessing import StandardScaler

# Instantiate StandardScaler.
scaler = StandardScaler()

# Fit and transform training data.
X_train_scaled = scaler.fit_transform(X_train)

# Also transform test data.
X_test_scaled = scaler.transform(X_test)

Dans ce code, StandardScaler est un outil de prétraitement des données utilisé pour supprimer la moyenne et mettre les caractéristiques à l'échelle de la variance unitaire. Cela permet d'éviter que certaines caractéristiques ne dominent le modèle en raison de différences d'échelle.

L'échelle est ajustée sur les données d'apprentissage à l'aide de la méthodefit_transform(). Les données de test sont ensuite transformées séparément à l'aide de la méthode transform() afin de s'assurer qu'elles sont mises à l'échelle en utilisant les mêmes facteurs que les données d'apprentissage, ce qui permet d'éviter les fuites de données.

Entraînement du modèle de régression linéaire

Pour créer un modèle de régression linéaire, importez LinearRegression() de sklearn.linear_model. Invoquez-le et affectez-le à une variable.

# Import LinearRegression.
from sklearn.linear_model import LinearRegression


# Instantiate linear regression model.
model = LinearRegression()

L'ajustement du modèle avec les données d'apprentissage est simple.

# Fit the model to the training data.
model.fit(X_train_scaled, y_train)

Faire des prévisions

Maintenant que nous avons entraîné notre modèle, nous faisons des prédictions sur l'ensemble de test.

# Make predictions on the testing data.
y_pred = model.predict(X_test_scaled)

Évaluation de la performance du modèle

Maintenant que nous avons fait des prédictions sur l'ensemble de tests, nous devons savoir dans quelle mesure elles correspondent à la réalité. Il existe plusieurs mesures permettant d'évaluer les performances d'un algorithme de régression. Les plus courants sont le coefficient de détermination (^R2), l'erreur quadratique moyenne (MSE) et l'erreur quadratique moyenne racine (RMSE).

Le coefficient de détermination, noté^R2, mesure à quel point un modèle de régression explique la variabilité de la variable cible. En d'autres termes, il quantifie la part de la variabilité de la variable cible qui est expliquée par les prédicteurs, ce que l'on appelle la qualité de l'ajustement.

Pour mieux comprendre, examinons la formule :

où yactual est la valeur réelle de la variable cible, ypredicted est la valeur prédite par le modèle et ȳ est la moyenne des valeurs réelles. Cette formule nous aide à comprendre quelle variance de la variable cible est expliquée par le modèle. Le dénominateur représente la variance totale des données, tandis que le numérateur représente la variance inexpliquée après application du modèle de régression. Le ratio donne donc le pourcentage de variance expliquée par le modèle.

Comment interpréter^R2?

• ^R2 = 1 : le modèle explique parfaitement toute la variance de la variable cible. 
• ^R2 = 0 : le modèle n'explique aucune partie de la variance ; les prédictions ne sont pas meilleures que l'utilisation de la moyenne. 
• ^R2 < 0 : Le modèle est moins performant que la simple utilisation de la moyenne, ce qui indique une mauvaise adaptation.

Quelques considérations clés à garder à l'esprit.

• Une^R2 plus élevée n'est pas toujours meilleure. Un^R2 élevé peut indiquer un surajustement, en particulier avec des modèles complexes. 
• L'ajout de fonctionnalités peut augmenter artificiellement la valeur^R2, de sorte qu'une valeur plus élevée n'est pas nécessairement meilleure.
• Pour la régression multiple, utilisez le^R2 ajusté, qui tient compte du nombre de prédicteurs et évite les améliorations trompeuses dues à des variables inutiles.

L'évaluation des performances d'un modèle à l'aide du coefficient de détermination est facile à réaliser avec scikit-learn.

# Import metrics.
from sklearn.metrics import mean_squared_error, r2_score


# Calculate and print R^2 score.
r2 = r2_score(y_test, y_pred)
print(f"R-squared: {r2:.4f}")

R-squared: 0.0138

D'autres mesures couramment utilisées sont l'erreur quadratique moyenne (MSE) et l'erreur quadratique moyenne racine (RMSE). Ces paramètres mesurent l'écart entre les prédictions d'un modèle et les valeurs réelles.

L'EQM calcule la différence moyenne au carré entre les valeurs réelles et les valeurs prédites : 

pour le nombre total d'observations n. Étant donné que les erreurs sont élevées au carré avant de calculer la moyenne, les erreurs plus importantes sont plus fortement pénalisées que les plus petites, ce qui rend l'EQM sensible aux valeurs aberrantes. Une EQM plus faible indique une meilleure adéquation du modèle.

Pour résoudre ce problème, on utilise la RMSE, qui est simplement la racine carrée de la MSE. La RMSE étant exprimée dans les mêmes unités que la variable cible, elle fournit une mesure plus facile à interpréter de l'écart moyen entre les prédictions et la réalité.

Le calcul de l'EQM et de l'EQM est facile avec scikit-learn.

# Calculate and print MSE.
mse = mean_squared_error(y_test, y_pred)
print(f"Mean squared error: {mse:.4f}")


# Calculate and print RMSE.
rmse = mse ** 0.5
print(f"Root mean squared error: {rmse:.4f}")

Mean squared error: 1.2923
Root mean squared error: 1.1368

Travailler avec la régression linéaire multiple dans scikit-learn

Ré-exécutons le modèle en utilisant toutes les caractéristiques disponibles, et pas seulement le nombre moyen de chambres. Vous attendez-vous à des résultats meilleurs ou moins bons ?

# Uses all features.
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.datasets import fetch_california_housing
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error, r2_score


# Load data set.
housing = fetch_california_housing()


# Split into X, y.
X = pd.DataFrame(housing.data, columns=housing.feature_names)
y = housing.target  # Median house value in $100,000s
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)


# Scale the data.
scaler = StandardScaler()


X_train_scaled = scaler.fit_transform(X_train)
X_test_scaled = scaler.transform(X_test)


# Create model and fit it to the training data.
model = LinearRegression()
model.fit(X_train_scaled, y_train)


# Make predictions.
y_pred = model.predict(X_test_scaled)


# Calculate and print errors.
r2 = r2_score(y_test, y_pred)
print(f"R-squared: {r2:.4f}")


mse = mean_squared_error(y_test, y_pred)
print(f"Mean squared error: {mse:.4f}")


rmse = mse ** 0.5
print(f"Root mean squared error: {rmse:.4f}")

R-squared: 0.5758
Mean squared error: 0.5559
Root mean squared error: 0.7456

Nous constatons que les résultats sont nettement meilleurs que lorsqu'on n'utilise qu'une seule caractéristique. Toutefois, cela soulève la question de savoir si nous avons besoin de toutes les fonctionnalités. Certaines caractéristiques sont-elles plus pertinentes que d'autres ? Le choix des caractéristiques les plus pertinentes de l'ensemble de données est connu sous le nom de sélection des caractéristiques.

La sélection des caractéristiques est importante pour un certain nombre de raisons.

• Réduit le surajustement. Moins de caractéristiques signifie moins de complexité, ce qui réduit le risque de surajustement.
• Améliore la précision. La suppression des caractéristiques non pertinentes ou redondantes aide le modèle à se concentrer sur les modèles significatifs.
• Améliore l'interprétabilité. Facilite la compréhension des modèles en mettant en évidence les facteurs les plus importants.
• Accélère la formation. La réduction du nombre de caractéristiques diminue le temps de calcul et l'utilisation de la mémoire.

Lorsque plusieurs caractéristiques sont fortement corrélées, elles sont redondantes, ce qui signifie qu'elles fournissent essentiellement les mêmes informations au modèle. Cette situation est appelée multicollinéarité. Bien que la multicollinéarité n'ait pas toujours un impact sur la précision des modèles prédictifs, elle complique la sélection et l'interprétation des caractéristiques, en particulier dans la régression linéaire et les modèles apparentés.

Le facteur d'inflation de la variance (VIF) est une mesure utilisée pour détecter la multicolinéarité entre les prédicteurs. Pour chaque prédicteur, le VIF est calculé comme suit : 

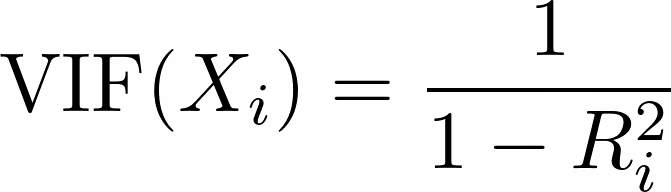
où ^Ri2 est la valeur ^R2 obtenue lorsque le prédicteur _Xi est régressé par rapport à tous les autres prédicteurs du modèle. Un VIF élevé signifie que le prédicteur est fortement corrélé avec d'autres variables.

• VIF = 1 : pas de multicolinéarité (scénario idéal).
• VIF < 5 : multicolinéarité faible à modérée (généralement acceptable).
• VIF > 5 : forte multicolinéarité (envisagez de supprimer ou de combiner les variables corrélées).
• VIF > 10 : multicolinéarité sévère (suggère fortement une redondance des variables).

# Import libraries.
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
from sklearn.datasets import fetch_california_housing
from statsmodels.stats.outliers_influence import variance_inflation_factor


# Load the dataset.
housing = fetch_california_housing()
X = pd.DataFrame(housing.data, columns=housing.feature_names)


# Compute the correlation matrix.
corr_matrix = X.corr()


# Identify pairs of features with high collinearity (correlation > 0.8 or < -0.8).
high_corr_features = [(col1, col2, corr_matrix.loc[col1, col2])
                     for col1 in corr_matrix.columns
                     for col2 in corr_matrix.columns
                     if col1 != col2 and abs(corr_matrix.loc[col1, col2]) > 0.8]


# Convert to a DataFrame for better visualization.
collinearity_df = pd.DataFrame(high_corr_features, columns=["Feature 1", "Feature 2", "Correlation"])
print("\nHighly Correlated Features:\n", collinearity_df)


# Compute Variance Inflation Factor (VIF) for each feature.
vif_data = pd.DataFrame()
vif_data["Feature"] = X.columns
vif_data["VIF"] = [variance_inflation_factor(X.values, i) for i in range(X.shape[1])]


# Print VIF values.
print("\nVariance Inflation Factor (VIF) for each feature:\n", vif_data)

   Highly Correlated Features:
       Feature 1  Feature 2  Correlation
   0   AveRooms  AveBedrms     0.847621
   1  AveBedrms   AveRooms     0.847621
   2   Latitude  Longitude    -0.924664
   3  Longitude   Latitude    -0.924664
  
   Variance Inflation Factor (VIF) for each feature:
          Feature         VIF
   0      MedInc   11.511140
   1    HouseAge    7.195917
   2    AveRooms   45.993601
   3   AveBedrms   43.590314
   4  Population    2.935745
   5    AveOccup    1.095243
   6    Latitude  559.874071
   7   Longitude  633.711654

Supprimons AveBedrms du modèle.

# Import libraries.
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.datasets import fetch_california_housing
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error, r2_score


# Load California housing dataset.
housing = fetch_california_housing()


# Create DataFrame and remove "AveBedrms" feature.
X = pd.DataFrame(housing.data, columns=housing.feature_names).drop(columns=["AveBedrms"])
y = housing.target  # Median house value in $100,000s


# Split data into training and testing sets.
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)


# Scale the data (Standardization).
scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train)
X_test_scaled = scaler.transform(X_test)


# Create a linear regression model and train it.
model = LinearRegression()
model.fit(X_train_scaled, y_train)


# Make predictions on the test set.
y_pred = model.predict(X_test_scaled)


# Calculate performance metrics.
r2 = r2_score(y_test, y_pred)
mse = mean_squared_error(y_test, y_pred)
rmse = np.sqrt(mse)
# Print evaluation metrics
print(f"R-squared: {r2:.4f}")
print(f"Mean squared error: {mse:.4f}")
print(f"Root mean squared error: {rmse:.4f}")

R-squared: 0.5823
Mean squared error: 0.5473
Root mean squared error: 0.7398

Les résultats sont (légèrement) améliorés.

Extraire des informations sur les modèles

L'élaboration d'un modèle de régression n'est que la première étape ; la compréhension de ses résultats est tout aussi importante. En analysant les coefficients du modèle, nous pouvons déterminer quelles caractéristiques ont l'impact le plus significatif sur les prédictions.

Comprendre les coefficients de régression

Une fois qu'un modèle de régression linéaire est formé, les coefficients peuvent être consultés à l'aide de model.coef_. Vous pouvez accéder à l'interception en utilisant model.intercept_.

Une fois qu'un modèle de régression linéaire est formé à l'aide de LinearRegression(), les coefficients peuvent être accédés à l'aide de model.coef_ et l'ordonnée à l'origine peut être consultée à l'aide de model.intercept_.

print("Intercept:", model.intercept_)


coeff_df = pd.DataFrame({"Feature": X.columns, "Coefficient": model.coef_})
print("\nFeature Coefficients:\n", coeff_df)

   Intercept: 2.0719469373788777  

   Feature Coefficients:

         Feature  Coefficient

   0     MedInc     0.725747

   1   HouseAge     0.121519

   2   Latitude    -0.943105

   3  Longitude    -0.900735

Synthèse des résultats du modèle

Comme Scikit-Learn ne fournit pas de méthode intégrée summary() comme Statsmodels, nous pouvons extraire et visualiser manuellement l'importance de chaque caractéristique à l'aide de coefficients de régression. Les caractéristiques ayant des coefficients absolus plus élevés ont un impact plus important sur la variable cible. Considérez le code suivant.

# Sort dataframe by coefficients.
coef_df_sorted = coef_df.sort_values(by="Coefficient", ascending=False)


# Create plot.
plt.figure(figsize=(8,6))
plt.barh(coef_df["Feature"], coef_df_sorted["Coefficient"], color="blue")
plt.xlabel("Coefficient Value")
plt.ylabel("Feature")
plt.title("Feature Importance (Linear Regression Coefficients)")
plt.show()

Graphique de l'importance des caractéristiques en fonction des valeurs des coefficients

Visualisons maintenant les résidus et l'ajustement de la régression.

# Compute residuals.
residuals = y_test - y_pred


# Create plots.
plt.figure(figsize=(12,5))


# Plot 1: Residuals Distribution.
plt.subplot(1,2,1)
sns.histplot(residuals, bins=30, kde=True, color="blue")
plt.axvline(x=0, color='red', linestyle='--')
plt.title("Residuals Distribution")
plt.xlabel("Residuals (y_actual - y_predicted)")
plt.ylabel("Frequency")


# Plot 2: Regression Fit (Actual vs Predicted).
plt.subplot(1,2,2)
sns.scatterplot(x=y_test, y=y_pred, alpha=0.5)
plt.plot([min(y_test), max(y_test)], [min(y_test), max(y_test)], color='red', linestyle='--')  # Perfect fit line
plt.title("Regression Fit: Actual vs Predicted")
plt.xlabel("Actual Prices (in $100,000s)")
plt.ylabel("Predicted Prices (in $100,000s)")


# Show plots.
plt.tight_layout()
plt.show()

Graphiques pour visualiser les résidus et l'ajustement de la régression

La distribution des résidus (graphique de gauche) doit être centrée autour de zéro, ce qui indique que les erreurs sont distribuées de manière aléatoire. Si les résidus suivent une distribution normale, le modèle s'ajuste bien, mais s'il y a une asymétrie ou une tendance, cela peut suggérer des erreurs systématiques. L'ajustement de la régression (graphique de droite) compare les valeurs réelles aux valeurs prédites, la ligne pointillée rouge représentant un ajustement parfait. Si les points suivent de près la ligne, les prédictions sont exactes, mais si un schéma (par exemple une courbe) apparaît, la relation n'est peut-être pas vraiment linéaire. 

Ces visualisations permettent de diagnostiquer un surajustement ou un sous-ajustement, de révéler des schémas dans les résidus qui suggèrent des relations manquantes et de fournir une évaluation claire de l'efficacité du modèle.

Applications dans le monde réel

La régression linéaire est largement utilisée dans tous les secteurs d'activité pour la prédiction et la prise de décision. Dans le domaine de l'immobilier, il s'agit d'estimer le prix des maisons en fonction de facteurs tels que la taille et l'emplacement. 

Les ventes et le marketing l'utilisent pour la prévision de la demande et l'optimisation du budget, tandis que les soins de santé l'appliquent à l'évaluation des risques de maladie. Dans le domaine de la finance, elle permet de prédire le cours des actions et d'évaluer le crédit, et dans le domaine de la fabrication, elle contribue au contrôle de la qualité et à la prédiction des défaillances. 

Quand utiliser la régression linéaire ?

• Les caractéristiques et la variable cible ont une relation linéaire.
• L'interprétabilité et la simplicité sont plus importantes que la complexité de la modélisation.
• Les données nécessitent un minimum d'ingénierie.

Quand ne pas utiliser la régression linéaire

• La relation entre la cible et les caractéristiques est complexe et non linéaire.
• Les données sont fortement corrélées.
• Les données contiennent des valeurs aberrantes qui ne peuvent être supprimées. Dans ce cas, vous devrez peut-être appliquer des transformations de données ou utiliser des stratégies pour atténuer leur impact.

Conclusion

La régression linéaire reste l'une des techniques les plus fondamentales et les plus largement utilisées dans l'apprentissage automatique et la modélisation statistique. Malgré sa simplicité, il s'agit d'un outil puissant pour comprendre les relations entre les variables et faire des prédictions dans diverses applications du monde réel.

Voici les principaux points à retenir de ce tutoriel :

• Applications polyvalentes. La régression linéaire fournit des informations précieuses dans de nombreux secteurs d'activité et domaines problématiques.
• Interprétable.  Contrairement aux modèles complexes de type "boîte noire", la régression linéaire offre des interprétations claires basées sur les coefficients, ce qui la rend facile à interpréter et à expliquer.
• Sélection des caractéristiques. En sélectionnant correctement les caractéristiques et en tenant compte de la multicolinéarité, vous vous assurez que les modèles restent précis, stables et fiables. 

Pour plus d'informations sur l'interpolation de chaînes de caractères en Python, consultez les ressources de DataCamp.

• Régression linéaire simple : Tout ce que vous devez savoir - Tutoriel
• Comment faire une régression linéaire en R - Tutoriel
• Régression linéaire dans Excel : Un guide complet pour les débutants - Tutoriel
• Introduction à la régression en R - Cours
• Apprentissage supervisé avec scikit-learn - Cours
• Scikit-Learn Cheat Sheet : Python Machine Learning - Aide-mémoire
• Comprendre la régression logistique en Python - Tutoriel